用于光纤传感的可调半软阈值小波去噪算法

邵向鑫,王有朋,张笑鸣,于 鑫,江 虹

(长春工业大学电气与电子工程学院,吉林 长春 130012)

1 引 言

对于大容量FBG传感网络测量系统来说,在采集光纤光栅传感信号的过程中通常会伴随噪声干扰,特别是光路连接处和闲置的尾端等光纤端面产生的固有反射而引起FBG反射光产生的干涉噪声,另外解调系统固有的电子学噪声也会为光纤光栅信号的解调带来不利影响,如何最大限度的去除噪声,提高波长分辨率,保持解调信号的精确性和稳定性至关重要[1-4]。经常用到的去噪方法有很多种,比如:典型的盲源分离法、独立分量分析方法,但由于这些去噪方法在变换后的熵也相应的增加,严重影响了信号本身具有的稳定特性,而由于小波阈值去噪后重构的熵值较低,本文决定采用小波阈值的方法进行去噪。

Donoho教授于1995年提出非常著名的软硬阈值去噪法[5-9],其优点主要表现为易于实现,运算简单,且变换后能够降低熵值,但是在实践应用中该方法仍然存在不足和缺陷。对于硬阈值函数,为了保证其与真实小波系数的精确度,牺牲函数的连续性而诱发震荡,学术界将此现象称之为伪吉布斯效应。而软函数连续性虽然优于硬函数,但是用其处理含噪信号的本质是增大了门限值,这会使处理前后小波系数间产生恒定的门限值误差,降低原始信号的还原度。

虽然在文献[10]～[14]中,王蓓、栗明等构造的阈值函数在整个小波域上是连续的,但是在与真实小波系数的逼近程度上仍然不准确。本文基于传统阈值函数基础上提出改进的小波阈值函数,该函数介于两种传统函数之间,凭借半软阈值因子β来减小与真实小波系数之间的恒定误差,而调节因子μ能够实现函数向软、硬阈值函数的转变,相比于软、硬阈值函数,含噪信号利用本文提出的新阈值函数处理后,能够获得明显改善。

2 小波阈值去噪的过程及阈值函数

2.1 小波阈值去噪的过程

假设含噪信号的表达式如下:

s(t)=f(t)+n(t)

(1)

对s(t)作小波变换,则:

ωs(j,k)=ωf(j,k)+ωn(j,k),j=0,1,…,J,k=0,1,…,N

(2)

式中,s(t)、f(t)和n(t)分别代表含噪信号、初始无噪信号和噪声信号。其中n(t)可被视为方差σ2的高斯白噪声,满足正态分布N(0,σ2)规律,ωj,k对应信号在第j层下的小波系数；J和N分别表示最大的分解层数以及信号长度。

一般地,有用信号f(t)具有连续性,这种特性主要表现在空间和时域上。相比较而言n(t)却不具有连续性。学术界认为噪声生成小波系数的模值比原信号生成的模值小,将其同阈值对比,如果模值大于阈值,则认为是原始信号产生的小波系数,可采取保留操作；如果前者小于后者,则视为噪声产生的小波系数,将其默认为0并摒弃,考虑到这一点,要求实际去噪过程中必须明确阈值范围,防止阈值选取过大或过小给去噪效果的精确性带来不利影响,阈值处理后将进入重构环节,通常该环节又被叫做小波逆变换。整个过程流程具体见图1所示。

图1 小波阈值去噪原理

2.2 阈值函数

本文提到的阈值函数指的是Donoho教授提出的软、硬阈值函数,硬阈值函数的算法原理是:将其中比阈值高的小波系数ωj,k保留下来,而低于阈值的则视为0,函数的表达式以及图像具体如下所示:

(3)

从图2中能够看出:硬阈值函数±λ处并不具有连续性,导致信号重构过程中产生震荡,通常将这种现象叫做伪吉布斯效应。

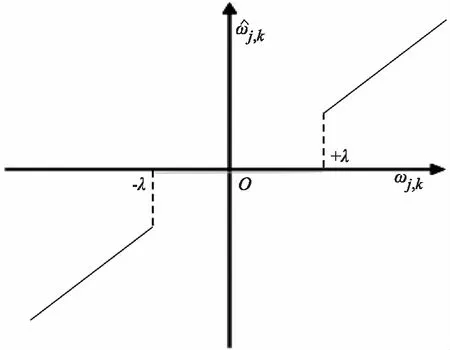
图2 硬阈值函数示意图

软阈值函数算法原理是:将模值比阈值高的ωj,k按照阈值缩减,可有效解决函数不连续的问题,但这种解决办法会带来恒定偏差。函数的表达式以及图像具体如下所示:

(4)

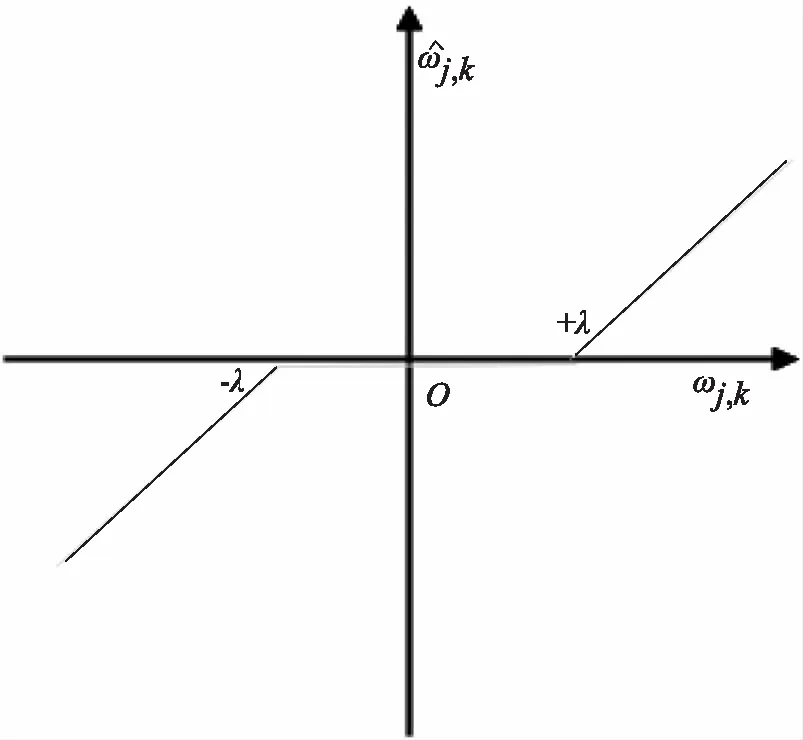
图3 软阈值函数示意图

3 可调节半软阈值函数的构建

3.1 算法实现

针对两种传统函数在实际应用中的优势和劣势展开分析后,本文提出了新的函数,该函数加入了调节因子和半软阈值因子μ和β,其表达式见下:

(5)

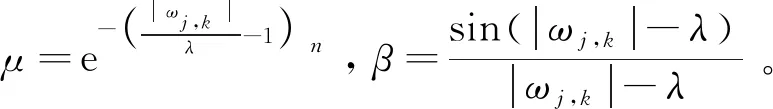
图4 新阈值函数示意图

3.2 对构造的新阈值函数的分析

(1)新阈值函数的连续性

当ωj,k→λ时,

(6)

故:

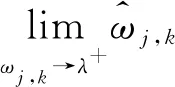
(7)

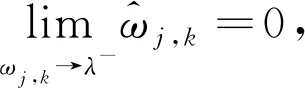
同理:

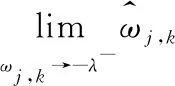
(8)

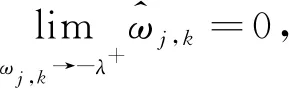
综上所述,本文构造的新函数在±λ均连续,新函数的连续性表明改进的阈值函数能够避免吉布斯震荡的产生。

(2)新阈值函数的渐进性

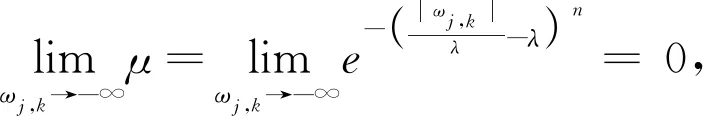
故1-μ=1

(9)

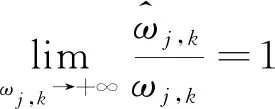
(3)新函数的偏差性

(10)

(11)

综上所述:

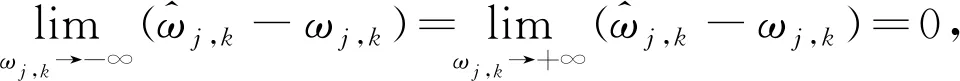
因此,从数学角度的分析,调节因子μ的引进使新的阈值函数具备灵活可变的特点,当ωj,k→±λ时,新函数在±λ处具有连续性,有效地规避了硬阈值函数不连续的缺点；而随着ωj,k取值越大,其与真实小波系数恒定偏差越小,在极限的情况下偏差消失。

4 仿真与分析

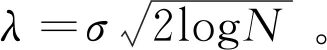
表4 三种阈值函数处理Doppler含噪信号后的信噪比和均方根误差对比

对图5～图8分析可知,相比于软、硬阈值函数,含噪信号利用本文提出的新阈值函数处理后,能够获得更优良的效果,图像中的曲线更平滑且图中阴影部分更少,而从表1～4上展开比较,“blocks”的含噪信号经本文阈值函数去噪后,信噪比(SNR)相比于软、硬阈值函数分别提高了0.8866 dB、5.6824 dB,均方根误差(RMSE)相比于软硬阈值函数分别降低了0.1924、0.0255。相应的“bumps”的去噪信号信噪比(SNR)分别提高了1.2492 dB、1.5735 dB,均方根误差(RMSE)相比于软硬阈值函数分别降低了0.2433、0.0221；“heavy sine”的去噪信号信噪比(SNR)相比于软、硬阈值函数分别提高了1.4352 dB、1.5003 dB；均方根误差(RMSE)分别降低了0.1137、0.1954；“Doppler”的去噪信号信噪比(SNR)相比分别提高了0.5660 dB、0.9728 dB,均方根误差(RMSE)分别降低了0.1169、0.4283,以上数据表明:含噪信号在经过本文构建的阈值函数去噪后,具有更高的信噪比以及更低的均方根误差,因此本文构建的阈值函数去噪效果更优良。

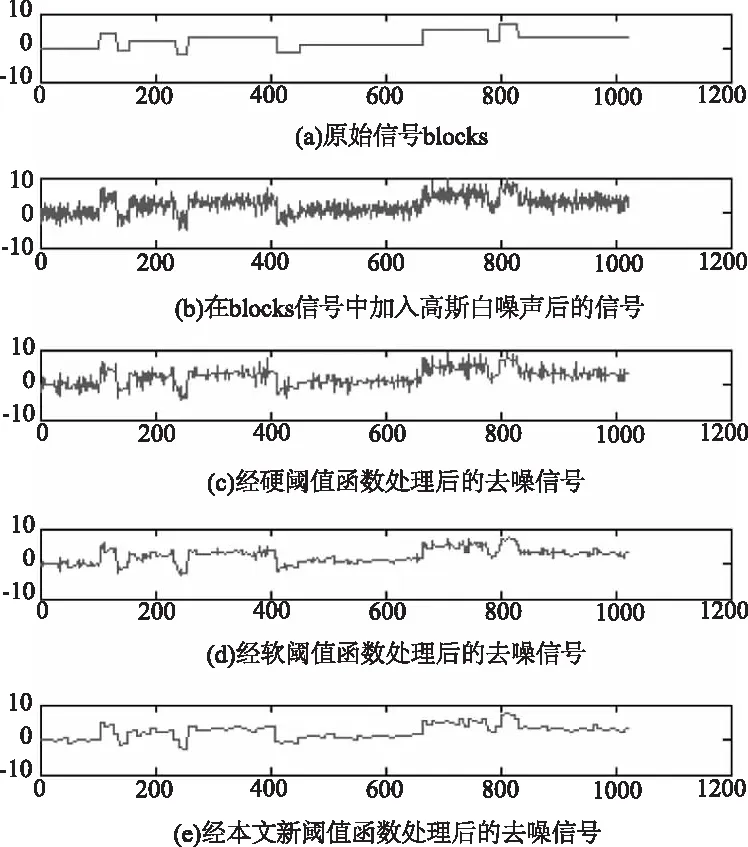
图5 几种阈值函数对blocks信号的处理对比

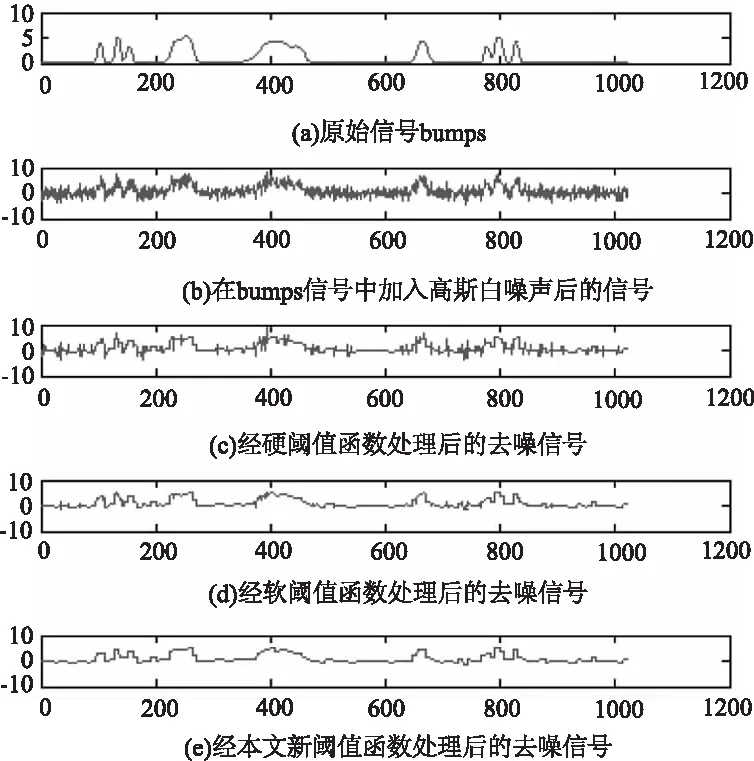
图6 几种阈值函数对bumps信号的处理对比

图7 几种阈值函数对heavy sin信号的处理对比

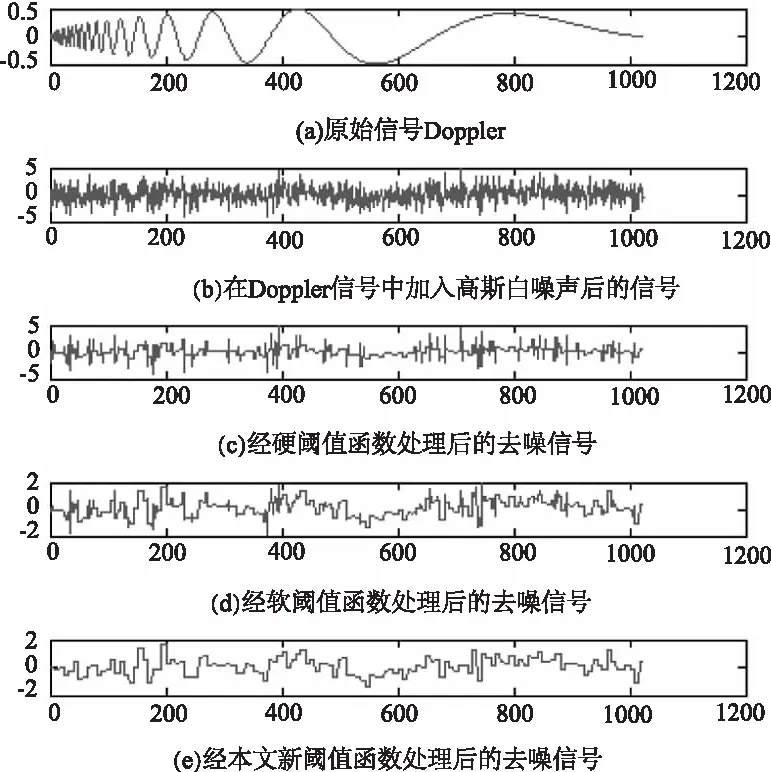
图8 几种阈值函数对Doppler信号的处理对比

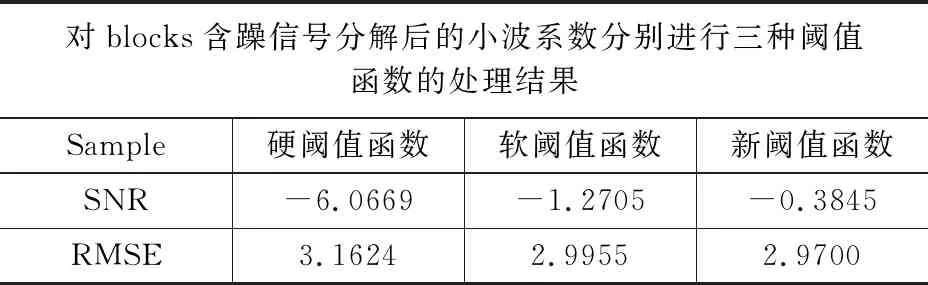
表1 三种阈值函数处理block含噪信号后的信噪比和均方根误差对比

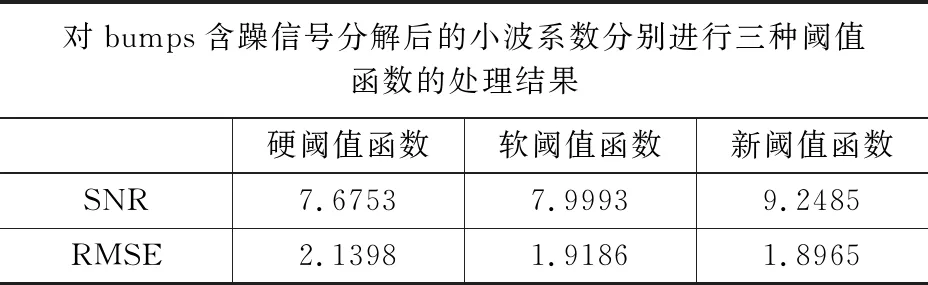
表2 三种阈值函数处理bumps含噪信号后的信噪比和均方根误差对比

表3 三种阈值函数处理heavy sine含噪信号的信噪比和均方根误差对比

5 结 论

本文首先介绍了小波阈值去噪算法的原理及步骤,分析了软硬阈值函数各自的优势和缺点,在兼顾优点的前提下改进了缺点,进而提出了一类新的阈值函数,该函数在调节因子的作用下可以完成向软、硬阈值函数的转变,并且在半软阈值因子的作用下降低了误差。最后通过Matlab仿真可得,本文生成的四种含噪信号采用新阈值函数去噪后,信噪比(SNR)相比于软、硬阈值函数均有所提高,平均提升了0.1034 dB、2.4327 dB,而均方根误差(RMSE)相比于软硬阈值函数均有所降低,平均降低了0.1665、0.1687,仿真结果表明,本文构造的新阈值函数具有可行性,该方法对光纤传感网络解调系统FBG信号的提取、提高波长检测精度、准确寻找波峰位置及降低寻峰误差具有良好的应用价值。