激光损伤测试系统衰减片参数的改进遗传算法优化

李建超,苏俊宏

(西安工业大学光电工程学院,陕西 西安 710021)

1 引 言

在高功率激光使用环境下光学元件的损伤特性对于光学系统的可靠性至关重要。准确测试光学元件的激光损伤阈值是提高抗损伤的必要条件。在损伤测试系统中,激光能量衰减器对作用于被测光学元件表面的激光能量起着调控作用。

20世纪80年代,各国对光衰减器的研究投入了相当的人力和物力。到目前为止,已形成了固定式、步进可调式、连续可调式及智能型光衰减器四种系列。目前国内设计方法主要有机械式调光阑法、光电技术调光法、晶体吸收法、偏振衰减法和吸收式衰减片；国外设计方法主要有:利用内反射原理,改变间隙和透射厚度的双直角棱镜对实现；利用菲涅尔原理的旋转光楔对实现衰减[1-3]。这些方法各有利弊。本系统采用的是轮盘式中性密度滤光片以三组级联方式实现的激光能量衰减,能量衰减率间隔最大值为测试激光能量的12 %,最小为5 %。

精度高是光衰减器的重要指标,在本系统中,对激光能量的测试是离散的并不连续,这就要求各一个测试点间隔尽量一致且细分程度越高越好,直接影响着系统的测试精度。因此,针对这一问题,本文利用解决多目标、多模型的优化算法——遗传算法[4-8]并进行了改进,实现了衰减片参数的优化,提高了系统测试精度。

2 激光损伤测试系统

本激光损伤测试系统如图1所示,1064 nm高能脉冲Nd∶YAG激光器发出测试激光,经轮盘式级联式中性密度滤光片的衰减,经汇聚透镜,分束镜,辐照样片,测试样片损伤阈值。

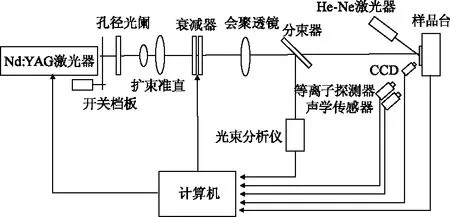
图1 薄膜激光损伤判别系统

图2为衰减器结构,图2(a)为衰减盘的级联情况,系统由3个衰减盘组成；图2(b)为衰减片在衰减盘上的分布,其中为使整个系统的能量调节能达到测试激光器的最大值,在每个衰减盘的5个衰减工位中,设计一个衰减率为0的工位。其余4个工位为0 %～99 %范围内不同衰减率的衰减片,3个衰减盘级联,通过不同衰减片的组合,形成不同衰减率组合。

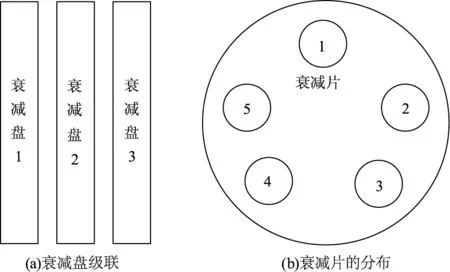
图2 衰减器结构

对三个衰减盘不同的衰减值种类及分布,达到衰减后的激光能量值间隔和线性度达到所需求的最佳的目标值,这是一个典型的多约束目标求解的问题,而遗传算法在对于参数组合的多样性和复杂性提供了较好的解决方案,考虑到该衰减片参数设置的特点,本文采用遗传算法作为解决衰减片参数优化的算法。

3 遗传算法

遗传算法(Genetic Algorithms,GAs)是基于自然选择和自然遗传机制的搜索算法,它是一种有效的解决最优化问题的方法。遗传算法最早是由美国Michigan大学的John Holland和他的同事及学生提出的。类似于自然界演化的基本法则,“适者生存”是遗传算法的核心机制,同样,复制(reproduce)、杂交(crossover)、变异(mutation)等自然界的生物演化规则在遗传算法中都得到类似的体现。图3为基本遗传算法流程图。

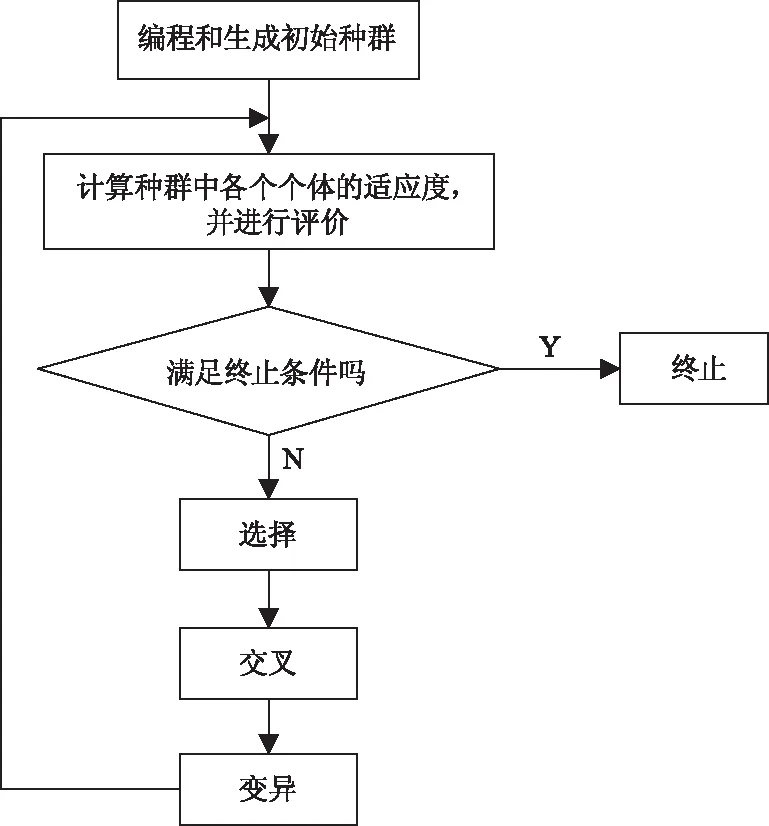
图3 基本遗传算法流程图

4 衰减片参数优化算法研究

4.1 编码方案

在遗传算法中,首先应初始化,即确定参数的个数并随机赋值。在本测试系统中,采用3组5片衰减片级联形式,且含有一个衰减率为0的衰减片。除去每个衰减盘上的0衰减片工位,剩余12片衰减工位,衰减片的种类未知数,也就是说,遗传算法中的参数个数不确定,因此存在种类数和不同种类数情况下每一衰减片的具体衰减率值及分布两重优化问题。为使优化简便,预设衰减片的种类分别为6、7、8、9、10种,然后分别用遗传算法编写程序进行优化。

考虑到搜索范围和精度要求,同时实数编码可避免频繁的编码和解码,提高算法运行效率,因此本文采用实数编码方式。根据不同衰减种类数,每一个体设置不同位数。以8种不同衰减率为例,一个个体代表一条染色体,一个参数代表染色体上的一个基因点,每一个个体设置11位数,即每条染色体上有11个等位基因,其中编码前三位分别代表三种盘符,其中1,2,3,4,5,6,7分别表示7种不同衰减率的衰减片,0代表衰减率为0 %,包括0共8种不同衰减率,其中,7个不同衰减值分别在4～10位表示,每一位数字代表的衰减值是优化的对象,0必须有,无需优化,不占基因点位,第11位为个体的适应度值,很明显,适应度越大,染色体越接近目标值,所以3个衰减盘8种衰减度值及自身的适应度值共11位数组成。同理,9种不同衰减率就由12位数组成。

一般情况下二进制编码与十进制编码相比优点在于编码、解码操作简单,交叉、变异等遗传操作便于实现。因此,本文采用二进制编码的遗传算法。

4.2 适应度函数的选取

遗传算法在优化搜索中以适应度函数为寻优依据,在本算法中,对于一个个体,每个盘上有5个不同的衰减率数值,理论上根据共有125种组合,由于只有8种衰减值,所以125种必有组合结果相同的衰减率,须去除相同结果的组合,将剩余衰减率从小到大排序。设置变量N,初始化为3 %,同时设置变量x,初始化为0；将排好序的衰减率相邻两数两两做差,其中,差值如果在[0,3 %]范围内,则X加1,负责,X=1。故每一个体都有一个X值,而这个X的大小就是这个个体的适应度值,X越大,则均匀性越好,选出X值最大的那个个体,即为最优解。

4.3 遗传算子的改进

4.3.1 选择算子

本算法在进行选择时把适应度值排序和随机选取相结合,对父代中的个体根据适应度进行了排序,然后对前50 %个体进行随机选择,这样不仅能将父代中优秀的个体复制给下一代,而且还能有效的避免陷入局部最优。

4.3.2 杂交算子

杂交往往是根据交叉概率通过对父代两个个体的部分结构进行替换重组而得到新的个体,但交叉概率太大或太小都会影响算法寻找全局最优,在本算法中,我们没有采用交叉概率这个限制条件,我们采用的是在对父代选择的两个个体必然会产生交叉的基础上,通过随机交叉两个个体的部分基因的方案,这样不仅提高了算法的效率,而且产生的新个体使组合的新种群多样性更大,这样更利于达到全局最优。

4.3.3 变异算子

本算法是对杂交后的个体继续进行变异,对表述个体的实数值进行二进制化,然后根据交叉概率的大小而对个体进行位操作,即就是1～3上的值(<35)分别和2,4,8,16,32进行了与操作,对于4～10上的值(<1024)进行了同样的操作。这样做能够保持变异的范围在给定的条件内。

4.4 遗传算法的实现

根据参数的种类而决定种群规模的大小,设定算法的终止条件是达到进化代数,记录每一代的个体对应的适应度值,选出适应度值最大的那个个体。算法流程图如图4所示。

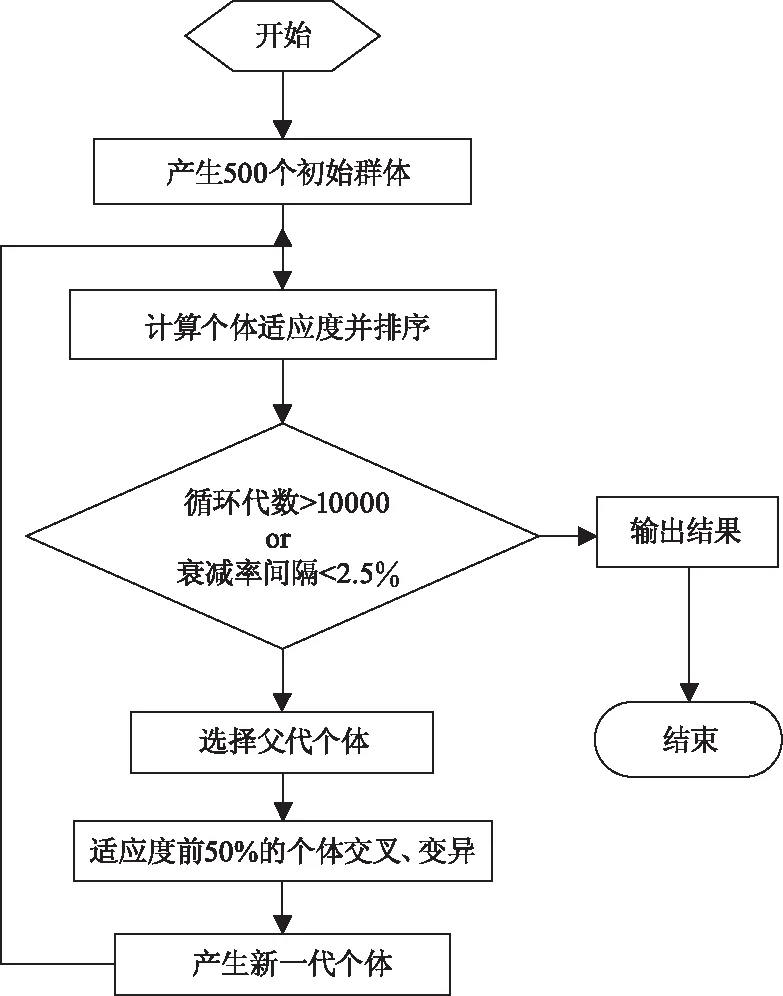
图4 改进遗传算法流程图

(1)初始化,并预先随机产生500个个体。

(2)计算、记录每一个个体的适应度值。

(3)根据适应度进行排序,在前50 %的个体中随机选择父本进行交叉,变异,生成200个新个体。

(4)对新一代200个个体进行适应度计算且记录,并根据适应度选出700个个体中最佳的500个个体准备进行下一次重复操作。

(5)判断:如果满足终止条件则输出结果并结束程序,否则继续。

(6)根据记录的所有的适应度值选出其最大的值所对应的个体,而此个体即为优化结果。

5 优化结果

图5是分别对于6,7,8,9,10种衰减度值在相同的约束条件下(精度要求小于3 %,循环代数10000次)所得到的适应度值分布图,从图中可以看出当三个盘上的衰减度分别由6和7个不同值组合时,其适应度都值为0,也就是没有满足要求的组合,而当其组合变为8个数字时,其适应度值是86,当衰减度个数再增加时,适应度值也逐渐随之增加,而根据我们的要求,在满足精度要求的情况下,衰减度的个数当然越少越好,所以当衰减度个数为8时,所组合的结果是最佳的。

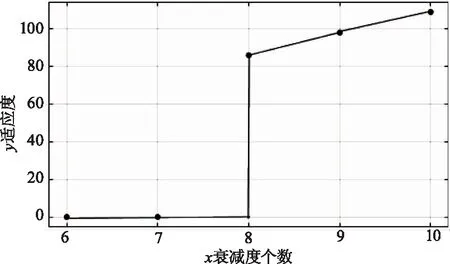
图5 适应度与衰减度个数关系图

图6是8种衰减度值所产生的适应度值随着循环代数的增加而变化的曲线图,从图中可以看出,随着循环代数的增加,适应度值在逐渐的增大,等到循环代数达到8000次时,适应度值基本不再增加。

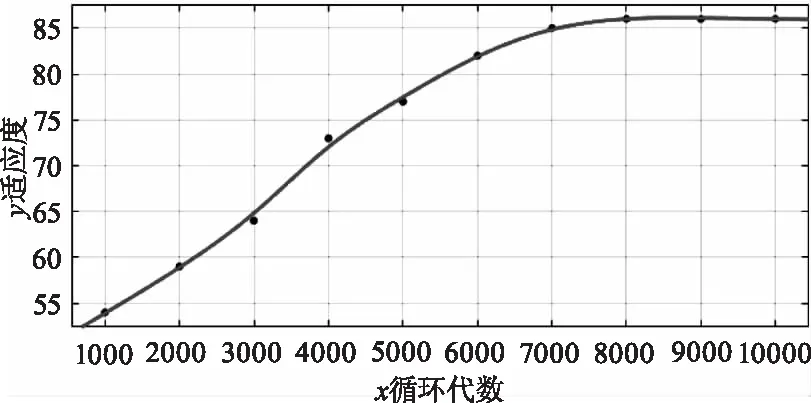
图6 适应度与循环代数关系曲线图

图7是8种衰减度值级联组合而成的衰减率分布情况,在0和1之间分布着85个衰减率值,每两个衰减率差值小于3 %,线性度为12.4 %。三个盘上的衰减度值分布如下(T(1),T(2),T(3))。

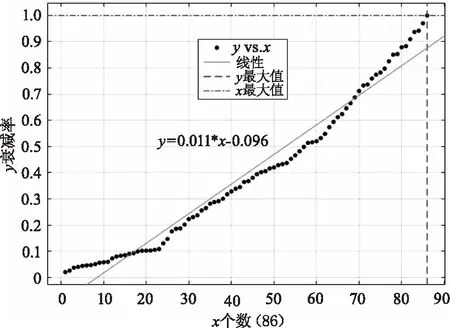
图7 8种衰减度值级联衰减率分布图

T(1)=0,1,2,6,7(0,0.938,0.851,0.433,0.971)

T(2)=0,1,3,4,5(0,0.938,0.782,0.108,0.548)(不同衰减盘上的衰减度分布)

T(3)=0,3,5,6,7(0,0.782,0.548,0.433,0.971)

T(4)=1=960 960/1024=0.938T(5)=2=871 871/1024=0.851T(6)=3=801 801/1024=0.782T(7)=4=111 111/1024=0.108T(8)=5=561 561/1024=0.548T(9)=6=443 443/1024=0.433T(10)=7=994 994/1024=0.971(每个数代表的衰减度)

T(11)=86(适应度值)

实验结果表明:改进后的遗传算法具有以下优点:①相同约束条件,衰减盘参数的线性度和参数的个数存在近似的线性关系；②在参数个数确定的情况下,衰减盘参数的线性度随着进化次数的增加而增加；③当参数个数达到8种时,进化代数达到8000次时,可稳定求解出最优解。

6 总 结

本文利用遗传算法并进行了改进,优化了激光损伤测试系统衰减片参数。其中,实数编码的改进,使每个个体能够记忆其属性值和适应度值,提高了算法的效率；选择算子中,结合适应度值排序和随机的选择方法,不仅使父代优秀个体向子代转移,而且还能有效的避免陷入局部最优；交叉算子中,采用父代必然发生交叉的策略,所产生新个体的种群、多样性更大,加快全局最优的逼近速度。实验结果证明这一改进遗传算法的可行性,同时得出3组15片中,采用衰减率分别0,0.938,0.851,0.433,0.971；0,0.938,0.782,0.108,0.548；0,0.782,0.548,0.433,0.971的组合能达到最优的组合效果,组合后两衰减率差值小于3 %,线性度为12.4 %。