桥梁滚轴板式伸缩装置摩阻力研究

余祥兴， 佟蕴哲， 刘雨彤， 罗 辉

(1. 贵阳地铁置业有限公司， 贵州 贵阳 550081； 2. 中国建筑国际集团有限公司， 广东 深圳 518057； 3. 华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

桥梁在使用过程中会因温度变化、荷载作用和材料收缩徐变等因素产生结构变形和错位[1～3]，为避免上述因素导致结构损坏，在桥梁上设置伸缩装置来弥补结构变形。桥梁伸缩装置主要有对接式伸缩缝、钢制式伸缩缝、橡胶剪切式伸缩缝、模数式伸缩缝、无缝式伸缩缝[4～6]。以上伸缩装置均存在不足，如型钢模数式伸缩装置，表面的钢板间隙较大造成路面不平[7]，车辆通过时出现跳车现象，同时伴随噪音，当使用年限较长时，内部的螺栓连接件易松脱或断裂[8]，较大的顶面型钢缝隙容易积存不易清理的残留物，长时间使用影响连接件的工作性能[9]，从而对整体结构带来不利影响。

为弥补上述不足，提出滚轴板式伸缩装置[10]，该装置包括伸缩板、若干滚轴板、盖板、弧面支架、定位安装板、盆式橡胶支座、倒L型端支墙及梁缝复合橡胶防水布，盖板和滚轴板上表面形成可伸缩调节并与桥面铺装层平齐且平整无障碍的顶面，伸缩板和滚轴板构成的整体底部设有弧面支架，盖板和伸缩板远离搭接处的外侧底部均通过盆式橡胶支座支承在定位安装板上，且端部倒扣在对应的倒L型端支墙内侧，定位安装板底部通过焊接的预埋U形钢筋与梁端结构固定。该伸缩装置结构新颖、构造简单、耐久性好，特别适用于弯桥、坡桥、斜桥和大型梁缝，可实现桥梁伸缩缝装置表面平整无障碍，行车平稳过渡，避免跳车(见图1a)，一般可适用于80～3000 mm的伸缩范围。

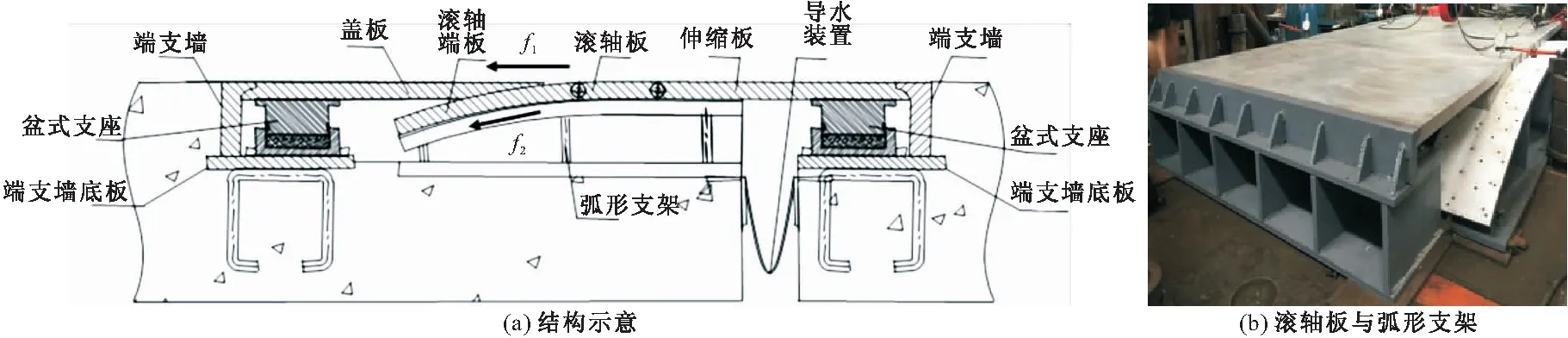
图1 滚轴板式伸缩装置

与传统的伸缩装置不同，滚轴板式伸缩装置的滚轴板和其他部件之间发生相对位移，同时伴有摩擦力[10]，摩阻力过大，伸缩装置有可能出现卡顿，无法实现长度拉伸或恢复原位，有必要对伸缩装置工作时的内部摩擦阻力进行探究。滚轴板式伸缩装置自身的摩阻力主要来源于两个方面，一是固定端盖板与滚轴板之间的摩擦，另一个是滚轴板与弧形支架之间的摩擦(见图1b)。因此需重点研究摩擦力是否满足要求，及摩擦力在总摩擦力中的占比，并探求减小伸缩缝摩擦力的改进方向，为今后的设计施工提供指导意见。

1 试验方案

为测试伸缩装置的摩擦阻力，包括盖板和滚轴板之间的摩擦阻力以及滚轴板和弧形支架的摩擦阻力，将整个试验分为3个工况(见图2)，根据3个工况的试验数据运算得到伸缩装置的摩阻力，与《桥梁滚轴板式伸缩装置暂行技术条件》的规范要求进行对比，即单元拉伸、压缩时最大水平摩阻力小于等于7.5 kN。

图2 试验工况

摩阻试验示意图如图3(图中：Fd为推拉装置总拉(推)力；Ft为轮胎与伸缩板表面的滚动摩擦力；Fg为活动端底滚轴与固定底板之间的滚动摩擦力；f1为盖板与滚轴板之间的滑动摩擦力；f2为滚轴板与弧形支架之间的滑动摩擦力；N为车轮荷载正压力；G为结构部分自重)所示，为模拟路桥的车辆荷载，在千斤顶端头处安装一直径为300 mm的钢轮(见图4)，钢轮经15 mm厚的橡胶包裹处理，在移动端盖板上方用千斤顶施加水平拉、压力(见图5)。竖向荷载和横向荷载均通过千斤顶上的传感器输入到动态信号测试分析系统中，在移动端一侧设置激光位移传感器控制移动端的水平位移。

图3 滚轴板式伸缩装置试验示意

图4 竖向加载装置图5 水平加载装置

初始状态下，车轮荷载加载70 kN的竖向压力，同时利用动态信号测试分析系统记录压力实时变化以保证持荷稳定，稳定后施加水平拉力缓慢拉动移动端300 mm，同时通过动态信号分析系统实时提取拉力和激光位移计的数值，为保证数据稳定可靠，拉动的速度控制在0.1 mm/s，拉力和位移每秒采集20组。所用试验仪器如表1所示。

表1 试验所用仪器 kN

工况1：完整装置的推拉阶段

水平千斤顶推拉3次，测量千斤顶的拉力Fd，此时装置含有4种摩擦力(参见图3)。

Fd1=Ft+Fg+f1+f2

(1)

工况2：去掉盖板装置的推拉阶段

去掉盖板，减少了盖板与滚轴板之间的滑动摩擦力，进行3次推拉，此时装置含有3种摩擦力(参见图3)。

Fd2=Ft+Fg+f2

(2)

工况3：去掉盖板和滚轴板装置的推拉阶段

去掉盖板和滚轴板，减少了盖板与滚轴板之间的滑动摩擦力以及滚轴板与弧形支架之间的滑动摩擦力。为保持支撑，在移动端盖板下方安装支撑轮(见图6)。轮子表面和轮轴做润滑处理，降低轮子和盖板底面的摩擦系数，该摩擦属于滚动摩擦，故此影响忽略不计。进行3次推拉，测量千斤顶的拉力Fd，此时装置仅含2种摩擦力(参见图3，增加小轮的摩擦忽略不计)，其他保持不变。

Fd3=Ft+Fg

(3)

图6 盖板下方支撑轮

伸缩装置的摩擦阻力，包括盖板和滚轴板之间的摩擦阻力以及滚轴板和弧形支架的摩擦阻力，按式(4)～(6)计算。

f1=Fd1-Fd2

(4)

f2=Fd2-Fd3

(5)

f=f1+f2=Fd1-Fd3

(6)

2 试验结果分析

本试验每个工况进行3次，共得到902790组数据，绘成折线图如图7所示。

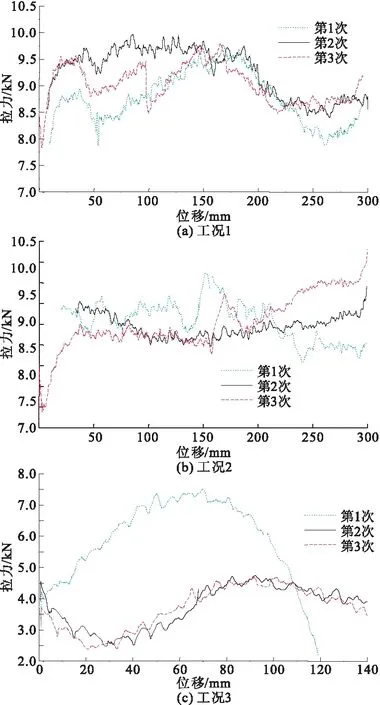
图7 各工况拉力-位移曲线

每组工况各推拉过程拉力均值如表2所示。

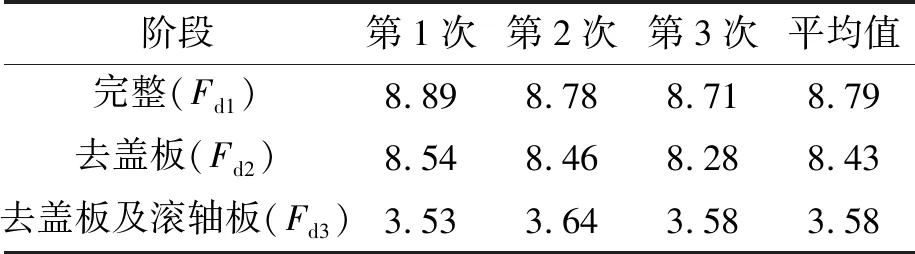
表2 3个工况各推拉过程拉(压)力平均值 kN

根据式(4)～(6)求得伸缩装置的摩擦阻力f，包括盖板和滚轴板之间的摩擦阻力f1以及滚轴板和弧形支架的摩擦阻力f2，结果如表3所示。

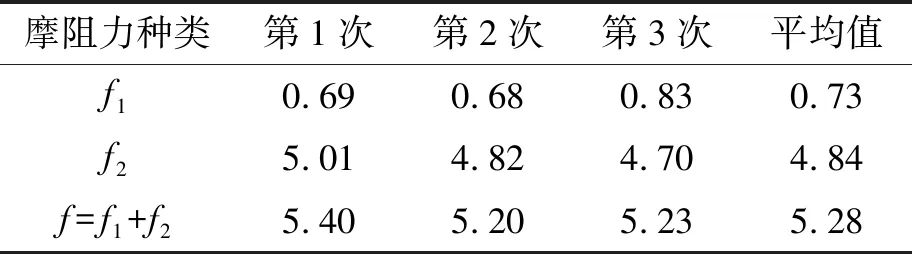
表3 3个工况各推拉过程摩阻力计算结果 kN

由表3可知，3次试验计算结果的平均值为5.28 kN，伸缩装置的摩擦阻力均小于7.5 kN，试验数据真实可靠，满足试验要求。由方差标准差计算公式(7)可得：伸缩装置的摩擦阻力3次测量结果方差为s= 0.09，方差s小于0.10，试验结果稳定。

(7)

3 数值仿真分析

3.1 模型简化与假设

试验装置含有多个滚轴套筒和滚轴板，结构形状多样，接触面多且复杂，由此做出如下简化：

(1)弧形支座及端支墙，原试验装置构造为多块板材焊接而成，为计算简便，设为实心弧形支座，轮廓不变，端支墙等效为等宽(1500 mm)长方体，简化后不影响结果；

(2)通过多次试验确定合适的摩擦因数，代替弧形支架上表面的聚四氟乙烯板；

(3)摩阻力试验中，将轮胎滚动摩擦简化为长方体与盖板之间的滑动摩擦，长方体底面积与轮子和盖板间的接触面积保持一致；

(4)假定滚轴为刚性，即不考虑滚轴的变形。

3.2 数值模型的建立

由于本试验装置考虑重力效应，需设置材料密度和重力加速度，试验装置材料为Q345钢，查阅资料得到相关参数数值如表4所示。

表4 相关参数设定

本模型主要包括有摩擦的面面接触和无摩擦的面面接触，其中滚轴板与弧形支架以及与固定盖板之间的摩擦力为主要研究对象，故均设为有摩擦的面面接触，摩擦因数μ=0.3。滚轴套筒内表面与滚轴外表面之间的相对运动非常微小可忽略不计，故设为无摩擦的面面摩擦。弧形支座和固定端支墙在整个试验过程中均为固定不动状态，因此底面设为固支边界条件。为控制推拉状态，移动端滚轴板的边界条件设为300(-300) mm，模型载荷包括材料自身重力和车轮荷载，建立重力载荷，重力加速度为9810 mm/s2，车轮荷载则是在相应位置设置70 kN的集中力。

为得到精确的结果，划分相对密集的网格，随网格数量的增加动态分析运算量增大，计算速度减缓，对计算机的运算要求越高，综合考虑上述因素，网格类型设为六面体，主要的研究对象，如接触面两侧的单元，最大单元尺寸设置为10 mm，其他部分最大单元尺寸设置为20 mm。网格划分结果如图8所示，共划分20080个六面体网格，经网格质量检查后未发现报错和警告的情况。

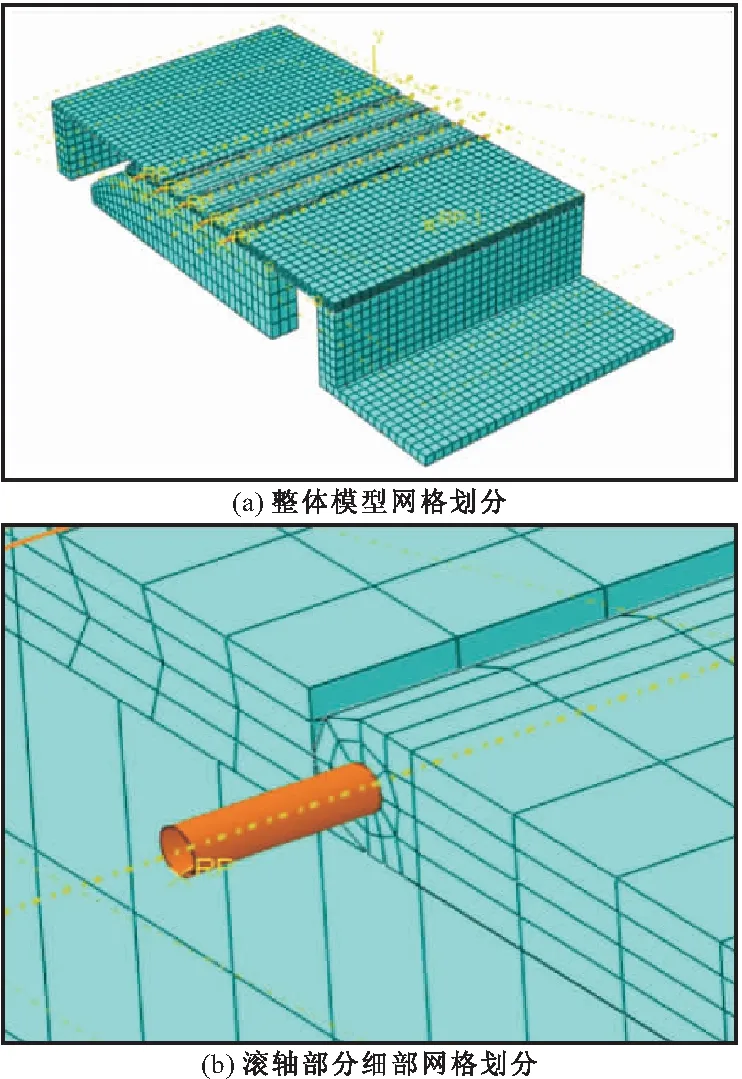
图8 有限元模型

3.3 数值模型结果分析

为简化表示，滚轴板编号示意图如图9所示。提取各个摩擦力并绘制摩擦力-位移曲线如图10所示。

图9 1～6号滚轴板示意

图10 摩擦力-拉动位移曲线

仿真分析所得摩擦力结果如表5所示。

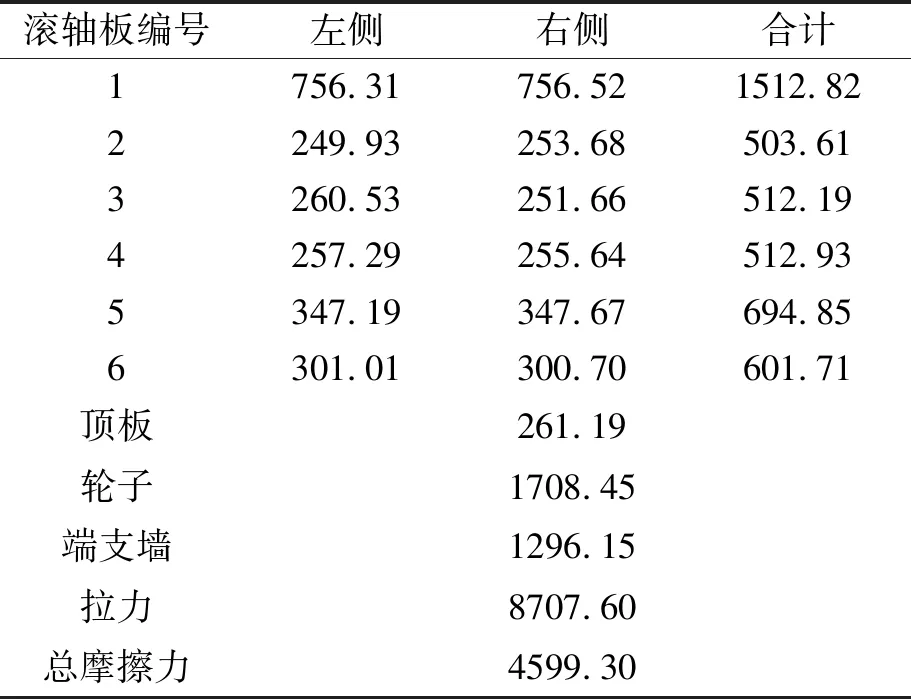
表5 拉动过程各接触面的摩擦力 N

数值模拟采用边界加载方式，场量输出可直接输出各个接触面的摩擦力，伸缩装置的摩擦力由各个滚轴板与弧形支架的摩擦力以及顶板下侧与滚轴板之间的摩擦力构成，对上述摩擦力求和得到伸缩装置的整体摩擦力，如式(8)所示，拉动过程中总摩擦力为4.60 kN，满足规范要求。

整体摩擦力按式(9) 计算。

f=fu+(f1+f2+…+f6)

(8)

式中：fu为滚轴板与盖板之间的摩擦力；f1，f2，…，f6为1～6号滚轴板与弧形支架之间的摩擦力。

1～4号滚轴板的整体摩擦力基本保持平稳，而5，6号滚轴板在推拉过程中和固定盖板接触，其摩擦力-位移曲线出现突变，相应的盖板摩擦力突然减小。分析水平方向的作用力，总摩擦力为4.60 kN，包含1～6号滚轴板和弧形支架及和顶板间的摩擦力，另外轮子与盖板间的摩擦力为1.71 kN，端支墙与地面间的摩擦力为1.30 kN，加和后为7.61 kN，与拉力8.71 kN基本满足平衡关系，其差值主要来源于滚轴板重力水平方向的分力。

对比分析数值模型与现场试验的结果数据，包括伸缩缝端部拉力和移动端支墙上下两侧摩擦力。试验工况1得到千斤顶拉力变化曲线(见图11)，工况3中，千斤顶拉力的平衡力包括加载点的摩擦力、端支墙底座的摩擦力以及后续加装小型支撑轮的滚动摩擦力。仿真模拟中可直接得到加载点和底座的摩擦力，对比工况3的拉力和仿真中两个摩擦力的合力，从而验证模型的正确性，对比数据如表6所示。

图11 千斤顶拉力-位移曲线

表6 摩阻力试验数值分析与试验结果对比 N

由表6对比仿真结果与试验结果可知，对应位置的拉力和摩阻力基本吻合且满足试验标准，曲线变化趋势基本吻合，试验结果曲线在仿真曲线上下小范围波动，说明伸缩装置摩阻力的仿真模型及参数可为实际应用提供理论参考，即应用ABAQUS模型有效模拟实际伸缩过程中的摩擦阻力等物理特性，并基于此做进一步探究。

1～4号滚轴板只做平动，且未与顶板接触，所以1～4号滚轴板的摩擦力均围绕一定值上下波动，而5，6号滚轴板运动过程中，出现摩擦力突变，这是因为在拉动过程中，滚轴板先接触盖板后脱离盖板，当盖板压力逐渐减小至0时，滚轴板与盖板的摩擦力则会降低，而推动过程相反。

1号滚轴板所受摩擦力较大，2～4号滚轴板摩擦力相互接近，较1号滚轴板摩擦力小500 N左右。计算各个部位摩擦力(1～6号滚轴板)占整体摩擦力百分比如表7所示，1号滚轴板摩擦力占比33%左右，远大于其他位置滚轴板摩擦力占比，这是由于2～6号滚轴板规格相同，且质量仅为1号滚轴板的1/4左右。5，6号滚轴板摩阻力占比稍大于2～4号滚轴板，这是由于当5，6号滚轴板移动到固定盖板下侧时，盖板对其产生压力使得摩擦力出现一定幅度的增大。

表7 伸缩装置各部位摩阻力占比 %

整个伸缩装置使用过程中，应重点关注1号滚轴板下方的摩擦力、5号滚轴板与6号滚轴板的摩擦力，可从上述部位对整个伸缩装置的伸缩性能进行改良。根据实际伸缩量的要求增减伸缩装置滚轴板的数量，当伸缩装置应用于对摩阻力要求较高的工况时，采取适当措施降低1号滚轴板接触面的摩擦因数，如改进涂层材质，或在保证固定盖板强度的前提下，适当降低盖板重量，以提高伸缩装置的伸缩性能。

4 结 论

本文提出一种滚轴板式伸缩装置，并针对其摩擦阻力进行室内试验与仿真分析。首先进行室内试验得出伸缩装置不同构件间的摩阻力，及伸缩装置整体的摩擦阻力小于或等于5.28 kN，满足规范要求。然后进行数值仿真分析，根据3个工况下的试验结果和数值计算结果表明了模型的正确性，并计算伸缩装置不同部位滚轴板的摩阻力占比，实际使用中应重点关注摩阻力占比较大的1号滚轴板、5号滚轴板和6号滚轴板，为桥梁滚轴板式伸缩装置的改进优化提供理论参考。