基于冲突成像概率的多星任务预调度算法
2020-09-23徐明明王俊峰
徐明明,王俊峰
(1.四川大学计算机学院,成都 610065; 2. 四川大学空天科学与工程学院,成都 610065)
1 引 言
对地观测是卫星一个非常重要的应用,据联合国外太空事务局(UNOOSA)记录,截至2018年底,有601颗对地观测卫星仍在轨运行,约占全球在轨卫星总数的33%[1].卫星成像主要采用光学成像方式,其中小部分通过雷达等方法成像.当卫星经过目标上方时,称之为“过顶”,此时卫星与目标之间可见,卫星才能对目标进行成像.卫星的数量和传感器的分辨率都在逐年上升,但卫星的瞬时视野依然受限,对地观测需求不断增大,且发射卫星的费用非常高昂,卫星的工作寿命也很短暂,卫星资源仍然紧缺,为了缓解这一问题,大量研究者针对对地观测任务调度模型和算法进行不断优化和改进,力争在满足任务和资源约束的条件下为每个任务更加合理地分配卫星资源和决定任务的执行时间段.
对地观测任务调度可分为单星调度和多星调度.早期的研究大多针对单颗卫星资源进行调度,随着观测任务日益繁重,卫星数量也不断上升,如果采用单星调度,调度系统内缺乏通用性,卫星的观测能力得不到充分利用.如何综合利用卫星网络,高效的整合卫星资源,全面地发挥多卫星系统的观测能力成为各国研究的重点.卫星调度问题是一个NP难问题[2],无法在多项式时间内找到该类问题的最优解,只能通过离散化和次优化,在可接受的时间内找到较优解,主要的研究方法可分为确定性算法,搜索算法或启发式算法:① 确定性算法中采用较多的是分支定界法[3-5],该算法需要消耗大量的空间来存储叶节点的边界.当界定方法不适合时,分支定界法的性能退化至接近穷举法;② 搜索算法在多星调度问题上广泛使用,包括蚁群优化算法[6]、遗传算法[7]、爬山算法[8]、禁忌搜索算法[9-10]和模拟退火算法(Simulated Annealing,SA)[11]等,这种方法得到的解质量较高,但搜索空间较大时,计算时间较长,并且有陷入局部最优的风险;③ 启发式算法基于先验信息制定任务调度规则,Chen等人[12]提出了几种基于优先级和冲突避免的启发式策略,并开发了基于时间的贪婪方法,基于权重的贪婪方法,以及改进的差分进化算法.Cho等人[13]重新定义多星调度问题为旅行商问题的变体,并结合一种典型的基于邻域搜索的路径改进算法——Lin-Kernighan-Helsgaun启发式算法来解决该问题.王慧林等人[14]针对异构地球观测资源网提出了两种算法用以协调和分配观测任务,包括最高权重优先分配算法和禁忌列表模拟退火算法.该类算法规则较为复杂,设计思路的偏离将造成性能与最优解相去甚大.
为了提高卫星调度系统的灵活性和鲁棒性,Morris等人[15]提出了一种分布式的调度模型思路:将多星调度分解为两个子问题,预调度和单星自主调度.首先,为每个任务分配卫星资源,然后每个卫星执行自主单星调度算法.但他们只描述了框架的模型,并没有针对上述框架提出具体的策略.已有一些研究者采用基于分解的分布式模型来进行多星观测调度:李菊芳等人[16]采用自适应蚁群优化算法搜索最优的任务分配方案,在单星自主调度阶段采用非常快速模拟退火算法.实验结果表明,对比于禁忌搜索算法,性能提升并不明显(<8%).孙凯等人[17]提出了一种新的学习型遗传算法来解决任务资源匹配问题,并采用后移滑动策略及最优插入位置搜索策略解决单星任务调度子问题.Sinha等[18]提出了一种基于多代理的卫星系统建模方法,并利用最大增益消息算法处理卫星中的任务分配问题.当搜索算法应用于多星预调度阶段时存在缺陷:根据后续的单星调度阶段的结果更新解的适应度,完成反馈,导致预调度算法和单星自主调度算法的耦合.此外,搜索算法的终止条件和初始值的设定也会影响性能,设置不当会导致分配方案不合理.
针对以上问题,本文提出了一种基于规则的启发式算法,适用于分布式的卫星任务规划系统,其目标是在预调度阶段,考虑能量约束,化解任务之间的冲突,完成优化目标,并且通过将计算负载从单个节点分散到多个来减少计算时间,从而提高系统的效率和稳定性.该预调度算法实现简单,通用性强,只需卫星和任务的先验信息,后续的单星自主调度阶段的算法可以结合实际情况自由选择,无需编写反馈接口.
2 多星成像任务调度模型
2.1 多星成像任务调度模型输入与数据的预处理
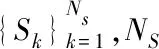
根据图像卫星的特点,作如下假设.
① 用户提交任务后,无法撤回或更改;
② 用户无法在任务规划期间提交任务;
③ 一个任务可能有几颗卫星可以执行它,但最终只能由其中一颗卫星执行;
④ 卫星在一个运行周期内对一个任务目标点最多只能有一次观测机会;
⑤ 卫星观测具有原子性,一旦观测任务开始执行就无法被中断;
⑥ 在一个时间点,卫星只能对一个任务目标点进行观测.
基于上述前提假设,本文对多星问题的输入进行公式化表达,卫星和任务的主要参数如表1.

表1 卫星和任务的主要参数Tab.1 Main parameters of satellites and missions
得到输入后,系统进行预处理,通过仿真得到目标点对卫星可见的时间范围,再计算该时间范围与任务的指定观察时间范围重叠的部分,称之为可用时间窗口,表示为
TW={twij|1≤i≤NSC,1≤j≤NT}
(1)
其中,(tw_startij,tw_endij)为卫星i可完成任务j的时间段;mpcij为卫星i完成任务j的最小电量消耗;mmcij为卫星i完成任务j的最小内存消耗.
2.2 多星成像任务调度模型的输出与优化目标
完成预调度后,得到分配矩阵O.
O={oij|1≤i≤Ns+1,1≤j≤NT}
(2)
多星观测调度本质上是一个满足约束的调度机问题,约束条件对于调度过程的制约非常大,从而影响调度结果.本文采用的是超额订购方式,即在给定的松弛程度下,分配到卫星的任务量可以超出卫星的执行能力,σi代表系统的超额分配率.
(3)
(4)
(5)
(6)
其中,SNs+1是一颗虚拟卫星,所有不能被卫星资源调度的任务将分配到该卫星上;式(3)是任务的单一执行约束,即每个任务只能被调度一次;式(4)~(6)是卫星的载荷能力约束,即每个卫星完成分配到的任务数量、所需的总耗电量和存储容量不能超过给定松弛程度下卫星的载荷能力.
预调度是多星调度的第一阶段,因此其优化目标和整个多星调度的相同.当单星调度阶段完成时,分配矩阵O将被更新,主要是因为某些任务在单星调度阶段未能成功调度,只能分配到虚拟卫星上.最终的优化目标是最大化执行完单星自主调度算法后可以成功调度的任务的总优先级,可以表示为
S.t. (3)~(6)
(7)
3 基于冲突概率的调度算法
3.1 算法描述
本节提出CIPBS算法来处理多星预调度问题.该算法的基本思路是在任务分配的过程中,根据当前分配情况计算任务在每个卫星上成功执行的概率,将任务分配给成像可能性最大的卫星.Cho等人[13]提出影响成像概率的因素为当前任务可用时间窗口与同一卫星上其它任务的可用时间窗口的重合程度,但只考虑这一因素是较为片面的,因为在多卫星场景下,时间窗口冲突的多个任务被分配到不同的卫星资源上,相互的影响不一定存在.如图1所示,为了更充分利用多星调度问题的启发式信息,本文将任务分为冲突任务和非冲突任务,冲突任务的冲突成像概率由潜在冲突系数、实际冲突系数和能量系数构成,而非冲突任务只需要考虑能量的约束即能量系数,最终得到预分配结果.

图1 求解策略Fig.1 Solving stategy
预调度阶段的第一步是根据任务间可用时间窗口的重合度,将任务划分为冲突任务和非冲突任务,以简化后期冲突成像概率的求解.如图2所示,mcitij是任务j在卫星i上的可用时间窗口的最长连续无碰撞时长.如果
∃i∈{1,2,…,Ns},mcitij>mdj
(8)
即在卫星i上,任务j的最长连续可用无碰撞时长超过该任务的最小执行时长,则称任务j在卫星i上无冲突.若某一任务在任一卫星上无冲突,就是非冲突任务,否则,该任务是冲突任务.
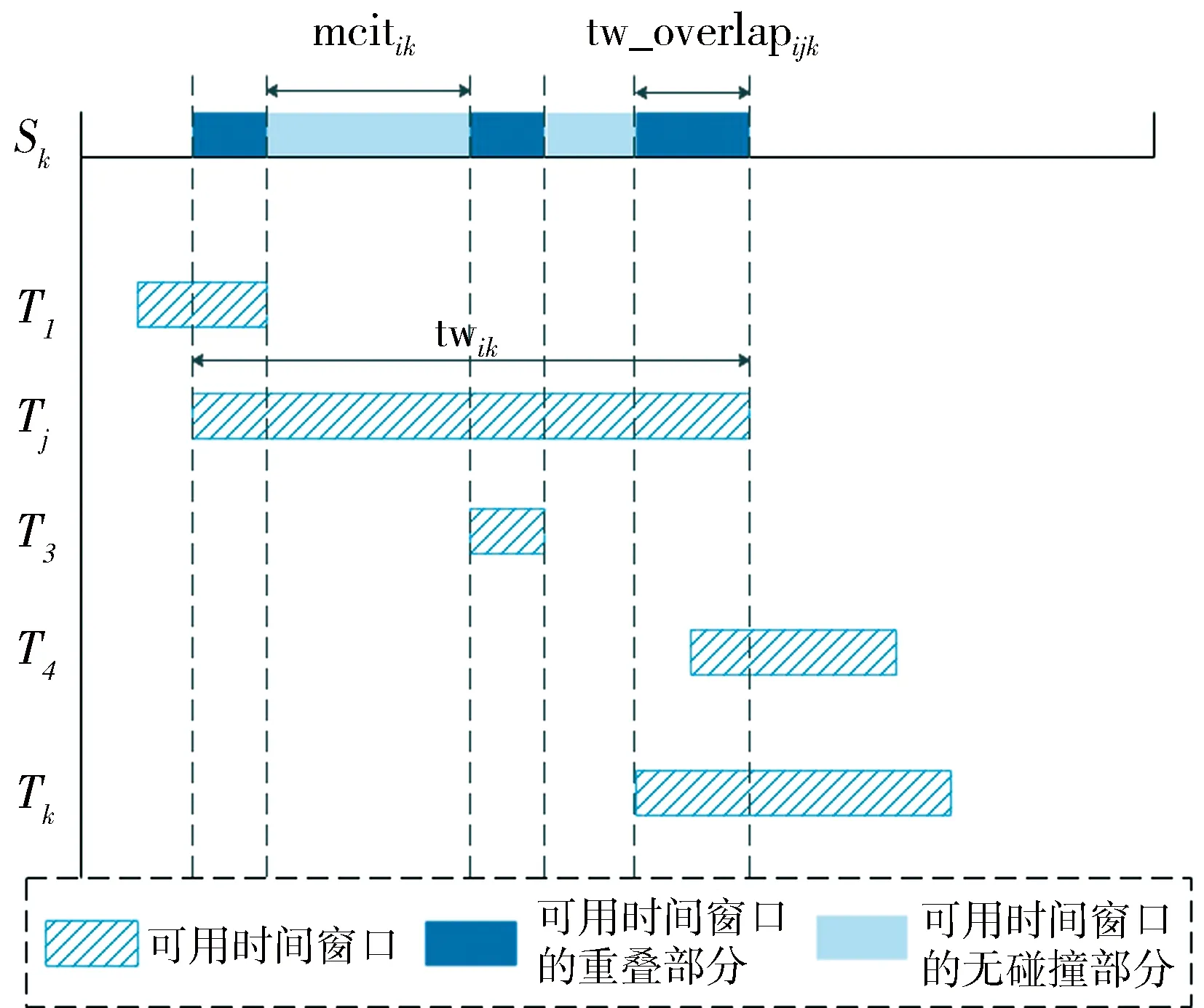
图2 任务最长连续可用无碰撞时长示意图Fig.2 Maximum continuous idle time of the task
如图2所示,冲突成像概率由pij、rij和eij三部分构成,其中,δ为无穷小量如下式.
(9)
其中,pij是潜在冲突系数,反映的是任务间的潜在影响,即尚未分配到卫星i的任务在卫星i上有可用时间窗口,可能在后续的调度中被分配到卫星i上,和任务j争抢时间窗.任务j的潜在冲突系数的计算方法为:找出所有未分配但在卫星i上有可用时间窗口的任务,计算(tw_startij,tw_endij).
(10)
式(9中),rij是实际冲突系数,反映的是任务间的实际影响,即在计算任务j分配到卫星i时的冲突成像概率时,已经有一些任务被分配到卫星i上,如果这些任务和任务j的执行会产生冲突,这种冲突必须在此时最小化.在计算过程中,每个卫星都维护各自的有向无环图用以计算实际冲突系数.记卫星i的图为Gi,其最长加权路径为Gi_longestpath,该图的结点由所有分配到该卫星的任务构成,图的有向边表示任务的执行序列.加入一个任务j时,将任务结点j插入图内构成图Gi',找到该图包含结点j的最长加权路径Gi'_longestpath.所有因该任务无法执行的已分配任务的总权重就是任务j在卫星i上的实际冲突系数rij,可表示为
rij=Gi_longestpath+pj-Gi'_longestpath
(11)
为了系统负载均衡和满足能量约束,要考虑完成卫星分配到的总任务的能量消耗,故定义能量系数的计算如下.
(12)
综上所述,算法1给出了CIPBS算法的详细计算过程.
Algorithm1 Collision Probability-Based Schedule(CIPBS)
1) 生成场景(S,T)
2) 初始化参数
3) 预处理,计算tw,mmp,mpc,mcit
4) forj←1toNtdo
5) fori←1toNSCdo
6) ifMCITij>MDj
7) Φ←Φ∪{Tj}
8) Γi←Γi∪{SCi}
9) end if
10) end for
11) end for
12) while Λ*≠Ø do
13) 随机选择任务Tj∈Λ*
14) fori←1toNSCdo
15) 计算Λ*中每个任务的TW_overlapijk
17) 构建卫星Si上分配到的任务的有向无圈图G
18) 将任务Tj插入G构成G'
19)rij←Gi_longestpath+pj-Gi'_longestpath
22) end for
23) ifcij是{cik|1 24)oij←1 25)G←G' 26) end if 27) Λ*←Λ*-{Tj} 28) end while 31) 依次选择任务Tj∈Λ 32) fori←1toNSCdo 33) ifSi∈Γj 35) elseeij← 36) end if 37) end for 38) ifeij是{eik|1 39)oij←1 40) end if 41) Λ←Λ-{Tj} 42) end while 43) returnO 其中,Φ表示所有无冲突任务的集合;Γi表示所有在卫星上Si上无冲突的任务集合;Λ*表示所有尚未分配的冲突任务构成的集合;Λ表示所有尚未分配的无冲突任务构成的集合. CIBPS算法的时间复杂度主要由三个部分构成(N表示任务规模,K表示卫星规模):1) 划分冲突任务和非冲突任务的复杂度为O(K·N2).其中,计算一个任务在一颗卫星上的最长连续可用无碰撞时长的时间复杂度为O(N),则计算N个任务在K颗卫星上的最长连续可用无碰撞时长的时间复杂度为O(K·N2); 2) 冲突任务调度的复杂度为O(K·N3).其中,对于单个任务在某一卫星资源上计算成像概率而言,计算潜在冲突系数的复杂度为O(N),采用Dijkstra算法构造有向无环图并计算其最短单源路径得到实际冲突系数的复杂度是O(N2),计算能量系数的复杂度为O(N),故复杂度为O(N)+O(N2)+O(N)=O(N2),对于任务规模为N,卫星规模为K的冲突任务调度问题计算时间复杂度为O(K·N3); 3) 对于无冲突任务,只需计算其能量系数,复杂度为O(K·N2).因此,CIBPS算法的总时间复杂度为O(K·N2)+O(K·N3)+O(K·N2)=O(K·N3). 在开始调度时,pij较大,rij较小,此时cij的计算主要取决于任务间的潜在冲突.随着任务分配的进行,每一个任务被分配到卫星资源后,该任务对其他任务的潜在冲突就会在随后的调度计算中被剔除,同时,该任务会被添加到该卫星资源的有向无环资源图中,随着卫星资源的已分配任务信息增多,pij减小,rij增大,此时cij的计算主要取决于任务间的实际冲突.通过这种计算冲突系数分配卫星资源的方式,可以减少多个任务在同一段时间争用同一个卫星资源的情况,以达到均衡合理分配资源的目的. 本文实验运行在4 GB内存的Inter Core i5 3.20 GHz 单核CPU上,卫星和任务目标点之间的可见时间窗口通过Satellite Tool Kit 11.0软件获取,算法实现语言为Matlab.由于在多星观测调度领域,尚无公开的标准数据集[19].为了全面的分析CIBPS的性能,本文设计了三组任务场景,分别对应不同的任务分布情况,任务的具体生成规则如表2所示. 本文将CIBPS与SA算法进行对比,其中,SA算法被Globus等人在实验中证明在各种典型的对地观测卫星调度算法中具有最好的性能[20].为了评估算法的性能,需要完成单星自主调度得到最终的调度结果.本实验中单星调度算法采用了基于权重的贪婪算法[12].SA算法的终止条件设定为最优解在100次迭代中未曾更新.对于每个实验用例,CIBPS与SA都运行了20次.表3给出了3种分布下15个实验用例的计算结果和CPU运行时间. 表2 任务参数生成规则Tab.2 Generation rule of tasks 表3 实验结果Tab.3 Experimental result 可以通过对表3的分析比较CIBPS和SA之间的性能差异.从实验结果中可以看出,随着任务数量的增加,任务调度率逐渐下降,同时,CIBPS的任务调度率在大多数情况下都高于SA的.用例1中,SA可以和CIBPS实现相同的调度结果,这是因为此时的卫星资源相对充足,但SA花费的时间是CIBPS数百倍.当任务数量增加时,卫星资源相对稀缺,任务的可用时间窗口间竞争加剧,此时CIBPS是一种更好的资源分配算法,能够缓解这种竞争,遏制任务完成率的急速下降.因此,随着任务规模的增加,CIBPS的优势更加明显. 在场景a(用例1~3)中,当任务数量较少时,SA的性能接近CIBPS,尽管搜索需要更多时间,SA仍无法找到更好的解决方案,随着任务数量的上升,CIBPS和SA完成率均呈下降趋势,但CIBPS相较与SA仍有10%以上的提升.场景b(用例4~6)下的结果有些不同:当任务数量较小时,CIBPS和SA之间的性能差异也较明显,随着任务规模的增长,SA的完成率快速下降,CIBPS的完成率缓慢下降,仍比SA提高了约20%.场景c(用例7~15)的任务目标点分布考虑实际的对地观测任务包含定期的巡航拍摄和突发的集中观测,结合均匀分布和集中分布的特征,增加了更多的任务.该种场景下,CIBPS和SA的任务完成率介于场景a和场景b之间,性能提升比也是如此.因此,三种任务目标点分布的场景按资源短缺程度有如下排序:b>c>a,而场景b下,CIBPS的性能提升最大,由此可以得出结论,CIBPS更擅长在卫星资源紧缺和任务可用时间窗口冲突大的情况下处理多星预调度问题. 从CPU运行时间的角度来看,当任务规模较小时,CIBPS的计算时间明显短于SA.随着任务数量的增加,CIBPS的计算时间以三次量级增加,这验证了算法分析中对于算法复杂度的推算.综上所述,CIBPS能够完成在多项式时间内高效解决多星预调度问题的目标. 图3 a组实验结果盒图Fig.3 Box plot for Group(a) 图4 b组实验结果盒图Fig.4 Box plot for Group(b) 图5 c组实验结果盒图Fig.5 Box plot for Group(c) 图3~图5是通过箱形图展示所有解的分布,可以看出,在场景a(用例1~3)中,在解空间较小时,CIBPS和SA每次都可以找到到最优解,但是随着任务数量的增长,CIBPS和SA在每次运行后的解可能有所区别,而即使CIBPS算法的最差解也比SA的最佳解提升5%以上,SA算法解的四分位数范围和总范围都是CIPBS的2倍以上,说明CIPBS算法的解更加集中,即CIBPS算法可以获得更有效的稳定解决方案.在场景b(用例4~6)中,即使解空间相比于场景a更小,即使此时的SA的解范围更加集中,CIBPS的性能提升反而更加明显,原因是此时任务目标点的分布更加集中,任务时间窗口间的冲突更大,CIBPS通过计算成像概率进行预测,化解任务间的冲突,可以取得更好的效果.在场景c(用例7~15)中,CIBPS和SA的解分布接近场景a,CIBPS的解非常稳定,四分位数范围和总范围都明显小于SA. 总的来说,CIBPS几乎在每种情况下都能找到更好的任务调度解.由此可以得出结论,CIBPS算法在性能方面明显优于SA算法,CIBPS算法在有效性和稳定性方面的优势是显而易见的. 本文深入研究了多卫星对地观测任务调度模型和调度算法,对多星观测调度问题进行约束性分析,确定了基本假设和约束条件,针对现有的确定性调度算法的性能退化、搜索算法易陷入局部最优、其它启发式算法规则制定不全面的问题,根据观测卫星的实际情况,提出了CIPBS算法,使规划结果尽可能接近最优解.在三种不同的任务分布下进行实验,通过调度结过分析对比表明本文提出的算法适应于多星预调度模型求解,能稳定的找到更好的解.但是本文还是存在一些不足,在对地观测任务完成后的卫星数据下传时间窗口分配未进行优化,如何结合CIBPS算法的特点设计观测卫星数据下传算法也是今后研究的方向.3.2 算法分析
4 实验与仿真
4.1 实验设置
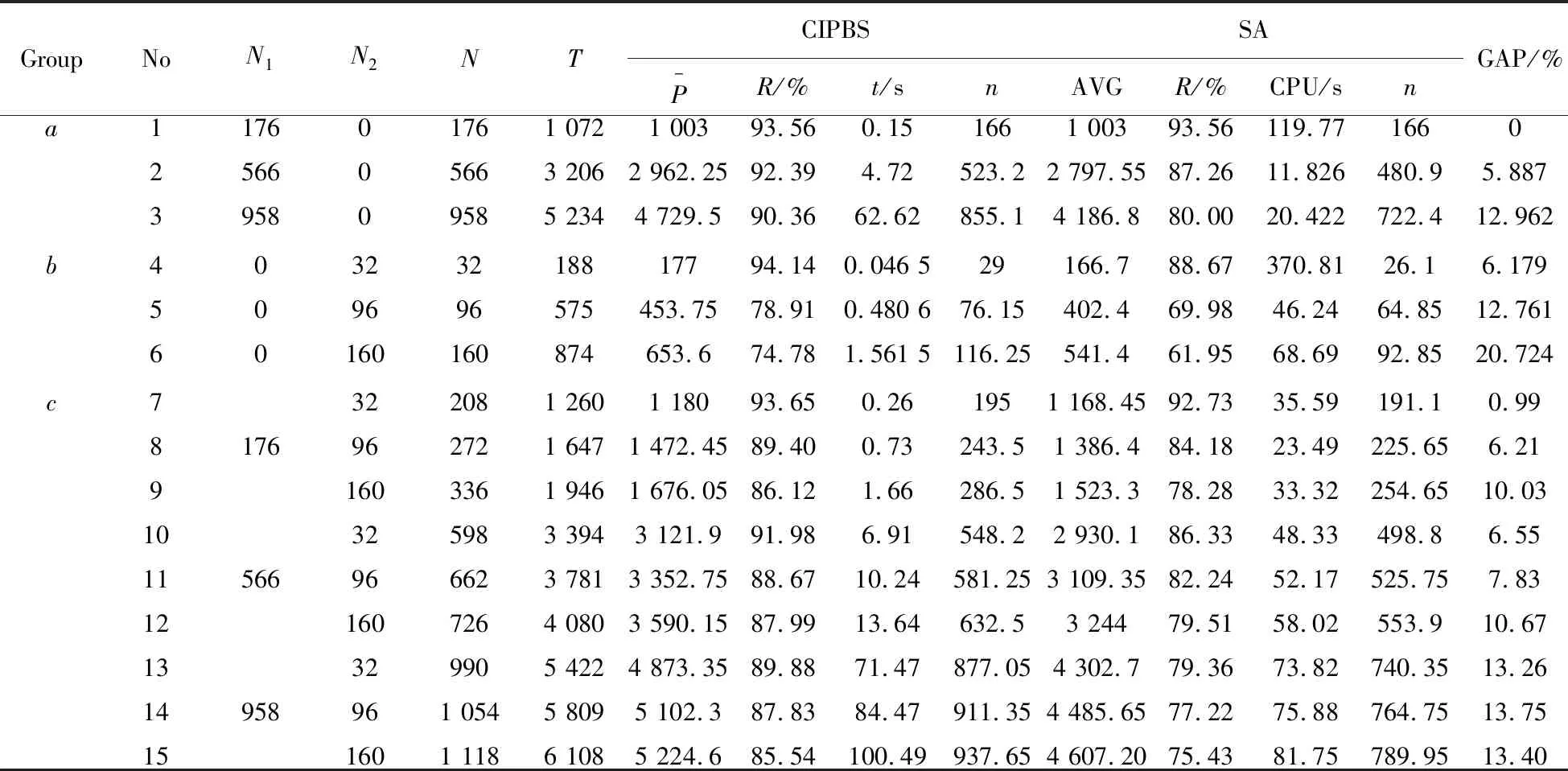
4.2 实验结果

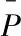
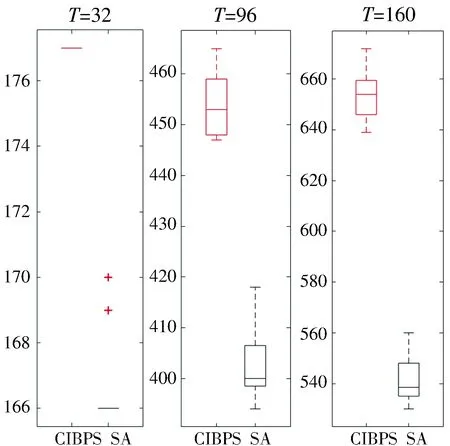
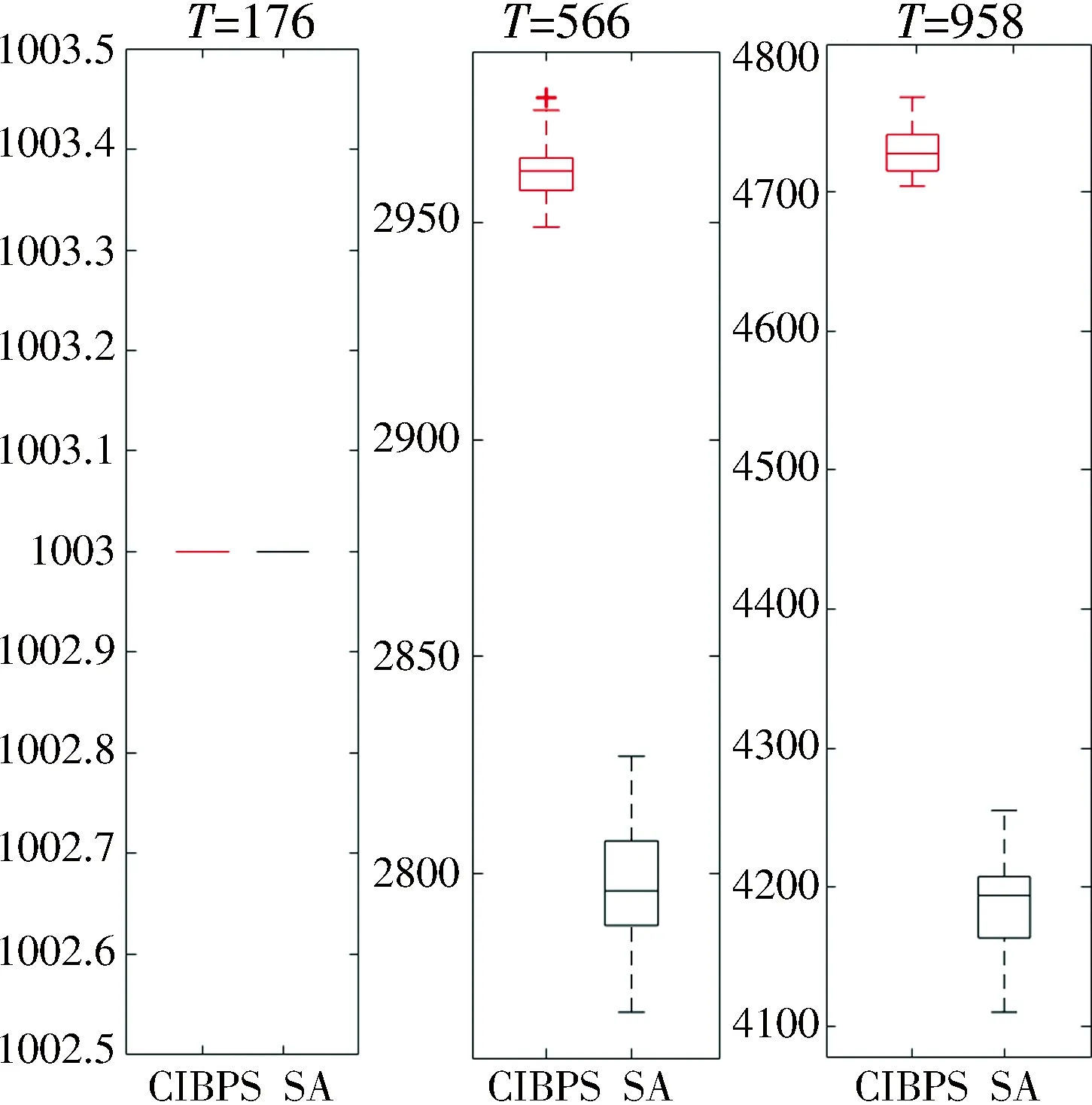
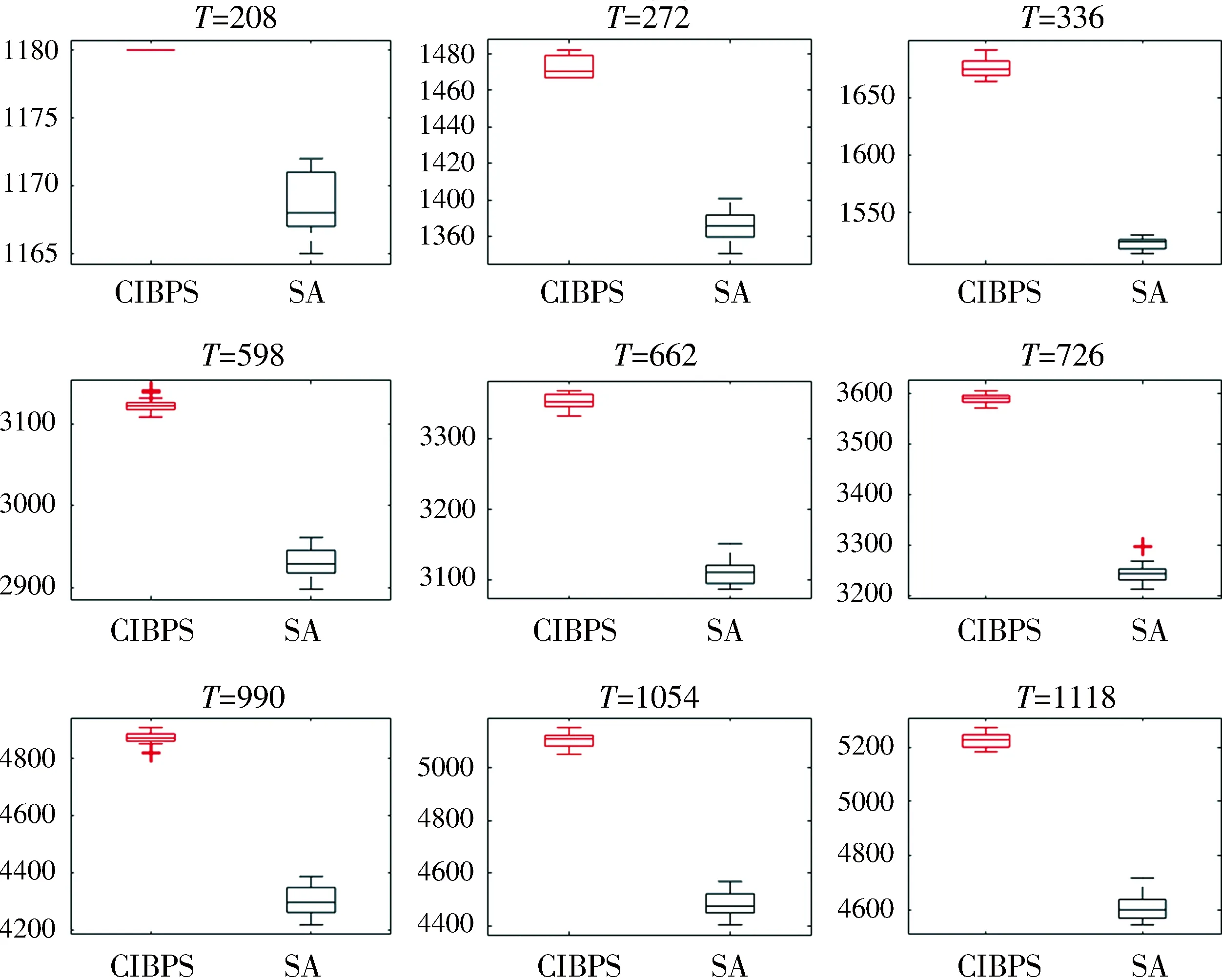
5 结 论
