一个包含目标趋向性的增强型Cucker-Smale群体运动模型

曾庆荣，李鹏飞，季袁冬，罗懋康,

(1.四川大学空天科学与工程学院，成都 610064； 2 四川大学数学学院，成都 610064)

1 引 言

群体运动的概念来自于鸽群、鱼群等生物群体的自组织行为.在群体内部，个体通过局部信息和简单作用规则即可达到整个群体运动状态一致，并表现出分布式、自适应、鲁棒性等特点.

通过对群体运动过程中个体的速度、位置以及个体间的相互作用进行描述，Vicsek等[1]首次建立数学模型描述了群体运动的形成机理.在此基础上，Cucker和Smale[2]提出了Cucker-Smale模型,该模型可以作为控制方案应用于无人机集群飞行及机器人编队控制等工程领域.传统的Cucker-Smale模型为[3]：

(1)

权函数

(2)

在文献[2-3]中，作者证明：当β<1/2时，群体内个体间的速度差将无条件收敛，群体内个体的运动状态达到一致；当β≥1/2时，这种收敛只在一定的群体初始条件下才成立.近年来，研究人员对Cucker-Smale模型提出了多种改进，以适应考虑噪声、时延及避免碰撞等应用场景.其中，Cucker和Dong等研究了受噪声和时延影响的改进模型，给出了发生群聚的阈值条件[4-7]，并提出了避免碰撞的模型，在原始模型中添加了一项排斥力[8].也有研究人员在文献[8]的基础上对避免碰撞的模型做了进一步的改进[9-15]，如Shen将等级制度引入模型，并研究其收敛结果[16].之后，研究人员又对加入了等级制度的模型进行了进一步的研究[17-18].另一方面，对于群体中个体间邻域问题的描述，Martin和Cucker等研究了引入拓扑作用邻域的Cucker-Smale模型，给出了发生群聚的条件[19-20].

在自然状态下，生物群体在运动过程中会整体性地朝向目标运动，即具有一定目标趋向性.同样，在工程应用中，无人机群或机器人群体也可能需要朝预定的目标运动.然而，目前各种Cucker-Smale群体模型虑及群体目的的较少，大多仅描述群体内所有个体问的“协调”，即群体内部所有个体协调一致地运动且未发生矛盾，而不考虑描述群体内所有个体的“协同”，即群体内部所有个体协调地实现一定的目的.本文将引入考虑了目标趋向性和几何邻域的Cucker-Smale增强模型及其效用评价效有函数，对该模型趋向群体目标的效用及目标趋向作用的引入对速度匹配等群体目标的影响进行仿真.

2 模 型

考虑速度匹配、避免碰撞、群体聚集及趋向目标这四个群体目标，我们建立如下模型：

(3)

其中xi和vi分别表示个体i在时刻t的位置和速度，x*表示群体目标的位置，Ν为群体个体构成的集合，Γi为个体i几何邻域内个体的集合，|Γi|为邻域集合内个体数目.

在式(3)中，加速度的第一项为速度匹配项，模型通过该项实现速度匹配的群体目的，其中权重aij(x)由(2)式定义.速度匹配项通过与邻域内其余个体的速度差来调整自身加速度，实现速度匹配.

加速度的第二项为个体间作用项，模型通过该项实现避免碰撞以及群体聚集的群体目的，其中个体作用函数f(‖Δxij‖)的定义为

‖Δxij‖=‖xi(t)-xj(t)‖为个体间距r，d0为群体个体间的最小安全距离，D0为排斥作用的最大距离，Γi为个体i几何邻域内个体的集合，Ωi为邻域外个体的集合.

个体作用函数可分为邻域内和邻域外两个部分.当邻域内个体间距d0D0时，个体受到吸引作用，个体间距越大，吸引作用越强.此外，处于个体i邻域外的个体对其有微弱的吸引作用，以避免“分群”现象的发生.

加速度的第三项为目标趋向作用项，模型通过该项实现趋向目标的群体目的，其中的吸引作用函数g(‖x*-xi(t)‖)定义为

g(r)=k4r-α

(5)

其中α>0为比例系数，调整α的大小可以调整目标趋向作用函数的形状，k4为目标趋向作用权重系数，调整k4的大小可以描述不同强度的目标趋向作用.目标趋向作用项通过将“引力”势函数加入到群体内单个个体的加速度项中，使得群体的运动受到一个整体的牵引作用，以描述群体运动趋向预定目标的目的.

为定量分析模型效能，我们需要建立效能函数.为实现速度匹配、群体聚集、避免碰撞及趋向目标这四个目标，在不同初始条件以及不同参数设置下，模型对几个群体目的的实现情况各不相同.

下面我们给出速度匹配差、群体离散度、碰撞个体数及目标偏离角等四个指标：

ψ3=Ncrash,

ψ4=arg(vcg,x0-xcg)，

其中，N为群体内个体数目，Ncrash为碰撞个体数目，x0为群体目标点的位置，vcg为群体的重心速度，xcg为群体重心位置，定义为

(6)

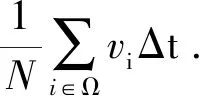
速度匹配差ψ1刻画了运动过程中群体速度的匹配程度，取值越小说明群体速度匹配程度越高，ψ1=0即意味着群体速度实现了完全匹配.

群体离散度ψ2刻画了运动过程中群体的聚合程度，取值越小意味着个体间距越小，群体聚集效果越好.如果群体最终达到稳定状态，则群体离散度变化曲线收敛到某一稳定值.

碰撞个体数ψ3为群体运动过程中发生碰撞的个体数量.当碰撞个体数为0时，群体就达到了避免碰撞的目的.

目标偏离角指标ψ4刻画了群体趋向目标的程度，其取值越接近0意味着群体朝向目标的误差越小.

3 仿 真

仿真的初始条件设置为：群体内个体数为100，均匀随机分布在200 m×200 m的平面空间内；每个个体初始速度大小范围为10～20 m/s，初始速度方向分布范围为-45°～45°；群体目标点设置为距群体初始分布中心10 km处；群体内个体间最小间距为3 m，个体间距离小于3 m视为发生了碰撞.在仿真中，群体模型内除目标趋向作用权重之外的各项参数设置为：速度匹配权函数参数H=100，β=0.4；邻域内作用函数参数k1=1 000，k2=200，θ1=θ2=0.1；邻域外作用函数参数k3=0.5，θ3=0.3；目标趋向作用函数参数α=0.1.在所有仿真中，时长均为100 s.为避免随机初始分布对结果造成影响，每次仿真均随机取值重复进行200次取平均值.

图1给出了不同k4取值下和2～12 s时间段内的目标偏离角函数，以及k4从1到100变化时目标偏离角函数最后10 s的收敛均值.

图1 不同目标趋向作用权重下的目标偏离角曲线(a) 目标偏离角曲线；(b)目标偏离角曲线的局部放大； (c) 目标偏离角曲线的最终收敛值Fig.1 Target deviation angle curve at different weight of target directed interaction(a) The target deviation angle curve; (b) partiall enlarged view of the target deviation angle curve; (c) finall convergence value of the target deviation angle

表1 不同目标趋向作用权重下的碰撞个体数以及群体稳定时间Tab.1 Collision number and group stability time at different weight of target directed interaction

图1(a)显示，在各项目标趋向作用权重下，目标偏离角整体上有明显的收敛趋势.当k4大于一定值时，在群体运动了40 s左右时群体的目标偏离角均收敛到0附近.这说明群体在一定目标趋向作用权重下已实现了趋向目标的群体目的.同时，从图1(b)可以看出，随着目标趋向作用权重的增加，群目标偏离角的收敛速度加快.从图1(c)可以看出，随着目标趋向作用权重的增加，目标偏离角指标的最终收敛值逐渐减小.当目标趋向作用权重大于30时，该指标的最终值下降至0附近.这说明当目标趋向作用权重越大时，趋向目标的群体目的效果越好.

我们通过仿真得到碰撞个体数，速度匹配差，群体离散度及群体稳定时间等，进而分析引入了目标趋向作用权重之后的影响.

表1给出了当目标趋向作用权重k4在10到100范围内碰撞个体数指标以及群体稳定时间的变化，其中稳定时间定义为当群体的速度匹配差指标下降至一定阈值条件以下时所需的时间.这里我们取阈值为0.1.可以看出，在各个权重下群体在运动过程中均没有发生碰撞.这说明目标趋向作用的引入对于群体内部避撞的功能没有影响.随着目标趋向作用权重的增大，群体的稳定时间呈现出先减小后增大的趋势.当权重较小即k4<40时，群体在仿真的100 s时长内均没有达到群体稳定时所需的阈值条件.当权重4060时，由于离散仿真有可能造成在一个步长内个体会受到过大的目标吸引力而调整过大，进而使得个体在一个步长内来回抖动，导致稳定时间随着权重的增加而增大，因而目标趋向作用权重也不宜取得过大.群体要达到一致状态，首先要使群体的速度匹配差指标在一定时间内下降至阈值以下，即达到稳定状态.因此，群体稳定时间的要求需要优先判断.在稳定时间满足要求的前提下再考虑群体离散度以及目标偏离角的需求.从表1中可以得到，群体的目标趋向作用权重应大于30才能在规定时间内达到稳定状态.

图2显示了不同k4取值下速度匹配差随时间的变化以及k4在1到100范围内速度匹配指标最终的收敛均值.

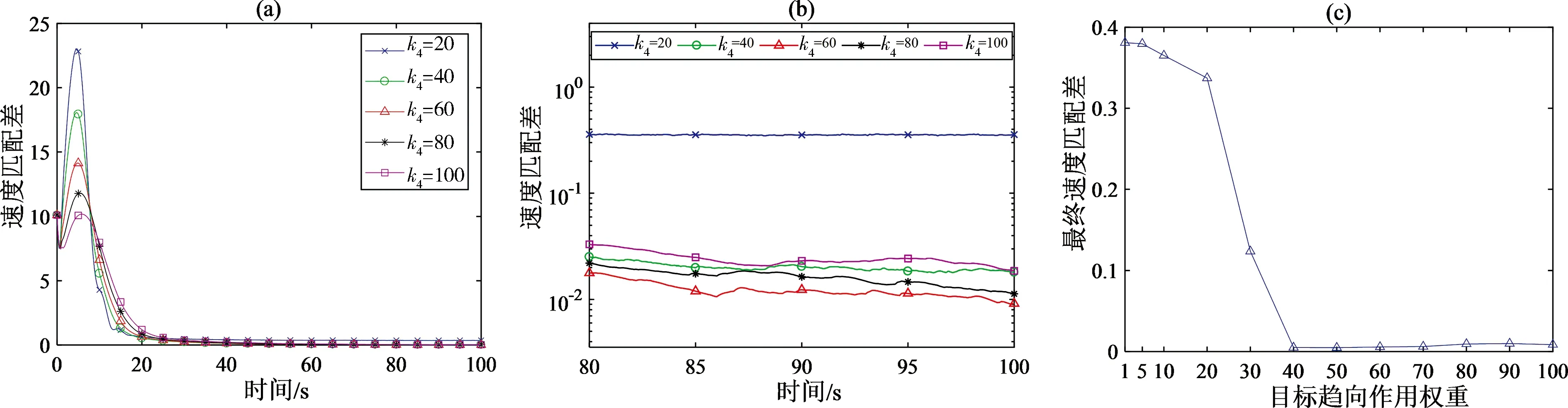
图2 不同目标趋向作用权重下的速度匹配差曲线(a) 速度匹配差曲线；(b) 曲线的局部放大； (c) 速度匹配差的最终收敛值曲线Fig.2 Speed matching difference curve at different weight of target directed interaction

(a) Speed matching difference curve; (b) partially enlarged view of the speed matching difference curve; (c) finally convergence value of the speed matching difference curve

图2(a)显示，在各项目标趋向作用权重下群体的速度匹配差均有明显收敛到0附近的过程.这说明群体均能很快实现内部个体间速度的一致.同时，在运动过程中速度匹配差指标有一个明显的波动.这是因为在群体运动初期，群体前端的个体会受到吸引作用而先有一个减速的效果，使得速度匹配差增大，之后再由于速度匹配作用而减小.由于目标趋向作用会阻碍群体内个体间的吸引作用，我们可以看到，随着目标趋向作用权重的增加，速度匹配差曲线的波动越小，从而更容易实现群体内个体间速度的一致.从图2(b)可以看到,当k4不同取值时，速度匹配差最终收敛值也不同.从图2(c)可以看到在1到100范围内，随着权重的增加，速度匹配指标的最终收敛值逐渐减小.当权重大于30时，该指标的最终值下降至0附近.这说明目标趋向作用对模型速度匹配群体目的的实现具有正向的促进作用.当k4继续增大时，由于单步长内速度调整过大而出现的抖动使得速度匹配差随着k4的增大而有微弱的增加.这表明群体目标吸引项对于群体速度的匹配具有积极的效果.

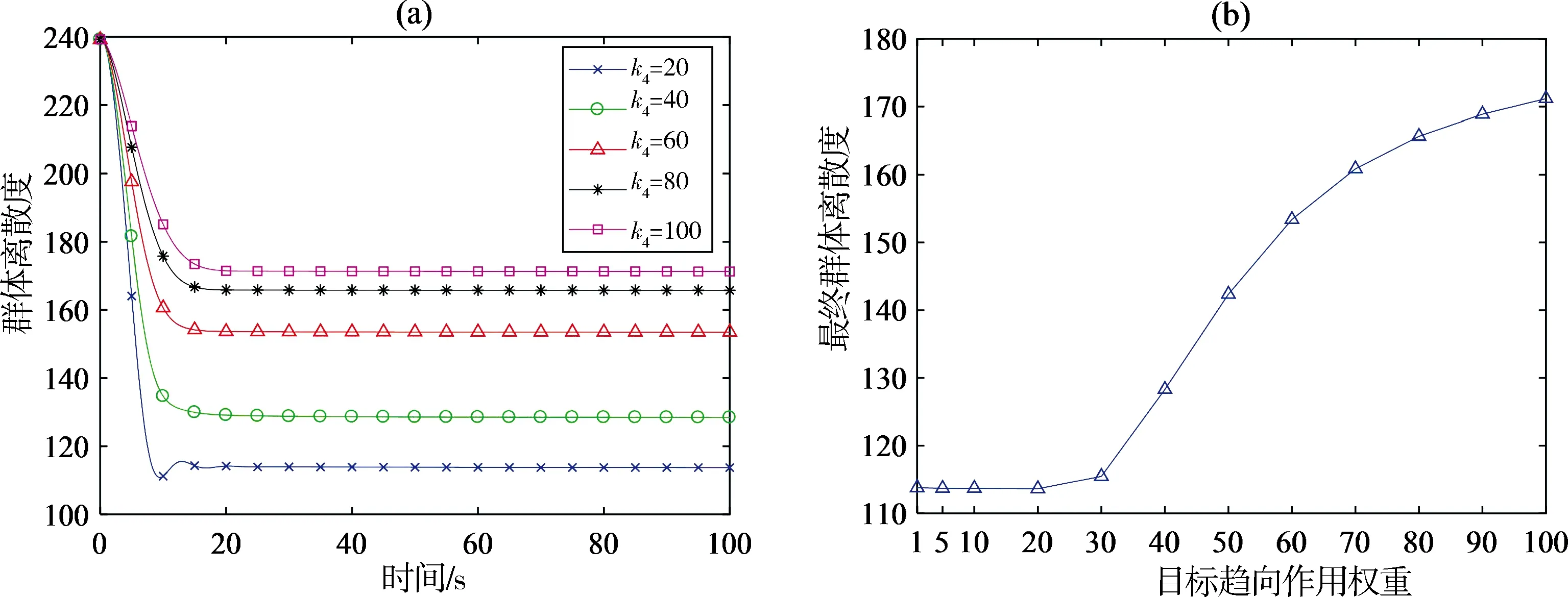
图3 不同目标趋向作用权重下的群体离散度曲线(a) 群体离散度随曲线；(b) 群体离散度最终收敛值曲线Fig.3 Group dispersion degree curve at different weight of target directed interaction(a) Group dispersion degree curve; (b) finally convergence value of the group dispersion degree

图3为在目标趋向作用权重k4不同取值下群体离散度的时间变化及k4在1到100范围内群体离散指标最终的收敛均值.由图3(a)可见，在各项权重下，群体离散度指标均有一个收敛的过程，群体在运动过程中均能够实现聚集.同时，随着权重的增加，群体离散度的收敛值逐渐增大.这是因为，权重越大群体在运动过程中受到的目标趋向作用越强，从而使得群体内部个体间的吸引作用越弱，更难实现群体的聚集.从图3(b)可以看到，随着k4的增加，群体离散指标的最终收敛值逐渐增大.这说明目标趋向作用的增加不利于模型群体聚集目的的实现.根据前文群体稳定时间的仿真结果，群体的目标趋向作用权重应大于30才能在仿真时长内达到稳定状态.因此，在设定的初始条件下，在满足群体稳定时间要求的前提下群体离散度指标最优值应在k4=40附近取得，这里为128.31左右.

综上所述，引入了目标趋向力以及几何邻域并不影响避免碰撞、速度匹配及群体聚集这3个群体目的的实现，并且当目标趋向作用权重增加时，群体最终的速度匹配差均值减小，群体能够更快地达到稳定状态.然而，目标趋向作用的增加会阻碍群体的聚集，使得群体离散度增大.在满足群体稳定时间的要求下，我们可以根据群体目标偏离角和群体离散度是否达到预期的阈值条件来判断两个群体目的的实现情况.在本文设置的初始条件下，我们可以设目标偏离角阈值为0.1，当目标偏离角在一定时间之后小于0.1则视为达到了趋向目标，另一方面，我们可设置群体离散度指标阈值为150，当群体离散度收敛值小于150时视为达到了群体聚集.在满足阈值条件的情况下，选择稳定时间最小的目标趋向作用权重k4=40.在实际应用中，目标偏离角和群体离散度两个指标的阈值可根据群体初始条件设置以及实际需求设定.

4 结 论

在本文中，我们将目标趋向作用和几何邻域引入Cucker-Smale群体模型，得到了一个增强型群体运动模型.该模型能够实现速度匹配、避免碰撞、群体聚集及趋向目标等4个群体目标.仿真结果表明，当目标趋向作用权重增加时，群体趋向目标运动的速度和程度均会增加，同时对群体内个体速度的匹配有积极促进作用，对群体的聚集则有消极影响.速度匹配作用对群体内个体加速度的影响与此类似，也会阻碍群体的聚集.此外，过大的目标趋向作用权重也会导致群体内个体在单步长内速度调整过大而发生抖动，进而使得稳定时间和速度匹配差收敛值变大.因此，群体模型的目标趋向作用权重不能过大也不能过小，需要根据群体的初始状态以及群体所处环境给出合理值.