抛物型积分微分方程的新型全离散弱Galerkin有限元法
2020-09-23刘轩宇
刘轩宇,罗 鲲,王 皓
(四川大学数学学院,成都 610064)
1 引 言
考虑下面的抛物型积分微分方程:
其中Ω⊂Rd(d=2,3) 是一个有界凸多边形(多面体),其边界记为 ∂Ω.在物理和工程领域,同时带时间变量和空间变量的系统非常常见.在研究其中一些问题时,必须考虑之前的状态对现在状态的影响.抛物型积分微分方程应运而生.这类方程在热传导、核反应堆动力学、热弹性力学等领域有广泛的应用[1-24].针对这类方程,近几十年来出现了很多数值方法,如混合有限元方法[7,13,18],谱方法[8],全离散自适应有限元方法[17],间断Galerkin方法[14,15],最小二乘Galerkin方法[9],紧致的交替隐式差分格式[16]等.
弱Galerkin (Weak Galerkin,简称WG)有限元法是近几年发展起来的用于求解偏微分方程的一类有限元方法[25-29],最早由Wang和Ye针对二阶椭圆方程提出[21,23].WG方法通过引入对间断函数适用的弱微分(弱梯度,弱散度)算子,使相应变分方程容许间断的逼近函数.此方法既有间断有限元法网格剖分灵活的特点,也有局部消去的特性,减少了变量个数.近年来,WG方法更是被推广应用到多种偏微分方程的数值求解,如线弹性问题[3],Stokes方程[2,20,22,25,27],Ossen方程[12],Biot固结问题[5],对流扩散反应方程[1],重调和方程[1]等.
针对二维抛物型积分微分方程,文献[29]提出了一类WG有限元方法,给出了半离散格式与全离散格式的解的存在唯一性,导出了相应的误差估计结果.本文与该文献所提出的格式的不同之处在于:
·本文的分析同时适用于二维与三维情形;
·本文除了适用于单纯形网格,还适用于任意多边形(多面体)网格,文献[29]只针对二维的三角形网格;
·本文采用Crack-Nicolson格式,时间方向上精度为二阶,文献[29]对时间的离散采用了向后Euler差分格式,时间方向上精度为一阶.
本文的剩余内容安排如下: 第2节给出本文的记号和预备性结果;第3节给出半离散格式以及相应的误差估计;第4节给出了全离散格式以及相应的误差分析;第5节给出数值结果.
2 预备知识
2.1 记号

引入空间
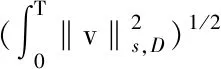
L(0,T;Hs(D)):={v:(0,T]→Hs(D),v是可测函数,且<}
及相应的范数

‖u‖L(0,T;Hs(D))
在本文中,除特殊说明外,我们用C表示与网格尺度h和时间步长Δt(稍后定义)无关的正常数.
2.2 预备结果
Gronwall不等式: 设u(t),β(t),α(t)是定义在区间[a,b]上的实值连续函数,其中β(t)≥0对任意t∈[a,b],若
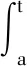
则有
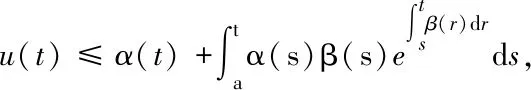
∀t∈[a,b]
(2)
离散的Gronwall不等式: 设(kn)n≥0,(pn)n≥0均为非负数列.若数列(φn)n≥0满足
则
(3)
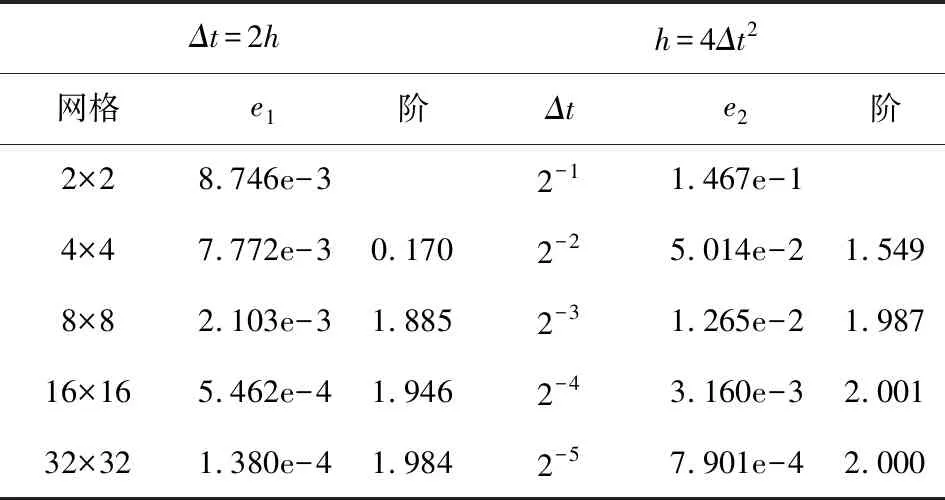
右矩形公式误差估计: 设实数a,b满足a (4) 梯形公式误差估计: 设实数a,b满足a (5) 则 (6) 根据文献[21],我们来定义离散的弱梯度算子.给定Ω上的一个划分Th,对于T∈Th,用V(T)表示T上的弱函数空间,其定义如下: V(T)={v={v0,vb}:v0∈L2(T), vb∈H1/2(∂T)} (7) 选择一个有限维向量空间G(T)⊂H(div,T),定义离散弱算子w,G,T:V(T)→G(T). 定义3.1对于任意的v∈V(T),相应的离散弱梯度算子w,G,Tv∈G(T) 满足下列方程: 〈vb,τ·nT〉∂T∀τ∈G(T) (8) 特别地,如果G(T)=[Pr(T)]d,我们直接记w,rw,G. vhb|e∈Pk-1(e),∀T∈Th,∀e∈εh}, (9) 初值条件为uh(x,0)=Ehu0(定义见后文式(29)),这里 a(uh,vh)=(w,k-1uh,w,k-1vh), as(uh,vh)=a(uh,vh)+s(uh,vh). 我们引入一种半范数:对于任意vh∈Vh,定义 ‖|vh|‖2:=as(uh,uh)=‖wvh‖2+ (10) 引理3.2[21]对于qh={vh0,vhb}∈Vh,T∈Th,wvh=0 在T上成立当且仅当vh0=vhb=常数. 引理3.3[3]设整数m满足1≤m≤j+1.则对于任意T∈Th,e∈∈h,有 ∀v∈Hm(T), ∀v∈Hm(T),0≤s≤m, ∀v∈Hm(T),0≤s+1≤m. 设uh0(t)|T=Φ0α(t),uhb(t)|T=Φbβ(t),wuh(t)|T=Φγ(t),其中给出一些矩阵的定义如下: 在式(8)中取τ=φj,j=1,2…r3,可得 (11) (12) 在式(9)中取vh={0,vhb}={0,φjb},j=1,2…r2,可得 (13) 设 则 (14) (15) (16) (17) (18) 其中, 在方程(17)和(18)两端对时间变量求导,则有 设 0≤t≤T, (19) 引理3.5[28]设u∈L(0,T;Hk+1(Ω))为问题(1)的真解. 记ρ{ρ0,ρb}=Ehu-Qhu.则当h足够小时,有 注1文献[28]中只证明了二维RT元的情形.事实上,对(k,k-1,k-1)型元以及三维的情况可类似证明. 对(19)两边关于t求导,再由类似引理3.5的方式我们可以得到ρt,ρtt的估计如下. 引理3.6假设引理3.5的条件均成立,且ut∈L(0,T;Hk+1(Ω)),则当h足够小时,有 进一步,若utt∈L(0,T;Hk+1(Ω)),则当h足够小时,有 引理3.7[21]假设v∈Hk+1(Ω),其中k≥1.则‖v-w(Qhv)‖≤Chk‖v‖k+1,其中 (20) (21) (22) 由Ehu的定义可知 (23) 结合(9),(22)和(23)式可得 ((ξ0)t,vh0)+as(ξ,vh)= (24) 取vh=ξt.由于 则 (25) 对时间变量从0到t积分,考虑到ξ(x,0)=0,则有 (26) 对于右端第二项,由分部积分公式可得 结合‖|·|‖的定义,有 利用Gronwall不等式,结合引理3.6,可得如下结果: 则式(20)可通过引理3.5,引理3.7和三角不等式得到. 在式(24)中取v=ξ,有 C‖(ρ0)t‖2+‖ξ0‖2+ 易得 对时间变量从0到t积分,可得 利用Gronwall不等式,考虑到ξ(x,0)=0,结合引理3.5,可得如下结果 结合引理3.5,引理3.4和三角不等式,我们得出式(21).证毕. vh)=(f(·,tn+1/2),vh0) (27) 定理4.1问题(1)的的全离散格式(27)有唯一解. 在开始分析误差之前,我们先给出一些逼近误差的定义和估计.当n=0,1…N-1时,记 Eh0ut(·,tn+1/2). 当n=1,2…,N-1时,记 (28) (29) (30) (31) 根据Eh0u(·,tn+1)和Eh0u(·,tn)在tn+1/2处的Taylor展开式,可得 由复合梯形公式(7)和右矩形公式(4)的误差估计,得 由梯形公式的误差估计(5),有 (32) 由引理3.6,引理3.4,3.7和三角不等式,可得 (33) 类似可得 进而可得出式(28)~(31). 注2证明过程中利用到了时间与空间的独立性,即(wEhu)tt=wEhutt,(wEhu)t=wEhut,(Eh0u)tt=Eh0utt. 定理4.3设u是问题(1)的解,且满足u∈L(0,T;Hk+1(Ω)),utt1,2…N)是全离散格式(26)的解,则h足够小时,有 (34) (35) 证明 记 Qhu(x,tn+1/2),n=0,1…,N-1. (36) 在式(36)中取t=tn+1/2,结合式(27),(19),可得 (37) 取vh=ξn+1+ξn.我们有 (38) 其中 对于式(38)左端第一项,通过计算可得 (39) 下面估计式(38)的右端项.利用Young不等式,有 (40) (41) 利用Young不等式,可得 进而有 (42) 结合式(38)~(42)以及|‖·‖|的定义,可得 上式两边同时乘上Δt,对n从0 取到m-1求和,由 再结合ξ0=0可得 其中 利用离散的Gronwall不等式可得 由引理3.5可得 再结合引理4.2有 结合引理3.5,引理3.7与三角不等式,我们得出式(34). 在式(37)中取vh=∂tξn+1.对于 0≤n≤N-1,有 (43) 其中 对于方程(43)的左端项,有 as(ξn+1+ξn,ξn+1-ξn)=|‖wξn+1‖|2- (44) 对于其右端项,我们有 (45) 同时,由 (46) 结合式(43)~(45)可得 (47) 上式对n从 0 取到m-1求和,再两边同时乘Δt,可得 (48) 现分别估计上式右端的三项.我们有 对于第三项,采用与式(42)同样方式可得 因此 (49) 结合式(48),(49)和 |‖·‖|的定义,有 其中 利用离散的 Gronwall 不等式,可得 由引理3.5和引理4.2,我们有 Hk+1(Ω))]. 最后,根据引理3.5,引理3.4和三角不等式,即得式(35).证毕. 本节将用数值算例来验证定理4.3中的理论结果.在所有算例中,取Ω=(0,1)×(0,1),T=1,选择右端项f使初值条件使真解为u(x,t)=t2x1(1-x1)x2(1-x2). 由表1和表2可以看出,k=1时,u的逼近在时间精度上有2阶,在空间精度上有2阶,与定理4.3相符;u的逼近在时间精度上有2阶,在空间精度上有1阶,也与定理4.3相符. 表1 正方形网格,k=1Tab.1 Squaredgnid,k=1 表2 正方形网格,k=1Tab.2 Squaredgnid,k=1
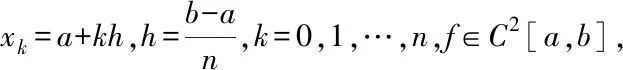
3 半离散WG有限元方法
3.1 网格剖分


3.2 离散弱算子
3.3 半离散格式
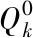

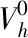

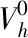



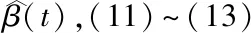



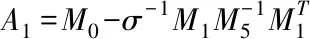
3.4 误差估计


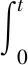



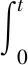
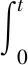




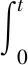

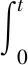
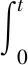

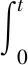


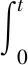


4 全离散WG有限元方法
4.1 全离散格式



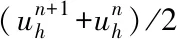
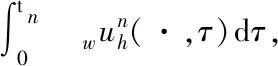

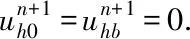
4.2 误差估计
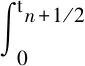
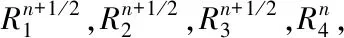





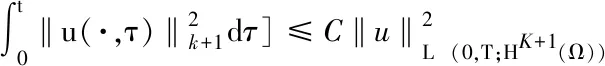
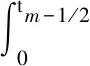
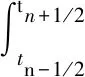


5 数值实验