拟静力Sarma法在岩质边坡稳定性分析中的应用

2020-09-22王紫杰

工程技术研究 2020年16期

王紫杰

（重庆大学土木工程学院，重庆 400045）

根据学者对汶川地震作用下岩质边坡的滑动破坏结构特征分析得出，在高强度地震作用下，滑体前缘为剪切破坏，后缘主要为拉破坏[1-3]。由此可见，高烈度地震作用下，高边坡滑体滑面为非光滑折线，因此分析高烈度地震作用下岩质边坡的稳定性使用拟静力Sarma法更加适宜。

1 拟静力Sarma法

拟静力Sarma法基本原理是边坡破坏的滑体并非是沿一个理想的平面或弧面滑动，才可能发生滑动。也就是说在滑体内部要发生剪切情况下才可能滑动，该方法适合高强度震区边坡的稳定性计算。将岩质边坡划分为若干滑块，块间接触面为倾斜面，第i块受力分析如图1所示。

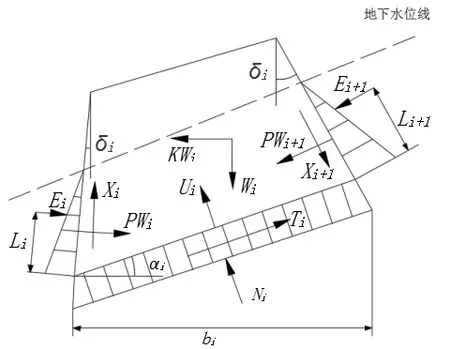
图1 Sarma法计算简图

根据条块垂直和水平方向力的平衡，可以得到：

根据Mohr-Coulomb破坏准则，在底面和左、右界面有

将式（3）～式（5）代入式（1）和式（2）消去Ti、Xi、Xi+1和Ni可以得到：

式（6）是个循环式，可以得到：

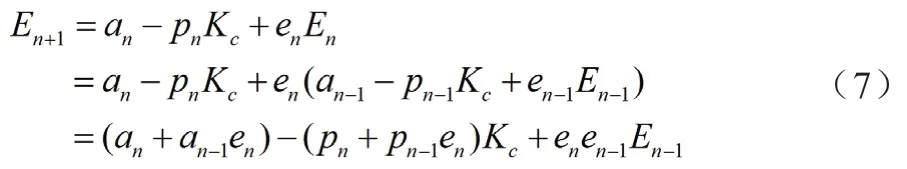
进一步得到：

计算Kc。假设没有外荷载作用，则En+1=E1=0可以得到：

式中：i为块体号；E、X分别为作用于条块界面的法向力和切向力；αi为第i块体的条块底面与水平面的夹角；为条块左侧界面的平均内摩擦角；为条块底面的平均内摩擦角；δi表示条块左侧界面与垂直方向的夹角，以铅直线为起始线，顺时针为正，逆时针为负；Wi为第i块体的重力；为条块左侧界面的平均粘聚力；ci为条块底面平均粘聚力；bi为条块底面宽度；di为条块左侧界面的长度；K为加速度系数；不考虑孔隙水压力和渗透压力，Ui为作用在条块底面上的水压力，PWi为作用在条块界面上的水压力。

计算安全系数时，假定安全系数为某个值k，以ci/k代替ci，，通过用迭代法根据公式（9）计算k和所有未知数。

地震作用下加速度系数K由以下公式计算：

式中，amax为坡体实际所受地震加速度最大值；g为重力加速度；γ0为地震效应折减系数，一般取0.25，C为动力分布系数。

2 例题计算

2.1 例题

文章以某岩质边坡工程实例作为计算分析的模型，边坡的岩体参数和剖面结构等数据均来自地质勘察资料。本例先通过AutoCAD对边坡的剖面进行处理，划分岩质土体所在的范围，然后导入ANSYS软件中进行三维建模和网格划分，最后再将划分好的三维模型导入FLAC3D进行数值模拟计算，最后得到的数值计算模型如图2所示。

图2 FLAC3D计算模型

数值模拟采用Mohr-Coulomb塑性本构模型进行计算，岩土体强度相关参数采用平均值作为标准值，岩体详细参数如表2所示。

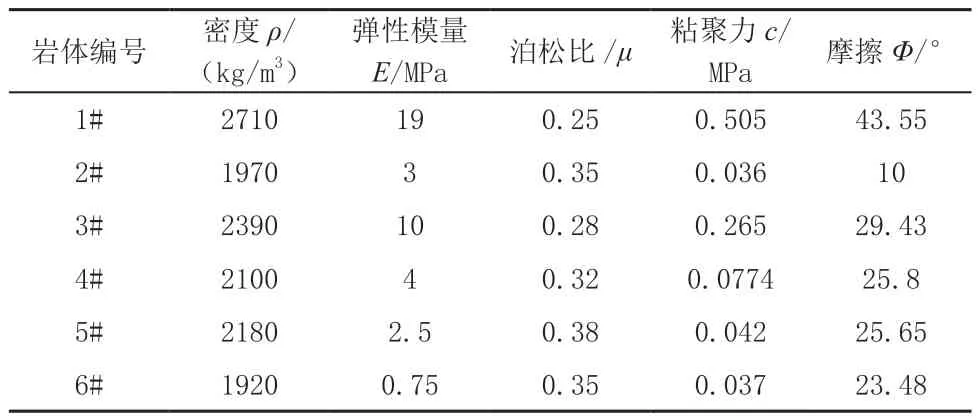
表2 岩体物理学参数

2.2 计算过程

以FLAC3D数值模拟计算安全系数时得到的边坡的位移变量云图所确定的滑面作为边坡动力Sarma法计算的潜在滑移面，将岩边坡进行简化分块，建立计算模型如图3所示。

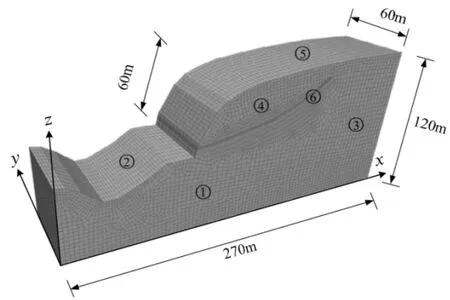
图3 动力Samra法计算模型

各块体力学性质及岩质参数使用加权平均值作为计算值，地震波选取著名的埃尔森特罗波，C取1，计算得出地震加速度系数K=0.0852，带入公式计算得出边坡动力安全系数为1.02。FLAC3D数值模拟计算得到的安全系数值为1.01。由此可见，该边坡使用拟静力Sarma法计算得出的动力安全系数与FLAC3D数值模拟计算得出的安全系数接近。