风机用集成式机液伺服阀芯配合间隙的流场分析*

贾永帅,苏东海

(沈阳工业大学 机械工程学院，辽宁 沈阳 110870)

0 引 言

风机风量调整机构是锅炉鼓风机、引风机系统主要部件之一，其基本原理是通过机液伺服系统来推动风机叶片，使其转变一定的角度，从而达到风机风量调节的目的[1]。因此，集成式机液伺服液压缸的性能直接影响到风机的正常工作质量。机液伺服阀是集成式机液伺服液压缸的主要部件，伺服阀的性能好坏对集成式机液伺服液压缸的动态性能优劣起决定性作用。

由于机液伺服阀需要跟随风机叶片以1 500 r/min的高速旋转，其在实际工作中容易产生阀芯卡滞、泄漏量大等现象，这会严重影响风机正常工作，所以对其伺服阀阀芯间隙流场的特性研究就显得尤为重要。

秦明璋等[2]从伺服阀面积梯度等方面对集成式机液伺服液压缸响应特性进行了研究，但对集成式伺服阀芯流场特性对系统动态性能的影响研究甚少。罗艳蕾等[3]对带锥度的阀芯圆环缝隙流动情况进行了分析，其大部分只针对滑阀静止情况下的间隙流动状况的研究，结论具有一定局限性，无法用于高速旋转风机用机液伺服阀的设计与优化。

笔者主要通过仿真分析风机用机液伺服阀芯偏心量[4]变化，以及锥度[4]改变对阀芯流场径向力[5]和泄漏量的影响，并通过建立系统数学模型分析验证仿真结果的正确性，为风机风量调整集成式机液伺服液压缸结构优化奠定基础。

1 模型建立及仿真条件设定

1.1 集成式机液伺服液压缸结构及原理

风机风量调集成式整集成式机液伺服缸结构如图1所示。

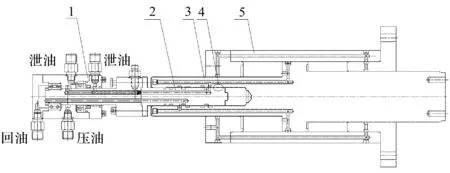
图1 集成式机液伺服液压缸结构图1—高速旋转接头；2—机液伺服阀芯；3—机液伺服阀套；4—阀芯环形间隙；5—液压缸

在机液伺服缸工作过程中，其通过高速旋转接头1将压力油配送给旋转过程中的伺服阀芯2、伺服阀套3以及液压缸5，经由伺服阀的调节，实现高速旋转中的机液伺服缸的动作，从而完成风机叶片角度调节。

该集成式机液伺服液压缸采用轴向配油方式以保证其在高速旋转中能够正常工作，集成式机液伺服液压缸中开设有多条泄漏油通道，能够很好地将高速旋转中的伺服液压缸的泄漏油引回油箱。

1.2 阀芯环形缝隙泄漏量与压力计算

通过分析可知阀芯环形间隙模型如图2所示。

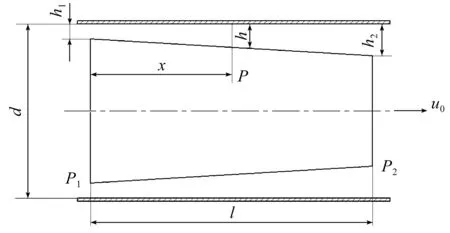
图2 阀芯环形间隙模型

阀芯为倒锥时对伺服阀的特性影响较大，所以笔者针对阀芯为倒锥的形式进行深入研究。

经推导，可得阀芯环形间隙泄漏量计算公式为：

(1)

式中：u0—阀芯移动速度；h1—进口缝隙；h2—出口缝隙；P1—阀芯缝隙进口压力；P2—阀芯缝隙出口压力；μ—油液粘度；d—阀套内径；l—环形密封间隙长度。

当阀芯静止时，即阀芯移动速度u0=0，可得伺服阀芯间隙中压力分布计算公式为：

(2)

式中：h—距离左端面x距离处的缝隙；P—距离左端面x距离处的压力。

式(1，2)只能大致估算阀芯缝隙泄漏量与压力分布情况，且该机液伺服阀以1 500 r/min高速旋转，这会导致阀芯间隙泄漏量与压力分布发生较大变化，因此，无法用公式计算来判断风机的机液伺服阀芯实际工作的泄漏状况，需要对风机用机液伺服阀芯缝隙流动状况进行仿真分析。

1.3 机液伺服阀阀芯间隙流场模型

由于在偏心方向上、下两侧表面流场是相互对称分布的，为了在不影响计算结果的情况下降低计算量，便于仿真[6]，阀芯间隙流场模型只需建立半个环形间隙即可。模型参数为：阀芯与阀套间隙为0.015 mm，模型长度l为25.5 mm，阀套内径d为32 mm。该模型共划分4 855 572个单元网格。

该阀芯模型较为简单，运用SIMPLE算法即可以得到收敛解，设置阀芯流场仿真的迭代残差为10-9。

1.4 控制方程

CFD的流场数值仿真需要满足质量守恒、动量守恒、能量守恒的流体力学三大守恒方程，基于三大守恒方程可以建立阀芯环形间隙流场数学模型。

阀芯环形间隙流场中介质流动的质量守恒方程为：

(3)

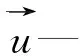
(4)

阀芯环形间隙流场中介质流动的动量守恒方程为：

(5)

式中：Fx,Fy,Fz—流体的体积力在x,y,z3个方向上的分量；p—流体微元体上的压力；τ—流体微元体表面的粘性应力。

由能量守恒定律可知，伺服阀芯环形间隙内介质的能量守恒方程为：

(6)

式中：ρ—流体密度；cp—流体的比热容；T—环境温度；k—流体的传热系数；ST—流体的内热源以及由于粘性作用流体机械能转换成热能的部分[7]。

1.5 仿真条件设定

由于机液伺服阀整体以角速度1 500 r/min高速旋转，其接触的边界内外壁面以及内流体模型均设置为以角速度158 rad/s转速旋转。

根据其实际工作状况，笔者选取阀芯间隙入口边界压力为12 MPa，出口边界压力为大气压力；设置流体密度ρ为870 kg/m3，动力粘度μ为0.04 Pa·s；流体采用不可压缩的牛顿流体[8]。虽然模型的内外壁面均以1 500 r/min高速旋转，但其对模型间隙流场的轴向流速几乎无影响。

由于环形缝隙很小，其液流速度将会很小。依据液体雷诺数方程[9]:

(7)

式中：ρ—介质密度，kg/m3；μ—介质动力粘度，Pa·s；D—阀套内径，m；d—阀芯直径，m；v—流体介质流动速度，m/s。

由式(7)计算可知，其雷诺数远小于偏心环缝临界雷诺数Recr，因此采取层流模型对阀芯间隙流场进行仿真分析。

2 伺服阀芯间隙流场仿真结果与分析

2.1 阀芯偏心量对间隙流场的影响

在阀芯为倒锥、倒锥半径差(锥台状阀芯的上下端面半径差)为0.01 mm以及阀芯与阀套间隙为0.015 mm(阀芯无锥度时的平均配合间隙)的情况下，通过改变阀芯偏心量分别为0.002 mm、0.006 mm、0.010 mm和0.014 mm，可以得出阀芯变偏心量的间隙流场云图，如图3所示。

图3 阀芯变偏心量的间隙流场云图

由图3可知：随着阀芯偏心量的增加，偏心侧的压力降明显加快，偏心侧与背离偏心侧压力差显著增加，这将导致阀芯两侧压力分布不均；随着压差的增加，阀芯径向力逐渐增加，阀芯将趋向偏心侧运动，最终导致阀芯卡滞，严重影响伺服阀的动态性能。

为了确保控制系统的动态性能，要求液压滑阀间隙的最大泄漏量不超过其额定流量的1%[10]。该伺服滑阀的工作流量为5 000 ml/min，故要求伺服阀间隙的泄漏量不得大于50 ml/min。

在给定的边界条件下，笔者通过对不同偏心量的阀芯间隙流场进行仿真，得出阀芯间隙的泄漏量，如表1所示。

表1 阀芯不同偏心量的间隙泄漏量

从表1中可以看出：随着阀芯偏心量的增加，伺服阀的泄漏量在逐渐增大；当偏心量达到0.014 mm时，泄漏量为63.76 ml/min，大于额定最大泄漏量50 ml/min，此时伺服阀的动态性能会遭受破坏，影响其正常工作。

所以在伺服阀装配过程中，要尽量保证阀芯与阀套的间隙不得超过0.010 mm，以保证机液伺服阀的稳定、高效工作。

2.2 阀芯锥度对间隙流场的影响

在阀芯为倒锥、偏心量为0.010 mm以及阀芯与阀套间隙(阀芯无锥度时的平均配合间隙)为0.015 mm的情况下，通过改变阀芯倒锥半径差(锥台状阀芯的上下端面半径差)分别为0.010 mm、0.015 mm、0.020 mm和0.025 mm，笔者分别计算出了阀芯间隙流场云图，如图4所示。

图4 阀芯变锥度的间隙流场云图

从图4中可以看出：随着阀芯锥度的增加，偏心侧的压力下降显著加快，偏心侧与背离偏心侧的压力差逐渐增大，这将导致液压径向力逐渐增加，最终影响伺服阀的正常工作。

在给定的边界条件下，笔者通过对不同锥度阀芯间隙的流场进行仿真，得出了阀芯间隙的泄漏量，如表2所示。

表2 阀芯不同锥度的间隙泄漏量

由表2中可以看出：随着阀芯锥度的增加，伺服阀的泄漏量在明显增大；当阀芯倒锥半径差达到0.020 mm时，泄漏量为59.30 ml/min，大于额定最大泄漏量50 ml/min，这将会影响伺服阀的动态性能，延长系统的稳定时间。

因此，要尽量保证机液伺服阀芯的倒锥半径差不得大于0.015 mm，以确保机液伺服阀系统具有良好的稳定性。

3 系统控制性能仿真分析

前面笔者已通过对机液伺服阀芯配合间隙流场的分析，得出了不同阀芯锥度与偏心量下泄漏量的变化情况。

接下来笔者依据系统的阀控非对称液压缸数学模型，根据上述得出的泄漏量，在不同阀芯锥度下，利用仿真软件求解出了系统的阶跃响应曲线图，如图5所示。

图5 不同阀芯锥度系统阶跃响应图

在不同阀芯偏心量下，求解出了系统的阶跃响应曲线图，如图6所示。

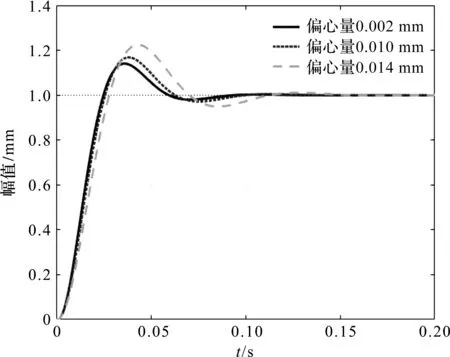
图6 不同阀芯偏心量系统阶跃响应图

由图(5，6)中系统的阶跃响应曲线可知：随着机液伺服阀芯锥度及偏心量的增大，系统的超调量在增大，调整时间也在增加，虽然系统依然处于稳定状态，但系统的稳定性能已逐渐变差；

为了保证系统具有较好的响应性能，要求本机液伺服控制系统的超调量不得超过20%。当机液伺服阀芯的倒锥半径差(锥台状阀芯的上下端面半径差)在0.015 mm，同时阀芯偏芯量在0.01 mm左右时，虽然系统的超调量相对较大，但未超过允许范围，而且系统的阻尼比有一定的提高，系统的稳定性有所提升，系统的动态性能满足要求；

但当阀芯的偏心量与锥度继续增大时，系统的动态性能会变差，超调量将大于20%，调整时间延长，其响应性能此时已无法满足系统的要求，导致机液伺服液压缸无法正常工作；

阀芯的偏心量与锥度的增加，导致了系统泄漏量升高，系统泄漏量增加虽然会增大系统的阻尼比，使系统的性能有所提高，但随着泄漏量的持续增加，一旦超过允许范围，系统的响应性能就会遭到破坏。

通过以上系统阶跃响应的分析，验证了笔者对于阀芯间隙流场仿真分析的正确性，并且系统阶跃响应图较为直观地表现出了系统动态性能的变化情况，这一结果可为风机用高速旋转机液伺服液压缸的结构优化分析奠定基础。

4 结束语

通过仿真分析，笔者研究了风机用机液伺服阀芯偏心量以及锥度变化对阀芯流场径向力和泄漏量的影响，并通过建立系统数学模型分析验证了仿真结果的正确性，得到了以下结论：

(1)随着高速旋转机液伺服阀阀芯偏心量的增加，阀芯的液压径向力逐渐变大，且指向偏心侧，泄漏量也明显增大；为了保证伺服阀的动态性能，在伺服阀装配过程中，要尽量保证阀芯与阀套的间隙不得超过0.010 mm；

(2)随着高速旋转机液伺服阀阀芯的锥度的增大，阀芯的液压径向力逐渐增加，泄漏量也显著增大；为确保系统具有良好的稳定性，要尽量保证机液伺服阀芯倒锥半径差不大于0.015 mm；

(3)在保证系统动态性能的同时，要尽量减小伺服阀芯锥度与偏心量，以降低系统稳态误差。

以上结论为集成式机液伺服液压缸结构的优化设计奠定了基础。