利用函数的不动点求数列的通项公式

钟 娇

（江西省南昌市立德朝阳中学 江西南昌 330026）

函数的不动点是被这个函数映射到其自身的一个点，即如果彐x0，使f（x0）=xo，则称xo为f（x）的一个不动点。

（1）代数意义：若方程f（x）=x有实根xo，则函数f（x）有不动点。

（2）几何意义：若函数y=f（x）的图像与y=x的图像有公共点（x0，y0），则xo为y=f（x）的不动点。

例1：已知数列{an}中，a1=1，an+1=2an+1，求数列的通项公式an。

解：因为an+1=2an+1，所以x=2x+1 x=-1，两边都减去不动点-1得an+1+1=2an+1+1，所以可以得到an+1+1=2（an+1）。

设an+1=bn，所以bn+1=2bn，数列{an}为等比数列，

故bn=b1·2n-1=2n，所以an=bn-1=2n-1。

则f（x）=kx+m

定理一：若f（x）=kx+m（k≠0，k≠1），p是函数f（x）的一个不动点，数列{an}满足：xn+1=f（xn），则xn+1-p=k（xnp）。

思考：递推函数具有什么结构，能够用取倒数？

是不是递推函数是分式函数都可以取倒数？

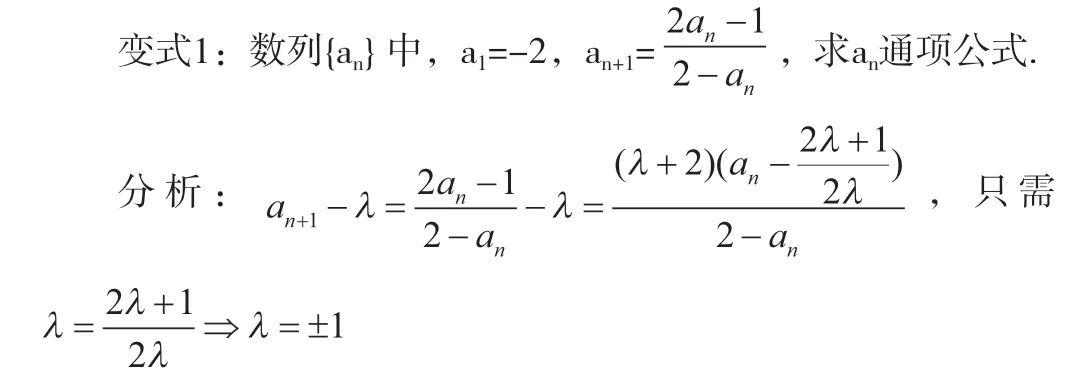
求出两个值，怎么办呢？

我们证明（1），同理可以证明（2）。

【小结】

本节本源探究微课程是从学生的难点入手，归纳几类可以选择利用函数的零点，求数列的通项公式的题型，实现了函数与数列的综合应用。并且对方法进行了整理，形成了定理。同时使学生的能力也得到了锻炼，如类比推理能力，划归与转化能力。