一只蚂蚁的思考

谢 川

（重庆市长征学校 重庆 400080）

近几年“最值问题”在中考中频繁出现，形式多样，主要综合了几何和函数两大部分的知识，难度较大。但通过探索研究会发现最值问题其实都可以转化为三大类的问题，一是二次函数配方求最值；二是转化为两点之间线段最短问题；三是垂线段最短问题。大家经常遇到的“胡不归模型”则可转化为垂线段最短，“阿氏圆模型”则可转化为两定点之间的路径问题。那么对于题目中说到的勾股定理里面的最值则主要是两点之间线段最短问题。

勾股定理具有独特的魅力，它是一个基本几何定理，勾股定理反映了直角三角形中三边之间的数量关系，从边的角度进一步刻画了直角三角形的特征，它可以解决许多直角三角形中的计算和证明问题，同时也在我们的实际生活中发挥着重要作用，是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一，所以它更是初中数学中一个重要的知识内容。

对于北师版教材来讲，《勾股定理》属于八年级上册第一章的内容，当我们学完勾股定理及其逆定理后，会进入到勾股定理的应用部分，课本上这一部分主要是探究蚂蚁在各种几何体上要吃到食物如何选择最短路径的问题，涉及的几何体主要有圆柱、正方体、长方体、台阶等常见的几何体，用到的解决方法通常是把几何体侧面展开，把立体图形问题转化为熟悉的平面图形问题，也就是运用“化曲为平”或“化折为直”的思想来解决问题。而现在要阐述的就是关于勾股定理应用这一节里我对于一个问题的思考。

在这堂课开始之前，我已经上过一次勾股定理的应用了，所以上课之前简单的备了一下课，胸有成竹的进入课堂，开启我自认为一切都会在掌握之中的课堂。

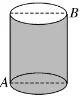
“同学们，请看到课本引例，A处的蚂蚁要想吃到B处的食物，它应该怎样走呢？”学生都能够想到各种各样的路径。“那请问怎样走才是最近的呢？”学生思考片刻，再加上我的实物演示及分析引导，基本上都掌握了找最短路径的方法，即是把圆柱侧面展开成一个长方形，在展开的平面图上确定蚂蚁和食物的位置，再利用两点之间线段最短画出路径，最后用勾股定理来解答。自认为讲解效果很好的我正准备进入下一个环节，一个学生打断了我：“老师，这种展开方式算出来的结果就一定是最短的吗？蚂蚁直接从A点垂直朝上走，然后沿圆柱的直径走到B就不能最短吗？”我愣了一下，不过我立马解释道：“那我们可以一起来计算一下这种路径的结果，比较一下这两种路径的结果。”最终在两个数据的有力说明下，这位同学若有所思的点点头，作为老师的我总算松了一口气，继续进行我的教学。

等到我下一次上课，我把所想的这个问题放在课堂上和同学们一起计算和探讨，这个结果让班上有疑惑的同学恍然大悟，也让同学们对这个模型认识得更全面，同时也让我对这个问题有了新的认识。但是要知道的是这个思考的结果只针对蚂蚁和食物的位置如引例所给的相对位置，一旦位置发生变化，那以上的结论显然不成立，至于在其它模型里面是否也有特殊的情况呢，大家可以再进行思考。

虽然这种有关勾股定理的最值在我们的中考试题中一般没有出现，但是对于学习知识来讲，我们不是为了应试而学习，多发现问题，思考问题，解决问题可以培养我们的思维能力。多思多问会让我们一身受益，所以任何一个出现的问题都值得我们去研究思考。

通过对这一问题的分析思考给了我两点启示：一方面，我明确的知道在课堂教学当中，作为教师要经常鼓励学生提出问题，思考问题，抓住每一次锻炼思维和培养兴趣的机会，体现学数学的本质。另一方面，作为一名教师，应该多进行教学反思，教学反思对教师自身教学水平的提高，以及对教学效果的提高都有举足轻重的作用。思考与反思是教师进步的阶梯，是教师进步的重要途径。