双频双星座地基增强系统精度和完好性算法
2020-09-22朱倚娴
胡 杰,周 玲,朱倚娴
(1. 运城学院物理与电子工程系,运城 044000;2. 南通大学机械工程学院,南通 226019)
0 引言
全球导航卫星系统(Global Navigation Sate-llite System, GNSS)以卫星作为导航信号源,构建了一个全球、全天候的高精度导航网络。GNSS在民用航空导航中的应用可以有效保障飞行安全和提高运行效率,但是飞机精密进近与着陆时对导航系统的精度、完好性、连续性以及可用性的要求较为苛刻,基于卫星信号本身的测距精度一般很难满足此要求[1-2]。地基增强系统(Ground Based Aug-mentation System, GBAS)通过建立位置已知的基准站,在采用差分技术提高测距精度的基础上,增加了一系列完好性监测过程,可有效增强其临近空域内GNSS性能,是未来唯一能够满足III类精密进近与着陆需求等级的GNSS增强系统[3]。基于全球定位系统(Global Position System, GPS) L1频点C/A信号增强的GBAS于2009年获得首次系统设计认证,并于2011年开展了I类地面系统设备与运行认证[4]。此后,在单频单星座(Single-Frequency Single-Constellation, SFSC)GBAS的基础上,相关学者提出了利用机载惯性导航系统辅助增强SFSC GBAS,以满足III类精密进近与着陆导航的需求[5-6]。目前,国内中电20所成功研制了我国首套GBAS,并在天津滨海国际机场完成了现场安装、飞行校验以及飞行认证等工作。其他研究机构,包括北京航空航天大学[7]、中电28所[8]等研究机构也在积极开展GBAS技术攻关,推动了该领域技术的进步。
GBAS通过完好性监测模块实时监测卫星信号状态,并将其中不满足完好性要求的卫星予以剔除。完好性监测过程虽然可以保证系统的完好性,但是由于可用卫星个数的减少导致卫星几何结构变差,即卫星几何精度因子变大,从而降低了系统精度和可用性。文献[9]中分析了可见卫星几何分布与GBAS机载保护级对应关系,根据分析可知,卫星几何分布结构对保护级计算影响较大,当可见卫星个数较少时,其对应几何分布相对较差,则计算得到的保护级可能会超出完好性告警门限,进一步导致虚警现象发生,降低了系统的可用性。为此,文献[10-11]中提出了利用Galileo与全球定位系统(Global Position System, GPS)进行组合,构建基于GPS/Galileo的双频双星座(Dual-frequency Dual-constellation, DFDC)GBAS,并分析了双星座以及双频对系统性能改善的影响。同时,由于载波相位观测噪声相比伪距观测噪声要小2个数量级,且受多路径误差影响更小,利用载波相位平滑可以有效提高伪距测量精度,因此,GBAS在计算伪距差分校正值前需要进行平滑处理[12]。Hatch滤波器是一种常用的平滑算法,其算法原理是利用一阶低通滤波器抑制码减载波(Code-Minus-Carrier, CMC)高频噪声。单频Hatch滤波算法中,若忽略历元间电离层梯度的影响,则滤波器平滑结果较为平稳;一旦电离层异常时,其平滑滤波结果会出现发散现象[13]。文献[14]将电离层风暴模型假设为分段线性模型,提出了一种非线性分歧排除算法,该算法计算量大,实现较为困难。文献[15]分析了电离层风暴对SFSC GBAS精度的影响,为消除电离层风暴梯度对滤波器平滑精度的影响,提出了通过实时监测电离层风暴时间梯度以自适应调节Hatch滤波器平滑窗口时间长度,该方法在一定程度上能够消除电离层风暴时间梯度对SFSC GBAS精度的影响。文献[16]中线性组合双频伪距和载波相位测量值,并将其作为Hatch滤波器的输入值,从根本上消除了电离层时间梯度和空间梯度对滤波器平滑精度的影响,但是其代价是引入一个增大的组合伪距测量噪声,从而降低了GBAS地面站系统精度。
本文在现有I类SFSC GBAS研究的基础上,将单星座扩展为包括北斗导航卫星系统(BeiDou Navigation Satellite System, BDS)在内的双星座,将单频升级为双频,开展DFDC GBAS精度和完好性算法研究工作。在提高系统精度方面,对双频无码载偏离(Divergence-free, Dfree)相位平滑伪距算法进行了研究,并利用采集得到的数据进行了算法性能验证;在系统机载完好性方面,给出了基于双星座的H0和H1假设下的机载保护级计算方法。利用实验室研制的DFDC GBAS原理样机进行了验证实验,实验结果验证了本文所提方法的有效性。
1 GBAS工作原理
GBAS是基于伪距测量的差分导航系统,能够消除地面站与机载端伪距观测值中时间与空间上的相关误差,包括卫星星历误差、卫星时钟误差以及电离层和对流层延时等。地面站子系统根据已知的基准站位置坐标以及接收机输出卫星星历和观测值,计算得到伪距差分校正值和完好性参数,并通过甚高频数据广播(Very-High Frequency Data Broadcast, VDB)电台向空域广播,机载用户接收卫星信号、地面站播发的伪距差分校正值和完好性参数,实现高精度定位与保护级计算。图1所示为GBAS信号流图。
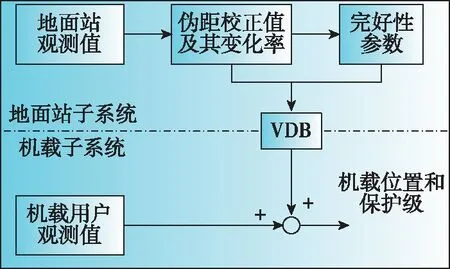
图1 GBAS信号流图Fig.1 GBAS signal flow diagram
基于GPS L1频点C/A信号的SFSC GBAS已获得国际民航组织I类精密进近与着陆许可认证,目前正在开展II/III类技术攻关研究。GBAS地面子系统在计算伪校正值前,需要对伪距进行平滑预处理,以抑制伪距测量噪声和多路径误差等。由于载波相位观测噪声比伪距观测噪声小2个数量级,且受多路径影响较小,因此利用载波相位对伪距进行平滑,可以有效提高伪距测量精度,且不存在整周模糊度固定问题。
1.1 Hatch滤波器及误差分析
GNSS伪距与载波相位测距可建模为[17]
(1)
式中,ρfi表示伪距测量值;r由卫星与接收机之间真实几何距离、接收机钟差和卫星钟差等效距离以及对流层延时等组成;ιfi表示电离层延时;ηρfi表示伪距观测噪声以及多路径误差等;φfi表示载波相位观测值;Nfi表示载波相位整周模糊度;ηφfi表示载波相位测距值噪声以及多路径误差等;其中,下标fi表示GNSS测距频点,实验室研制DFDC GBAS测距频点分别为GPS L1/L2和北斗导航系统(BeiDou Navigation Satellite System, BDS) B1I/B2I。
Hatch滤波器是一种广泛应用的载波相位平滑伪距方法,其算法框图如图2所示。
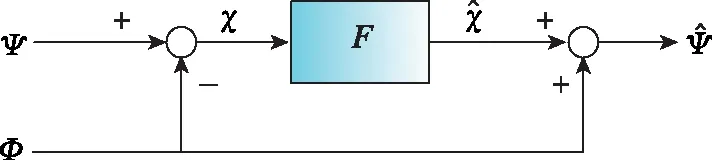
图2 Hatch滤波器算法框图Fig.2 Algorithm diagram of Hatch filter
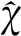
(2)
式中,τ表示滤波器平滑时间。对于SFSC GBAS而言,伪距和载波相位观测值分别为ρfi和φfi,因此,CMC可表示为
χ=ρfi-φfi
=2ιfi-Nfi+(ηρfi-ηφfi)
(3)
进一步经过低通滤波器后,可得平滑后CMC为
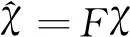
(4)
由式(1)和式(4)可得平滑后的伪距为
=r+Ifi+εfi
(5)
式中,Ifi表示经低通滤波后的伪距电离层延时,εfi表示经低通滤波后的伪距误差。
由式(5)可知,平滑后的伪距误差主要由伪距观测噪声和多路径效应组成。令平滑后的伪距误差εfi的标准差为σ,假设不同历元间的伪距观测噪声和多路径效应不相关,由低通滤波器传递函数可得σ的表达式可近似为
(6)
式中,σρfi表示伪距观测噪声以及多路径误差的标准差;Ts表示接收机相邻2个历元时间间隔,一般情况下τ取值远大于Ts。由式(6)可知,伪距经载波相位平滑后,其观测噪声和多路径效应误差得到抑制。
为分析电离层延时经Hatch滤波器后的误差变化特性,需建立电离层风暴数学模型。GBAS中常采用Stanford大学提出的电离层风暴模型进行误差分析[18]。如图3所示,该模型由4个典型参数表征,分别为:风暴梯度(30~400mm/km),宽度(15~200km),前锋速度(0~1000m/s),前锋前进方向和飞机接近方向的夹角(0°~360°),建立数学模型可表示为
ιfi(t)=I0+Idt
(7)
式中,I0表示电离层延时常值部分;Id表示电离层风暴梯度。
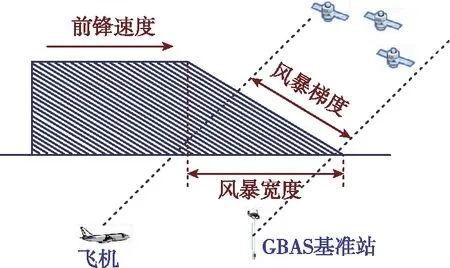
图3 Stanford大学电离层风暴模型Fig.3 Ionospheric storm model of Stanford University
进一步对式(7)进行Laplace变换可得,电离层风暴数学模型频域表达式为
(8)
令电离层延时经低通滤波后的变化量为ΔI,则根据式(5)可得ΔI的表达式为
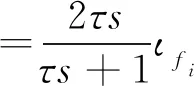
(9)
由式(8)和式(9)可知ΔI的稳态误差为
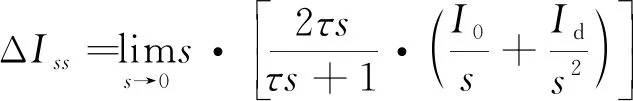
(10)
由式(10)可知,当电离层风暴梯度Id≠0时,经过低通滤波后电离层延时会产生一项额外常值偏置量,其大小与Hatch滤波器平滑时间τ成正。例如,当电离层风暴梯度为0.1m/min,滤波器平滑时间常数为100s时,低通滤波后电离层延时偏置量达到0.33m,这对GBAS而言是不可忽略的一项误差。
1.2 双频无码载偏离平滑算法
双频Dfree平滑算法通过线性组合不同频点的载波相位观测值,能够消除伪距平滑过程中电离层延时引起的额外常值偏置误差[18]。为此,本文拟将Dfree平滑算法的应用于DFDC GBAS中,下文将对Dfree平滑算法误差进行分析,首先式(11)和式(12)给出了电离层延时与载波频率之间的函数关系
(11)
(12)
式中,ιfi和ιfj分别表示卫星信号频点fi和fj测距所受到的电离层延时;Ne表示在卫星信号传播途径上横截面积为1m2的管状通道空间所包含的电离层总数量;根据fi和fj载波频率可以进一步求得α和β值。
由1.1节分析可知,电离层风暴时间梯度经过低通滤波后会产生一项额外常值偏置量。为了消除该常值偏置量,在卫星信号经过低通滤波器前,通过双频组合观测量消除电离层延时。为此Dfree平滑算法利用式(13)组合后的卫星信号观测量作为图2中低通滤波器的输入伪距和载波相位观测值
(13)
将式(1)和式(12)代入式(13)可得,低通滤波器输入载波相位观测值为
Φ=(r-ιfi+Nfi+ηφfi)-
(ηφfi-ηφfj)]=r+ιfi+NΦfi+ηΦfi
(14)
其中
(15)
与单频Hatch载波平滑算法相比,式(14)载波相位观测值中电离层延时符号发生的变化,与式(1)伪距观测值中的电离层延时符号变化具有一致性。因此可得载波相位组合后的CMC为
χ=Ψ-Φ
=(r+ιfi+ηρfi)-(r+ιfi+NΦfi+ηΦfi)
=ηρfi-(NΦfi+ηΦfi)
(16)
由式(16)可知,CMC中电离层延时被消除,因此,当CMC经过低通滤波器后,电离层风暴梯度不会产生常值偏置误差,平滑后的CMC可表示为
(17)
假设某一时间段内接收机锁定,载波相位无失锁或失周现象发生,因此,进一步可得经平滑滤波后fi频点的伪距观测值为
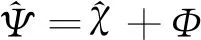
(18)
其中
εfi=Fηρfi+(1-F)ηΦfi
(19)
由式(18)可以看出,平滑后伪距电离层延时与式(1)原始伪距观测值中的电离层延时具有一致性,与式(5)相比,电离层延时没有产生额外常值偏置量。与单频平滑后的伪距类似,式(19)中残余平滑后的伪距误差εfi主要由伪距ρfi的测量噪声和多路径误差决定,因此,残余噪声和多路径误差的标准差与式(6)一样,可近似写成如式(20)所示
(20)
以1组BDS B1I和B2I双频观测数据为例,对Dfree平滑算法进行验证。图4所示为单频Hatch滤波平滑算法和双频Dfree平滑算法的CMC平滑精度对比曲线,低通滤波器的平滑时间常数取值为100s,由于CMC中包含载波相位整周模糊度,为了显示平滑滤波效果,图4中CMC初始值设置为0。
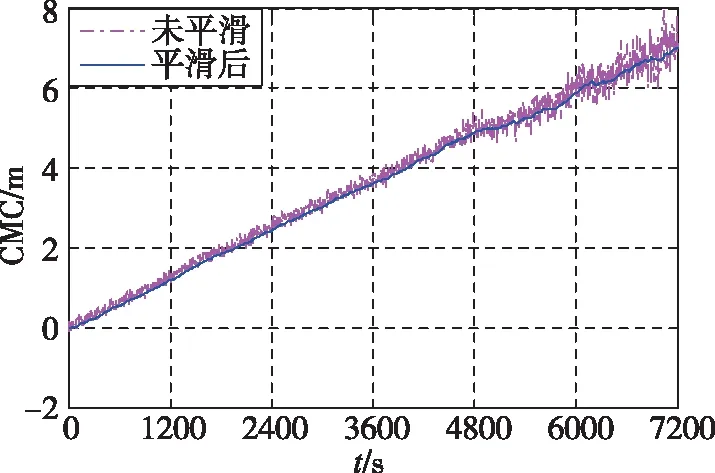
(a)单频Hatch滤波平滑算法CMC
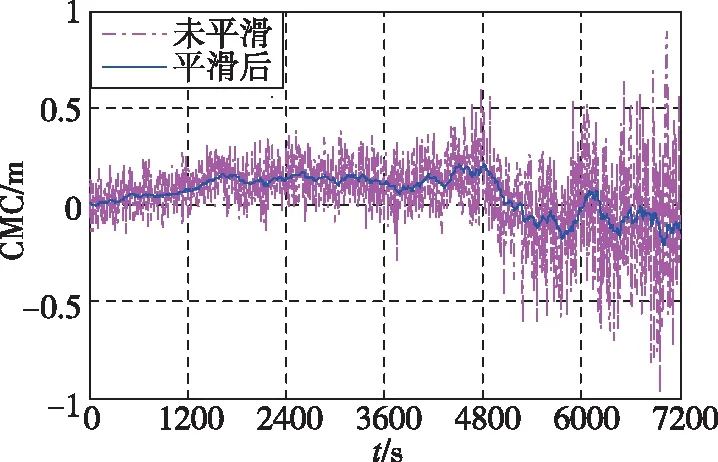
(b)双频Dfree平滑算法CMC图4 不同算法CMC平滑精度对比Fig.4 Comparison of CMC smoothing accuracy of different algorithms
由图4(a)可以看出,7200s观测时间内,电离层延时变化为3.5m(CMC中包含2倍电离层延时),CMC经低通滤波后其噪声得到明显抑制;由图4(b)可以看出,双频Dfree平滑算法中,以线性组合后的载波相位为低通滤波器输入时,CMC中电离层延时被抵消,因此,Dfree平滑算法能够有效隔离电离层风暴时间梯度对伪距平滑精度的影响。
1.3 载波相位周跳探测方法
Hatch滤波算法成立的前提是接收机锁定载波,但是由于卫星星座的变化、障碍物的遮挡、载体的运动等原因,滤波平滑过程中接收机周跳现象时有发生,如果不对周跳进行处理则滤波结果会发散。
当接收机处于锁定状态时,则载波相位整周模糊度N值保持不变,若对相邻2个历元的伪距和载波相位分别进行相减,则有
(21)
式中,Δρfi(k)和Δφfi(k)分别表示k时刻伪距和载波相位差分量;Δr(k)表示k时刻卫星与接收机之间的几何距离差分量;Διfi(k)表示k时刻电离层延时差分量;Δηρfi(k)和Δηφfi(k)分别表示k时刻伪距和载波相位测量噪声差分量;其中,k时刻伪距和载波相位差分量分别定义为
(22)
由式(21)可知,当电离层延时变化率无异常时,伪距与载波相位观测量之间有如下关系
λ·[φfi(k)-φfi(k-1)]≈ρfi(k)-ρfi(k-1)
(23)
根据式(23)可以得到周跳判别处理方法,令
temp=|λ·[φfi(k)-φfi(k-1)]-[ρfi(k)-
ρfi(k-1)]|
(24)
式(24)体现了相邻2个历元间的载波观测量的连续性,也称为载波差量,根据载波差量的大小可以判断载波是否发生周跳。
2 机载完好性算法
完好性是指当导航系统的定位误差超过运行所允许的误差极限时系统及时告警的能力,包括告警限(Alert Limit, AL)、告警时间和完好性风险3个指标。在实际飞行中,飞机的真实定位误差(Position Error, PE)虽然无法精确得知,但是可以建立理论上的置信界限,称为保护级(Protection Level, PL),PL为真实定位误差的置信概率为1-p的上限,即
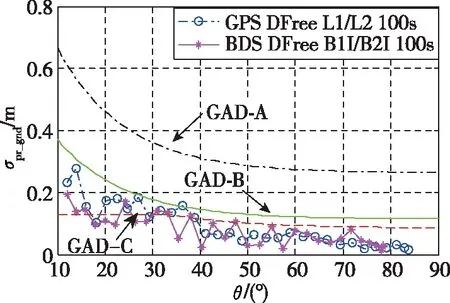
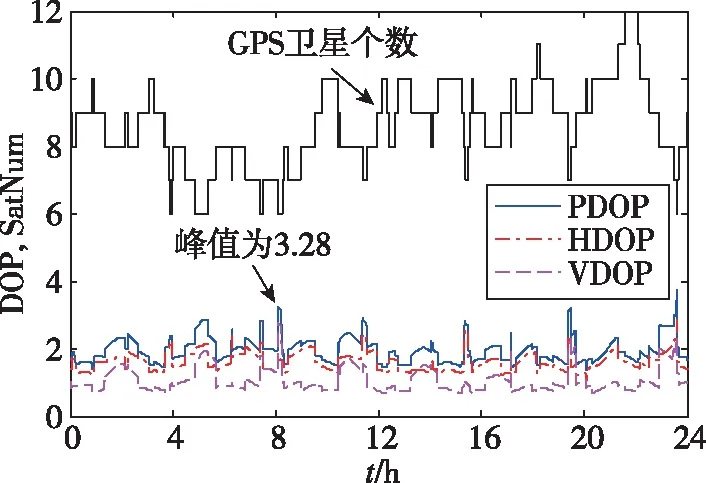
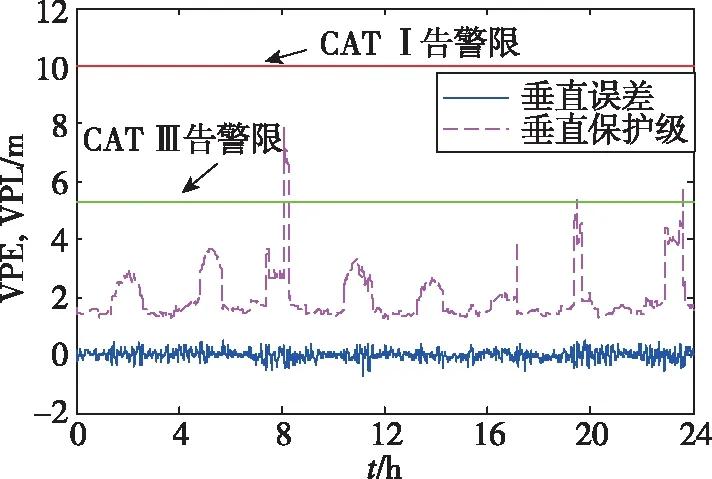
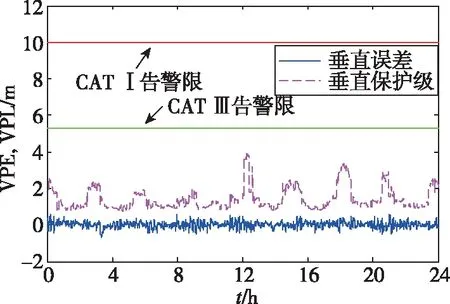
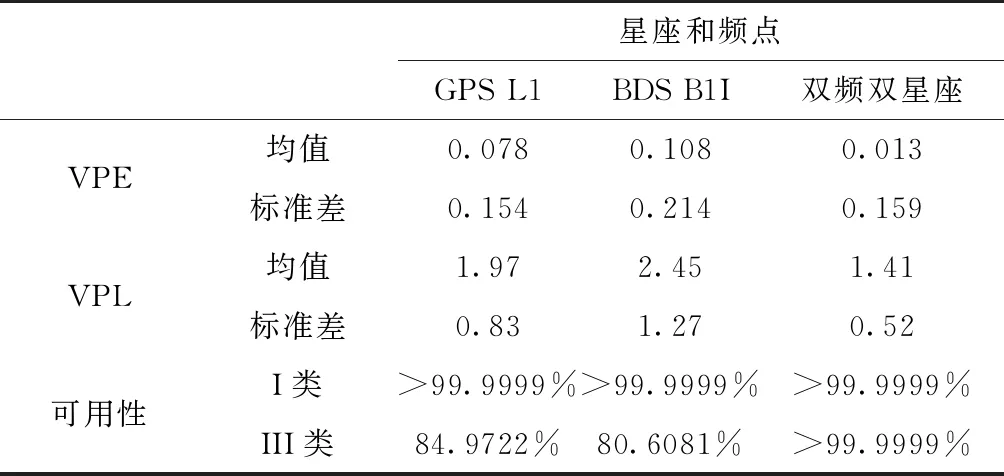
Prob(PE>PL) (25) 式中,p为所允许的完好性风险,与飞机进近着陆阶段的运行需求相关,约为10-7~10-9量级。因此,机载完好性监测的核心就是计算真实定位误差的高置信度上限,该计算过程也称为误差包络。PL包括侧向保护级(Lateral Protection Level, LPL)和垂直保护级(Vertical Protection Level, VPL)2个分量,其大小由卫星几何分布和差分校正后残余伪距测量误差标准差等决定,具有随时间变化的特性。 利用加权最小二乘法进行线性逼近可以得到机载用户位置和接收机钟差,线性化迭代方程为 Δy=GΔx+ε (26) 式中,Δy为N维向量,其中N表示可见卫星个数,由差分校正后的伪距测量值与基于卫星位置和用户位置(x)计算的距离作差求得;Δx为真实位置与计算得到的位置的差分量;ε为N维误差向量;G为机载用户接收机的几何矩阵,其表达式为 Gi=[-cos(θi)cos(αi),cos(θi)sin(αi), -sin(θi),1] (27) 式中,i表示第i颗卫星;Gi表示第i行向量;θi表示第i颗卫星仰角;αi表示第i颗卫星方位角。 进一步利用加权最小二乘法可得Δx最优解为 Δx=(GTWG)-1GTWΔy=SΔy (28) 式中,S=(GTWG)-1GTW表示加权最小二乘投影矩阵,用于将伪距域的信息投影到定位域;W表示伪距经差分校正后剩余误差项的协方差矩阵,其逆矩阵可表示为 (29) GBAS播发伪距差分校正值前,需要进行多基准一致性检验[19],通过计算单参考接收机故障导致的伪距差分校正值偏差的估计值(B值)来判别系统是否符合完好性需求。 (30) 式中,Bi,j表示第j个基准接收机上计算得到的第i颗卫星的B值;M表示地面系统可用接收机数量;PRci,k表示第k个基准接收机上计算得到的第i颗卫星的伪距差分校正值。由式(30)可知,Bi,j的大小表示基准接收机j对卫星i的差分校正值偏差的最优估计,符合高斯分布 (31) GBAS地面站计算所有可见卫星的B值,并根据B值计算σpr_gnd,然后将其广播给机载用户用于计算保护级。以1组实验数据为例,图5所示为地面站播发13号GPS卫星和11号BDS卫星σpr_gnd随卫星仰角变化曲线,其中,黑色点画线为标准RTCA DO-245A规定的GBAS地面精度指示器(Ground accuracy designator, GAD)A级曲线,绿色实线为GAD-B级曲线,红色虚线为GAD-C级曲线。 图5 σpr_gnd随卫星仰角变化曲线Fig.5 σpr_gnd changing curve with satellite elevation 由图5可以看出,σpr_gnd随卫星仰角变大而变小,分析原因可知,当卫星仰角较低时,电离层延时误差和多路径误差等引起的伪距测量噪声较大,因此进一步会导致计算得到的σpr_gnd偏大;同时,数据实验结果表明,实验室研制的GBAS原理样机的精度性能为GAD-A。 机载用户分别计算H0假设和H1假设下的LPL和VPL,并有 LPL=max{LPLH0,LPLH1} (32) VPL=max{VPLH0,VPLH1} (33) H0假设下的LPL和VPL计算如下 (34) (35) 式中,Kffmd为无故障漏检膨胀系数;slat,i和svert,i分别表示第i颗卫星侧距源误差在侧向和垂直方向上的投影;N表示机载用户所使用的测距源数量。 H1假设下的LPL和VPL计算如下 LPLH1=max{LPLH1,j} (36) VPLH1=max{VPLH1,j} (37) 式中,j表示GBAS地面系统的接收机编号,其取值为1,2,…,M。LPLH1,j和VPLH1,j的计算方法如下 LPLH1,j=|Bj,lat|+Kmdσlat,H1 (38) VPLH1,j=|Bj,vert|+Kmdσvert,H1 (39) 式中,Kmd表示地面子系统存在故障时的漏检系数;Bj,lat和Bj,vert分别表示基准站接收机引起的侧向和垂直方向误差;σlat,H1和σvert,H1分别表示侧向和垂直方向误差的标准差,其计算过程如下 (40) (41) (42) (43) (44) 实验室研制了GBAS原理样机,可实时接收BDS/GPS卫星信号,并对其完好性进行监测。地面系统包括:4个基准站及相应卫星接收天线、中心处理器以及VDB发射电台等;模拟机载系统包括:1个模拟机载接收机和卫星天线、机载数据处理单元以及VDB接收电台等。地面系统实时向周边空域播发可见卫星信号伪距差分校正值及其变化率、σpr_gnd、多基准一致性检验B值等,模拟机载系统根据接收到的卫星信号以及VBD报文进行差分定位并实时计算保护级,基准站和模拟机载系统GNSS天线实验室楼顶布局如图6所示。 图6 实验用GNSS天线位置Fig.6 GNSS antenna position for experiments 利用GBAS原理样机进行了24h长时间验证实验,以GPS为例,图7所示为卫星截止角10°时24h内GPS可见卫星个数(Satellite Number, SatNum)及其对应的精度因子(Dilution of Precision, DOP)曲线。由于飞机精密进近与着陆过程中,垂直方向的精度和完好性要求最为苛刻。因此以垂直方向为例,图8所示为机载用户(位置域)垂直定位误差(Vertical Position Error, VPE)和VPL随时间变化曲线。 图7 GPS可见卫星个数及其精度因子Fig.7 Visible satellites number and DOP of GPS 图8 SFSC GBAS垂直误差和保护级Fig.8 VPE and VPL of SFSC GBAS 由图7可以看出,当卫星截止角为10°时,24h内可见卫星个数最少为6颗,最多为12颗,卫星个数较少时,其相应的几何精度因子也相对较大。由图8可以看出,计算得VPL满足I类精密进近与着陆导航需求,系统24h内无非完好性事件发生。进一步对比图7和图8可以看出,当可见卫星个数为6颗且卫星几何分布较差时(即出现位置精度因子(Position Dilution of Precision, PDOP)峰值时),会导致VPL出现突变,最大值达到7.851m,使得该时间段不能满足飞机III类精密进近与着陆导航完好性告警限需求(VPL<5.3m),降低了系统的连续性和可用性。 由图9可以看出,GPS和BDS组合后可见卫星个数得到提升,24h内可见卫星个数最少为15颗,最多达到24颗,较好地优化了卫星几何分布,使其PDOP峰值由3.28减小为2.01。由图10可以看出,DFDC GBAS计算得到的VPL满足飞机III类精密进近与着陆导航需求,系统24h内无非完好性事件发生。进一步由表1可以看出,DFDC GBAS的III类可用性相比SFSC GBAS,由80.6081%提升到大于99.9999%,系统性能得到提升。 图9 GPS+BDS可见卫星个数及其精度因子Fig.9 Visible satellites number and DOP of GPS and BDS 图10 DFDC GBAS垂直误差和保护级Fig.10 VPE and VPL of DFDC GBAS 表1 SFSC GBAS和DFDC GBAS误差统计 本文针对SFSC GBAS无法满足飞机III类精密进近与着陆导航性能需求问题,提出了将我国的BDS与GPS进行融合,构建了一种新型的DFDC GBAS。对DFDC GBAS精度和完好性算法进行了研究,算法分析与实验结果表明: 1)双频Dfree载波相位平滑伪距算法通过线性组合不同频点载波相位观测值,能够有效隔离电离层风暴时间梯度对伪距平滑精度的影响,提高伪距平滑滤波精度。 2)BDS与GPS双星座融合后可见卫星个数得到提升,优化了卫星几何分布,进而使得系统的可用性由80.6081%提升为大于99.9999%,能够满足飞机III类精密进近与着陆导航性能需求。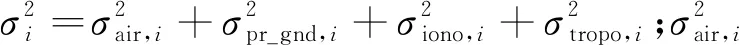
3 验证实验
3.1 实验环境
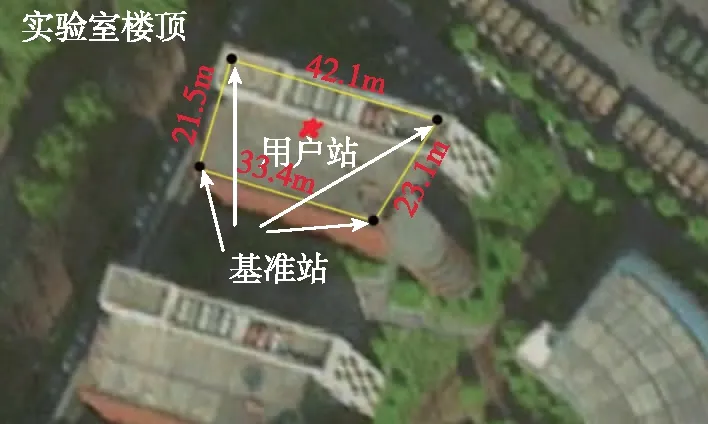
3.2 实验结果

4 结论
