卫星结构单轴与多轴正弦振动试验技术

马 蕾,王营营,冯 蕾,王松超,白 杨,文 祥

(1.上海卫星装备研究所,上海 200240;2.上海市特种设备监督检验技术研究院,上海 200062)

航天器在发射和飞行阶段要经受复杂严酷的动力学环境,因此,在研制过程中需要通过地面力学环境试验对航天器结构和载荷进行检验,通过将航天器(结构)暴露于特定振动环境中,发现航天产品在设计、制造、加工及装配等方面缺陷,验证产品在振动环境中的适应性和可靠性。

目前,国内航天器振动试验,通常采用单轴振动台3个方向依次进行单点激励振动试验,主要通过单轴电磁振动台,与垂直扩展台进行垂直向试验,与水平滑台进行水平向试验。单轴振动试验的条件是假设X、Y、Z3个方向的振动相互独立,即按照3个方向正交的振动响应进行包络来设计试验条件,以3个正交轴依次进行单轴振动试验覆盖真实发射过程中的多轴振动环境,试验和使用环境的差异通过加大试验量级和时间予以补偿。单轴振动试验方法比较简便易实现,但是随着航天器地面力学环境模拟技术的发展,产品性能复杂度不断提高,人们对航天器振动环境的研究也越深入,单轴振动环境考核方式暴露出一些严重的缺陷:单轴振动试验无法模拟多因素耦合的振动环境,难以真实复现实际振动环境中的故障模式,很多情况下,仅通过单轴振动试验考核的产品在实际振动环境中出现故障;单轴振动试验时,部分产品的侧向响应很大,在进行其他方向试验时造成“过试验”;多轴振动的多因素耦合效应不能简单地通过单轴振动叠加来定量估计,加大振动量级可能会产生与多轴振动试验不一致的故障模式;对大型试验产品的振动试验,单单进行单点单方向振动控制,振源和传递路径不一致,即使采用多点平均控制,也不能避免同一产品中的不同设备“欠试验”或“过试验”[1-3]。

航天器在实际发射和飞行阶段经历的振动环境本质是多轴同时发生的多轴振动,因此,要通过多轴振动试验对航天器进行试验考核,进一步发展多轴振动试验技术。

本文开展卫星结构单轴与多轴振动试验技术研究,应用多输入多输出控制方法,进行低量级单轴与多轴正弦振动对比试验,获得某卫星结构关键点的响应数据,并分析单轴与多轴振动不同正弦振动方式对结构响应的影响。

1 多轴振动控制算法

多轴振动试验控制系统的工作原理如图1所示。

利用振动台台面加速度传感器获取试件的动态响应信号,经过调理放大传输至控制系统,由控制系统对信号数据进行预处理后,再由系统控制算法迭代计算,输出相应的控制结果,因此,控制系统由3大部分组成:数据采集与传输、数据处理与存储和控制算法运算与输出。多轴振动试验控制系统的主要特点在于同时控制多个振动台产生相应的振动试验谱,区别于单轴振动试验控制系统主要体现在多振动台协调控制,控制算法复杂度高,在每一个频率点上的控制都以矩阵形式进行运算,计算量大,同时由于试件结构复杂,其控制以及监视通道要求很多,这些对控制系统的实现增加了难度。在对多点激励振动试验控制系统研究中存在着一些系统实现的难题,其中涉及的关键技术主要包括多通道数据实时传输与控制、相位控制技术、实时信号处理与控制以及振动试验控制系统体系[3-4]。

多轴多激励振动试验系统由振动台、试验件、工装夹具、功率放大器、传感器、控制器和数据采集器等组成的MIMO线性时不变系统。若系统为a个激励点和b个控制点的振动试验系统[4],如图2所示。

每一个驱动信号d(t)将对所有的控制信号c(t)产生影响,驱动信号与控制信号之间的关系可以表达为

(1)

将其进行傅里叶变换,转换到频域得

(2)

写成矩阵的形式为

(3)

即

{C(f)}=[H(f)]{D(f)}

(4)

式中:{D(f)}是驱动信号的谱向量,[H(f)]是控制信号与驱动信号之间的频率响应函数矩阵,{C(f)}是控制信号的谱向量。

多轴振动控制是在振动台上复现给定的输入试验条件即输入信号,通过对系统解偶,使输入激励信号{R(f)}与输出响应信号{C(f)}在误差范围内保持一致,根据式(4)得

{D(f)}=[H(f)]-1{R(f)}

(5)

利用式(5)对试验系统的频响函数进行求逆,得到系统的驱动信号。

1.1 多轴正弦振动控制算法

假设{R(f)}为多轴试验参考谱向量,它是参考频谱幅值和参考相位差的函数,[A(f)]为系统频响矩阵,[Z(f)]为解耦补偿矩阵,则{Em(f)}={R(f)}-{Cm(f)}为多轴振动控制系统第m次迭代的误差。其中,{Em(f)}为误差谱,{R(f)}为参考谱,{Cm(f)}为第n次迭代控制响应谱。则驱动谱矩阵为

{Dm+1(f)}={Dm(f)}+[G][Z(f)]{Em(f)}

(6)

式中:{Dm(f)}为第m次迭代驱动谱,{Dm+1(f)}为第m+1次迭代驱动谱,[Z(f)]=[A(f)]-1为解耦补偿矩阵,[G]为迭代增益矩阵。由于[A(f)]与[H(f)]存在误差,因此,驱动谱需要迭代修正[5-8]。控制算法见图3。

2 单轴与多轴正弦振动试验

为了进行多轴振动和单轴振动试验响应分析,以某卫星主体结构为试验对象,如图4所示,卫星共布设10个关键振动响应测点,测量振动加速度响应,其中2个位于结构的底板上分别为测点1和2,4个位于结构的上表面分别为测点4、8、3、5,4个测点位于侧翼上分别为6、7、9、10。其中控制加速度的布置位于振动台台面的中心位置。多轴振动试验系统如图5所示。

试验条件如下:频率范围为5～200 Hz,X、Y、Z3个方向,频率为5～10 Hz,振动量级为0.25g过渡到0.33g,频率为10～200 Hz,振动量级为0.33g。累计振动时间为不大于1 min。试验分别进行单轴正弦振动试验和三轴同振多轴振动试验。

给出本次单轴振动试验试验结果,每组分别进行X、Y、Z单轴向振动试验,幅值控制试验结果以及测点的加速度响应分别如图6～8所示。

三轴同振试验,选定Z轴为主振方向,X、Y向以Z轴作为相位参考,控制参数相位分别相差90°和180°,每组试验的试验量级分别按照前四组X、Y、Z单轴向振动试验的量级设定,如图9所示,为第三组试验条件下多轴正弦扫描振动10个测点加速度响应。

3 单轴与多轴振动等效性分析

通过试验数据,如表1和表2所示,对比分析了卫星模拟件在单轴振动条件下的响应以及三轴同振条件下的振动响应,在不同激振方式下,加速度响应峰值主要出现在悬臂结构部分,但对应的位置并不相同。其中,X向单轴激振条件下,其响应最大值位于10号点,对应Z向响应为114.1 Hz附近的14.08g;Y向单轴激振条件下,其响应最大值位于10号点,对应Z向响应为31.2 Hz附近的25.39g;Z向单轴激振条件下,其响应的最大值位于7号点,对应Z向响应为24.6 Hz附近的16.71g。三轴同振激振条件下,其响应最大值位于10号点,对应的Z向响应为152.6 Hz附近28.17g。以上峰值响应对比说明激振方式不同,结构动应力分布状态会存在差别[9-12]。

表1 单轴激振条件下的关键点加速度响应

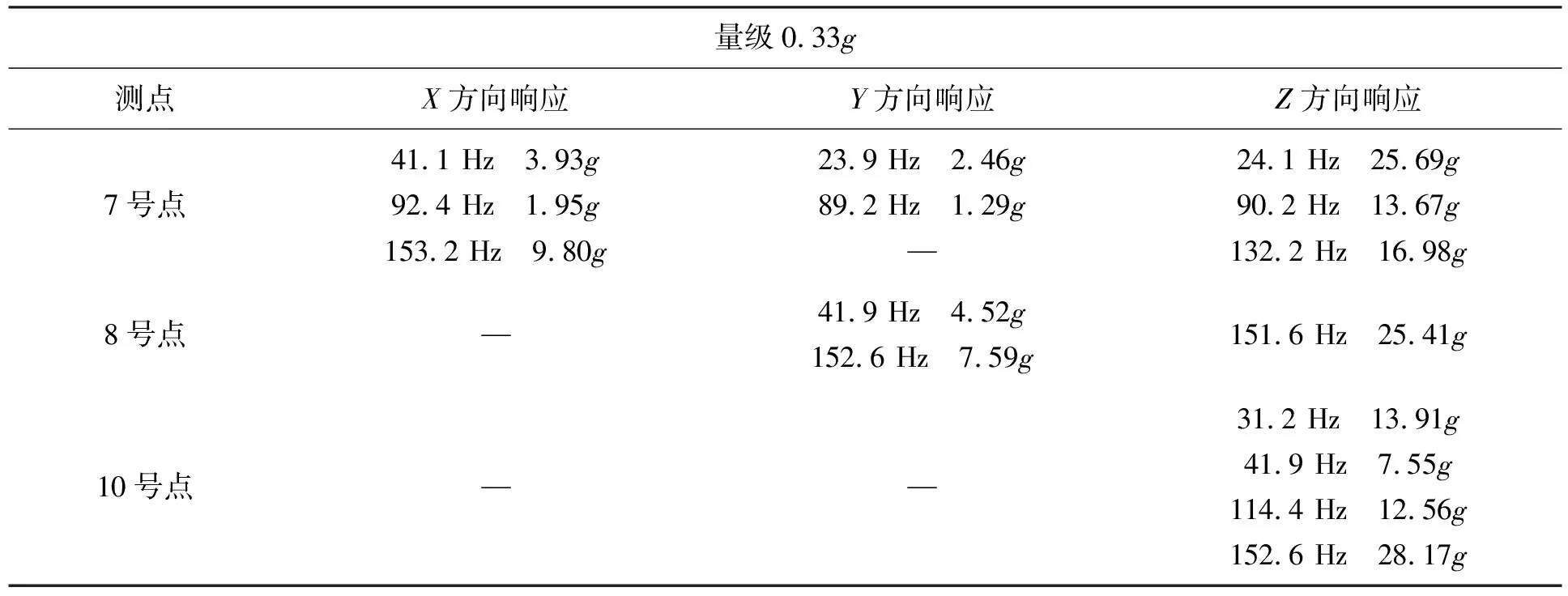
表2 三轴同振激振条件下的关键点加速度响应

(1)单轴振动只能激发当向振动加载方向的结构模态,多轴振动则能激发多个方向的结构模态,因此,多轴振动响应比单轴振动响应有更加丰富的共振峰[13-14]。如表1和表2所示,其响应的峰值大多出现在Z向,其余方向的峰值响应对应的模态较少。

(2)多轴振动条件下,结构在3个方向的共振频率均比单轴振动时偏低。量级为0.33g条件下,7号点Z方向的响应,X轴单向激振条件下,一阶共振频率为25.5 Hz,Y轴单向激振条件下,一阶共振频率单轴为24.6 Hz,Z轴单向激振条件下,一阶共振频率单轴为24.6 Hz,三轴同振激振条件下一阶共振频率24.1 Hz。

(3)通过对比不同量级下的单轴和多轴关键点的加速度响应,三轴同时加载比单轴单独加载所产生的等效应力响应最大值更大,以测点7为例,当量级为0.33g的条件下,X、Y、Z3个方向的单轴振动最大响应分别为114.19 Hz附近的14.09g,134.3 Hz附近的18.46g,24.68 Hz附近的18.71g;三轴同振情况下,其响应达到24.09 Hz附近的25.69g,测点10在152.61 Hz附近最大达到28.17g。综上可知,三轴同时加载比单轴加载时测点处加速度响应更大,尤其在结构的固有频率附近。对经受多轴振动试验的产品,若按单轴振动依次加载进行3个方向单轴近似试验,会使响应与真实结果存在一定偏差,存在不同程度“欠试验”或“过试验”风险。

(4)进行响应近似等效剪裁分析,以结构关键点单轴振动加速度控制响应谱为基准,求解与之等效的三轴振动各方向控制谱的谱值缩小系数。令3个轴向控制谱裁减系数分别为t1、t2、t3。设置初始值t1=t2=t3=0.1,反求载荷谱,提取关键点处3个轴向的小量级正弦激励响应,根据振动激励与响应的关系,利用计算关键点处3个轴向的加速度响应值建立循环。计算变量t1、t2、t3在0.1～1范围内变动时,通过关键点处3个轴向的加速度响应值的所有情况,确定剪裁系数。以3个单轴向正弦振动量级为0.33g,测点7响应为例,优化计算3个轴向控制谱的裁减系数分别为0.645 2、0.687 1、0.314 2,其裁剪过程如图10所示。其余测点响应类推。

4 结论

本文通过某卫星壳体结构为试验对象,分别进行单轴和多轴的对比试验,通过开展对卫星产品的多轴与单轴振动等效性研究,对多轴振动试验的等效性进行试验验证。研究结果表明,多轴振动可以激发产品在不同方向的结构模态,且响应具有更丰富的共振峰;多轴振动条件下,结构在3个方向的共振频率均比单轴振动时偏低;三轴同时加载比单轴单独加载所产生的等效应力响应最大值更大。考虑到多轴振动和单轴振动相比存在的差距,多轴振动引起的结构响应更加复杂,从统计能量的角度讲,单轴和多轴的等效需要大量现场的测试数据作为等效的基础,后续将对不同结构类型卫星进行多轴振动试验,积累更多单多轴振动试验数据,进一步对多轴振动试验条件进行剪裁与优化。