Optimizing the capacity of standalone hybrid renewable energy power generation system by improved artificial bee colony algorithm
2020-09-20YangYongLiRongGuoSuLiuDeyou
Yang Yong, Li Rong, Guo Su, Liu Deyou
Optimizing the capacity of standalone hybrid renewable energy power generation system by improved artificial bee colony algorithm
Yang Yong1,2, Li Rong1,2※, Guo Su2, Liu Deyou2
(1.,,211167,; 2.,210098,)
To obtain the optimal capacity and analyze the relationship between the optimal Levelized Cost of energy and the loss of power supply probability of a wind/photovoltaic/battery hybrid power generation system, a capacity optimization method based on an improved artificial bee colony algorithm was proposed. Firstly, the component models of the hybrid power generation system (wind turbine, photovoltaic, battery, and grid loads) were established and the rule-based energy management strategy was carefully designed to coordinate the different components of the hybrid power generation system. According to whether the electric power generated and converter capacity was sufficient, the energy management strategy was designed as four scenarios and the corresponding rules were designed; Secondly, the model for the capacity optimization problem was built with the objective function of minimizing the Levelized Cost of energy, where the requirement of satisfying the loss of power supply probability was handled as a constraint; Lastly, the penalty function method was applied to handle the loss of power supply probability constraint and an improved artificial bee colony was applied to improve the accuracy of the solution to the capacity optimization problem. In the algorithm, differential evolution operators were introduced to balance the bees’ ability of exploration and exploitation in different stages of the optimization process and a new food source could be generated by differential evolution operators with a probability increasing adaptively with the iterations in the employed bee stage. To verify the effectiveness of the algorithm, contrast tests with artificial bee colony and differential evolution were performed. The comparison results showed the proposed algorithm had better accuracy, robustness, and convergence rate. Then, to obtain the relationship between the optimal Levelized Cost of energy and the loss of power supply probability, capacity optimizations of the hybrid system was performed under the different loss of power supply probability requirements, which was changed from 0 to 5% with an equal step of 0.1%. Results showed that the Levelized Cost of energy decreases with the increase of loss of power supply probability and the descent rate was gradually decreased. This implied that it could obtain more obvious economic benefits by reducing the reliability requirement appropriately when the loss of power supply probability was at a smaller value. Furthermore, the influence of main parameters, such as the initial capital of the main component (wind turbine, photovoltaic, and battery) and meteorological resources (annual average of solar radiation and wind speed) on the Levelized Cost of energy was carried out by sensitivity analyses. The sensitivity analyses of the initial capital of the components were carried out by capacity optimizations of the hybrid system with different initial capital values of (wind turbine, photovoltaic, and battery system), which were changed from 60% to 140% of their best estimate value, the results showed that the influence of initial capital on the Levelized Cost of energy presented a linear relationship, the line of the photovoltaic was with the highest slope, and the line of the battery had the lowest slope. This implied that it could generate more obvious economic benefits by reducing the photovoltaics’ initial capital. The sensitivity analyses of the meteorological resources were carried out by capacity optimizations of the hybrid system with different annual average values of solar radiation and wind speed, which were changed from 80% to 120% of their best estimate value, the results showed that the influence of meteorological resources on the Levelized Cost of energy presented a linear relationship, and the slope of wind speed was higher than that of the solar radiation. This implied that it should pay more attention to the wind resource evaluation.
renewable energy resources; optimization; algorithms; hybrid power generation system; artificial bee colony algorithm; differential evolution operators; optimal sizing; sensitivity analysis
0 Introduction
Nowadays, the interests of using renewable energy were increased as the conventional fuel reserves were finite and depleting rapidly. Due to the complementary characteristics of wind resources and solar resources, the Hybrid Renewable Energy System (HRES) consisted of Photovoltaic (PV) and Wind Turbine (WT) became a popular choice to meet the electricity demand in remote and island areas[1]. The integration of energy storage systems, such as Battery System (BS), or conventional energy resources, such as Diesel Generators (DG) improved the reliability of the HRESs[2]. For HRESs, capacity optimizing was a key factor to attain a reliable supply at a low cost[3], but it was a complicated task because the optimal configuration depended on the knowledge of energy sources, technical specifications, environmental conditions, and load profiles[4].
The optimal sizing methodologies reported so far could be categorized into three classes: classical algorithms, software tools, and modern techniques[5]. Classical algorithms were based on mathematical derivation, theoretical analysis, and calculations. Nogueira et al.[6]presented a sizing methodology based on simulation tools and linear programming for an autonomous PV-WT hybrid system achieving minimum cost and high reliability, and statistical models based on Beta and Weibull were applied for the solar and wind power. A Mixed-Integer Linear Programming (MILP) model for an isolated PV-WT-BS-DG hybrid system was presented[7]. The optimal sizing problem with load response considered was established in the MILP framework and solved by combining of Hybrid Optimization Model for Electric Renewables (HOMER) and the General Algebraic Modeling System (GAMS)[8]. A double-layer decision model for the storage capacity configuration of PV-WT-BS HRES was established and solved by dynamic programming[9].
Many researchers used software tools to design and optimize HRES. HOMER[10]developed by National Renewable Energy Laboratory (NREL) was one of the most popular softwares. It was capable of simulating and optimizing energy systems including renewable and conventional sources, and energy storage systems for both standalone and grid-connected modes[11-12]. HOMER was used for techno-economic optimization and analysis of a PV-BS HRES[13]. System performance of a PV-DG-BS HRES based on technical, economic, and environmental constraints, was analyzed by HOMER[14]. Rajbongshi et al.[15]focused on the design of a PV-BS-DS HRES and the system configuration was optimized under different load profiles. The optimum performance of a fuel cell and PV HRES for standalone applications were calculated by HOMER, where components capital and replacement cost used by HOMER was computed by the fuzzy logic program[16]. However, the software had the limitations that it performed only a single-object optimization and the input variables should be inserted by the user[11].
Modern methods, applying swarm intelligence to optimize the component size of the HRES, were more flexible in dealing with complex optimization problems and could achieve more accurate results[5]. A hybrid algorithm integrated Genetic Algorithm (GA) with Particle Swarm Optimization (PSO) and a multi-objective PSO algorithm was applied for the optimal sizing of a WT-PB-BS HRES[17]. Singh et al.[18]applied an Artificial Bee Colony (ABC) algorithm to detect out the optimum hybrid system configuration for a PV-biomass HRES with the least Levelized Cost of Energy (LCOE) and proved that the ABC algorithm provided better results as compared with HOMER. The harmony search algorithm was applied to the optimal configuration for a PV-WT-fuel cell-biomass HRES and sensitivity analysis of the initial capital cost of the fuel cell was also studied[19]. Sharma et al. applied grey wolf optimization for optimal sizing of PV-WT-BS HERS and pointed out that grey wolf optimization outperformed several existing optimization techniques such as GA, PSO, and tabu search algorithm[20]. A multi-objective self-adaptive Differential Evolution (DE) algorithm was applied for the optimal sizing of a PV-WT-DS-BS HRES in Yanbu, Saudi Arabia[21]. Minimizing the life cycle cost, CO2emissions, and dump energy were considered simultaneously for the optimal sizing of PV-WT-DS-BS HRES and was solved by GA[22]. The non-dominated sorting genetic algorithm was used in the design of a standalone PV-WT-BS HRES with objective functions of total cost minimization and reliability index maximization, and uncertainties of renewable resources were addressed by chance-constrained programming[23].
With the rapid development of HRES, intelligent optimization algorithms with better performance were urgently needed. ABC was a relatively new stochastic swarm intelligence optimization inspired by the foraging behavior of honey bee and had shown promising performance on various complex optimization problems[24-27]. However, ABC performed well in exploration but relatively poorly in exploitation, which led to a slow convergence[28]. A possible explanation might be that ABC exploited its solution search equation to generate the new solution by changing one variable at a time[29]. Unlike ABC, DE generated the new solution by differential operators, i.e., mutation and crossover, which ensured that at least one variable was changed at a time. Accordingly, DE tended to exploit well and showed a fast convergence rate[30-31]. From this perspective, the performance of the optimization algorithm might be improved by hybridizing ABC with DE.
In this study, a hybrid ABC algorithm with DE (namely ABCDE) was applied to the capacity optimization of WT-PV-BS HRES located in a remote area in Xining, China. In the algorithm, the candidate solution could be generated by mutation and crossover according to an adaptive increased probability during the employed bee stage and its effectiveness was verified by contrast tests with ABC and DE. Then, the techno-economic analysis of the HRES was presented and the relationship between reliability and economy of the hybrid energy system was obtained by solving the optimization problem under the different Loss of Power Supply Probability (LPSP) requirements. Furthermore, sensitivity analyses were performed to research the influence of the initial capital of the main component (PV, WT, and BS) and meteorological resources (annual mean value of solar radiation and wind speed) on the LCOE.
1 Mathematical model and energy management strategy
The structure diagram of the HRES was shown in Fig.1. It consisted of five major components: PV systems, WT systems, a converter, BS, and grid loads.

Fig.1 Structure diagram of the Hybrid Renewable Energy System (HRES)
1.1 Component model
1.1.1 Wind turbine
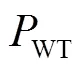

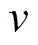

1.1.2 PV panel


1.1.3 Battery bank
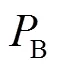
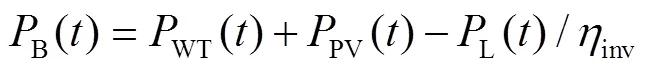

where Δrepresented the interval of adjacent periods, h.
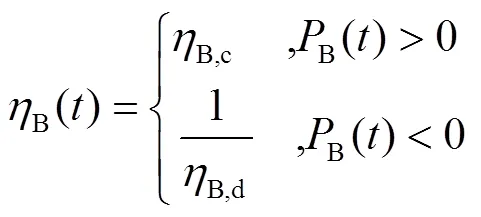
Moreover, the battery’s state of charge should satisfy the constraint described as Eq.(7)

1.1.4 Loads

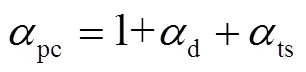
1.2 Energy management strategy
To meet grid load requirements as much as possible, a rule-based Energy Management Strategy (EMS) coordinating components’ output power of the HRES was designed. In this study, the Loss of Power Supply (LPS, kW) caused by the shortage of electric power generated and converter capacity were both considered.
pwas defined to indicate whether the electric power generated was sufficient and was calculated by Eq. (9). Ifpwas large than 0, it meant electric power generated was sufficient.
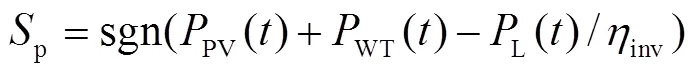
cwas defined to indicate whether the converter capacity was sufficient and was calculated by Eq. (10). Ifcwas larger than 0, it meant converter capacity was sufficient.
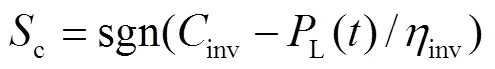
According to the combination values ofpandc, the rule-based EMS was designed as 4 cases.
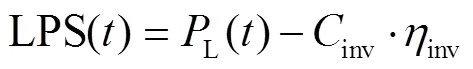
and the extra energy calculated by Eq. (12) would charge the batteries as case 1.


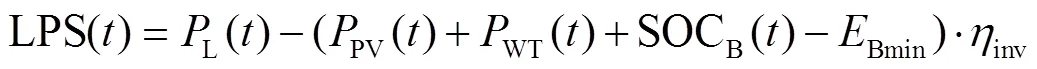
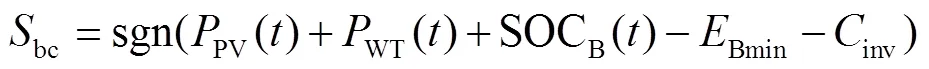
1.3 Objective function and constrains
The objective function of the optimal problem shown as Eq. (16) was minimizing LCOE (lcoe, $/kWh) while satisfying the reliability requirement represented by LPSP (lpsp, %).
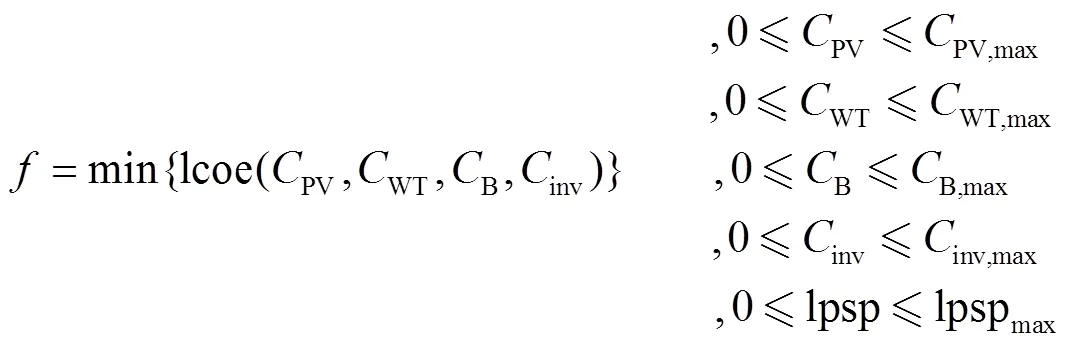
LCOE of the HRES could be calculated by Eq. (17)
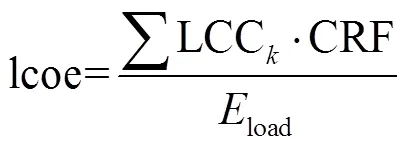
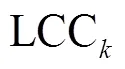
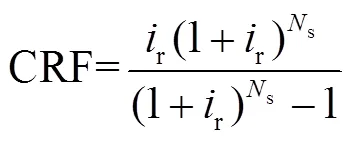

wherendenoted the nominal discount rate, %; idenoted the expected inflation rate, %.

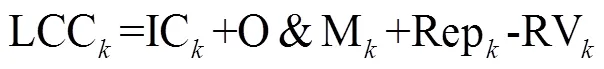

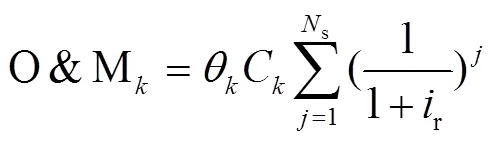
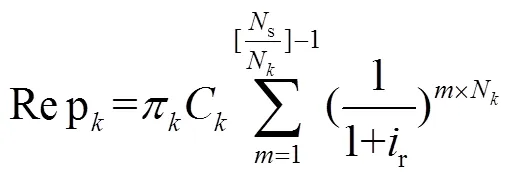
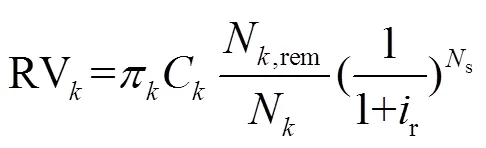


LPSP of the HRES was calculated by Eq. (27)
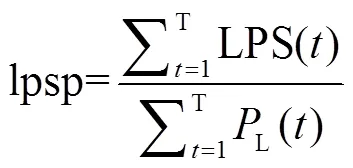
where T=8 760 h was the total number of cycles.
2 The algorithm ABCDE
2.1 The conventional ABC
In ABC, the solutions to the problem were represented by food resources. The process of seeking the optimal solution was similar to that of seeking the best food resources by bees. The bees in the algorithm were divided into three categories, that was employed bees, onlooker bees, and scout bees. ABC included 4 basic stages namely the initialization stage, employed bee stage, onlooker stage, and scout bee stage.
1) Initialization stage and fitness function
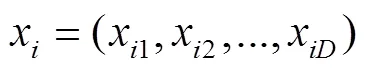
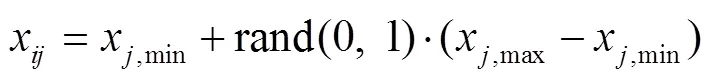
After initialization, the fitness of the food resource could be calculated by Eq.(29)
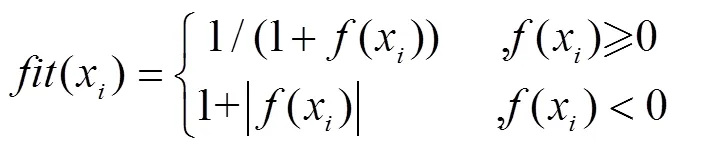
2) Employed bee stage
In this stage, each food resource was exploited by one employed bee, and a new candidate food resource could be generated by Eq.(30)
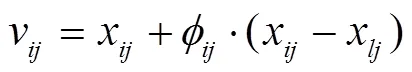
wherewas randomly chosen from {1,2,…,};() was randomly picked up from{1,2,…,SN};was a random number in the range of [-1,1]. Noted that according to Eq.(30), only the-th dimension of the new resource was different from the original one. If the fitness of the new resource was better than that of the original one, replacedby, otherwise,was kept to the next generation.
3) Onlooker bee stage
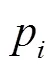
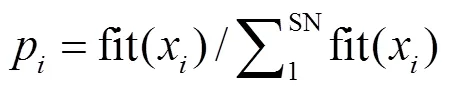
4) Scout bee stage
If the fitness of a food resource kept unimproved over a predefined time, the associated employed bee abandoned its current food resource and became a scout bee to search a new food resource generated according to Eq. (28). Noted that there was a maximal one scout bee in each generation.
2.2 The ABCDE
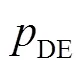
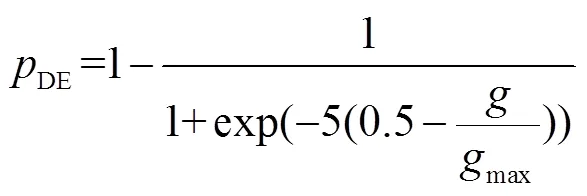
Differential operations included mutation operators and crossover operators. Many variant mutation operators had been developed, and DE/rand/1 shown as Eq. (33) was chosen


With regard to crossover operator, there were two frequently-used schemes namely binomial crossover and exponential crossover, and binomial crossover expressed as Eq.(34) was chosen.
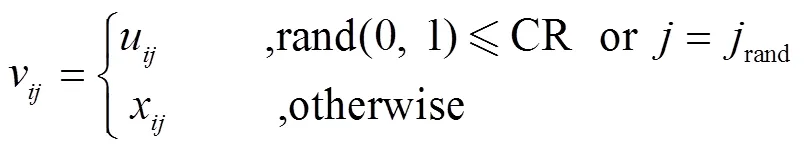
The steps of ABCDE could be summarized as follows:

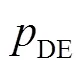
Step 3, onlooker bee stage. Assigned onlooker bees for food sources according to their probability calculated by Eq. (31), exploited the food resource by Eq. (30), and updated food source similar to employed bee stage. When all of the onlooker bees had exploited the food resources, set=2×.

3 Case study
3.1 Data

3.2 Algorithm contrast
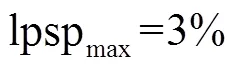
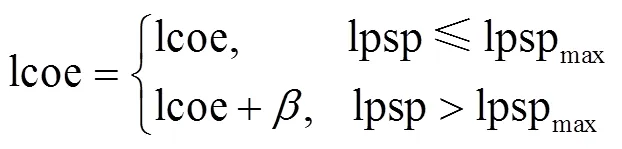
where was a number with a large value.
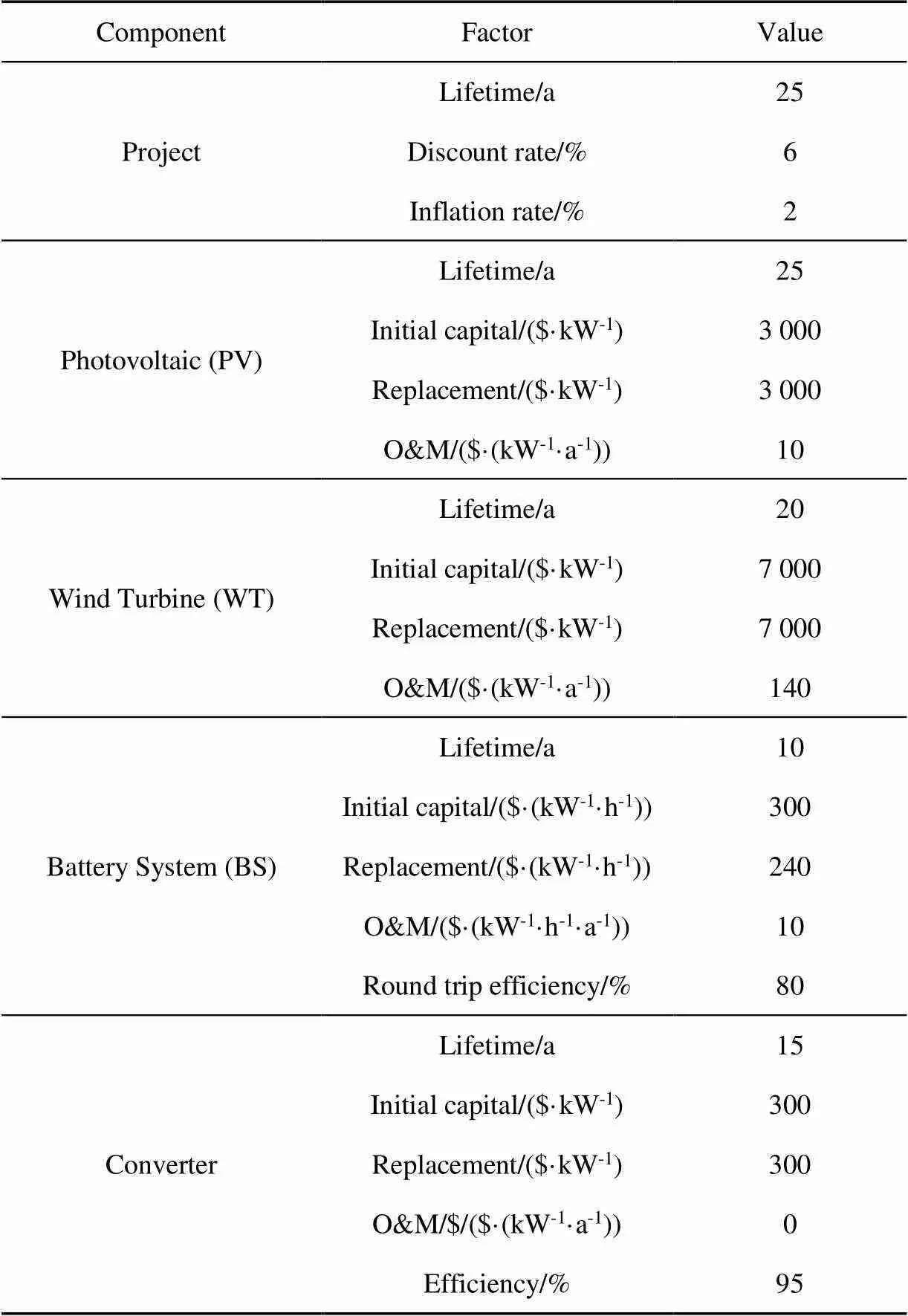
Table 1 Economic and technical parameters of the component
In an intelligent optimization algorithm, each individual represented a set capacity of components. For any individual, a one-year continuous simulation of HRES could be performed according to the EMS (section 2.2). After the simulation, the LPSP and LCOE could be calculated, and then the individual’s fitness value was obtained. The evaluation process for each individual of ABC, DE, ABCDE was shown in Fig.3. The optimization results were presented in Table 2, and the convergence curves of the mean values obtained by the three algorithms in 10 runs were shown in Fig.4.
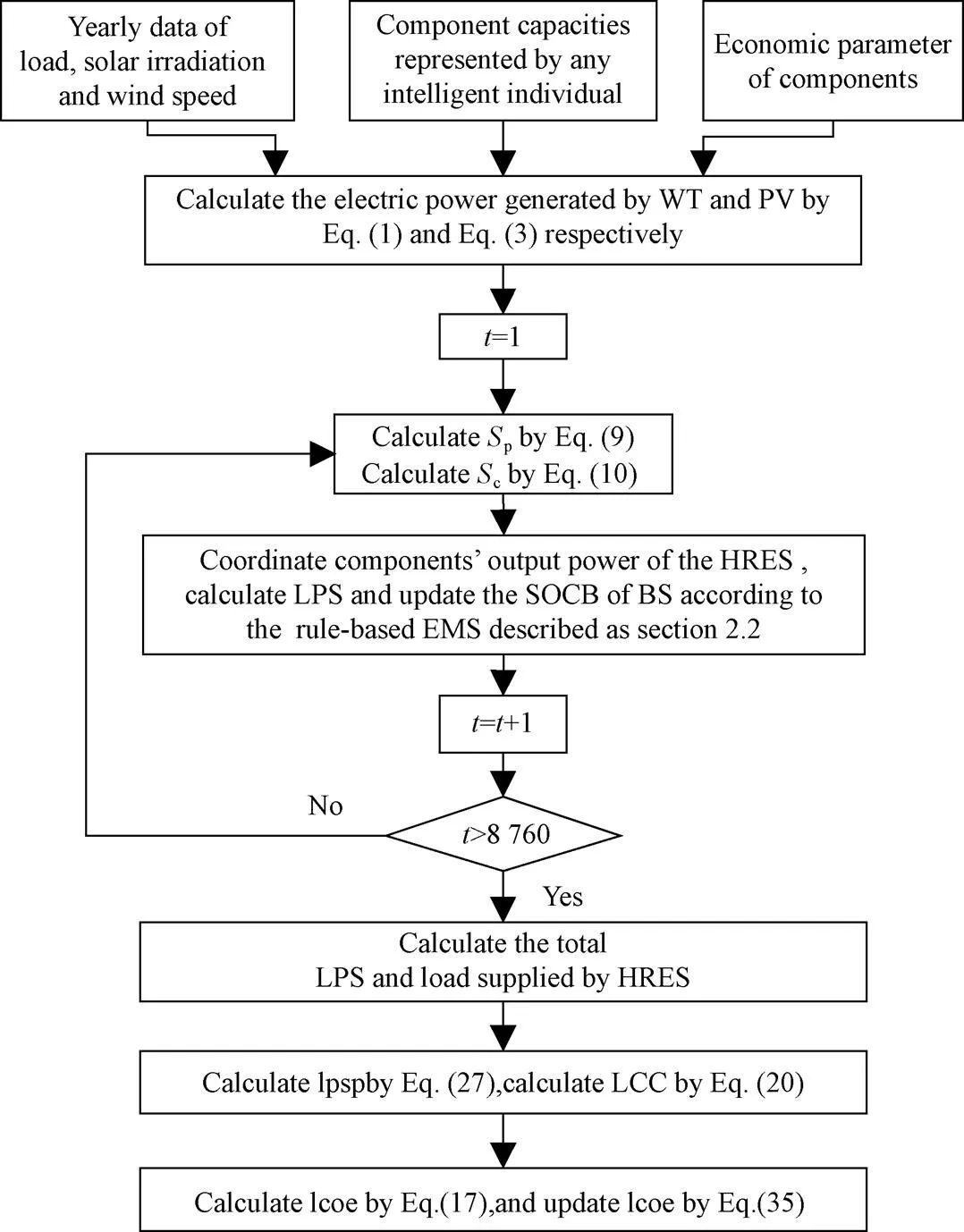
Note: WT meant wind turbine; PV meant photovoltaic; BS meant battery system; HRES meant hybrid renewable energy system; EMS meant energy management strategy. t denoted the time index; Sp denoted whether the electric power generated was sufficient; Sc denoted whether the converter capacity was sufficient; LPS denoted the loss of power supply, kW; SOCB denoted the state of charge of the battery, kWh; lpsp denoted the loss of power supply probability, %; LCC denoted the life cycle cost, $; lcoe denoted the levelized cost of energy, $·kWh-1.
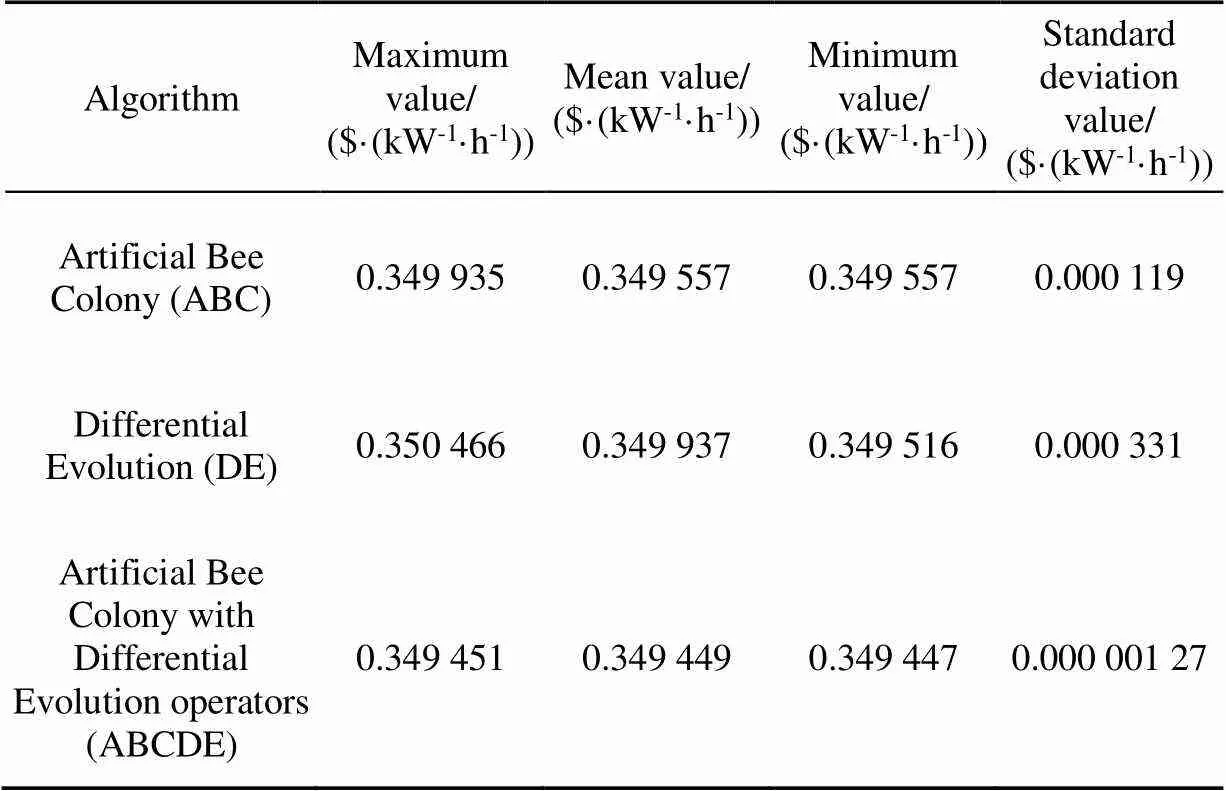
Table 2 Optimization results of algorithms
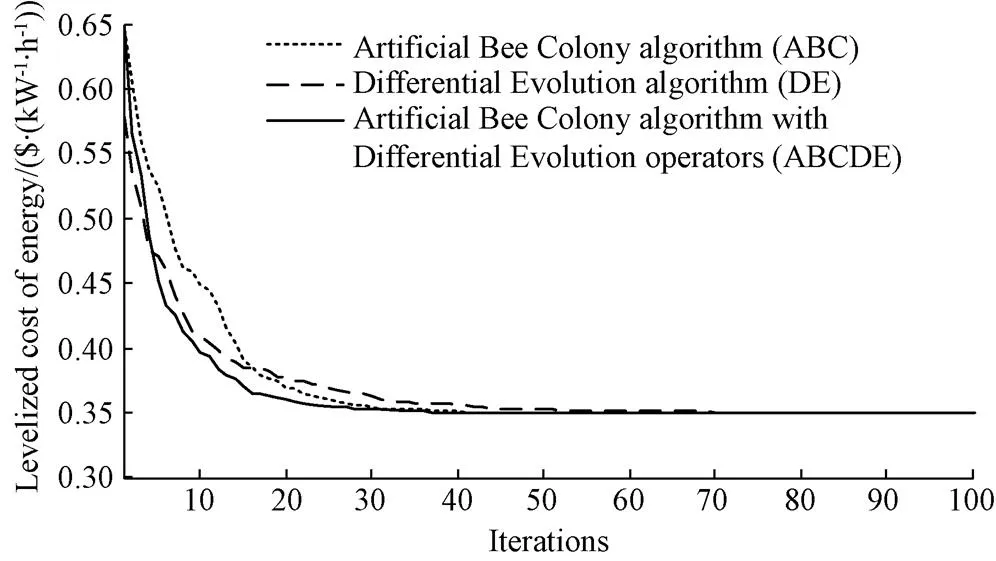
Fig.4 Convergence curves for the mean values of the levelized cost of energy with different algorithms
From Table 2 and Fig.4, it could be concluded that ABCDE had better accuracy, robustness, and convergence rate compared with the other reference algorithms.
3.3 Economic-technical analysis

Fig.5. Capital distribution for each component of the Hybrid Renewable Energy System (HRES)

From Fig.6, it can be seen that economy and reliability were contradictory indicators, if the high reliability was required, the investment cost would increase, and the decline rate of LCOE decreased gradually with the growth of LPSP.

Fig.6 Relationship of Loss of Power Supply Probability (LPSP) and Levelized Cost of Energy (LCOE)
3.4 Sensitivity analysis
1) Sensitivity analysis for component initial investments
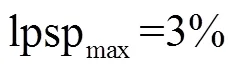
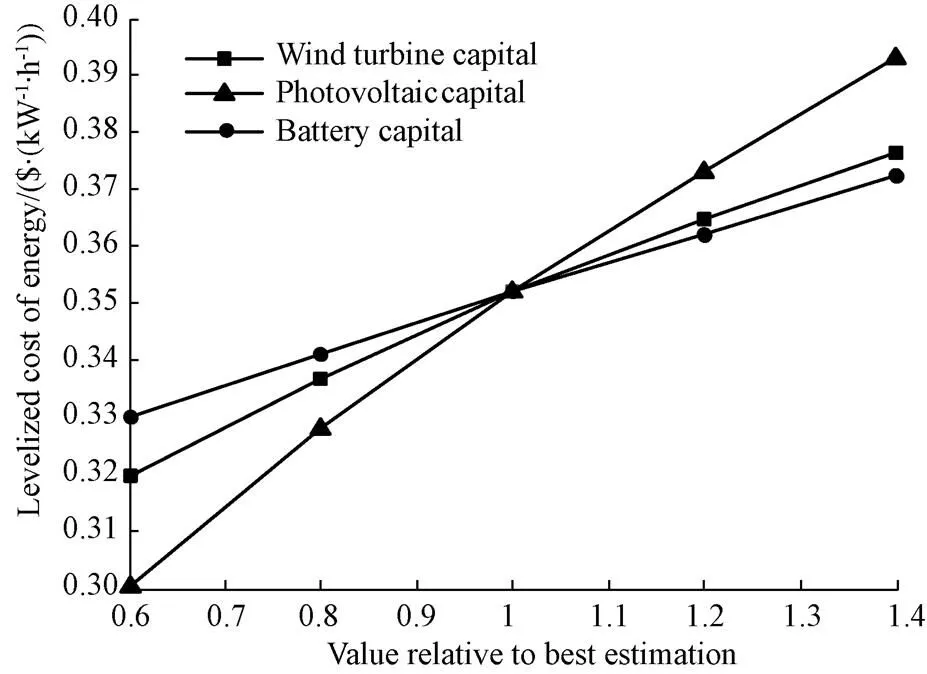
Fig.7 Effect of components’ initial capital on the Levelized Cost of Energy (LCOE)
2) Sensitivity analysis for meteorological resources
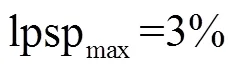
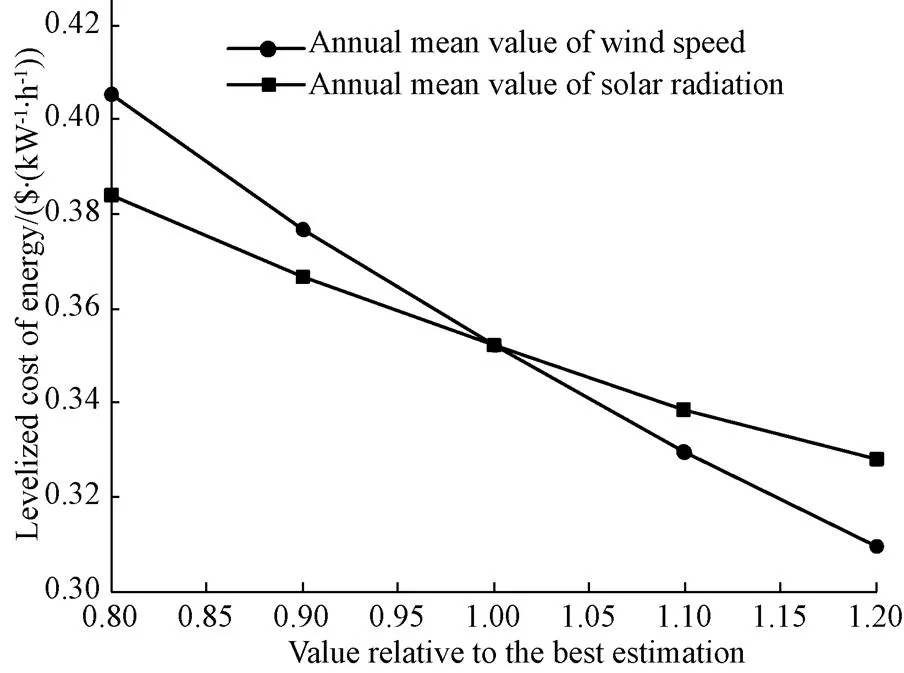
Fig.8 Effect of meteorological resources on the Levelized Cost of Energy (LCOE)
4 Conclusion
In this study, optimization of a stand-alone Hybrid Renewable Energy System (HRES) consisted of Wind Turbine (WT)-Photovoltaic (PV)-Battery System (BS) was focused and modeled as a single objective optimization problem. The objective function was to minimize the Levelized Cost of Energy (LCOE) while satisfying the reliability of the Loss of Power Supply Probability (LPSP). In order to get better optimization results, the Artificial Bee Colony algorithm with Differential Evolution operators (ABCDE) algorithm was introduced to solve the optimization problem. The effectiveness of ABCDE was validated by comparing test with Artificial Bee Colony (ABC) algorithm and Differential Evolution (DE) algorithm. Test results showed that ABCDE could achieve more accurate solutions and performed with better convergence speed and robustness. The results got by ABCDE showed that the optimal LCOE was 0.349 4 $/kWh while the LPSP was equal to 3% for the HRES. The relationship of LCOE and LPSP was obtained by changing the maximum allowable LPSP from 0 to 5% with an equal step of 0.1%. From the relationship, it could be seen that economy and reliability were contradictory indicators and the decline rate of LCOE was decreased gradually with the growth of LPSP. Sensitivity analyses for the initial capital of the main components and meteorological resources were also performed. Results showed that the LCOE was most sensitive to the PV initial capital in terms of equipment prices, and was more sensitive to annual mean value wind speed than that of solar radiation. This indicated that it should pay more effort to reduce PV initial capital and to improve the accuracy of wind resource assessment.
[1] Yang Yong, Guo Su, Liu Deyou, et al. Operation optimization strategy for wind-concentrated solar power hybrid power generation system[J]. Energy Conversion & Management, 2018, 160: 243-250.
[2] Kyritsis A, Voglitsis D, Papanikolaou N, et al. Evolution of PV systems in Greece and review of applicable solutions for higher penetration levels[J]. Renewable Energy, 2017, 109: 487-499.
[3] Anoune K, Bouya M, Astito A, et al. Sizing methods and optimization techniques for PV-wind based hybrid renewable energy system: A review[J]. Renewable & Sustainable Energy Reviews, 2018, 93: 652-673.
[4] Zahraee S M, Assadi M K, Saidur R. Application of artificial intelligence methods for hybrid energy system optimization[J]. Renewable and Sustainable Energy Reviews, 2016, 66: 617-630.
[5] Monaaf D A. A review on recent size optimization methodologies for standalone solar and wind hybrid renewable energy system[J]. Energy Conversion & Management, 2017, 143: 252-274.
[6] Nogueira C E C, Vidotto M L, Niedzialkoski R K, et al. Sizing and simulation of a photovoltaic-wind energy system using batteries, applied for a small rural property located in the south of Brazil[J]. Renewable & Sustainable Energy Reviews, 2014, 29(7): 151-157.
[7] Malheiro A, Castro P M, Lima R M, et al. Integrated sizing and scheduling of wind/PV/diesel/battery isolated systems[J]. Renewable Energy, 2015, 83: 646-657.
[8] Amrollahi M H, Bathaee S M T. Techno-economic optimization of hybrid photovoltaic/wind generation together with energy storage system in a stand-alone micro-grid subjected to demand response[J]. Applied Energy, 2017, 202: 66-77.
[9] Li Jianlin, Guo Binqi, Niu Meng, et al. Optimal configuration strategy of energy storage capacity in wind/PV/storage hybrid system[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1189-1196.
[10] HOMER Pro Version 3. 7 User Manual[Z], http: //www. homerenergy. com
[11] Zahboune H, Zouggar S, Krajacic G, et al. Optimal hybrid renewable energy design in autonomous system using modified electric system cascade analysis and homer software[J]. Energy Conversion & Management, 2016, 126: 909-922.
[12] Lambert T, Gilman P, Lilienthal P. Micropower System Modeling with HOMER[M]. Integration of Alternative Sources of Energy. John Wiley & Sons, Inc. 2006: 379-418.
[13] Shahzad M K, Zahid A, Rashid T, et al. Techno-economic feasibility analysis of a solar-biomass off grid system for the electrification of remote rural areas in Pakistan using HOMER software[J]. Renewable Energy, 2017, 106: 264-273.
[14] Halabi L M, Mekhilef S, Olatomiwa L, et al. Performance analysis of hybrid PV/diesel/battery system using HOMER: A case study Sabah, Malaysia[J]. Energy Conversion & Management, 2017, 144: 322-339.
[15] Rajbongshi R, Borgohain D, Mahapatra S. Optimization of PV-biomass-diesel and grid base hybrid energy systems for rural electrification by using HOMER[J]. Energy, 2017, 126: 461-474.
[16] Singh A, Baredar P, Gupta B. Techno-economic feasibility analysis of hydrogen fuel cell and solar photovoltaic hybrid renewable energy system for academic research building[J]. Energy Conversion & Management, 2017, 145: 398-414.
[17] Ghorbani N, Kasaeian A, Toopshekan A, et al. Optimizing a hybrid wind-PV-Battery system using GA-PSO and MOPSO for reducing cost and increasing reliability[J]. Energy, 2017, 154: 581-591.
[18] Singh S, Kaushik S C. Optimal sizing of grid integrated hybrid PV-biomass energy system using artificial bee colony algorithm[J]. IET Renewable Power Generation, 2016, 10(5): 642-650.
[19] Heydari A, Askarzadeh A. Techno-economic analysis of a PV/biomass/fuel cell energy system considering different fuel cell system initial capital costs[J]. Solar Energy, 2016, 133: 409-420
[20] Sharma S, Bhattacharjee S, Bhattacharya A. Grey wolf optimization for optimal sizing of battery energy storage device to minimise operation cost of microgrid[J]. IET Generation Transmission & Distribution, 2016, 10(3): 625-637.
[21] Ramli M A M, Bouchekara H R E H, Alghamdi A S. Optimal sizing of PV/Wind/Diesel hybrid microgrid system using multi-objective self-adaptive differential evolution algorithm[J]. Renewable Energy, 2018, 121: 400-411.
[22] Ogunjuyigbe A S O, Ayodele T R, Akinola O A. Optimal allocation and sizing of PV/Wind/Split-diesel/Battery hybrid energy system for minimizing life cycle cost, carbon emission and dump energy of remote residential building[J]. Applied Energy, 2016; 171: 153–171.
[23] Kamjoo A, Maheri A, Dizqah A M, et al. Multi-objective design under uncertainties of hybrid renewable energy system using NSGA-II and chance constrained programming[J]. International Journal of Electrical Power & Energy Systems, 2016, 74(1): 187-194.
[24] Sağ T, Çunkaş M. Color image segmentation based on multi-objective artificial bee colony optimization[J]. Applied Soft Computing, 2015, 34: 389-401.
[25] Li Xianneng, Yang Guangfei. Artificial bee colony algorithm with memory[J]. Applied Soft Computing, 2016, 41: 362-372.
[26] Li Junqing, Pan Quanke, Duan Peiyong. An improved artificial bee colony algorithm for solving hybrid flexible flow shop with dynamic operation skipping[J]. IEEE Transactions on Cybernetics, 2016, 46(6): 1311-1324.
[27] Zhang Xin, Zhang Xiu, Wang Lei. Antenna design by an adaptive variable differential artificial bee colony algorithm[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1-4.
[28] Karaboga D, Gorkemli B. A quick Artificial Bee Colony (qABC) algorithm and its performance on optimization problems[J]. Applied Soft Computing, 2014, 23: 227-238.
[29] Liang Zhengping, Hu Kaifeng, Zhu Quanxiang, et al. An enhanced artificial bee colony algorithm with adaptive differential operators[J]. Applied Soft Computing, 2017, 58: 480-494.
[30] Li Genghui, Lin Qiuzhen, Cui Laizhong, et al. A novel hybrid differential evolution algorithm with modified CoDE and JADE[J]. Applied Soft Computing, 2016, 47: 577-599.
[31] Opara K, Arabas J. Comparison of mutation strategies in differential evolution-A probabilistic perspective[J]. Swarm & Evolutionary Computation, 2018, 39: 53-69.
改进人工蜂群算法的孤岛混合可再生能源发电系统容量优化
杨 勇1,2,李 荣1,2※,郭 苏2,刘德有2
(1. 南京工程学院能源与动力工程学院,南京 211167;2. 河海大学水利水电学院,南京 210098)
容量优化对提高风电-光伏-电池混合发电系统的经济性和可靠性具有重要意义。为进一步提高容量优化的精度,本研究提出了一种基于改进蜂群算法的容量优化方法。首先,在建立组件模型、设计能源管理规则库的基础上,以最小化单位度电成本为目标,以系统缺电率为约束,建立了混合发电系统容量优化模型;其次,通过在蜂群算法雇佣蜂阶段中引入差分进化算子,提出了一种改进蜂群算法的模型求解方法,并通过与蜂群、差分进化算法对比,验证了改进蜂群算法的有效性;最后,分别在不同缺电率要求下优化混合系统容量,得出了单位度电发电成本与缺电率的关系,并通过灵敏度分析,研究了设备价格,气象等因素对单位度电成本的影响。结果表明,在缺电率为3%时,混合系统总投资成本为779 564.26 美元($), 其中,光伏、风电、电池及变换器成本分别占总成本的33%、29%、34%和3%,单位度电成本为0.349 447 $/kWh;单位度电成本随缺电率增加而下降且下降速率逐渐降低;单位度电成本在组件价格方面受光伏组件价格影响更明显,在气象方面,受风速均值影响更明显。该研究成果可为科学设计混合系统容量,促进风、光资源互补利用提供科学依据。
可再生能源;优化;算法;混合发电系统;人工蜂群算法;差分进化算子;容量优化;灵敏度分析
Yang Yong, Li Rong, Guo Su, et al. Optimizing the capacity of standalone hybrid renewable energy power generation system by improved artificial bee colony algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(15): 217-226. (in English with Chinese abstract)doi:10.11975/j.issn.1002-6819.2020.15.027 http://www.tcsae.org
杨勇,李荣,郭苏,等. 改进人工蜂群算法的孤岛混合可再生能源发电系统容量优化[J]. 农业工程学报,2020,36(15):217-226. doi:10.11975/j.issn.1002-6819.2020.15.027 http://www.tcsae.org
2019-12-05
2020-04-20
Natural Science Foundation of China (51706093); Natural Science Foundation of Jiangsu Province (BK20181308); Fundamental Research Funds for the Central Universities (2018B45414)
Yang Yong, PhD, Lecturer, research interests: hybrid system capacity optimization. Email:542450062@qq.com
Li Rong, PhD, Lecturer, research interests: hybrid power generation system scheduling. Email:njit_lr@njit.edu.cn
10.11975/j.issn.1002-6819.2020.15.027
TK83
A
1002-6819(2020)-15-0217-10
