ZnX3(OH)6Cl2(X=Co, Ni)声子谱和热力学性质的第一性原理研究
2020-09-18董欣月冯敏王玉芳
董欣月,冯敏,王玉芳
(南开大学物理科学学院,天津 300071)
1 引言
ZnCu3(OH)6Cl2是以矿物学家Herbert Smith的名字命名的一种稀有矿物,与之相关的材料研究最早来源于1906年他描述的Cu4(OH)6Cl2[1]。2005年由Shores 等人通过水热法合成[2]。它的合成引起了众多物理学家的关注,引发人们在Kagome海森堡反铁磁晶格上寻找新的量子自旋液体(QSL),进而开展了大量的理论计算和实验研究[3,4]。在所有的无机自旋液体候选材料当中,它几乎是完美的自旋1/2 Kagome格子[5],这种量子自旋液体材料具有强烈的几何阻挫和量子涨落,即使在温度低于50 mK下,仍然不能出现自旋有序的排布[6-8]。
ZnCu3(OH)6Cl2的晶体结构、电子结构、磁性以及晶格振动模式等的研究已有相关报道[9,10]。但是目前量子自旋液体种类不多,寻找新的材料研究有待开展。Co,Ni,Cu均为主要过渡金属元素,在元素周期表中相邻排布,因此本文所要研究的是,将低自旋1/2的铜离子替换为自旋分别为3/2和1的钴离子和镍离子,对其晶体结构、晶格振动属性进行计算,进而分析比较对称性、频率及热力学性质。为寻找新材料在理论上预测,试图寻找到新的量子自旋液体材料。
2 晶体结构和计算方法
ZnCo3(OH)6Cl2和ZnNi3(OH)6Cl2晶体对称性属于166号空间群(R-3m),图1(a)给出了ZnCo3(OH)6Cl2晶胞的晶体结构,一个晶体结构单元中有54个原子,磁性钴原子位于层内形成的Kagome格子上。由图可以看出非磁的锌离子位于两层Kagome格子之间。固体物理学原胞如图1(b)所示,原胞中共含有18个原子,1个Zn原子,3个Co原子,6个O原子,6个H原子,2个Cl原子,且该图清晰地展现了钴离子形成的Kagome格子。在面内,每个磁性离子有4个最近邻和4个次近邻,形成不同的耦合强度。
本文采用基于密度泛函理论[11]的平面波赝势方法,用赝势代替离子势,电子波函数用平面波基组展开,采用周期性边界条件,平面波数目由截断能决定,总能量计算采用自洽迭代方法(scf);电子与电子相互作用的交换关联能采用广义梯度近似(GGA)下的PBE泛函[12],价电子与芯电子间相互作用采用投影缀加平面波(PAW)赝势。
第一性原理对声子结构计算,主要有冷冻声子法(frozen-phonon)[13]和密度泛函微扰理论(Density Density Perturbation Theory),即DFPT[14]。前者对于简单晶体结构计算准确,而对于复杂结构,需要很大的超胞,因而对计算条件要求较高。相比于直接方法,DFPT方法则通过系统对外界能量的响应求解声子谱,能适应于复杂体系。因此我们采用DFPT方法,计算软件为VASP[15]结合PHONOPY[16]。
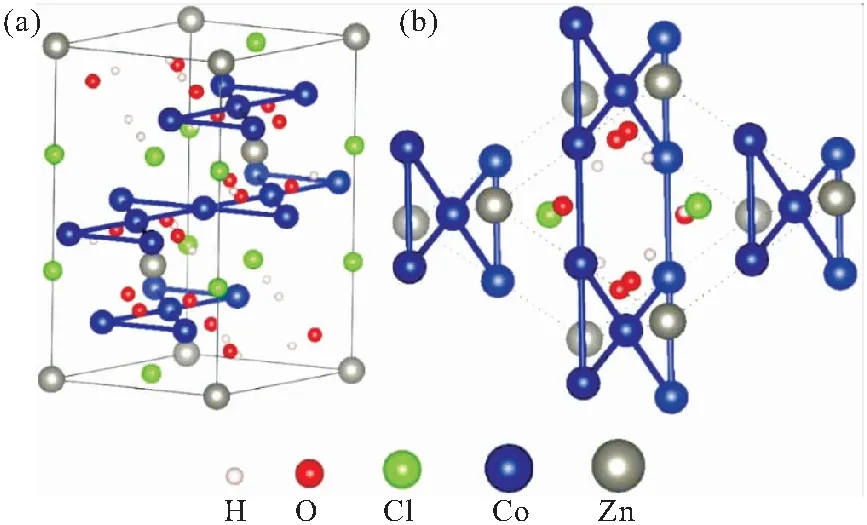
图1 ZnCo3(OH)6Cl2: (a)晶胞; (b)原胞以及Co离子形成的Kagome格子
在利用Vasp软件计算时,首先对晶体进行结构优化,使其达到稳定结构。原胞优化过程中体系总能量和力的收敛标准分别设置为10-7eV和10-3eV/Å,截断能设置为520 eV,k网格设置为11×11×11,各个原子的赝势均采用标准形式。在优化时先采用共轭梯度方法搜索稳定结构的大致范围,再选用准牛顿方法继续优化,直至收敛到设置的精度范围。之后建立一个2×2×2的超胞,计算出Hessian矩阵,再利用PHONOPY软件计算出力常数,然后基于力常数文件对两种材料声子谱、声子模式密度进行计算,并进一步分析晶体对称性、频率及热力学性质。
3 结果与讨论
3.1 声子谱与声子态密度计算
三种化合物结构优化后的晶格参数如表1所示,为了更好地比较ZnX3(OH)6Cl2(X=Co, Ni)优化后的晶格参数变化,首先对ZnCu3(OH)6Cl2进行了结构优化,其晶格常数及α角的理论计算值分别为6.131 Å和70.116°,而实验值分别为6.119 Å和67.892°。计算结果与实验值的差别为0.20%和3.17%。以ZnCu3(OH)6Cl2的理论计算值作为参考,优化后的ZnCo3(OH)6Cl2的晶格常数和α角分别变大和变小,ZnNi3(OH)6Cl2的晶格常数和α角均变小。
晶格振动的声子谱,即格波的角频率与波矢量的关系曲线。通过使用DFPT方法计算得到两种材料的声子在布里渊区特殊点Γ(0,0,0)、L(0.0,0.5,0.0)、Z(0.5,0.5,0.5)、F(0.5,0.5,0.0)上的频率值,给出了声子色散及态密度曲线,分别如图2和图3所示。由于固体物理学原胞有s=18个原子,共有54条声子谱曲线,有3支声学支格波,3s-3支光学支格波。计算结果与理论相一致。从声子谱的结果看没有虚频,说明两种结构是稳定的。Γ点处最低的三条曲线位于声学频率范围内,即是声学支格波,其余为光学支格波。长波极限情形下,声学支格波反映原胞内原子以相同的振幅和相位做整体运动,代表原胞质心的振动;而光学支格波代表原胞中粒子的相对振动,原胞的质心保持不动。从声子态密度的结果看出,ZnCo3(OH)6Cl2和ZnNi3(OH)6Cl2分别在频率为146 cm-1和149 cm-1处声子态密度最大。声子谱光学支的低频部分主要来源于O、Co/Ni、Cl、H原子,光学支高频部分来源于H、O原子贡献。

表1 优化后三种化合物晶格常数和α角的比较
图2 ZnCo3(OH)6Cl2:(a)声子谱; (b)态密度

图3 ZnNi3(OH)6Cl2:(a)声子谱; (b)态密度
3.2 拉曼活性振动模式的对称性和频率
为了确定拉曼活性振动模式,且能更好的与ZnCu3(OH)6Cl2作比较,首先对其计算了拉曼峰位,并与实验结果[17]进行了对比。晶格振动模式及6个主要的拉曼峰位与实验对比结果分别如下表2和表3所示。
ZnCu3(OH)6Cl2原胞中有18个原子,在Γ点会产生54支格波,3支声学波(Γacoustic)和51支光学波(Γopt)。通过计算得到的每个振动模式的本征位移可以清楚地得到每个声子振动模的振动形式。由振动分析知,三支声学波代表所有原子在三个自由度上整体作平移运动,其他光学支为晶体的基本振动。下面计算了ZnX3(OH)6Cl2(X=Cu, Co, Ni) 的所有拉曼活性振动模式,如表4所示。

表2 ZnX3(OH)6Cl2(X=Cu,Co,Ni)系统的振动模式分析

表3 ZnCu3(OH)6Cl2的布里渊区Γ点拉曼峰位的计算值和实验值比较

表4 ZnX3(OH)6Cl2(X = Cu, Co, Ni)在布里渊区Γ点拉曼峰位的计算值
图4为ZnCo3(OH)6Cl2的6个与ZnCu3(OH)6Cl2相对应的主要拉曼峰的振动情况,可分为三个区间:低频区(200~300 cm-1),中频区(300~500 cm-1),高频区(600~900 cm-1)。其中低频支264 cm-1的振动由H、O原子贡献,振动方向与kagome格子平面成一定角度,且两种原子贡献均较大。同样由这两种原子贡献的还有高频支的673 cm-1和861 cm-1,在673 cm-1时,部分O原子在垂直于kagome平面振动,但振幅相对于H原子较小;在861 cm-1的模式,所有O原子均在垂直于kagome平面振动,振幅相对H原子仍然较小,H原子的振动形成一个类似呼吸模。其余三个中频支振动均由H、O、Cl原子贡献,H、O原子振幅大小基本一致,Cl原子的振幅明显要小。其中频率为403 cm-1的A1g模中三种原子振动方向均垂直于kagome平面;频率为442 cm-1中的Cl原子振动方向平行于kagome平面,H、O原子均与该平面成一定角度;在491 cm-1的频率下,Cl原子垂直于kagome平面,O、H原子形成一个呼吸模。接下来对ZnNi3(OH)6Cl2进行了同样的计算,在对应频率243 cm-1、375 cm-1、462 cm-1、525 cm-1下均由H、O、Cl原子贡献,且Cl原子的振幅小于H、O;高频支的813 cm-1下由H和部分O原子的振动贡献,而972 cm-1频率下,O原子不再参与振动,只由H原子的振动来贡献。我们看到以上模式都没有涉及到磁性离子Co、Ni、Cu的振动,对计算结果的分析显示这三种离子参与的振动模式都不具备拉曼活性,其中12种具备红外活性的振动频率,总结在表5中。
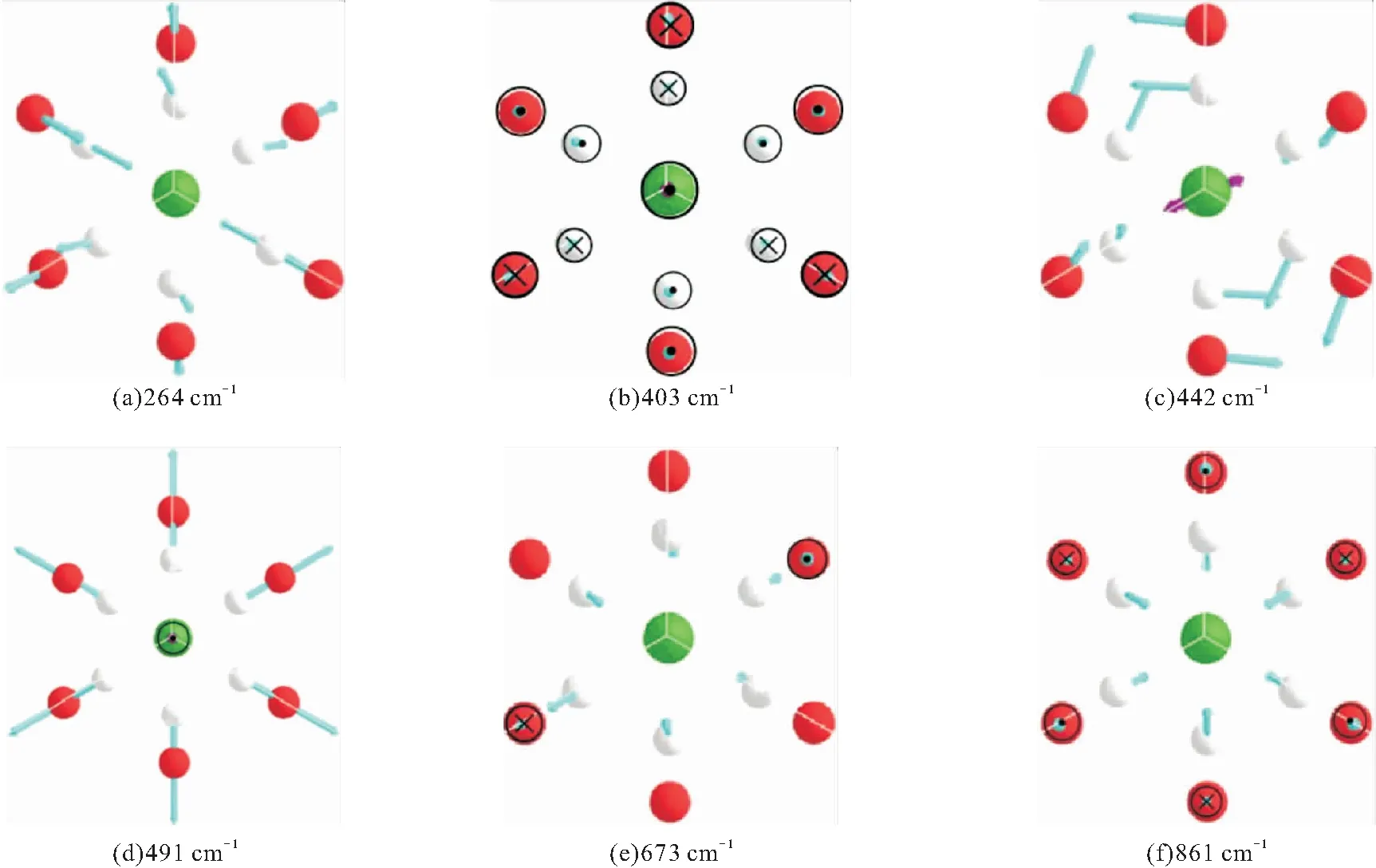
图4 ZnCo3(OH)6Cl2主要拉曼峰的振动模式(白色:H,红色:O,绿色:Cl;垂直纸面向里,⊙垂直纸面向外)

表5 ZnX3(OH)6Cl2(X = Cu, Co, Ni)中有磁性离子Co、Ni、Cu参与的红外频率
3.3 热力学性质分析
图5给出了ZnX3(OH)6Cl2(X=Co, Ni)声子振动自由能、熵、定容摩尔热容和内能随温度变化的曲线。从图中可以看出熵、定容摩尔热容和内能随温度的升高而增大,声子振动自由能随温度的升高而减小。熵描述热力学系统的混乱程度,故随着温度升高,熵会相应增加。在0~200K的范围内,晶体的定容摩尔热容几乎呈线性增加,200K~400K之间,增速减慢,600K之后趋于一个定值。
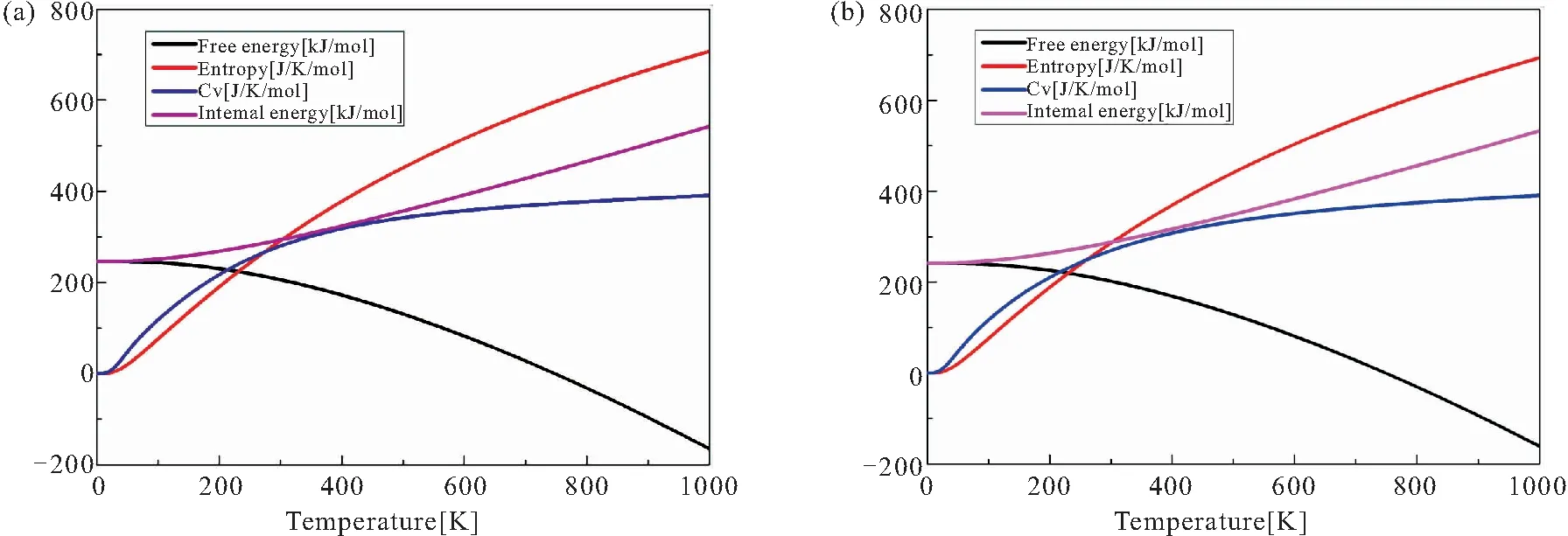
图5 (a)ZnCo3(OH)6Cl2和(b) ZnNi3(OH)6Cl2的热力学性质
4 结论
ZnX3(OH)6Cl2(X=Co, Ni)的声子谱计算结果显示没有虚频,由此判定该结构可以稳定存在;从声子态密度可以看出,光学支的低频部分主要由O、Co/Ni、Cl、H贡献,高频支部分由H和O贡献;通过对晶格振动模式的分析找到了拉曼峰的位置,得出了ZnCo3(OH)6Cl2中与ZnCu3(OH)6Cl2的6个主要拉曼峰对应的振动模式。计算对比了ZnX3(OH)6Cl2(X = Cu, Co, Ni)中有磁性离子参与的12种红外频率;计算和分析的热力学性质符合物理规律。
