脉动流量下涡轮流量计动态特性流体仿真研究

张永胜，于小丽，刘彦军

（航空工业北京长城计量测试技术研究所，北京100095）

0 引言

涡轮流量计是典型的速度式流量计［1-2］，通过测量叶轮的转速来计算管道中流体体积流量。稳定流动下涡轮流量计具有重复性好、量程范围宽、适应性强、精度高、体积小等特点。但在工业领域的流量测量中，非稳态流动工况广泛存在，如脉动流量。脉动流量可由旋转式、往复式或其他可运动传送设备而产生，脉动流动一旦形成就会在流体中传播，将会对涡轮流量计产生较大的影响［3］。其脉动幅度和脉动频率的变化均会对涡轮流量计动态特性产生一定的影响。频率低、幅度小的脉动流，一般情况下对流量测量影响不大，但若脉动频率较高或幅度较大时则将对流量计的幅频特性和相频特性产生很大影响。

研究中利用CFD软件对涡轮流量计在正弦脉动流动下的流场进行仿真计算，获得不同脉动频率和幅度下涡轮流量计角速度曲线，进而计算瞬时流量，对涡轮流量计动态特性进行分析研究。

1 涡轮流量计建模

1.1 几何模型

研究中针对DN32口径的液体涡轮流量计展开，其机芯内部结构如图1所示，主要包括前后导向件和叶轮三部分。对涡轮流量计实物的外形尺寸和位置关系等关键尺寸进行测绘（表1为涡轮流量计主要尺寸参数），忽略流量计进出口连接形式等次要因素的影响，绘制三维结构图如图2所示。

图2 涡轮流量计三维模型

表1 流体仿真拟合系数表

1.2 流体仿真模型

利用Gambit软件进行几何建模和网格划分，为使流动在流量计入口处达到充分发展的流动状态，分别在流量计的上游设置10倍长直管段，下游设置5倍直管段。将叶轮所在区域定义为旋转区域，其余部分定义为静止区域，通过interface面将动静区域进行连接。旋转区域及结构较复杂的区域采用非结构化网格；直管段等结构较简单的区域采用结构化网格。

仿真中选用Reynolds Stress（S-BLS）湍流模型，该模型是最符合物理现象的模型，各向异性，输运中的雷诺应力可直接计算出来。模型计算时间较长，适合大弯曲流线、漩涡以及三维转动流动。选用RP-3航空煤油作为流体介质，以实测介质密度和粘度并设置仿真流体参数。设置下游直管段出口为自由出流（outflow）条件，直管段及流量计壳体为静止壁面（wall）；上游直管段入口为速度入口（velocity-inlet）。

1.3 仿真方法

涡轮流量计叶轮受到流体冲击时，对叶轮产生驱动力矩，同时受到各种阻力矩的影响［4-8］，图3是叶轮所受力矩示意图。叶轮转动过程中受到流体对叶片的驱动力矩Td，轮毂侧面受到流体粘性阻力矩Th，轮毂端面受到流体粘性阻力矩Tw，叶片顶端受到流体粘性阻力矩Tt，同时叶片轮轴与轴承之间存在机械阻力矩Tb，磁电信号检出器产生磁电阻力矩Tm。

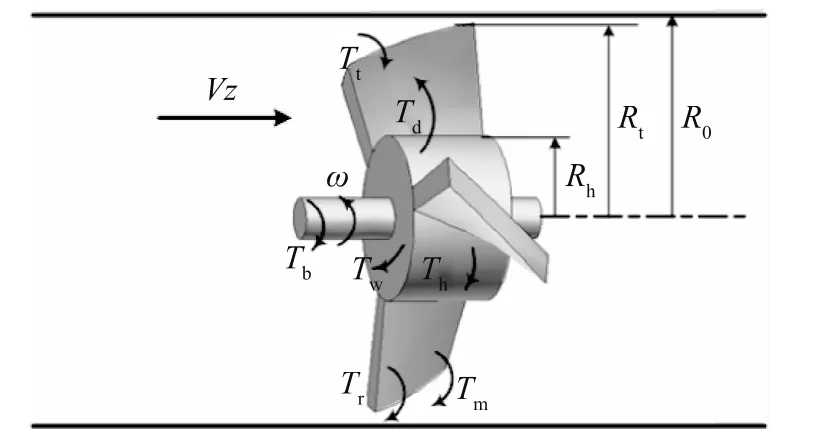
图3 叶轮所受力矩分析

叶轮的运动微分方程为

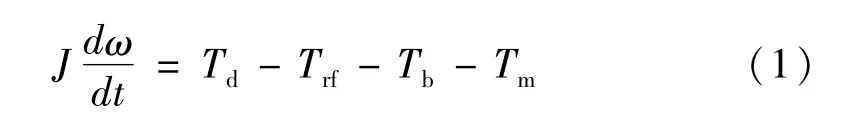
式中:J为叶轮转动惯量；ω为叶轮转动角速度；t为运行时间；Trf为流体阻力矩，Trf=Th+Tw+Tt。

采用6DOF模型实现对叶轮6个自由度的控制，包括X，Y，Z方向的移动自由度和围绕X，Y，Z轴的旋转自由度。通过DEFINE_SDOF_PROPERTIES宏文件约束叶轮在X，Y，Z方向上的移动以及围绕X，Y轴的旋转，只能围绕Z轴（流动方向）进行转动。叶轮三维建模中选用的材质与实际材质相同，即可获得叶轮的转动惯量。流体仿真中系统自行计算流体驱动力矩、流体阻力矩，忽略轴承摩擦阻力矩和磁电阻力矩。

仿真中通过UDF函数对上游直管段入口流速进行设置，流速通过式（2）和式（3）计算。

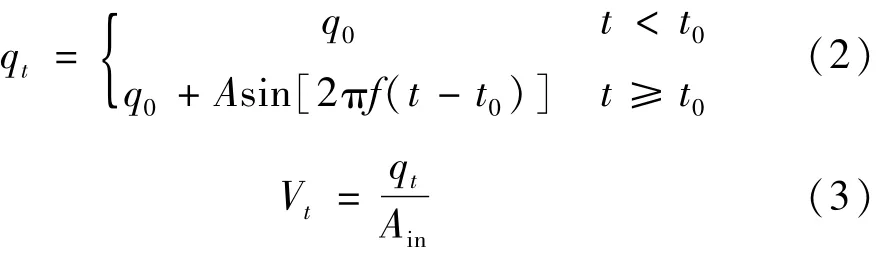
式中:qt为入口瞬时体积流量；q0为体积流量平均值，q0=16 m3/h；A为脉动幅度；f为脉动频率；t0为脉动流量起始时刻，t0=0.0132 s；Vt为瞬时入口速度平均值；Ain为上游直管段入口截面积。

仿真初始叶轮转速为零，根据叶轮运动方程自动计算和调整旋转角速度，直到叶轮趋于稳定状态，仿真中各工况在t0前叶轮转速已经达到稳定状态。

采取SPSS21.0进行数据处理，计数资料以（%）表示，计量资料以（±s）表示，分别行χ2或t检验；P＜0.05表示差异有统计学意义。

2 仿真结果与试验验证

仿真计算中调整脉动幅度（A=5，10，15，20 L/min）和脉动频率（f=5，10，15，20，30，40，50 Hz）两参数设置，计算28个不同工况下流场，获得叶轮转速随时间变化曲线，图4时脉动频率为20 Hz和50 Hz时的叶轮转速曲线。

待流量计叶轮旋转平稳后，取t0时刻前的叶轮转速通过式（4）计算仪表系数。

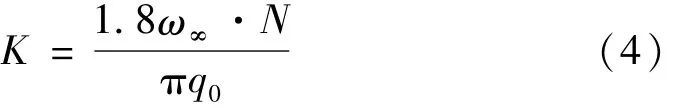
式中:K为仪表系数，L-1；ω∞为稳定叶轮转速，rad/s；N为涡轮叶片数量，N=6；q0为入口平均流量，m3/h。

经计算DN32涡轮流量计在16 m3/h流量下，仪表系数K=160.6 L-1。依据JJG 1037-2008《涡轮流量计检定规程》［9］，利用流量标准装置对涡轮流量计进行校准试验，获得16 m3/h流量下仪表系数K=161.7 L-1，与仿真结果的仪表系数相差仅0.7%，仿真与校准试验一致性非常好。

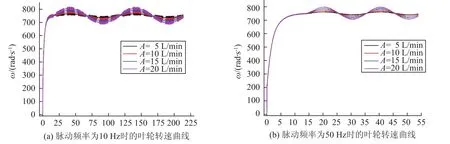
图4 涡轮流量计转速曲线

3 动态特性分析

涡轮流量计瞬时输出流量可由式（5）计算。

式中:qm为涡轮流量计瞬时流量，m3/h；ω为叶轮瞬时转速，rad/s。

由于流量计前后导流件的作用，导致叶轮转速和流量计瞬时流量存在小幅波动，图5是f=40 Hz涡轮流量计瞬时流量曲线，通过正弦函数对流量计瞬时流量进行拟合，拟合函数为

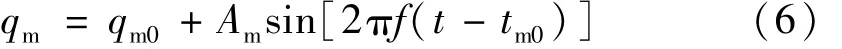
式中:qm0为流量计输出瞬时流量平均值，m3/h；fm为流量计输出脉动频率，Hz；Am为流量计输出脉动幅度；tm0为流量计输出脉动流量起始时刻，s。

仿真中28组工况拟合结果决定系数都大于0.995，拟合效果非常好，拟合获得了各工况涡轮流量计输出流量的平均值qm0、脉动频率fm、脉动幅度Am和脉动起始时刻tm0四个参数。流量计输出幅频特性和相频特性分别通过式（7）和式（8）计算。

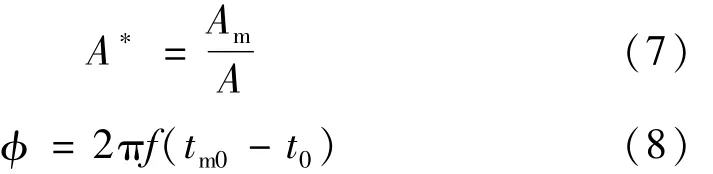
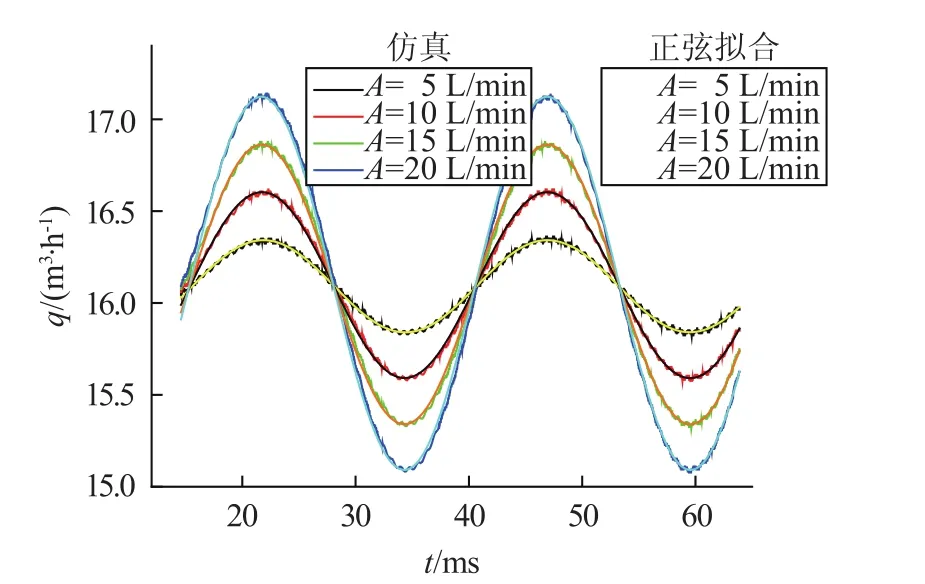
图5 40 Hz涡轮流量计瞬时流量曲线

将各工况正弦拟合曲线作为动态输出，与入口瞬时流量进行比较，图6是脉动频率分别为5，50 Hz时涡轮流量计动态信号曲线图，可见脉动幅值对相位差基本无影响。各工况流量计输出流量的平均值比较恒定，变化范围是16.079～16.094 m3/h，比输入流量平均值偏大不足0.6%。图7是涡轮流量计幅频特性与相频特性曲线图。A*随脉动频率f基本成线性降低的趋势，低频情况下A*≈1，且略大于1；随脉动频率增加，A*逐渐减小，在f=50 Hz时A*≈0.8。对于相位差而言，在f＜40 Hz的范围内，相位差随脉动频率增加而增大，相位差由3.7°～4.8°增大至20.9°～24.2°；在f=40 Hz之后，相位差趋于平稳。叶轮是涡轮流量计内的唯一可动部件，叶轮在流体驱动力矩和阻力矩作用下产生加速度，由于叶轮自身转动惯量的影响，导致叶轮角速度变化滞后于流量脉动流动变化，产生流量示值与真实之间的相位差，而相位差受到流量计自身时间常数和流量脉动输入双方面的综合影响，涡轮流量计一般认为是一阶非线性系统［10］，其时间常数是随流量输入而改变的。

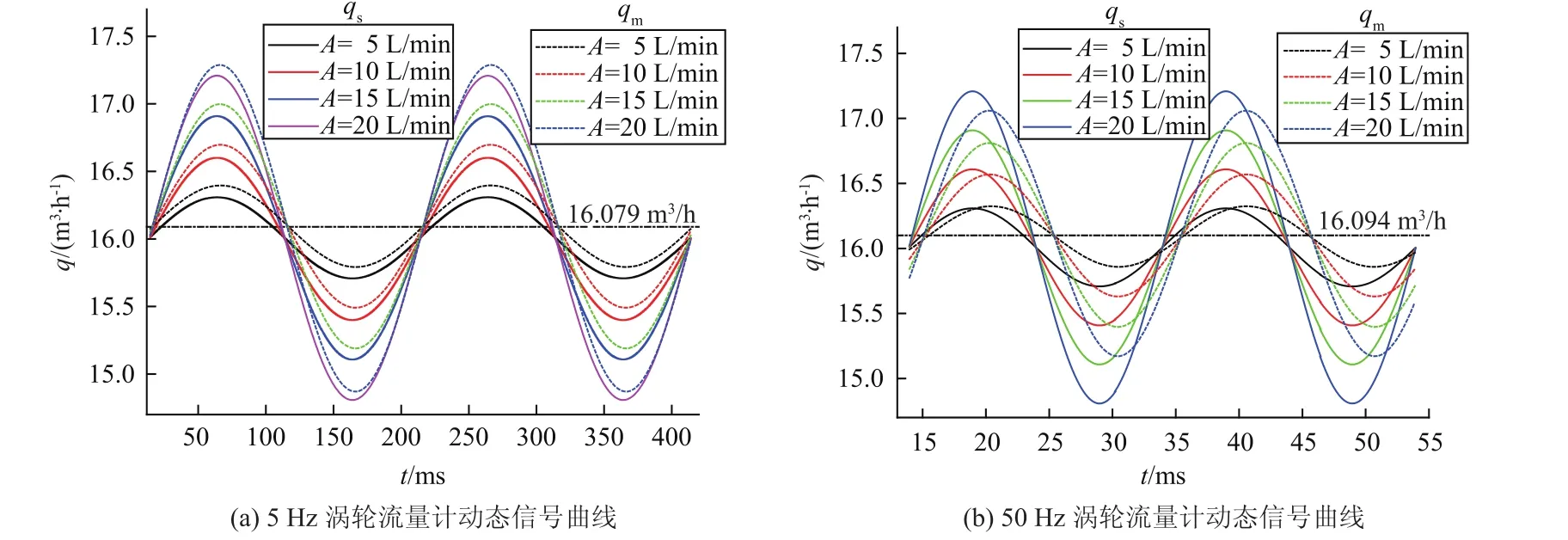
图6 涡轮流量计动态特性曲线

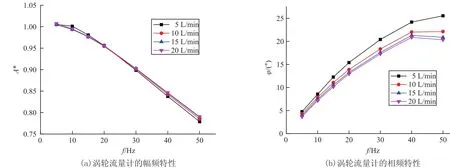
图7 涡轮流量计幅频特性和相频特性

4 结论

研究中利用FLUENT软件中的6DOF模型对DN32口径涡轮流量计进行流体仿真，仿真过程中改变入口流量脉动幅值和脉动频率，共获得28组工况脉动流动下的流场。分析获得叶轮转速随时间变化曲线，并利用正弦函数对流量计输出进行拟合，获得流量计瞬时流量的平均值、脉动幅值和初始相位等参数，进一步获得了流量计幅频特性和相频特性。各工况流量计输出流量平均值可认为是定值，幅频特性随脉动频率成线性降低的趋势，而相频特性受到涡轮流量计时间常数和脉动输入综合影响，在f＜40 Hz的范围内随频率增加而增加，在f=40 Hz之后，相频特性趋于平稳。

本仿真研究中，涡轮流量计规格单一且工况较少，未来还需要结合理论分析、实流试验、流体仿真等多种手段对涡轮流量计在脉动流动下动态特性开展研究，进一步探究涡轮流量计动态响应机理和修正方法，提高涡轮流量计在脉动流量测量中的准确度。