激光标线仪校准方法的探讨

金挺，梁琦，王瑛辉

（1.浙江省计量科学研究院，浙江杭州310018；2.广西壮族自治区计量检测研究院，广西南宁530007）

0 引言

激光标线仪又称为激光投线仪或激光墨线仪，是一种可以提供水平标线和铅垂标线的激光仪器，可代替传统的水平管、铅锤球、墨线等，应用于建筑施工、装饰装潢等领域。随着我国经济建设的快速发展，各类精度高、方便实用的小型测量工具越来越被广大用户所接受。手持式激光测距仪、激光扫平仪、激光垂准仪、激光标线仪等均属于近几年新兴的实用测量工具，在国内外建筑和装饰工程中被广泛采用。目前国内有一部分计量技术机构和科研院校的专业技术人员对激光标线仪检测方法进行了一定的研究，但由于在计量参数的选择、校准装置的设计和测量方法等方面存在一定的差异［1-5］，导致目前国内还没有形成统一的计量规范。本文针对这种情况，结合激光标线仪在制造和应用过程中的技术特性，提出了独立的观点及解决方法。

1 激光标线仪工作原理

如图1所示，激光标线仪的工作原理:半导体激光器发出的光束垂直照射到柱状透镜上，出射后将得到一个与柱状透镜垂直的扇形平面，该扇形平面照射到平面上将得到一条激光直线。柱状透镜铅垂放置，将得到水平的激光线，柱状透镜水平放置，将得到铅垂的激光线［6-7］，如图2所示。

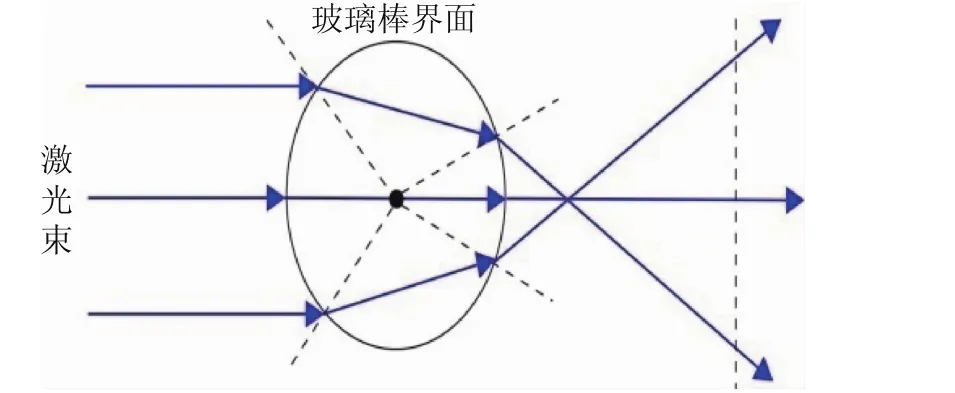
图1 激光标线仪工作原理图

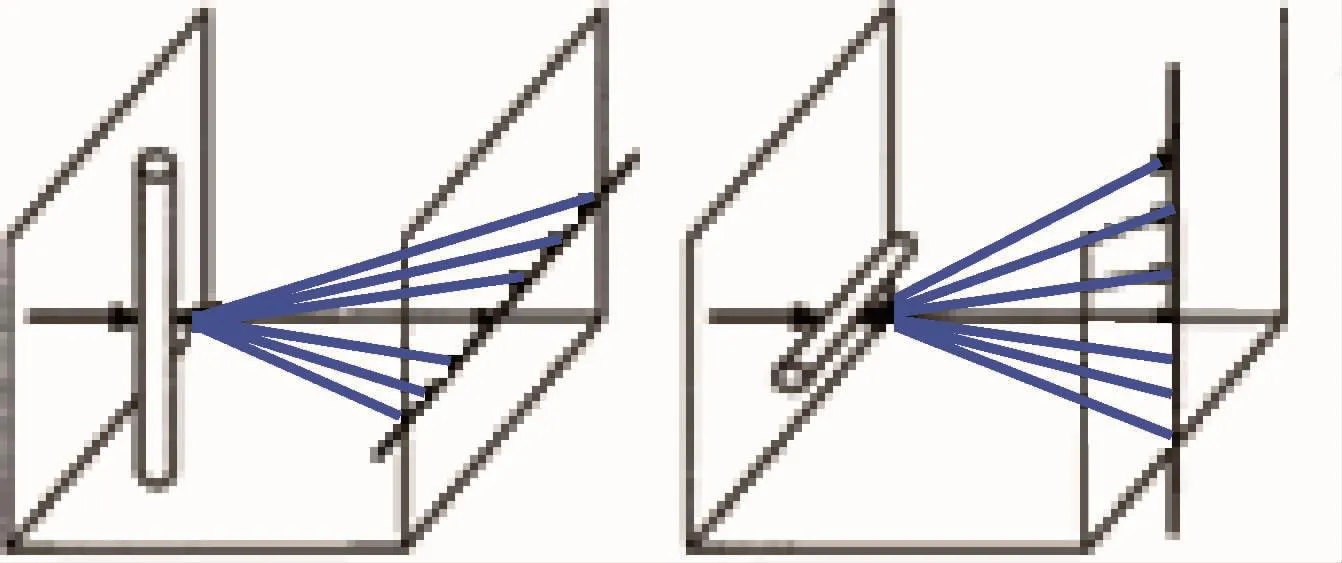
图2 激光标线仪投影线示意图

2 激光标线仪发展现状

我国是全球激光标线仪最大的生产制造基地，国内外市场占比超过百分之九十。激光标线仪种类繁多，根据应用场合和测量对象的不同其结构功能设计也有所不同，主要有以下几种类别:

1）按照产品安平结构可分为重力摆结构和电子自动安平结构两种形式；

2）按照产品激光线条数可分为1V1H，2V1H，3V1H，4V1H，4V2H，4V3H，4V4H等系列（其中，V代表垂直激光线，H代表水平激光线）；

3）按照激光颜色可分为红光和绿光两种；

4）按照激光线的张角可分为120°和360°等，如水平激光线张角为360°，垂直激光线张角为120°时，可分为1V360°H，2V360°H，3V360°H，4V360°H；当激光线张角均为360°时，一般只有3D，2D两种仪器，3D为两个互相垂直的铅垂面和一个水平面，2D为一个铅垂面和一个水平面。

3 校准方法

根据激光标线仪的工作原理，可将其主要计量特性分为“水平激光线误差”，“水平激光线近、远端倾斜误差”，“水平激光线补偿误差”，“垂直激光线误差”，“垂直激光线间的正交误差”，“下对点误差”，“天顶点误差”等。其中“下对点误差”和“天顶点误差”的校准方法相对简单，与经纬仪和垂准仪的校准方法相近，因此在本文中暂不作介绍。

3.1 校准装置的设计

由于激光标线仪具有水平激光线和垂直激光线相关参数，因此要求其校准装置在水平方向和垂直方向上均能进行测量。

水平激光线校准装置如图3所示。考虑到工作距离L2引入的激光线宽和读数分辨力等因素对测量结果的影响，建议在工作距离5～10 m处安放远点直角坐标板2，3，4，另外在距离工作台轴心L1=0.5～1 m处安放一个近点直角坐标板1，用于测量水平激光线近、远端倾斜误差。考虑到激光线的张角，一般要求直角坐标板2，4与直角坐标板3之间的夹角ω为30°～60°，建议设计为45°。同时要求所有直角坐标板的原点等高，并且确保所有直角坐标板的原点处于同一水平面内。

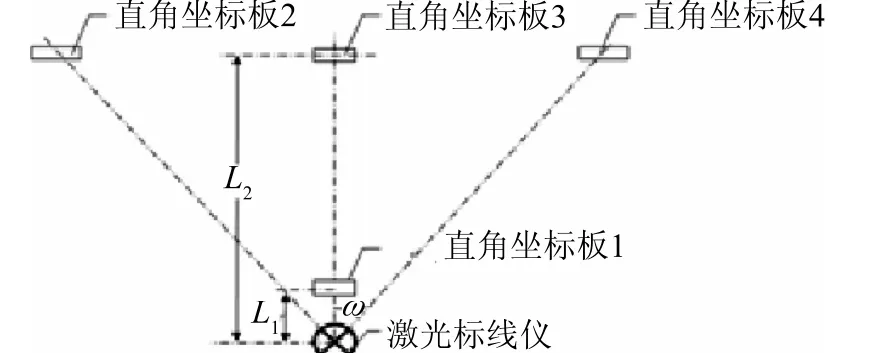
图3 水平激光线误差校准装置示意图

垂直激光线校准装置如图4所示。其工作距离L以及直角坐标板1，3与直角坐标板2之间的夹角ω的选取与水平激光线校准装置一致，建议取L=5～10 m，ω=45°。由于标线仪垂直激光线发射筒轴线与水平面间存在一个向上的倾角θ（约为15°～35°），因此在设计安装时要求直角坐标板2与水平面间的夹角为θ。同时要求所有直角坐标板的原点均处于同一个平面内，并且该平面与水平面垂直。

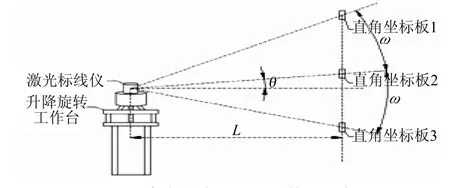
图4 垂直激光线误差校准装置示意图

3.2 误差来源分析及测量方法

3.2.1 水平激光线误差

水平激光线误差是指激光标线仪所发出的水平激光扇形面在铅垂面上的投影线偏离水平线的最大夹角。

依照图3所示，将被检仪器放置在工作台上，调平工作台并整平仪器，使被检仪器的水平激光线的中间部分照准近点直角坐标板1的原点。待激光稳定后，读取激光线在每个直角坐标板上的读数Δi（i=1，2，3，4）。重新安置仪器，并按上述方法重复测量三次，分别计算直角坐标板1，2，3，4上的读数平均值（单位为mm），然后将远点直角坐标板3与被检仪器中心的距离 L2（单位为 mm）代入公式（1）［8］，换算得到10 m位置的偏差值，即为水平激光线误差Δ平，单位为mm。

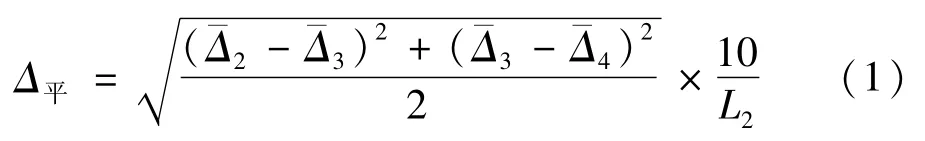
升降工作台，调整仪器高度，依次校准其它水平激光线。

3.2.2 水平激光线近、远端倾斜误差

水平激光线近、远端倾斜误差是指激光标线仪所发出的水平激光扇形面与水平面间的夹角。该误差的测量原理与水准仪i角误差的测量原理类似。

依照图3所示，按3.2.1的方法进行测量，水平激光线近、远端倾斜误差δ。

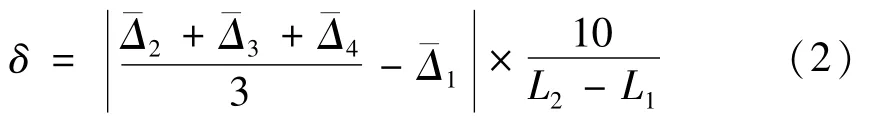
3.2.3 水平激光线补偿误差

水平激光线补偿误差是指在激光标线仪补偿范围内，标线仪发生倾斜时水平激光线近、远端倾斜误差的变化量。

将标线仪分别右倾、左倾、后倾、前倾2.5°，依照3.2.2的方法分别测出各方向倾斜时的水平激光线近、远端倾斜误差δR，δL，δB，δF，取其与标线仪水平安置时的水平激光线近、远端倾斜误差δ差值绝对值的最大值作为测量结果。

3.2.4 垂直激光线误差

垂直激光线误差是指激光标线仪所发出的垂直激光扇形面在铅垂面上的投影线偏离铅垂线的最大夹角。

依照图4所示，将被检仪器放置在工作台上，调平工作台并整平仪器，使被检仪器的垂直激光线照准直角坐标板2的原点。待激光稳定后，读取激光线在每个直角坐标板上的读数Δi（i=1，2，3）。重新安置仪器，按上述方法重复测量三次，分别计算直角坐标板1，3的读数平均值对应直角坐标板2与被检仪器中心的距离L，按照公式（3）换算到10 m位置的偏差值，即为垂直激光线误差Δ垂。

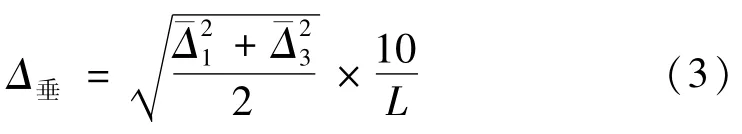
旋转仪器，依次校准其它垂直激光线。

3.2.5 垂直激光线间的正交误差

垂直激光线间的正交误差是指相邻垂直激光扇形面间的夹角与90°的差值。

依照图4所示，将被检仪器放置在旋转工作台上，整平仪器，将一条垂直激光线照准直角坐标板1的原点，读取相邻激光线在另一直角坐标板3上的读数。重新安置仪器，按上述方法重复测量三次，计算平均值，对应直角坐标板2与被检仪器中心的距离L，换算得到10 m位置的偏差值，作为垂直激光线间的正交误差。

4 不确定度分析

本文以水平激光线误差为例进行不确定度评定，垂直激光线误差的来源和不确定度评定方法与水平激光线误差基本相同。

4.1 数学模型

水平激光线误差按照公式（1）计算，当取距离L2=10 m，公式（1）可简化为

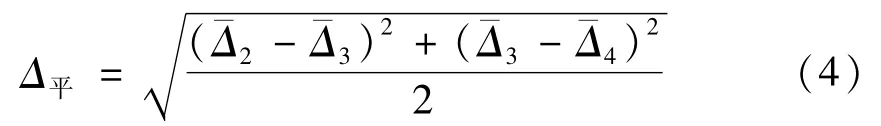
4.2 方差和灵敏系数

依据方差公式

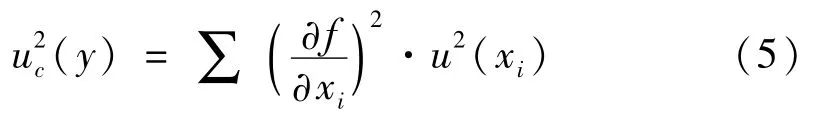
可得

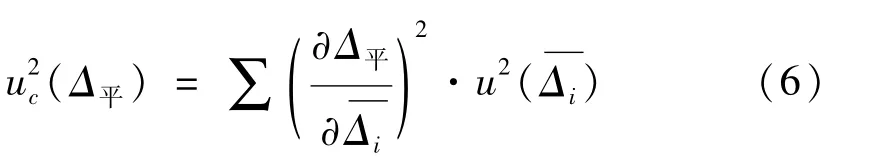
由公式（4）可得

4.3 标准不确定度分量的计算

各直角坐标板上被测激光线的测量读数引入的不确定度分量 u（Δi）

4.3.1 直角坐标板的误差引入的不确定度分量u1（¯Δi）

直角坐标板的刻线间距误差在±0.1 mm以内，作均匀分布处理，则

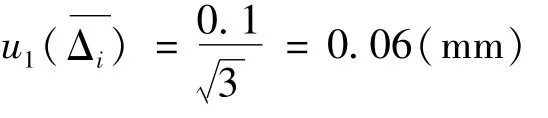
4.3.2 测量重复性引入的不确定度分量u2（¯Δi）

由激光线宽和读数误差等因素引入的不确定度分量均可以采用测量重复性实验进行评定。通过实验重复测量10次，得到其单次测量的实验标准差为0.20 mm。实际测量过程中，采用三次重复读数取平均值，计算其平均值的测量标准差为

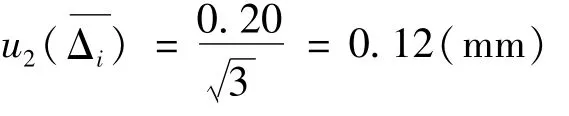
4.3.3 各个直角坐标板之间的水平误差引入的不确定度分量 u3（¯Δi）

1）水准仪误差引入的不确定度分量u31（¯Δi）

测量过程中采用水准仪标定使所有直角坐标板的原点处于同一水平基准面内，其误差可忽略不计。

2）直角坐标板原点的水平误差引入的不确定度分量u32（¯Δi）

测量过程中用水准仪标定使所有直角坐标板的原点处于同一水平基准面内，且直角坐标板的坐标轴与水准仪十字丝重合，因此直角坐标板的水平误差不会超过0.2 mm，估计其呈均匀分布，则

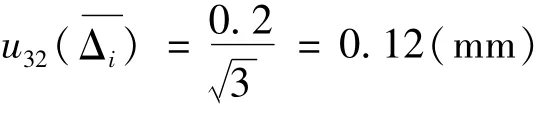
合成以上两项，则

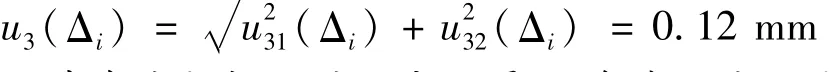
4.3.4 直角坐标板间的距离测量误差引入的不确定度分量u4（¯Δi）

由于各远点直角坐标板与被测仪器间呈45°夹角，因此各相邻直角坐标板间的距离等于远点直角坐标板3与被测仪器的距离，用钢卷尺或全站仪标定其距离时，误差可以控制在10 mm以内，因此由其引入的测量误差为tan（1/1000）×10000≈0.17（mm），估计其呈均匀分布，则

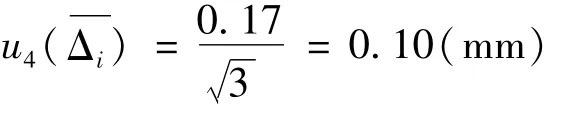
各直角坐标板上被测激光线的测量读数的不确定度分量如表1所示。

表1 各直角坐标板上被测激光线的测量读数的不确定度分量表

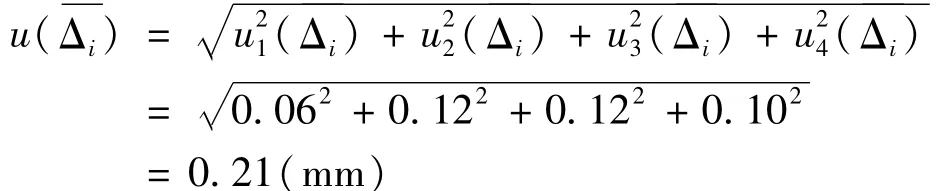
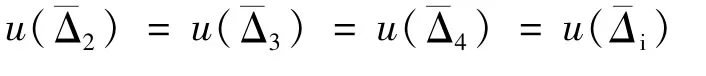
4.4 合成标准不确定度

4.4.1 标准不确定度分量一览表

标准不确定度分量如表2所示。

表2 标准不确定分量一览表

4.4.2 合成标准不确定度

4.5 测量结果的不确定度

取包含因子k=2，则扩展不确定度为

U=kuc（Δ平）=2×0.26 mm≈0.5 mm （k=2）

由于测量结果和被检仪器与远点目标板之间的距离L2有关，因此水平激光线误差测量结果的扩展不确定度可表示为

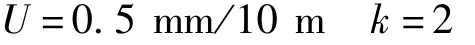
5 结束语

通过对激光标线仪工作原理和误差来源进行分析，提出了一种简捷易行的校准装置设计方案和测量方法，可为生产企业在生产过程中对该产品进行质量与性能评价提供技术借鉴。可根据实验室的具体情况对校准装置进行合理的空间布局设置，例如，利用架设平行光管的方法来节约空间。未来在本文研究的基础上加入光机电一体化设计理念，可利用CCD图像位置探测技术实现测量数据的采集和处理。本文的研究内容将为制定相应的国家计量技术规范提供了技术支撑。