疫情期间社区商超物资配送路径优化研究

刘 娜，张 玺，石超峰

(1.重庆交通大学 交通运输学院，重庆 400074；2.重庆交通大学 经济与管理学院，重庆 400074)

2020年春节伊始，新型冠状病毒疫情首先在武汉出现，随后迅速笼罩到全国。疫情防控当前，确保社区居民生活物资的供应与配送成为政府工作的重中之重。无接触式配送响应疫情态势，各地社区推广生活物资统一购办方式，创新“商超+社区”配送模式确保居民基本生活用品配送，具体的物资配送流程见图1。商超到各个社区的配送路径优化是物资供应保障高效化、及时化的核心环节，是打赢疫情防控攻坚战的关键所在。因此，对社区商超物资配送路径进行优化研究刻不容缓。

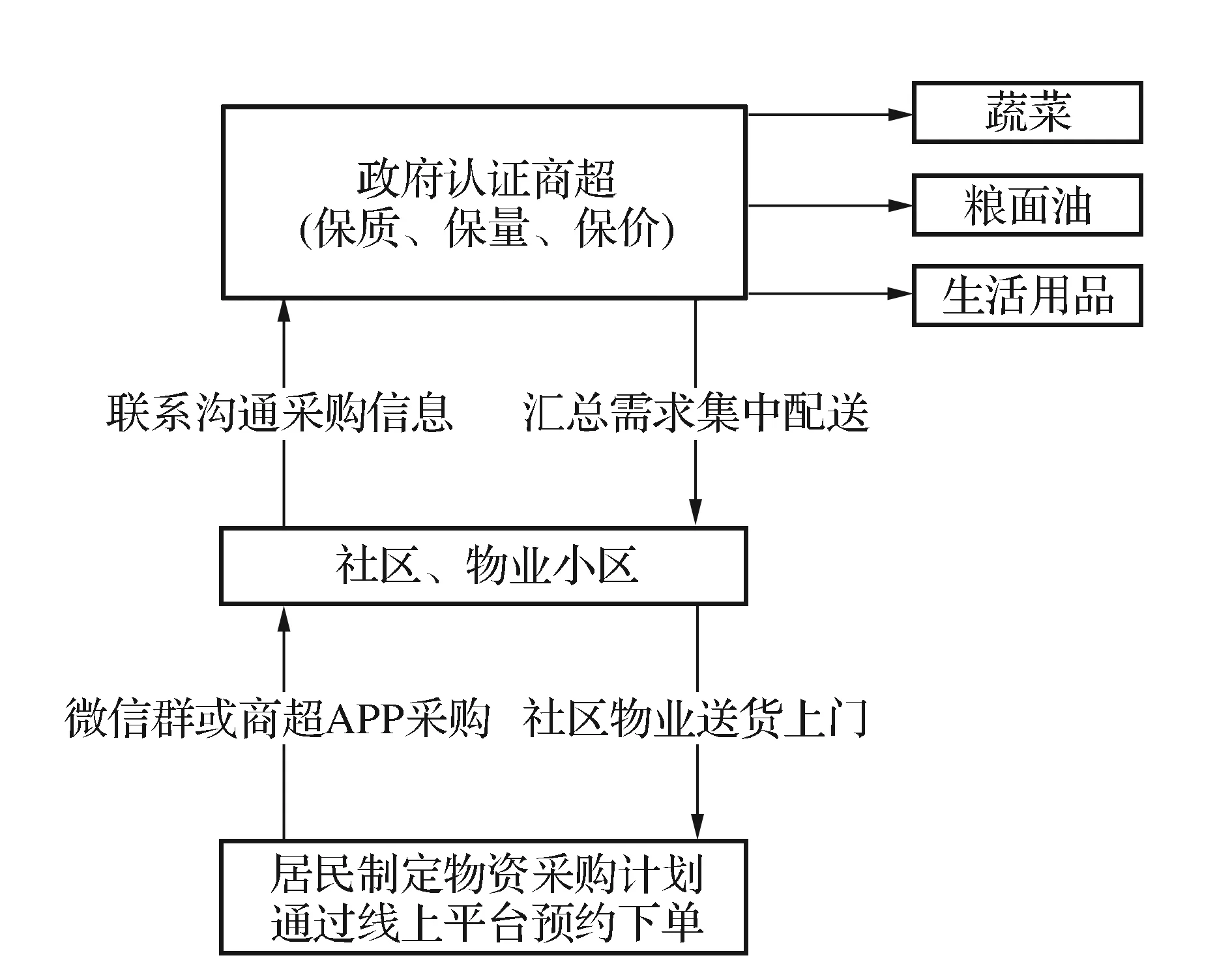
图1 物资配送流程

在快递、大型超市商场物流配送等行业车辆路径规划有广泛的应用前景。文献[1]建立总距离最短的混合整数规划模型，使用Lingo11.0对其求解，得到合理的生活垃圾收运路径。文献[2]考虑配送路径、载重、时间窗限制并以配送费用最低、配送时间最小建立模型，结合遗传算法并运用大数据平台对其求解。文献[3]以总配送时间最低为目标函数，应用Beam-PSO优化算法对模型进行处理。文献[4]研究带有越库策略的生鲜农产品配送问题，提出以总成本为目标的模型。文献[5]提出一种两阶段的禁忌搜索算法,研究开放式的第三方物流家具配送问题。

旅行商问题(Traveling Salesman Problem，TSP)属于车辆路径规划的特例，是经典的组合优化问题。目前，对解算TSP问题方法的研究已成为热点。近年来，启发式算法作为有效求解TSP问题的现代智能算法被普遍使用，较为热门的有遗传算法、蚂蚁算法、离散蝴蝶算法、神经网络等。其中，文献[6]对混合遗传模拟算法做出改进且应用于TSP优化中，该算法对中小规模的算例求解精度较高。文献[7]使用2-opt改进遗传算法中的变异与交叉算子，并应用到某洒水配送实际案例中来减少行程。文献[8]考虑分工合作的思想，结合改进的聚类蚁群算法，提出1种显著减少运行时间的分层递进算法来求解大规模TSP问题。文献[9]针对TSP的松弛问题，通过进行一系列线性整数规划求解，提出有效生成子回路消除约束的方法来极大地提高算法的求解效率。文献[10]为提高算法的搜寻能力，在烟花算法中引入混沌优化思想来解决TSP问题。文献[11]利用贪婪机制，利用模拟退火算法与优化的2-opt算子，设计1种改进离散蝴蝶优化算法。本文将疫情期间社区商超生活物资配送路径问题转化为TSP问题，以湖北省黄石港区为研究对象，将SOM神经网络算法、遗传算法求解的结果进行对比分析，遗传算法优化能力更加突出，使用遗传算法的物资配送路径优化既能减少人员流动，又能使商超在疫情期间快速得到配送方案，提高配送效率，为社区居民提供坚实的物资保障。

1 疫情下社区物资配送路径规划问题

1.1 问题描述

疫情影响下某区域内各社区居民在网上挑选物资下单后，商超汇总需求后分派车辆对不同区段进行物资配送，每个区段均由1辆卡车负责配送，对n个社区逐一配送且每个社区只经过1次，最后卡车返回配送中心，求1条配送行程最短的路径。该问题即TSP问题，可以用1个图(Graph)来描述：V={c1,c2,…,ci,…,cn}，i=1,2,…,n是所有社区的集合；ci表示第i个社区，n为社区数目；E={(r,s):r,s∈V}是所有社区间连接的集合；C={cr,s:r,s∈V}是所有社区之间的距离，即求解只能访问1次图G=(V,E,C)中所有社区并返回原出发社区，使访问行程最短。

1.2 数学模型

模型符号定义如下：

dij：社区i与社区j间的距离；

n：所要配送的社区数目；

V：所有配送的社区集；

U：所有配送的社区集的真子集，U⊂V；

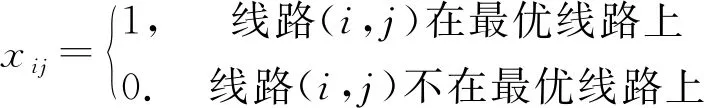
TSP数学模型如下：

(1)

(2)

(3)

(4)

xij∈{0,1}，i,j∈V，i≠j.

(5)

其中，式(1)为以最小化社区配送路径总距离的目标函数；约束(2)(3)表示保证每个社区有且仅有1次被配送；约束(4)表示保证配送路径中不会产生子回路解；约束(5)表示决策变量的取值，如果已经对该社区配送，则xij=1；如果未对该社区配送，则xij=0。

2 求解算法

2.1 SOM算法

自组织映射网络(Self-Organizing Maps，SOM)[12]是1981年由芬兰专家Kohonen提出。它具有自组织、自适应功能，类似于人脑特性，可自动学习到样本的基本属性与内部规则，改变网络结构。目标是将高维空间里的所有点用低维空间中的点来表示，尽量维持点间距离与拓扑关系。

SOM为层次型结构。典型结构是输入层加输出层。其中，输入层通过接受外围信息获得输入模式，传给输出层；输出层从输入模式的分析比较中总结获得规律并分类。TSP问题属于典型的NP难问题[13]，无法应对线性的复杂度问题，SOM网络寻优能力强，无需监督可自动学习到样本数据的输入模式，最终得到1条优化后的最短路径。

SOM算法解决TSP问题的具体步骤如下[14]：

1)神经元位置随机初始化，分布于城市坐标四周。

2)随机挑选1座城市，找到获胜神经元，即距离该城市最近的神经元。采用欧式距离作为距离度量。

3)周围的神经元按高斯分布向获胜神经元移动。具体调整规则如式(6)所示。

Wt+1=Wt+α(t)g(t,N)d(c,Wt).

(6)

式中：Wt+1为当前的神经元；Wt为先前迭代的神经元值；α(t)为学习率；g(t,N)为获胜神经元的邻域函数；d(c,Wt)为神经元与获胜神经元间的距离。

4)若学习率达到设定阈值或迭代次数，则继续步骤5)，否则再重新执行步骤2)。

5)以神经元顺序输出最短配送路径及长度。

2.2 遗传算法

遗传算法(Genetic Algorithm，GA)[15]是把问题模拟为1个生物进化过程来随机搜寻最优解的方法，充分展现了自然界优胜劣汰、适者生存的规律。1975年由美国教授J.Holland首先提出[16]。由于GA算法有很多优良的特性，干扰因素少，直接对个体进行操作，对解决TSP问题有很大的优势。

遗传算法求解TSP问题的具体步骤如下[17]：

1)编码并进行种群初始化。这里采用整数编码的方法。

2)选择适应度函数。适应度值直接反映对应回路的优劣，适应度值定义为目标函数值的倒数，即

(7)

目标函数值越小，适应度值越大，对应产生的回路解越好。

3)计算个体的适应度值，进行选择操作。从旧群体中挑选个体到新群体，被选中的概率与个体的适应度值成正比，取值越大，选中的概率就越大。

4)交叉、变异操作。操作的父代交叉算子选用部分映射交叉，随机选择两个个体完成交叉操作；变异算子选用交换变异算子，随机选择两个变异点并对换位置。

5)进化逆转操作。这里的逆转操作是单方向性的。逆转后认可适应度值有提高的个体，不然无效。

6)判断是否完成进化次数，若未达到要求则执行操作3)，否则继续下一步。

7)输出路径图。根据以上步骤取得结果并输出最短配送路径轨迹。

3 案例比较与分析

3.1 案例说明

本文以疫情期间湖北省黄石港区为实例对该区商超物资配送路径优化问题进行研究。该区共有32个社区需要提供生活物资供给服务，商超考虑到配送效率与各社区的配送距离有关，要合理地规划物资配送车辆路径。根据位置地图得到各个社区位置坐标如表1所示。

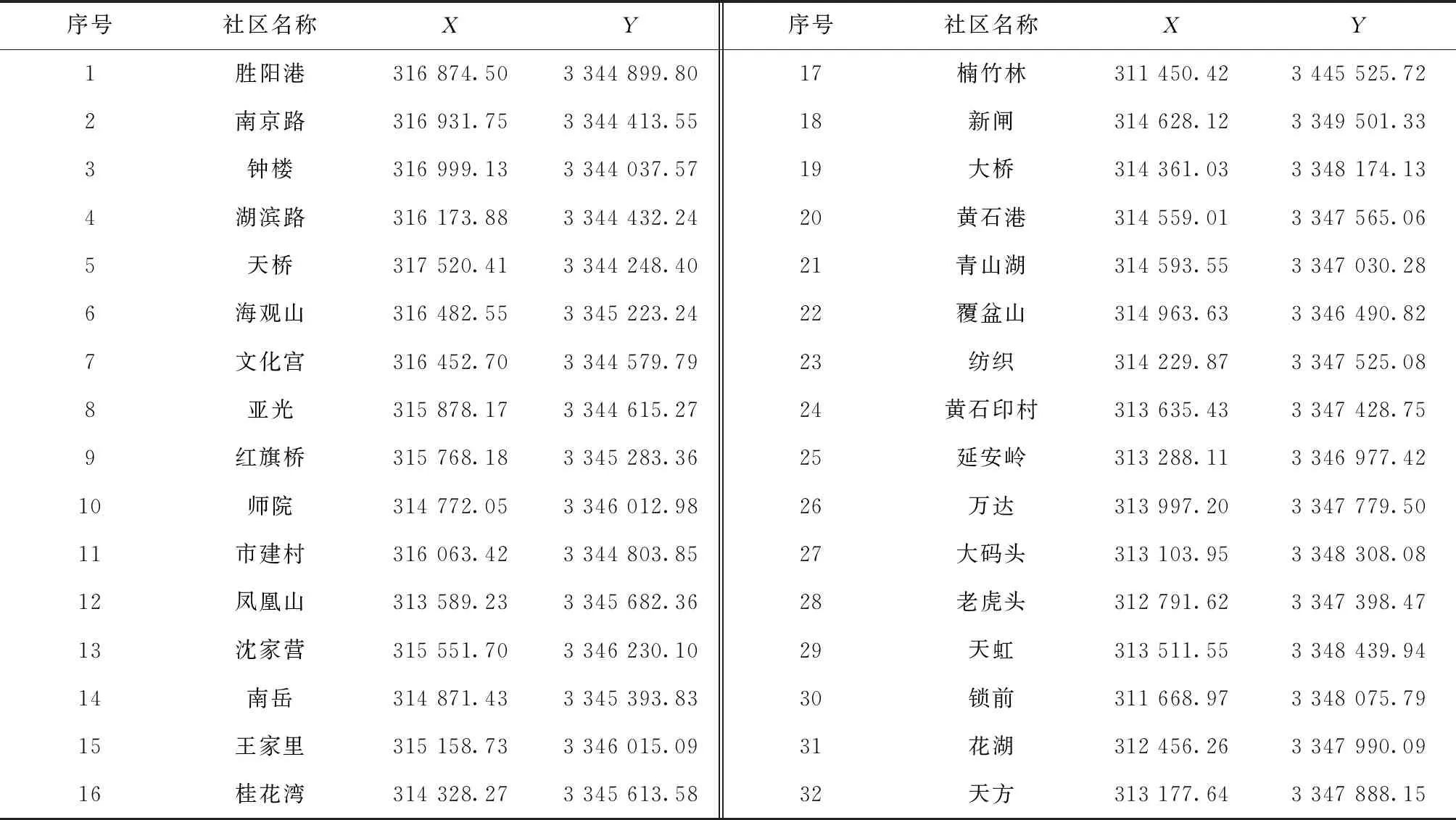
表1 社区位置坐标

3.2 算法比较

本文采用MATLABR2016b编程，分别对SOM和GA两种求解算法进行实现。不同算法下，将程序独立重复运行30次，求出该区商超物资配送路径优化解，并对算法结果比较分析。为保证算法的有效性及准确性，经过多次参数实验测试，在SOM算法中，设定学习率为0.8，学习率衰减率为0.999 97，领域值衰减率为0.999 7，最大迭代次数为10 000；在GA算法中，设定N=100，Pc=0.9，Pm=0.06，MAXGEN=200。通过运行算法记录得到的两种算法平均数据对比如表2所示。

首先，从表2分析得知，GA算法的平均运行时间相对较小，同时得到的平均路径距离也相对较短；两种算法的优化迭代次数相差巨大，GA算法迭代仅160次左右就可搜索到距离为23.5 km的最优路径，而SOM算法要迭代8 000次即GA算法迭代次数的50倍才可搜索出最优配送路径。明显看出，GA算法的收敛速度快，搜寻最优路径的能力较

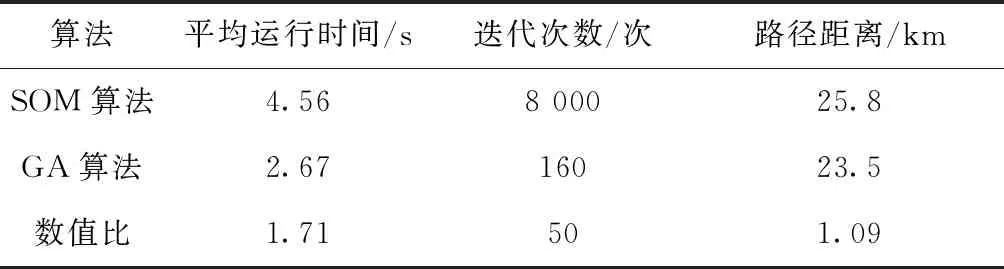
表2 2种算法运行结果比较

强，拥有更高的收敛性能及寻优精度。其次，在实验过程中发现，SOM算法收敛性密切依赖于求解问题的拓扑分布，当分布无规律时很难得到理想结果，GA算法则与其无关，在可接受时间内一定能寻到一个优化路径，虽然非最优，但基本可满足需求。综上分析，GA算法对路径配送优化问题求解的性能更优，效果更佳。

3.3 结果分析

在疫情攻坚战中，综合考虑求解精度与收敛速度，为保障居民生活物资生命线，及时生成配送路径，应用GA算法对该区物资配送方案进行详细地分析。由最近邻点算法得到初始配送路径距离为63.2 km，初始配送路线见表3，初始路径见图2。通过GA算法优化后的路径距离为23.5 km，比初始路径减少39.7 km，优化后的路径距离为初始路径距离的37.2%。可见，GA算法优化后配送距离极大降低，配送成本明显减少。最终优化后的配送路线见表4，轨迹图及进化过程分别见图3、图4。

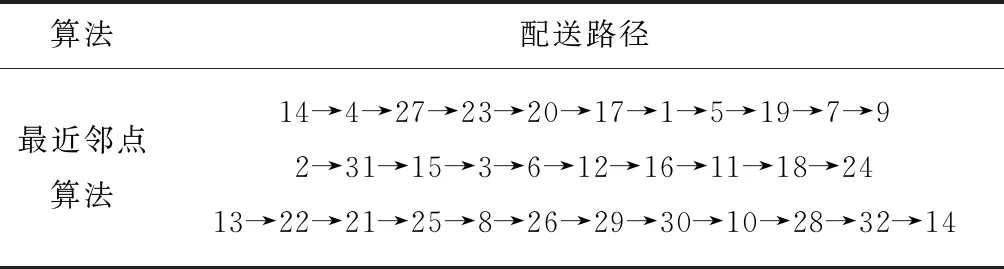
表3 初始配送路线

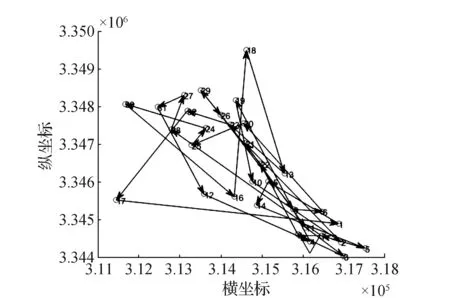
图2 初始路线

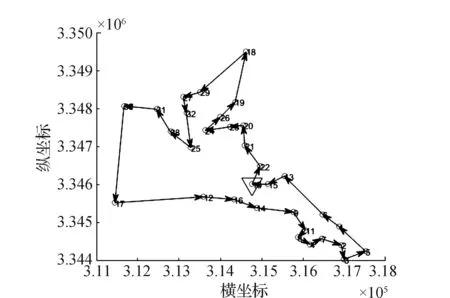
图3 优化后的轨迹

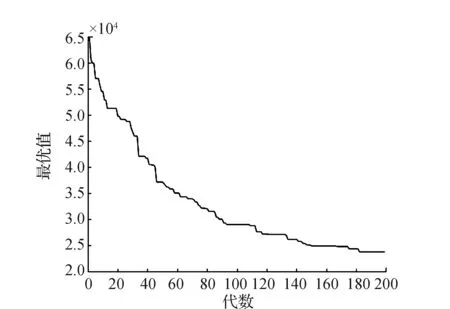
图4 进化过程

同时，针对GA算法中参数种群规模N及最大迭代次数MAXGEN的变化进一步验证分析。对不同取值的N和MAXGEN重复做20次运算，计算平均最优值。不同N与MAXGEN取值下平均最优解见图5、图6。

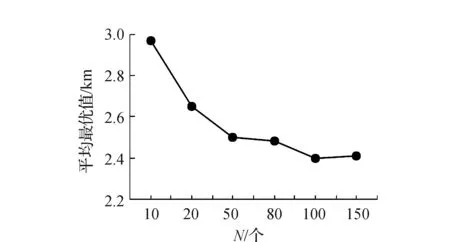
图5 不同N下平均最优值的变化

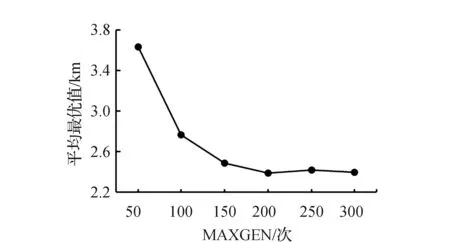
图6 不同MAXGEN下平均最优值的变化

观察图5、图6可知，随着种群规模与迭代次数的增加，平均最优值减小，解的平均最优性增大，算法收敛到最优解的概率会增大。由于算法具有随机性，平均最优值的变化并不是单调的，会出现相邻规模反复的现象。在实验过程中发现参数值的设置与最终求解结果联系紧密，参数设置的不合理可能会导致所求的解不一定是最优解，增加种群数目及迭代次数有利于最优解的获得，商超可减少物资配送时间，提高物资供给效率。

4 结束语

本文在考虑新型冠状病毒肺炎疫情影响下，对社区商超物资配送路径优化问题进行了研究。运用SOM和GA两种算法到湖北省黄石港区社区物资配送案例中，由案例结果比较发现：GA算法拥有更高的求解精度及收敛速度，优化后的路径距离为初始路径距离的37.2%，能够迅速而精确地获得最优配送方案。而后又展开分析种群规模、迭代次数等重要参数对配送方案的影响，优化后的结果可显著加快商超配送速度，节约配送成本，及时快速地完成社区配送任务，纾解因疫情为居民生活带来的众多不便，保障社区居民基本生活需求，推动疫情态势不断朝着好的方向发展。未来可考虑社区对物资配送车辆有时间条件要求的前提下，引入时间窗的限制，研究含有时间约束的社区商超物资配送路径优化问题，使得居民需求得到进一步的满足。