基于累积前景理论的通勤者出行方式选择

2020-09-18姚兰

交通科技与经济 2020年5期

姚兰

(兰州交通大学交通运输学院,甘肃兰州 730070)

随着城镇化进程的加快，城市居民的出行问题已成为备受关注的话题，对于个体出行行为的研究，已成为城市交通规划、建设和管理工作中不可或缺的部分[1-3]。通勤者作为出行中的主力军，在不确定条件下对于出行方式的选择受到了自己性格、风险偏好、环境等因素的影响，基于有限理性的假设研究通勤者出行方式的选择行为，可有效缓解城市交通拥堵，提高通勤者出行效率[4-5]。

目前，许多学者就出行方式选择问题进行了研究。以累积前景理论为基础，张薇等[6]以公交、出租车和私家车3种出行方式为例，研究了居民出行方式的选择问题，分析了不同参照点下各交通方式前景值的变化情况；田丽君等[7]以地铁、自驾车和地铁与自驾车换乘3种交通方式为例，对比分析了期望效用理论和累积前景理论下通勤者对于交通方式选择的差异性；徐爱庆等[8]设置了动态出行参考点，考虑了航班容量限制因素，认为累积前景理论能够有效描述机场群旅客出行决策行为；李小静等[9]从价值和可靠度2个方面，研究了通勤者在不确定条件下的出行路径选择；龙雪琴等[10]考虑了不同出行者对收益和损失的敏感性，分析了突发事件下出行者路径选择的行为规律。诸葛承祥等[11]以通勤者出行时间与出行方式选择特征为基础，建立出行时间—出行方式、出行方式—出行时间两个方向的 Nested Logit 模型，杨艳妮等[12]依据北京市出行大数据，探讨了出行者在公共交通中的选择特性，得出了不同群体对部分变量的敏感性。

本文以城市公共系统中最普遍的出行方式为研究对象，考虑通勤者的有限理性，以出行者在出行过程中主要关心的行程时间和出行费用为参考点，建立基于累积前景理论的出行方式选择模型，更加符合通勤者在出行方式选择中的实际情况。

1 问题描述

在大中型城市中，通勤者在高峰期对于出行方式面临多种选择，主要包括地铁、公交和出租车(作为城市公共交通系统中最普遍的3种交通方式)，出行时间和出行费用是影响通勤者出行方式选择的主要因素。根据累积前景理论的心理学分析，通勤者在出行前通常会预先假定一个参照点，该参照点是对通勤者本次出行心理预期的反映，并由参照点来评估选择某种交通方式后的收益或损失[13]。现实中，人们的心理更加看重的是收益或损失的相对值而不是绝对值。因此，通勤者在出行前首先会对这两个因素引起的出行成本进行评估，再对照出行参照点选取累积前景值最大的交通方式出行。通勤者的出行决策过程如图1所示。

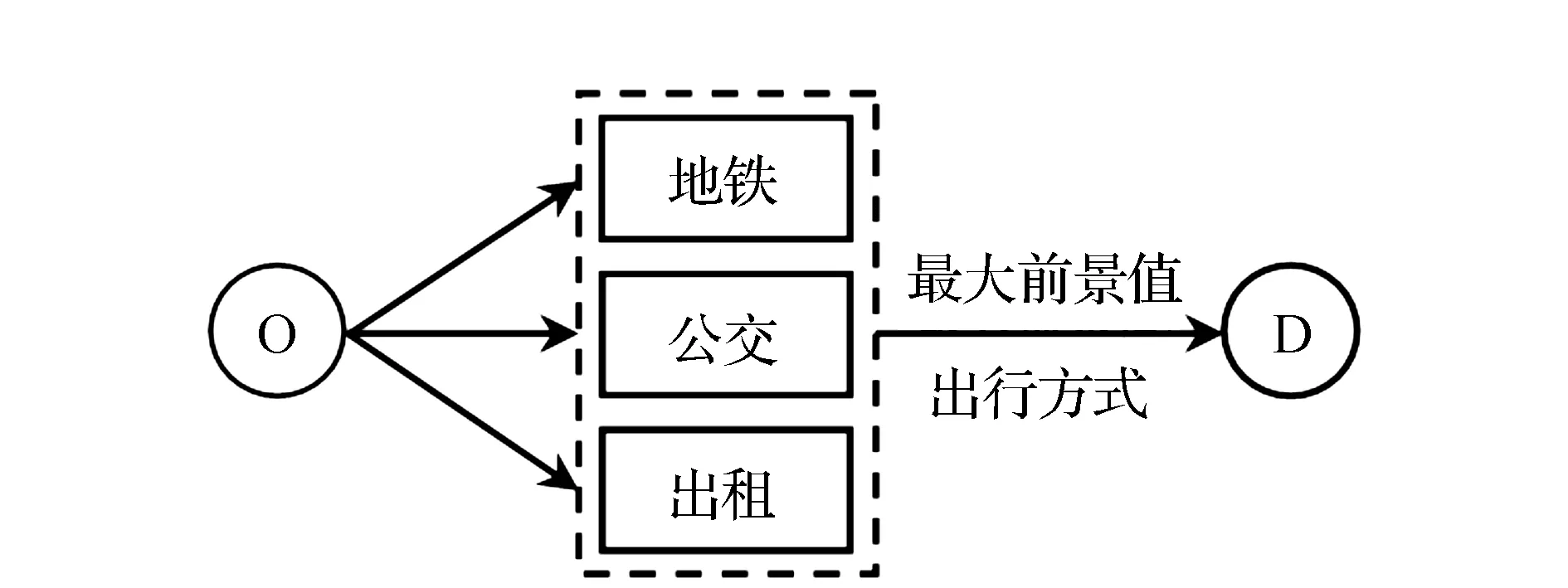
图1 通勤者出行决策过程

本文将行程时间和行程费用作为通勤者出行方式选择的参照点，其中行程时间指通勤者在出行过程中所花费的全部时间，包括行驶时间、停车时间和等车时间等；出行费用指通勤者在出行过程中所负担的全部经济成本，主要体现在票价方面。为便于模型说明，将实际问题描述如下：

1)出行方式方案集合：A={A1,A2,…，Ai}，其中Ai代表第i种出行方式，i=3。

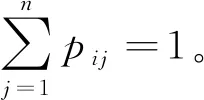
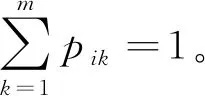
6)参考点集合：K={K1,K2}，其中K1表示行程时间参考点，即通勤者对行程时间指标的预期值，K2表示出行费用参考点，即通勤者对出行费用指标的预期值，本文参照点的取值是依据基于行程时间和出行费用估计的出行效用变化量。

7)指标权重集合：W={w1,w2}，其中w1表示行程时间指标权重，w2表示行程费用指标权重，并且w1+w2=1。

2 模型构建

2.1 行程时间参考点

行程时间参照点是通勤者对某次出行所需时间的心理期望值，根据人们的出行习惯，通勤者一般会根据自己的不同要求以及出行经验等假定出自己的参照点K1，当通勤者按照某种出行方式出行后可能会出现若干种行程时间情景，此时情景Sj的行程时间对行程时间参照点K1的差值为

Δxit=K1-Tj.

(1)

当Δx≤0时，表示情景Sj的行程时间大于通勤者心理期望值，通勤者心理感知为损失；当Δx≥0时，表示情景Sj的行程时间小于通勤者心理期望值，通勤者心理感知为收益。

1)价值函数。根据Tversky和Kahneman[12]提出的价值函数形式，定义情景Sj对行程时间的价值为

(2)

其中，α和β(0≤α，β≤1)为风险敏感系数，表示行程时间的收益和损失价值函数的凹凸程度，价值函数曲线如图2所示。

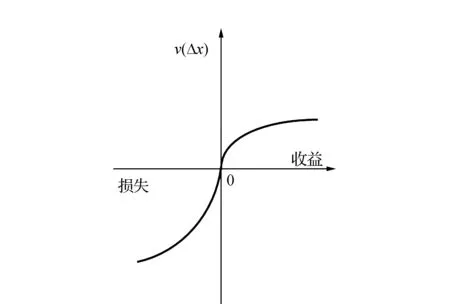
图2 价值函数

α和β越大，则收益和损失价值函数的凹凸程度越大，价值函数曲线体现了通勤者对行程时间敏感性递减的心理行为特征；λ为损失规避系数，λ≥1时体现了出行者对损失更加敏感的心理行为特征，并且λ越大损失规避程度越大。研究表明，当取值α=0.89，β=0.92，λ=2.25时最符合决策者心理特征[14]。

2)权重函数。本文采用由Kahneman和Tversky提出的权重函数，如图3所示。

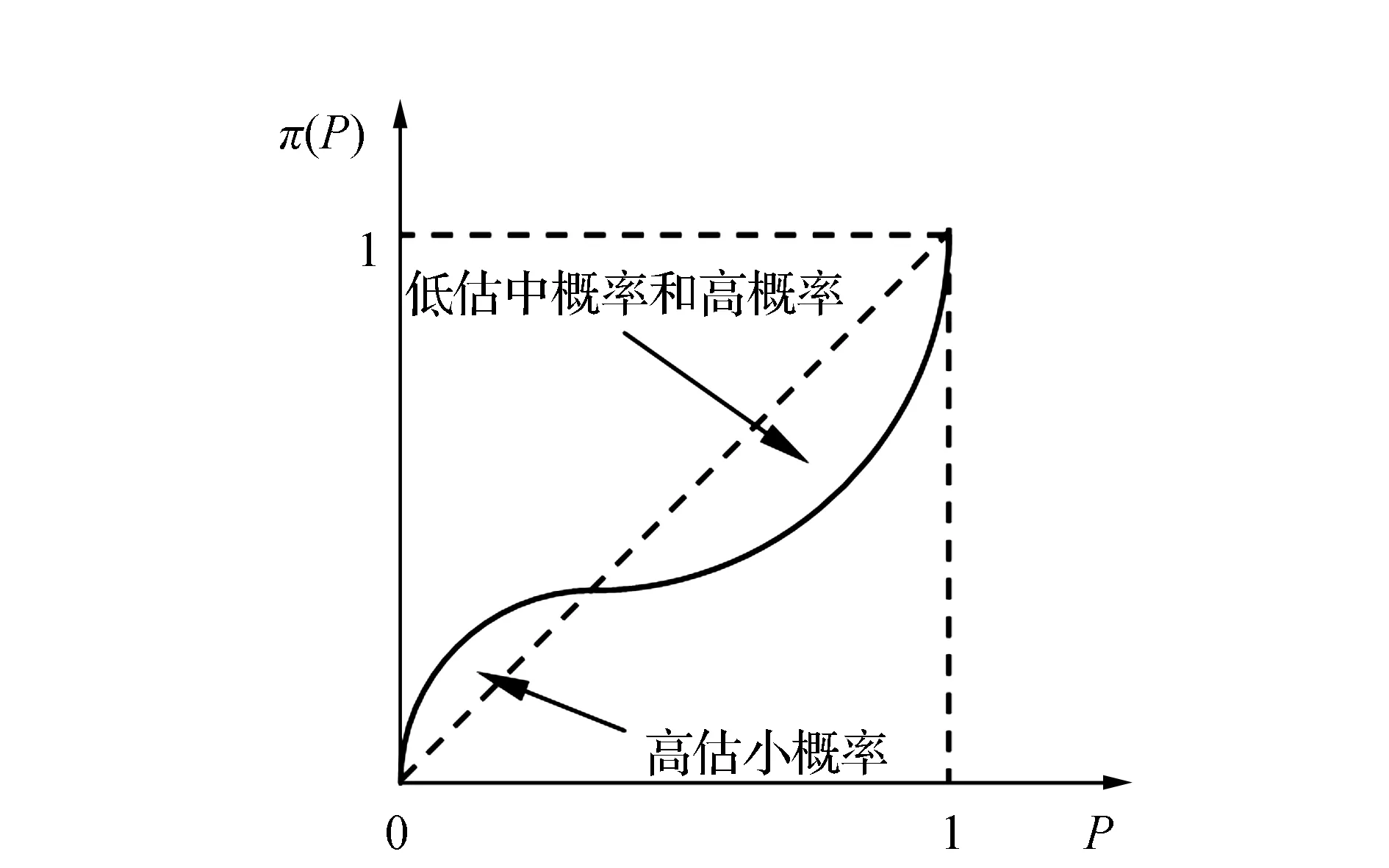
图3 权重决策函数

在收益情况下，概率权重函数为

(3)

在损失情况下，概率权重函数为

(4)

其中，γ和δ为个体行为偏好系数，根据实验数据结论[15]，一般标定γ=0.61，δ=0.69。由权重函数图可看出，人们经常会表现出高估低概率事件、低估中概率和高概率事件。

3)累积前景值。综上所述，出行方式Ai的行程时间累积前景值可表示为

(5)

2.2 出行费用参考点

与行程时间相比，如果通勤者选择了某种交通方式，出行费用便随之确定。但不同通勤者的自身条件及需求不同，因此，会假定不同的行程费用参考点从而选择相应的交通方式。出行方式Ai的累积前景值具体计算如下：

1)价值函数

Δxic=K2-Tk.

(6)

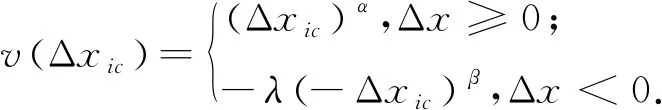
(7)

2)权重函数

(8)

(9)

3)累积前景值

(10)

2.3 综合累积前景值

综合之前所述内容，综合考虑行程时间与出行费用2个参考点，则出行方式Ai的综合累积前景值为

(11)

其中，指标权重w1与w2的取值可通过调查统计或专家打分方法得到。由于行程时间累积前景值与行程费用累积前景值的量纲不同，会对计算结果产生一定影响，因此，对方案Ai的行程时间累积前景值CPVit与出行费用累积前景值CPVic进行规范化[6]，可得

(12)

(13)

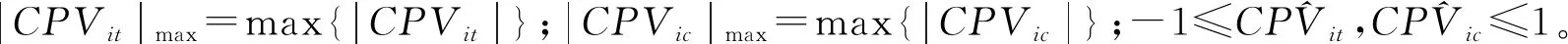
显然，综合累积前景值越大说明该出行方式越符合通勤者心理，最大综合前景值所对应的出行方式即为通勤者的首选方案。

3 案例分析

对于中等出行距离，假设通勤者的某次出行有以下3种交通方式可供选择：

1)方式A1。地铁，19 min到达，票价为4 元。

2)方式A2。公交车，30 min到达概率为70%，45 min到达概率为30%，票价为2元。

3)方式A3。出租车，14 min到达概率为80%，24 min到达概率为20%，票价为 16元。

在本案例中，行程时间情景状态集合为St={14,19,24,30,45}；出行费用情景状态集合为Sc={2,4,16}；行程时间参照点K1分别取15,20,25,30,35,40,45,50；出行费用参照点K2分别取2,4,6,8,10,12,14,16，该案例中参照点是根据通勤者已有的出行经验，并结合实际情况来确定。

3.1 行程时间累积前景值分析

不考虑出行费用，只将行程时间作为参考点，根据累积前景理论计算得出不同参照点下各出行方式的累积前景值，利用最小二乘法原理，通过拟合软件对行程时间与累积前景值进行非线性拟合，拟合结果如图4所示。

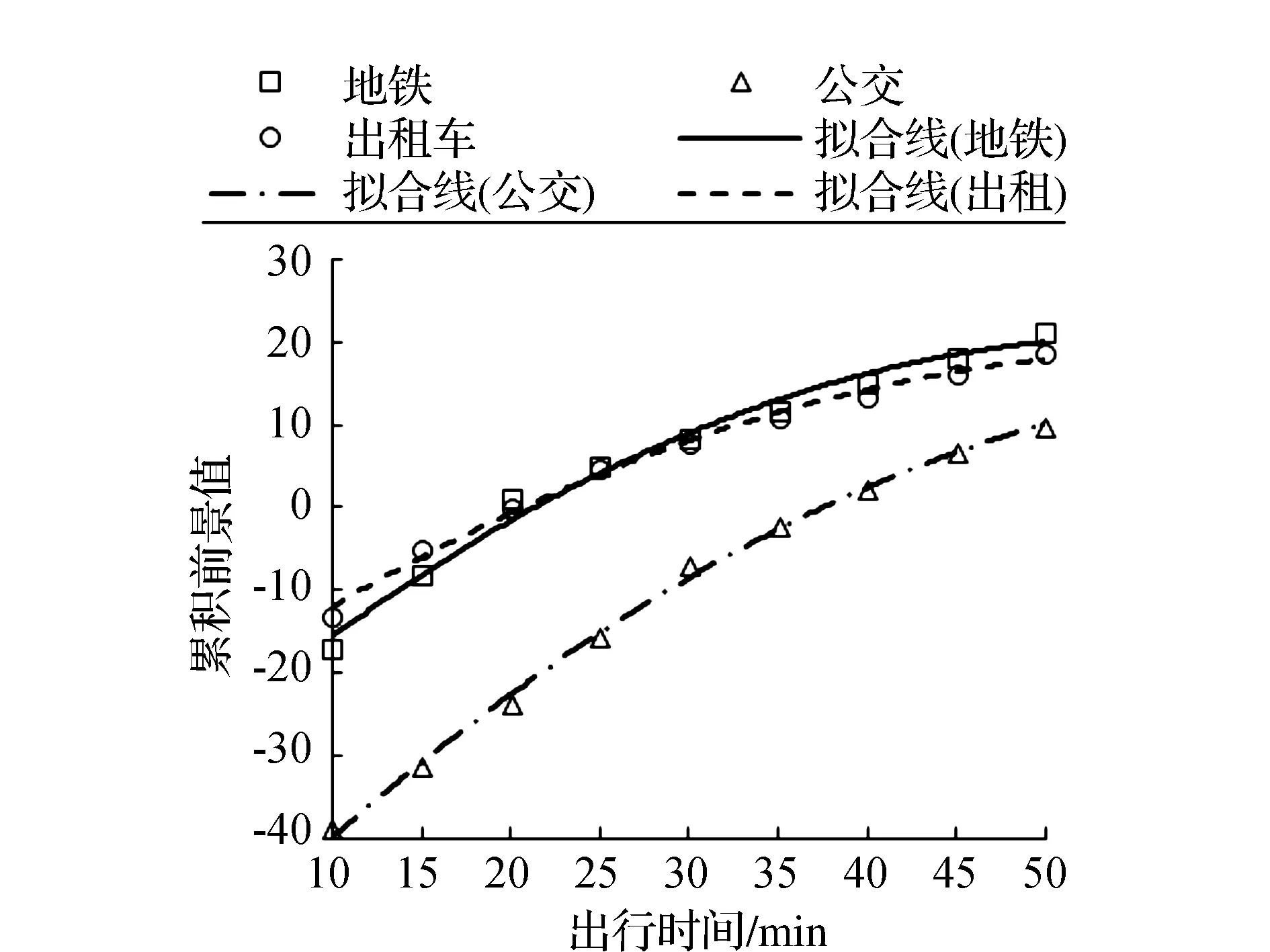
图4 各出行方式行程时间累积前景值拟合曲线

其中，地铁的累积前景值拟合曲线方程为y1=-0.016 9x2+1.904 8x-32.9，拟合度为R2=0.988 7；公交车的拟合曲线方程为y2=-0.016x2+2.208x-60.324，拟合度为R2=0.997 8；出租车的拟合曲线方程为y3=-0.012 7x2+1.506 6x-25.709，拟合度为R2=0.993 8。

从图4可以看出，随着时间参照点取值的依次增大，3种交通方式的前景值均呈现出上升趋势。地铁和出租车的前景值较接近，且均高于公交车，行程时间参照点在10～20 min之间，出租车的前景值略高于地铁，但当参照点大于30 min时，地铁的前景值又高于出租车，且从图中明显可知，当参照点在20～30 min时，两种交通方式的累积前景值存在交点。由两种出行方式的拟合曲线联立可解得交点为x=24.27，y=3.37，即当行程时间参考点为24.27 min时，两种出行方式的累积前景值相等，通勤者出行时选择地铁和出租车的概率接近，通勤者可根据自己的出行偏好选择合适的交通工具。因此，当通勤者对行程时间有较高要求，而对出行费用不作要求时，可选择将出租车作为自己的通勤工具。

3.2 出行费用累积前景值分析

同理，不考虑行程时间，只将出行费用作为参考点，根据累积前景理论计算可得不同参照点下各出行方式的累积前景值，利用最小二乘法原理，通过拟合软件对出行费用与累积前景值进行非线性拟合，拟合结果如图5所示。

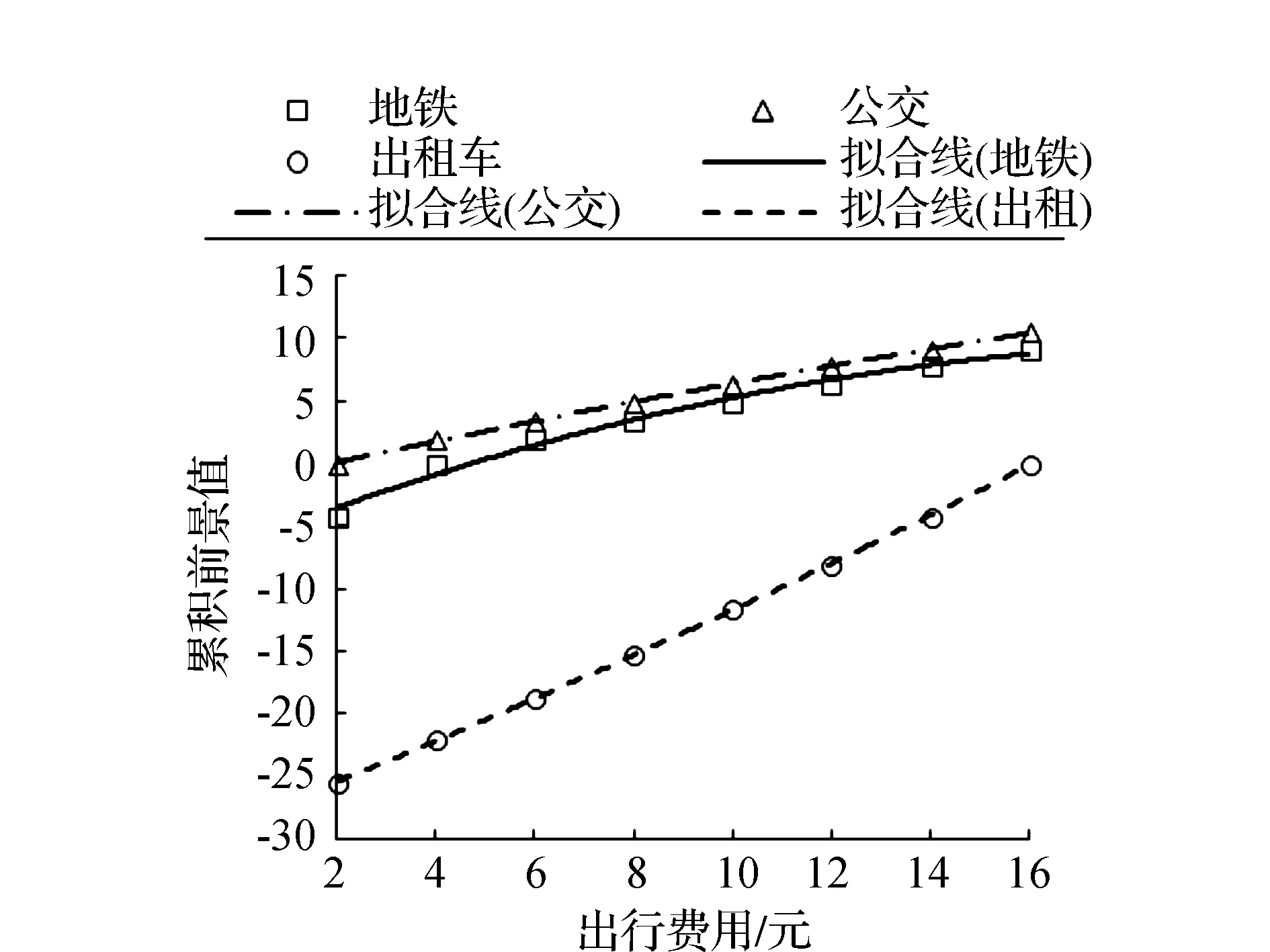
图5 各出行方式行程费用累积前景值拟合曲线

其中，地铁的累积前景值拟合曲线方程为y1=-0.036 6x2+1.536 8x-6.447 8，拟合度为R2=0.986 1；公交的拟合曲线方程为y2=-0.008 6x2+0.892 9x-1.669 8，拟合度为R2=0.999 7；出租车的拟合曲线方程为y3=0.015x2+1.536 1x-28.556，拟合度为R2=0.999 9。

由于公交票价和地铁票价差距较小，而出租车出行费用远远高于公交和地铁的出行费用，因此，公交和地铁的累积前景值远远大于出租车的累积前景值。从3种出行方式的拟合曲线图可知，在不同出行费用参考点下，公交和地铁的累积前景值较接近，由于公交的票价小于地铁票价，因此，地铁的累积前景值虽与公交接近，但始终小于公交的前景值，通勤者在不考虑行程时间的情况下，采用公交出行可降低出行费用。从拟合曲线的斜率来看，公交和地铁的曲线斜率较小，而出租车的曲线斜率较大，说明出租车的累积前景值随参照点的增加增长幅度较大，越来越接近人们的心理预期。

3.3 综合累积前景值分析

对于通勤者来说，单纯考虑行程时间或出行费用的情况较少，大多数情况下，对出行方式的选择是基于行程时间和出行费用二者共同作用的结果。相比出行费用，通勤者更关心的是行程时间，根据调查数据，这里取指标权重w1=0.7，w2=0.3。基于累积前景理论，各出行方式在行程时间和出行费用共同影响下的综合累积前景值三维曲面图如图6所示。

图6 各出行方式综合累积前景值三维曲面

从三维曲面图可以看出，在3种交通方式中，地铁的累积前景值始终高于出租车和公交的累积前景值，这也符合大多数城市通勤者的出行现象。随着出行费用和行程时间的不断增大，3种出行方式的累积前景值变化一致，均呈增长趋势。公交和出租的曲面图相对平滑，而在地铁的曲面图中，有一处凸起段，根据计算数据分析可知，当出行费用参照点为10元、行程时间参照点在15～35 min时，地铁的累积前景值相比相邻区段较大，说明在该区段内选择地铁出行方式距通勤者的预期值较接近。

为了更加清晰的看到各交通方式综合累积前景值的具体变化情况，将出行费用参照点分别为2、4、16时的截面图单独截出，如图7～图9所示。

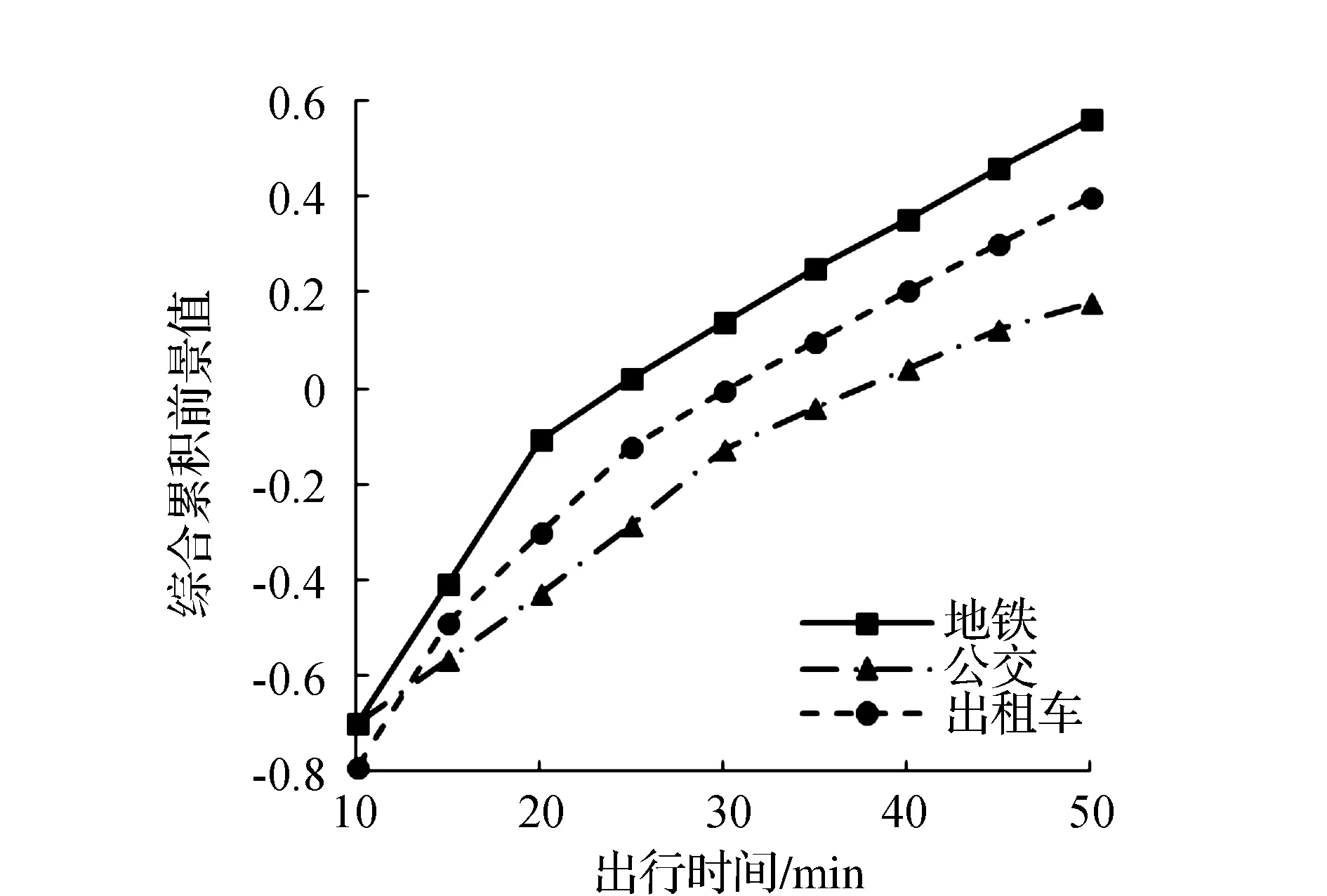
图7 K2=2时各出行方式综合累积前景值对比

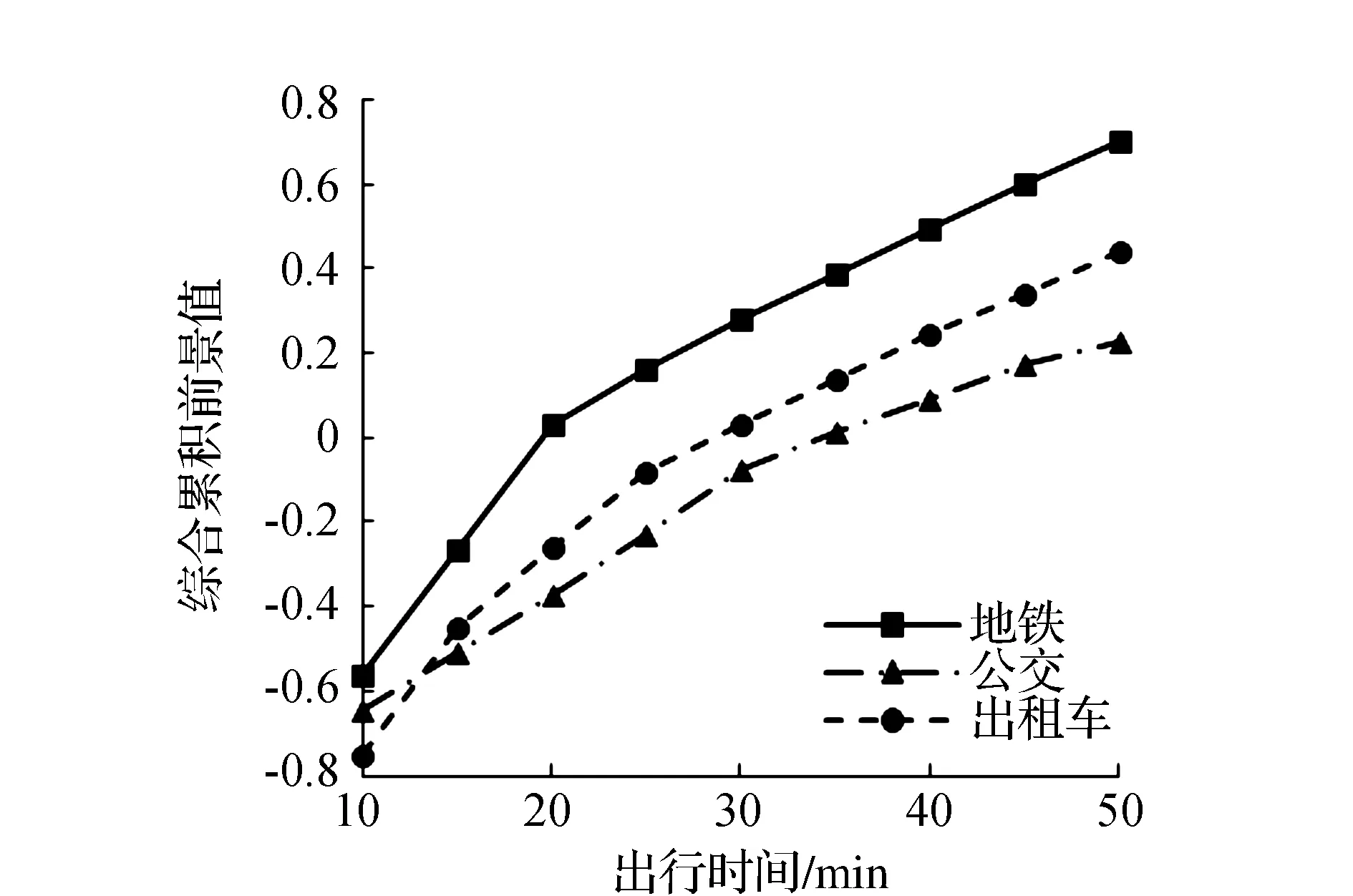
图8 K2=4时各出行方式综合累积前景值对比

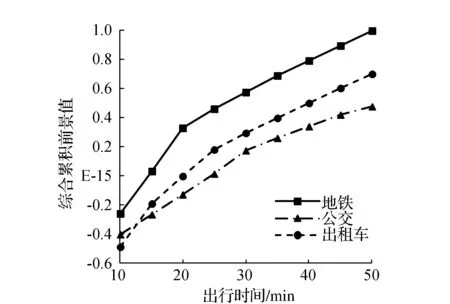
图9 K2=16时各出行方式综合累积前景值对比

公交车票价较低但所需时间较长，而出租车票价较高但行程时间较短，这两种交通方式各有自己的优缺点，从图7可以看出，不论当出行费用参考点取值如何变化，二者的综合累积前景值的差值基本保持一定。地铁所需行程时间较出租车稍长，票价较公交车稍高，由图可知，无论当出行费用参考点取何值，地铁的综合累积前景值始终高于另外两种交通方式，且随着出行费用参照点的增大，其综合累积前景值与其他两种交通方式的综合累积前景值差值逐渐变大。

对比分析图7～图9，当出行费用不同时，3种出行方式的综合累积前景值各自变化趋势相同，近似呈现分段折线变化，其中，地铁的转折点为20 min、公交的转折点为30 min和45 min，出租车的转折点为15 min和25 min，各分段折线的斜率计算如表1所示。

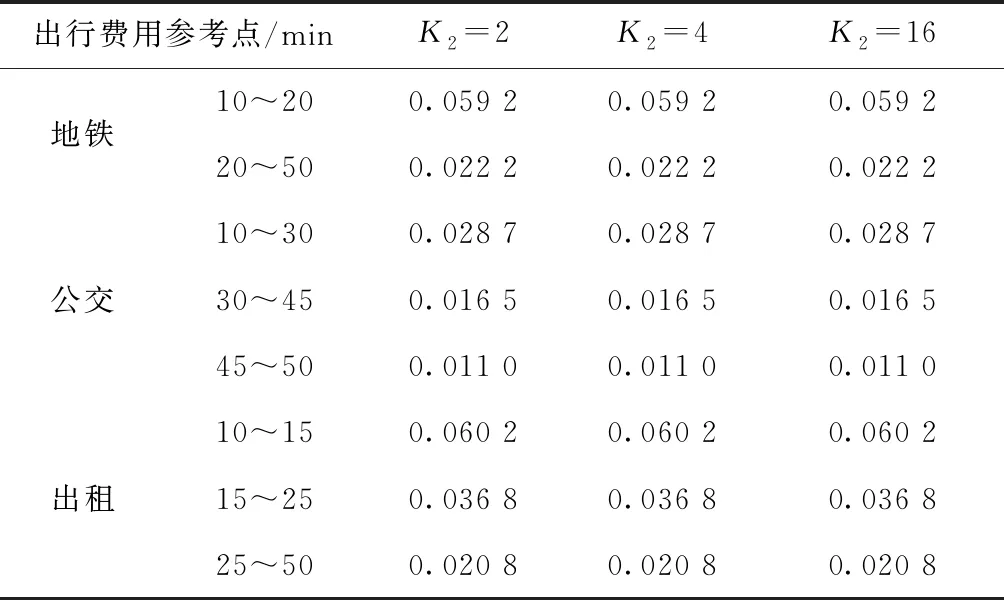
表1 各出行方式分段折线斜率计算

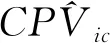
从各出行方式分段折线斜率对比来看，3种出行方式转折点前的斜率均大于转折点后的斜率，即转折点前的行程时间参考点相比转折点后对综合累积前景值的影响较大，这也说明了行程时间对通勤者在出行方式选择中的影响较大。

综上所述，在考虑行程时间和出行费用的情况下，通勤者往往会选择时间较快、费用较低、准时性较高的出行方式，参考点的变化对于出行方式的选择有较大的影响，不同行程时间和不同出行费用期望值下会有不同的出行方式选择。通过对比3种出行方式，随着行程时间和出行费用的变化，地铁的累积前景值始终高于出租和公交，即通勤者对于地铁出行的选择要高于其余两种交通。