基于混合蛙跳算法优化SVM的个人信用风险评估

王 妍，陆云峰

(江苏商贸职业学院，江苏 南通 226011)

1 支持向量机

支持向量机(SVM)可分为线性支持向量机和非线性支持向量机。对于非线性问题，可以通过定义一种映射来把原空间中的非线性问题转化为新空间中的(C,g)线性问题，然后求解最优分类面，这个新空间通常是高维的。从理论上来说，用这种转化可以把相对比较复杂的问题用简单的线性判别函数来解决。但转化后新空间的维度通常比较高，经常会出现“维数灾难”的问题，为问题处理带来了新的困难，因此SVM需要一种能够避免在高维空间中直接求解的方法[1]。

如今，大部分建立的SVM模型中都采用了RBF核函数，因为其参数较少且分类正确率高而成为了首选的核函数。本研究建立SVM模型所采用的核函数也是RBF核函数，RBF的径向作用范围是被其宽度参数g所控制的。惩罚参数C是用来调节SVM建立的最优分类超平面对样本进行分类时的间隔大小与分类准确度之间的妥协偏好权重。对此，选取适合的 RBF核函数参数g和SVM惩罚参数C就变成了目前需要解决的关键性问题[2]。

2 利用混合蛙跳算法进行SVM超参数优化

混合蛙跳算法进行超参数寻优的具体过程：步骤1：青蛙种群初始化，设置青蛙个数、子蛙群数目、混合迭代次数和子蛙群中局部迭代次数。步骤2：计算每一个青蛙个体的适应度值，运用3折交叉验证(3-CV)方法计算出每一个个体的平均分类准确率(CVA)即为适应度值，CVA越高，适应度值越高。步骤3：把所有青蛙个体按适应度大小从优到劣排序，按一定规则把青蛙个体分配到各个子蛙群中。步骤4：运用更新策略对子蛙群中适应度最差的个体进行更新，以得到一个较好的解。步骤5：对子蛙群中的个体再按适应度大小进行排序，并转到步骤4，重复这一操作，直至达到事先设定的局部迭代次数。步骤6：当所有子蛙群都完成了局部搜索后，若满足混合迭代次数，则算法结束，输出最优目标值和最优超参数组(C,g)，否则返回步骤2。

3 指标与数据说明

本研究数据来源于第五届“泰迪杯”数据挖掘挑战赛。该数据为某银行的个人信贷数据，包含了1 000条样本数据，每条样本数据有16个特征，前15个特征是有关贷款人的各种信用特征，如银行账户状态、个人居住情况、年龄等。最后一个特征是贷款人的违约情况，主要分为两类，0为正常，1为违约。

选取年龄、信用历史、婚姻关系、是否为外籍人士、个人居住情况、在这家银行现有的信贷数量等15个信用评估特征作为输入变量。其中，银行账户状态的持续月份、信用保证金、年龄为连续变量，其余12个皆为名义变量。对于名义变量需要进行量化处理。为解决上述问题，本研究采用了One-Hot编码。

因为本研究的重点是评估贷款人是否存在违约风险，所以将贷款用户是否具有违约风险的结果作为信用风险评估模型的输出变量，记为y。将存在违约风险的客户记为1，将不存在违约风险的客户记为0。在建立个人信用风险评估模型之前，要先利用分层抽样和随机抽样来确定训练样本集和测试样本集。

4 实验研究

本研究实验平台为Intel(R) Core(TM) i5-4460 CPU， 8GB RAM， Windows 7操作系统，开发环境为Matlab R2012a，支持向量机软件LIBSVM。先进行参数设置。青蛙个体数为20，子蛙群数为2，子蛙群中局部迭代次数为2，混合迭代次数为50，允许青蛙更新的最大步长Dmax为1.2，惩罚参数C的搜索范围为[0.01，100]，核函数参数搜索范围为[0.01，100]。

实验目标函数为寻找最优分类准确率(CVA)，CVA越高，最佳适应度越大。图1为SFLA迭代曲线图，当SFLA进化到第10代时，此时误差达到最小，为8.6，CVA最高，蛙群中最佳适应度已经稳定在最大值。此时取得SVM最优C和g参数为47.596 5和23.925 0，其对应最优CVA为91.4%。由此可见，SFLA能够有效搜索SVM模型的C和g参数，寻优用时为30.073 6 s。

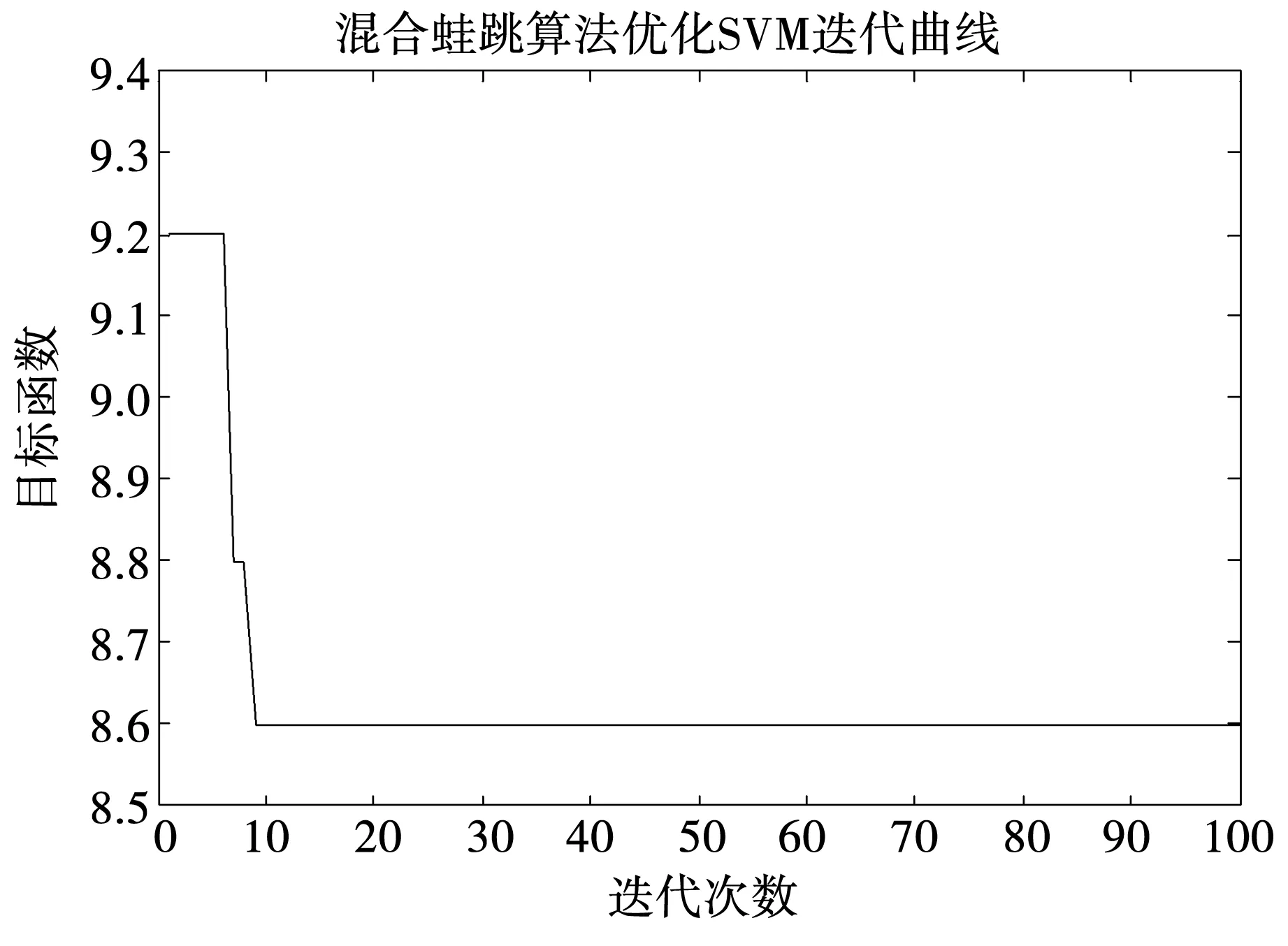
图1 SFLA迭代曲线Fig.1 SFLA iterative curve

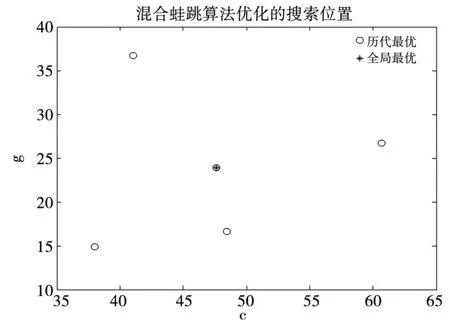
图2 SFLA优化(C,g)的搜索位置图Fig.2 Search location map of SFLA optimization (C,g)

图2为SFLA优化(C,g)搜索位置图。其中X轴为青蛙个体对超参数C进行的搜索范围，Y轴为青蛙个体对超参数g搜索范围。由图可见，历代青蛙个体对超参数C的搜索优化位置大都分布在[35，65]区域中，对超参数g的搜索优化位置大都分布在[10，40]内。

运用SFLA对SVM超参数进行寻优，取得了最优超参数组(C,g)，并与训练样本建立了基于SFLA-SVM的个人信用风险评估模型。为了检验该模型的性能，用该模型对测试样本进行了测试，测试准确率为90%。为了验证SFLA-SVM模型的优越性，保持实验数据不变，分别采用网格搜索法(Grid Search，GS)和遗传算法(Genetic Algorithm，GA)对SVM超参数C和g进行优化，并建立了GS-SVM模型和GA-SVM模型，进而对个人信用风险进行评估，得到的实验数据如表1所示。

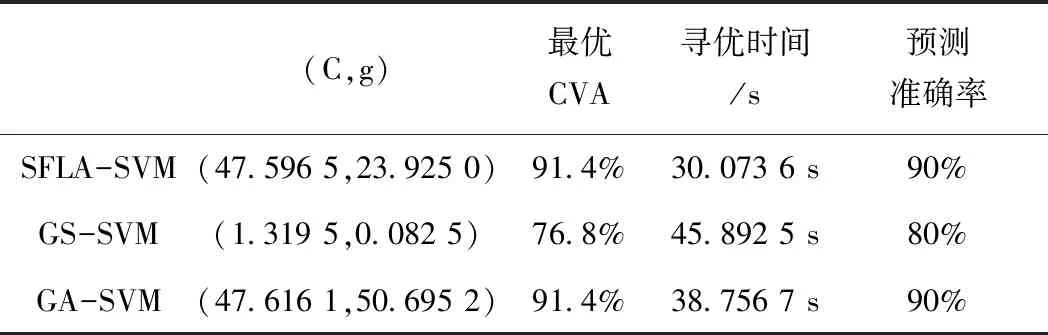
表1 SFLA-SVM、GS-SVM和GA-SVM模型实验数据对比Tab.1 Comparison of experimental data of SFLA-SVM, GS-SVM and GA-SVM

由表1可知，SFLA-SVM和GA-SVM模型在最优CVA、寻优时间和预测准确率三个方面都优于GS-SVM模型。混合蛙跳算法和遗传算法找到的最优CVA都为91.4%，对于测试集的预测准确率也都为90%。但从寻优速度来看，混合蛙跳算法比遗传算法要快，故基于SFLA-SVM模型的个人信用风险评估效果最好。

5 总结

本研究运用SVM模型对个人信用风险进行评估。因为SVM模型性能与其相关超参数的选取有着很大的关联，所以将SFLA引入到了SVM中来进行超参数的寻优，从而建立信用风险评估模型。为了验证该模型的性能，与在相同数据下建立的GS-SVM模型和GA-SVM模型进行信用风险评估的效果对比。结果表明，SFLA-SVM模型拥有更好的信用评估效果。