顶点赋权图中的连通子图划分问题
2020-09-18陈光亭
李 彤,陈 永,张 安,陈光亭
(1.杭州电子科技大学理学院,浙江 杭州 310018;2.台州学院电子与信息工程学院,浙江 台州 318000)
0 引 言
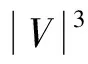
1 预备知识
给定一个简单顶点赋权连通图G=(V,E),设所有顶点的权重之和为W。对于V的任意2个顶点不相交的子集导出的子图G(V1)和G(V2),如果存在一条边(u,v)∈E,使得u∈V2且v∈V1,则说明V1和V2是相邻的。对于k-GP问题的顶点集V的任意一个可行划分,由于G是连通的,任何部分都至少与划分中的一个部分相邻。
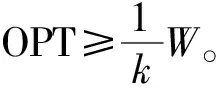
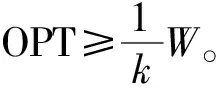
2 近似算法与算法分析

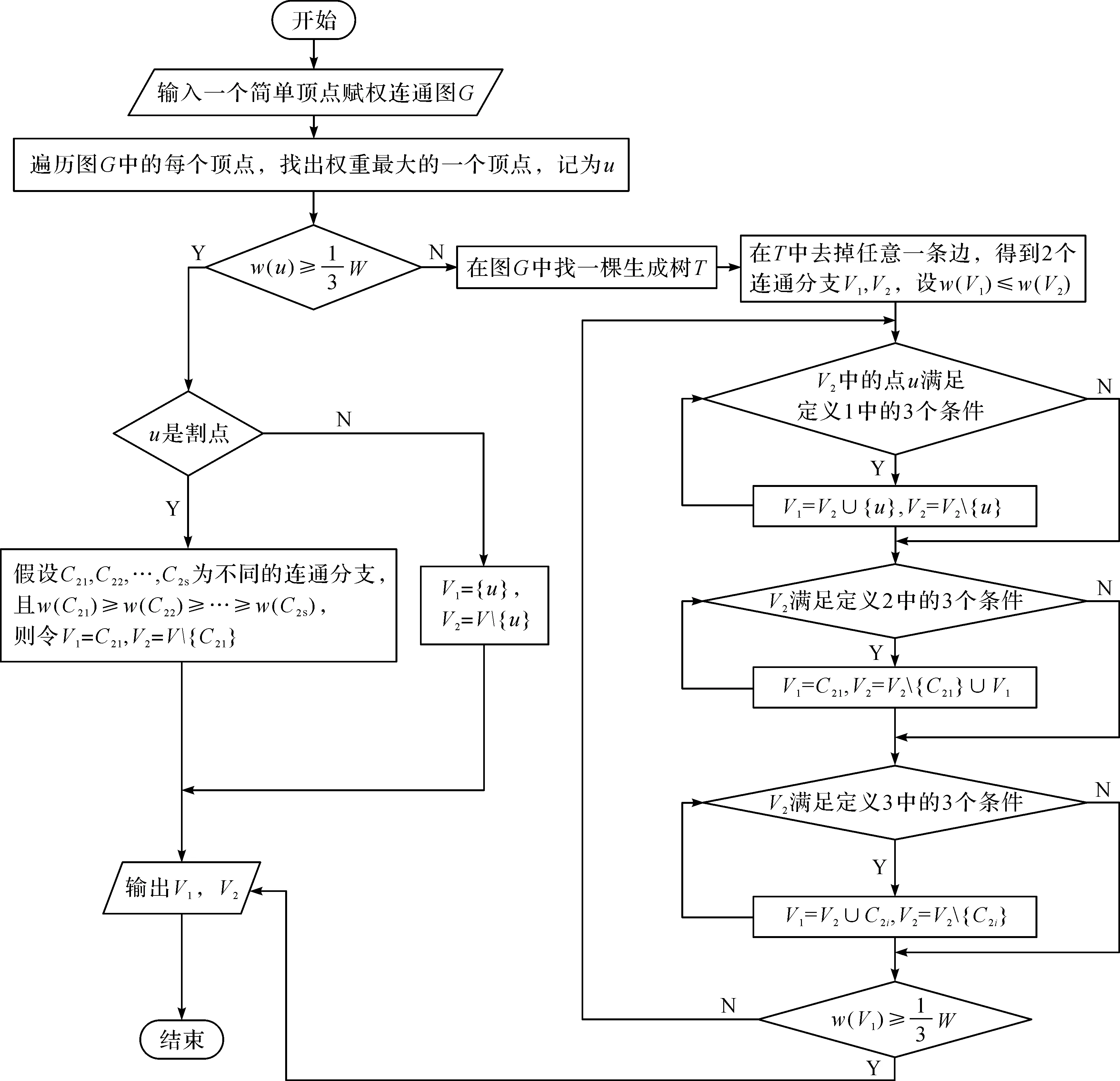
定义2如果V2满足:(1)V2中存在点u,u与V1之间有边相连;(2)在V2中,u同时连接若干个连通分支C21,C22,…,C2s,且w(C21)≥w(C22)≥…≥w(C2s);(3)w(V1) 本文提出的近似算法(简称:2-GP算法)思想如下:首先找到图G的一棵生成树T,再从T中任意删除k-1条边,产生k个连通分支V1,V2,…,Vk,w(Vi)表示第i个连通分支的权重,循环运用定义1至定义3的操作,逐步减小总权重最大子集的权重。算法的流程如图1所示。 图1 2-GP算法流程图 2-GP算法主要步骤如下: (2)在图G中找一棵生成树T。 (3)在T中去掉任意一条边,得到2个连通分支V1,V2,设w(V1)≤w(V2)。 (5)输出V1,V2。 引理2若定义1的操作不能进行,则在V2中u至少连接着2个连通分支。 引理3若定义2的操作不能进行,则w(V1)≥w(C21)。 证明因为图G是连通的,所以定义2中条件(1)成立。又由引理2可知,定义2中条件(2)成立。因此,定义2不能进行的原因是因为定义2中条件(3)不成立,即w(V1)≥w(C21)。证毕。 引理4若定义3的操作不能进行,则V1与V2中的连通分支均不相连接。 图2 最终图的划分结构 图3 算法紧例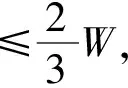





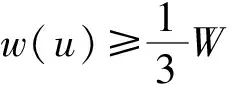


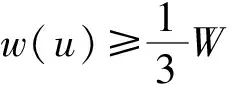

3 结束语

