HDMR模型在页岩气钻井投资测算中的应用
2020-09-18蒋雪梅刘玉涛
蒋雪梅 李 娟 谭 婷 刘玉涛 陈 超
(1.四川长宁天然气开发有限责任公司,四川 成都 610056;2.成都市精锐天诚信息技术有限公司,四川 成都 610051)
0 引言
2012年起,国家先后建立长宁-威远、昭通、涪陵等国家级页岩气示范区,工业化开采页岩气的序幕正式拉开[1-3],截至 2017 年建成了逾 100 × 108m3页岩气年产能力,页岩气年产量达90×108m3[4]。其中川南区块是我国页岩气资源贮藏最丰富、开发相对容易的区块[5-6],依据实际资源量测算,预测该区块可建页岩气年产能250~300 亿立方米,且稳产可达到20~30 年[7]。但是,页岩气开发开采面临着特殊的地质、地面环境以及更先进的技术装备要求等问题,投资居高不下是制约其工业化开采的主要瓶颈。其中钻井工程投资占勘探开发总投资的70%,直接影响投资效益[8]。另外,国外石油公司已采用信息化平台开展单井投资大数据分析,而国内公司大数据分析方法的研究运用较为滞后,传统数据处理模式(如比较法、因素分析法、差额计算法、比率法)[9]难以满足处理庞大数据的时效性、逻辑性和准确性要求[10-12]。笔者以川南地区页岩气的实际工程、经济及生产数据为基础,用数据分析方法,对单井投资进行深入剖析,通过借鉴大数据分析方法,研究模型输入量的不确定性对输出响应影响的灵敏度,以此摸清投资变化规律,寻找降本空间,并提出控制措施建议,使投资决策、预算管理及降本措施更具科学性和可操作性。
1 川南地区页岩气钻井投资分析
以川南地区A 页岩气区块结算72 口井费用参数为基础,根据钻井投资变化趋势分析各项目对投资影响的敏感性程度,研究变化规律,并有针对性地提出控制措施,为投资决策及控制提供依据。选取对工程造价影响较大的施工参数开展相关性分析,川南地区A 页岩气区块结算72 口井的主要施工参数及结算费用情况如表1所示。该区块页岩气井的钻井周期数据呈正偏态,平均86 天;平均井深4 678 m;水平段长数据集中分布于1 500 m左右;压裂规模平均1 908 m3,压裂段数峰度高集中分布于20 到25 之间,总体呈正偏态,部分井甚至超过40 段;单井结算费用平均为5 386万元。
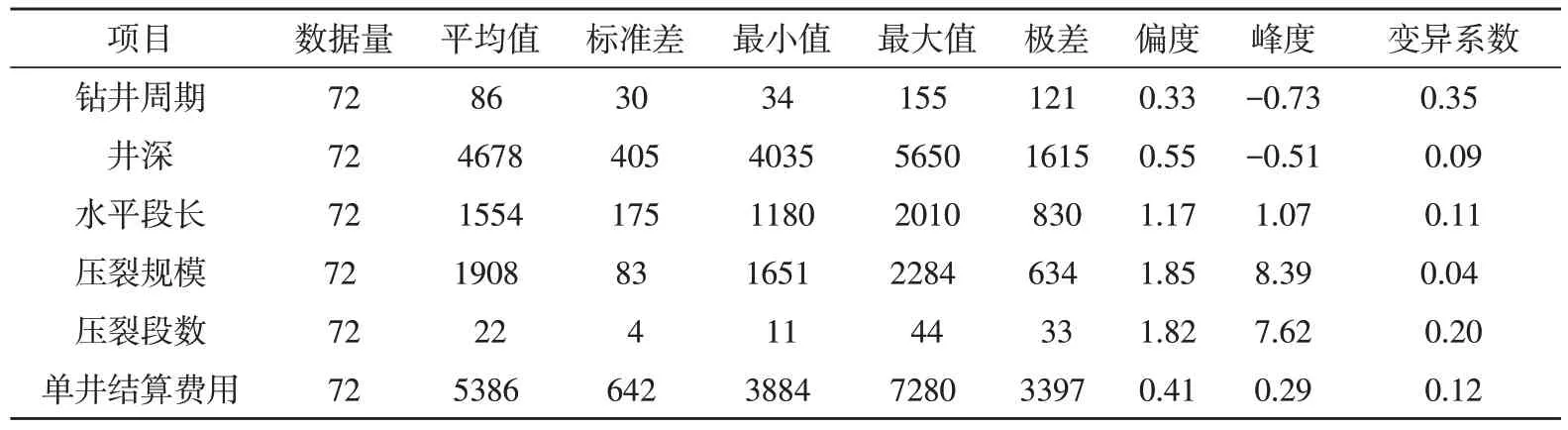
表1 施工参数与结算费用数据分布表
图 1 为以钻井周期(x1)、井深(x2)、水平段长(x3)、压裂规模(x4)、压裂段数(x5)和单井结算费用(y)等数据分别作相关性分析图。右上部分为变量之间的相关系数与显著评级,对角线部分为变量的数据分布,左下部分为变量间的散点图和拟合曲线。由图1可知钻井周期与井深、井深与水平段长、水平段长与压裂段数相关性最强,呈高显著的正相关关系;单井结算费用与五项因子间的相关性系数达到0.49。即钻井周期随着井深的增长而增加、总井深随着水平段的增长而增长,相应地压裂段数也增多,钻井周期、井深、水平段长、压裂规模、压裂段数均是影响工程造价的关键参数,能解释49%的单井总费用变化情况。
2 数据关系模型建立
多随机变量结构的灵敏度分析是求取具有高维输入变量的某一特定结构系统输出信息的过程,如果找到便捷方法能够取代大数据的重复计算,即可解决处理数据时的时效性问题[13-14]。其中HDMR 模型就可有效地表示出工程系统的输出响应与多维输入变量之间的映射关系,应用于结构多维不确定输入变量对系统输出量的影响研究,获得各函数因子对系统输出量的全局灵敏度信息[15-16]。
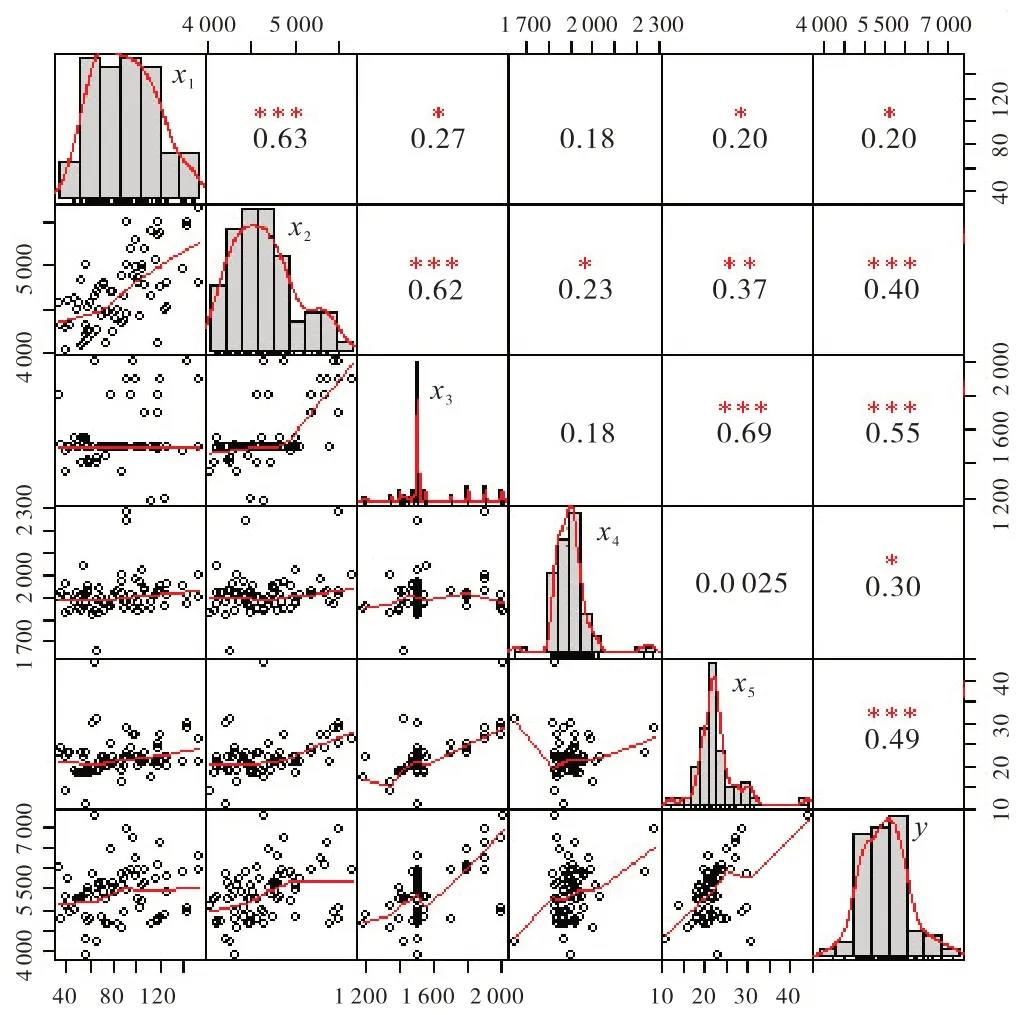
图1 钻井周期、井深、水平段长、压裂规模、压裂段数和单井总费用相关性分析图
2.1 HDMR模型建立
假设待解决项目设计变量的可行域为An(An∈Rn,Rn是n维实数空间),则输出函数f(x)∈R可由某个输入变量的独立影响和变量之间的耦合影响的层级叠加所表示。以钻井周期(x1)、井深(x2)、水平段长(x3)、压裂规模(x4)和压裂段数(x5)作为自变量,单井结算费用(y)作为因变量,则HDMR模型的一般形式如式(1):
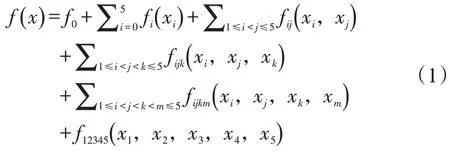
式中,f0是常数项,表示响应的零阶分量函数;fi(xi)是变量xi单独输入时对输出函数(fx)的影响,称为响应的一阶分量函数;fij(xi,xj)表示了变量xi和xj耦合作用输入时对(fx)的影响,称为响应的二阶分量函数;随后的各项表达式是指输入量增多的耦合作用对输出函数的影响。式(1)分别表达钻井周期(x1)、井深(x2)、水平段长(x3)、压裂规模(x4)和压裂段数(x5)各变量相互影响对单井结算总费用所产生的的效用。
一般项目中,变量间的关系通常显示为低阶耦合,高阶项的影响微乎其微。则输出函数f(x)可以简写为:
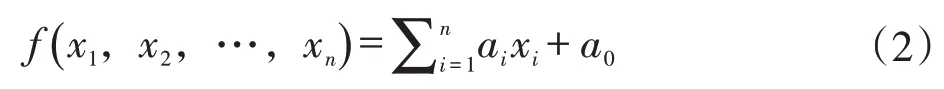
当应用HDMR 模型算法时,在可行域An内随机采样N个样本点,并通过正交基函数来确定HDMR的分量函数。生成一个(N,2k)随机数矩阵(k是输入参数的个数),定义两个矩阵(A和B),每个包含一半的样本,N称为基础样本;定义一个矩阵Ci,由B中除了第i 列的其他列组成,第i 列来自A中的第i列。随机数生成采取均匀分布,变量i的取值空间为[min(xi),max(xi)]。
2.2 基于方差分析的灵敏度分析
推导出HDMR 分量函数后,根据式(1)、式(2)对输出量进行方差分析,即可得到各函数对输出量的全局贡献灵敏度信息。
总方差D为:
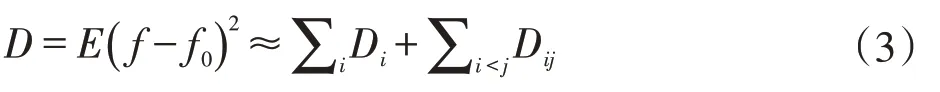
其中的分量方差成分为:

即总方差是各分量方差的和。据此公式,可定义输出值受各耦合分量影响的全局灵敏度因子[17]。

式中:Si为一阶全局灵敏度因子;Sij为二阶耦合灵敏度因子。
一阶全局灵敏度因子指示了每个输入参数对输出变化的主要影响贡献。依据前述随机数矩阵取样方法,第i个变量的一阶全局灵敏度因子可表示如下:

总灵敏度因子指示了计算参数Xi对输出方差的总贡献,如它的一阶效应加上二阶耦合效应,则第i个变量的总灵敏度因子为[18]:
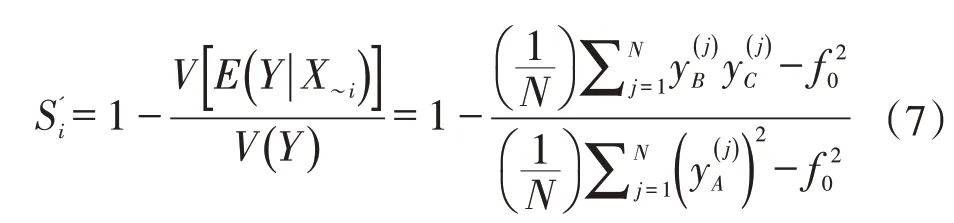
据此模型开展方差分析,得到各分量函数对模型输出响应的全局灵敏度信息。将获得的一阶全局灵敏度因子进行对比,考察5个变量对模型输出量的影响程度,即可明确单井结算费用的主要影响因素。
2.3 HDMR模型拟合及结果分析
由于HDMR 并不是唯一的,所以对总样本采用交叉拟合的方法,得到94 组通过验证的HDMR 模型,对模型得到的系数进行分析(表2)。
2.4 HDMR模型结果分析
该94组HDMR模型的平均拟合优度为0.8并通过模型检验,可得出HDMR 模型基本都是有效的(表3)。项目的灵敏度与其样本数据的变异系数相对大小成正比,说明灵敏度分析是可靠的。所建立的HD⁃MR 模型中,全局灵敏度因子数值越大,说明其对单井结算总费用的影响越明显。即单井结算总费用对钻井周期和压裂段数灵敏度最高,二者的总灵敏度因子和为93%,说明两者是影响单井总费用的最主要因素,其余影响因素的大小顺序为钻井周期>压裂段数>水平段长>井深>压裂规模,且该HDMR 模型能解释80%的单井总费用变化情况。
3 HDMR模型验证
从川南未结算井中随机选取20 口井来验证HD⁃MR模型的有效性。对单井投资概算进行分部分项工程分解,并对钻井周期、压裂段数、水平段长、井深和压裂规模5 个关键影响因子的相关性进行标定,汇总与各影响因子相关的分部分项工程费用即可求得与该影响因子相关的总费用以及占单井投资的比例。统计结果显示5个工程参数相关的分部分项工程费用占单井投资总费用为78.5%,其中钻井周期、压裂段数、水平段长、井深和压裂规模分别占比22.2%、20.0%、16.3%、11.7%、8.4%(表4),钻井周期、压裂段数是最显著的影响因子,这与HDMR 模型得到的参数影响规律基本吻合,即基于HDMR 模型的数学分析方法可有效确定项目成本变化的主控因素,并定性地测算各因素的影响程度。
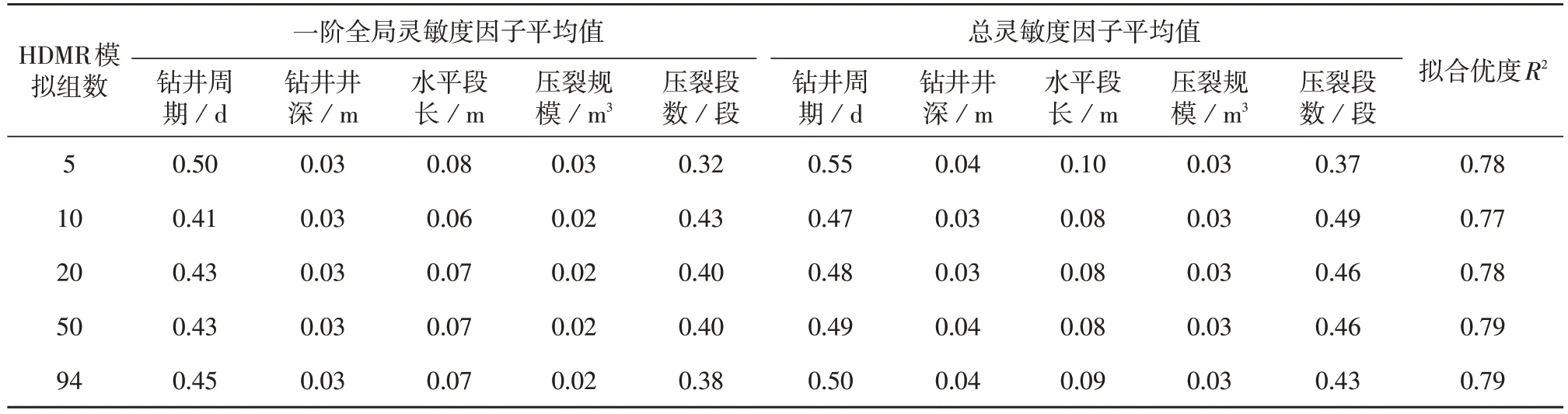
表2 不同模拟组数系数分布表

表3 全局贡献灵敏度信息表(n=94)

表4 未结算井关键工程参数影响因子相关费用占比(n=20)
4 结论及建议
1)针对四川盆地国家级页岩气示范区,钻井投资居高不下是制约其规模开发的主要瓶颈,从川南地区页岩气开发现状出发,分析钻井投资影响因素,研究钻井投资控制措施,对保证页岩气勘探开发投资效益和企业可持续发展具有重要意义。
2)以川南地区A页岩气区块结算72口井的施工参数及结算费用为基础,通过数据相关性分析及构建HDMR 模型,可以较好地解释80%的单井总费用变化情况。其中钻井周期和压裂段数的总灵敏度因子达93%,是单井总费用的主要影响因素,其影响因素的顺序为钻井周期>压裂段数>水平段长>井深>压裂规模。
3)控制页岩气钻井投资是实现页岩气商业开发的关键,依据模型分析结果控制投资的核心是缩短钻井周期和降低压裂施工成本,则提高钻井效率和优化压裂工程量是主要措施方向。建议重点发展小井眼技术并优化压裂改造工艺,探索并建立适合我国地质特征的页岩气勘探技术体系;同时利用钻井工程投资大数据平台开展模型分析,构建有效的页岩气开发投资管控体系的有效途径。
