矿区非线性沉降的GM(1，1)预计残差改进模型及应用

2020-09-18阎跃观代文晨牛永泽谯震

矿业科学学报 2020年5期

阎跃观，代文晨，牛永泽，谯震

中国矿业大学(北京)地球科学与测绘工程学院，北京 100083

矿区地下开采活动引起的地表移动和变形会对地表铁路、公路及建筑物的安全造成不可忽略的影响。基于GNSS技术和水准等测量方法对矿区地表沉降情况进行长期、连续的监测，并及时预测未来一段时间内地表沉降趋势，对保证井下安全生产和地表建(构)筑物安全具有重要意义。目前常用的预测方法主要有Logistic曲线模型、Gompertz曲线模型、Asaoka曲线模型、马尔科夫模型和 GM(1，1)模型等[1]。基于灰色理论的GM(1，1)模型能够解决贫信息的问题，通过挖掘数据内部潜在信息，从而达到高精度预测[2]。为此，近年来许多学者对GM(1，1)模型在沉降监测中的应用进行了研究[3-9]。陈俊杰等[3]利用MATLAB软件对测量数据进行等时序化处理，使用GM(1，1)模型求得概率积分法参数并进行了相关分析；李庆勇等[4]建立了非等间距GM(1，1)模型，并通过实际应用证明了GM(1，1)模型在矿区沉降监测中具有良好的精度；刘云生[5]对数据进行加权改进，扩大了GM(1，1)模型的适用性；彭正明等[6]基于二次拟合优化方法建立了GM(1，1)改正模型，并在实际应用中取得了较好的效果；龚祖官等[7]提出一种采用卡尔曼滤波对原始序列降噪和利用辛普森公式改正背景值的动态GM(1，1)模型，并通过实例证明动态GM(1，1)模型预测精度优于GM(1，1)模型；赵泽昆等[8]提出了时间加权-新陈代谢GM(1，1)模型并应用于建筑物沉降预测，证明了该模型预测精度高于传统GM(1，1)模型；陶武勇等[9]提出了一种适合非等间距GM(1，1)模型求解的总体最小二乘算法，并改善了GM(1，1)模型中的病态问题。

大量研究证明，GM(1，1)模型可用于建筑物和矿区地表沉降预测。但是，在矿区地表沉降监测中，地表移动持续时间长，因而具有长时序的外业观测数据特征，且地表沉降趋势和下沉速度均表现为非线性的变化，导致GM(1，1)模型在矿区沉降监测应用中有以下两个方面的局限性：一是矿区地表非线性沉降增大了GM(1，1)模型的模型误差，降低了预测精度；二是在长时序数据中难以选取合适的数据区间。数据区间的选择对模型精度和预测精度有重要的影响，但是目前关于建模数据时序区间选取的研究尚不多见。

为解决上述问题，本文通过分析矿区地表非线性沉降特征，建立了GM(1，1)预计残差改进模型，提出了适用于矿区沉降预测的建模数据区间选取方法、建模预测流程和模型精度评定标准，并进行了实例验证。

1 矿区地表非线性沉降特征分析

地下煤层开采引起的上覆岩层和地表移动变形，影响地面建(构)筑物的安全。通常，用地表下沉速度反映地表移动的剧烈程度，地表下沉速度越大，地表移动变形越剧烈。在开采过程中，煤层倾角小于45°时，依据下沉速度把地表移动变形过程划分为3个阶段[10-11]。

(1) 开始阶段：地表累计下沉量达到10 mm至下沉速度达到1.67 mm/d。

(2) 活跃阶段：地表下沉速度大于1.67 mm/d。

(3) 衰退阶段：地表下沉速度小于1.67 mm/d至地表下沉累积量(6个月内)不超过30 mm。

地表的下沉量主要集中在活跃阶段，此阶段的下沉量占总下沉量的85%以上[12]。

依据上述3个阶段作出地表移动阶段的速度变化曲线图(图1)。图中，区间Ⅰ对应开始阶段，区间Ⅱ和Ⅲ对应活跃阶段，区间Ⅳ对应衰退阶段。

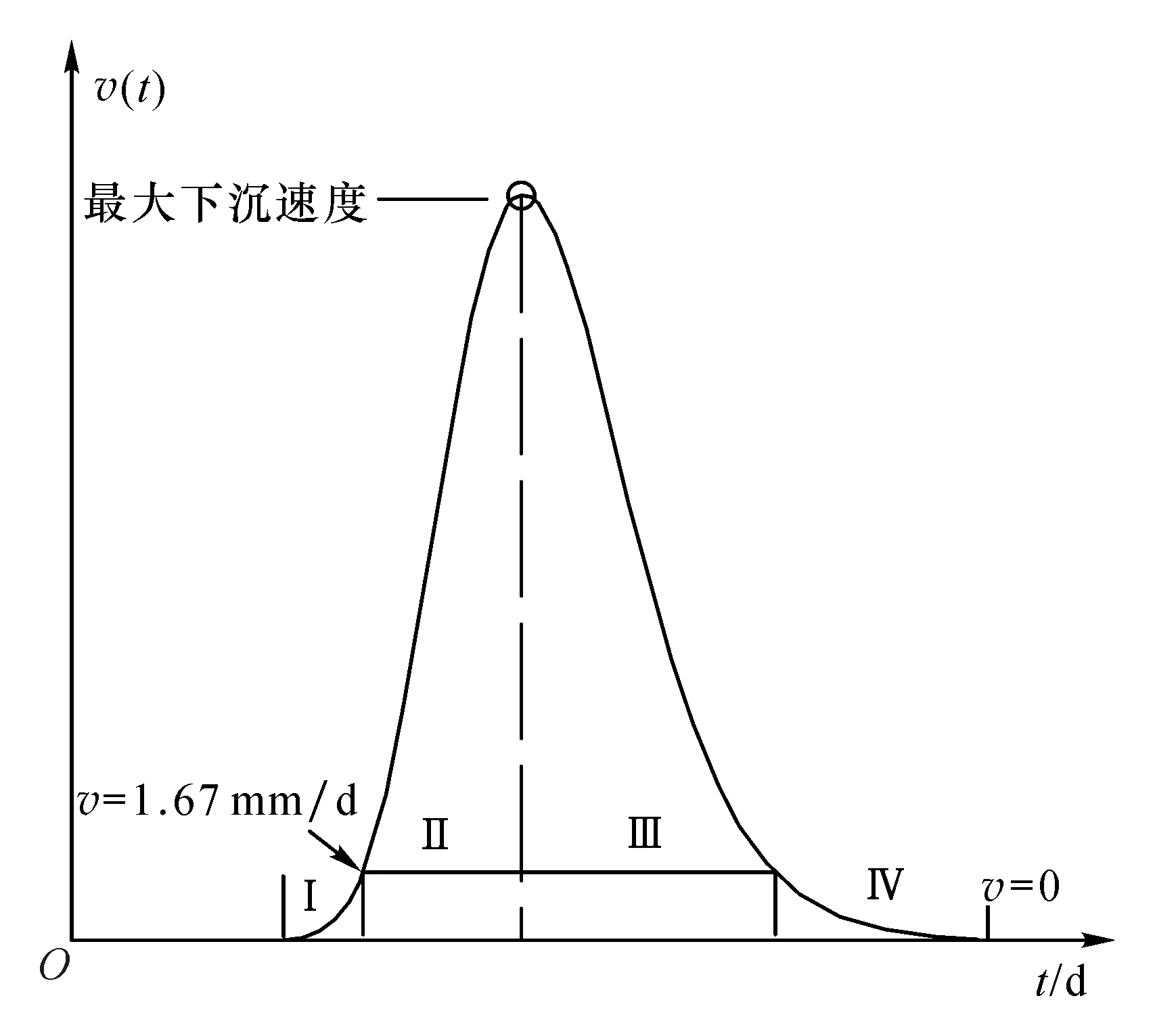
图1 地表移动阶段示意图Fig.1 Sketch map of surface movement stage

当煤层倾角大于45°时，划分地表移动阶段的下沉速度为1 mm/d[10]。

由图1可以看出，在地表移动过程中，下沉速度的变化在时间上是连续的：区间Ⅰ内下沉速度较小，始终小于1.67 mm/d；区间Ⅱ内下沉速度由小逐渐增大，直到最大值；区间Ⅲ内，下沉速度从最大逐渐减小，直到1.67 mm/d；区间Ⅳ中下沉速度也是逐渐减小，地表下沉趋于稳定。由分析可知，地表点下沉速度总体表现为先增大后减小的非线性变化特征，相应的地表沉降也表现为非线性变化。由图1还可看出，四个区间内的下沉速度变化趋势各不相同，地表下沉加速度在区间Ⅰ内由小逐渐增大，在区间Ⅱ中期附近达到最大(记作tamax)然后开始减小，在速度达到最大时(记作tvmax)减小为零；区间Ⅲ内下沉速度开始减小，此时加速度由0开始相对于区间Ⅱ反向逐渐增大，在区间Ⅲ中期附近达到最大后加速度逐渐减小；区间Ⅳ内下沉速度越来越小，加速度也是逐渐减小。因此，在矿区地表非线性沉降监测中，可以参考当前时刻所属阶段的下沉速度和加速度变化特征选取数据进行建模预测。

2 GM(1，1)改进模型及精度评定

在预测工作中，一般都是先通过探究已有观测数据的变化规律确定合适的模型并进行预测[13-18]。但是在非线性沉降的矿区地表监测中，始终受到模型误差的困扰。为减小建模误差对预测结果的影响、提高预测精度，本文建立了GM(1，1)预计残差改进模型，对模型残差进行加权改正，同时提出了针对矿区地表非线性沉降的建模数据区间选取方法、建模预测流程和模型精度评定标准。

2.1 GM(1，1)改进模型建立

受测量环境和天气等因素影响，很难确保外业测量数据为严格的等时间序列，因此建模之前需要对实测数据作等时序化处理，并将高程值转换为累计下沉值作为建模数据。

(1) 对所选取的建模数据进行累加处理。由

x0(m)，x0(m+1)，x0(m+2)，…，x0(n)

得

x1(m)，x1(m+1)，x1(m+2)，…，x1(n)

其中

m>>1，n>>m+3

(2) 建立白化形式微分方程。将累加处理结果对时间t求一次偏导，得

(1)

式(1)记为GM(1，1)。其中，a、u为灰参数，其白化值(灰区间中的一个可能值)为

(3)利用最小二乘法求解微分方程：

(2)

Yn=[x(0)(m+1)，x(0)(m+2)，…，x(0)(n)]

(4) 对模型误差加权改正，得到改正后残差：

(3)

k=m，m+1，m+2，…，n

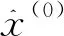
(5) 将式(2)代入式(1)得到时间函数，经过累减处理和残差改正，建立GM(1，1)改进模型。

2.2 建模区间的选取和预测流程

2.2.1 建模数据区间选取方法

针对矿区地表移动持续时间长、具有长时序的外业观测数据、下沉速度和地表沉降均表现非线性变化的特点，提出了先阶段后截尾的建模数据选取方法。该方法先按照下沉速度划分阶段，再依据速度的变化趋势即加速度确定建模数据区间选取。

设时刻ti、tj、tk、tl分别位于Ⅰ、Ⅱ、Ⅲ、Ⅳ四个下沉阶段，tamax为阶段Ⅱ中期附近的最大加速度时刻，tvmax为最大下沉速度时刻，t-amax为阶段Ⅲ中期附近的反向加速度最大时刻。

已知当前时刻ti处于下沉阶段Ⅰ内，根据阶段划分标准和下沉速度变化曲线，可以确定ti时刻的下沉速度小于1.67 mm/d，且下沉加速度小于1.67 mm/d2，地表沉降量较小，按照GM(1，1)模型建模最低要求，只需截取最后4次数据(ti-3，ti-2，ti-1，ti)进行建模预测。

时刻tk位于活跃阶段Ⅲ内且tvmax<

时刻tl位于衰退阶段Ⅳ内，下沉加速度小于1.67 mm/d2且下沉速度小于1.67 mm/d，该阶段的地表下沉量也比较小，截取该阶段最后4次数据建模预测。

当下沉加速度达到最大后逐渐减小趋近于0时，下沉速度即将达到最大，此时截取tamax，…，tj-1，tj区间(对应)的数据进行建模预测，同时还可以加密观测次数，以保证矿区安全生产和为探究地表移动规律提供充足数据。

2.2.2 GM(1，1)改进模型的预测流程

(1) 利用MATLAB软件对数据进行插值处理，得到等时序的累计沉降数据。

(2) 计算下沉速度，并依据下沉阶段速度标准划分为相应的阶段。下沉速度计算公式：

式中，v为地表下沉速度；Δh为Δt时间内的高程变化。

(3) 根据建模数据区间选取方法，确定建模数据区间。

(4) 根据2.1节建立的改进模型进行建模、模型残差加权改正。

(5) 模型精度评定和进行预测。

2.3 模型精度评定

GM(1，1)模型常用的模型精度评定方法主要有残差检验、关联度检验和后验差检验3种[19-24]。GM(1，1)改进模型精度评定标准由相对误差Q、后验差比值C和小误差概率P共同确定。评定过程如下：

(1) 计算残差e(k)。

k=m，m+1，m+2，…，n

(2) 计算原始序列x0(k)和残差e的方差s12和s22。

(3)计算相对误差Q、后验差比值C和小误差概率P。

C=s2/s1

P={|e(k)|<0.6745s1}

(4)按照表1内容对模型进行精度评定。模型精度等级按下式确定：

模型精度等级=max{Q所在的级别，P所在的级别，C所在的级别}

表1 精度检验等级参照

3 实例应用分析

为探究我国西部矿区地表沉降动态变化规律，对某矿工作面的走向和倾向观测线进行长时间的外业观测。本文以该工作面走向线Z16号监测点为例，探讨GM(1，1)模型和GM(1，1)预计残差改进模型的精度，验证建模数据区间选取方法的有效性。首先，利用MATLAB工具对观测数据作插值处理，得到了Z16号监测点26期等时序的累计沉降数据序列(表2)，时序代表初始观测后的观测次数，时序26对应的累计沉降量为348.1 mm。然后，按照建模预测流程分别使用GM(1，1)模型和GM(1，1)预计残差改进模型进行建模预测，得到 GM(1，1)模型和GM(1，1)改进模型的相对误差Q、后验差比值C和小误差概率P等精度参数。

由表2可知，时序11对应的累计沉降量 10.2 mm，地表移动已处于开始阶段，利用GM(1，1)模型和GM(1，1)预计残差改进模型分别对相同区间的数据(以区间11-25为例)进行建模预测。上述建模对应的建模数据区间长度、预测结果和残差相对误差等结果见表3。此外，由于当前时刻位于活跃阶段Ⅱ内且时序数据少，利用试验法对区间11-25内的所有数据依次进行建模，探讨不同建模数据区间和模型精度的关系和验证建模数据区间选取方法的有效性，各个区间对应的模型精度参数和预测值等结果见表4。

表2 Z16号监测点等时序累计下沉观测数据

表3 GM(1，1)模型和GM(1，1)改进模型预测结果

表4 对不同区间数据的建模预测结果

由表3可知，通过对同一区间11-25建模，GM(1，1)预计残差改进模型的预测残差比GM(1，1)模型小17.1 mm，相对误差减小了4.9%。可见，GM(1，1)预计残差改进模型精度优于GM(1，1)模型。

比较表4中建模数据区间11-25和区间 14-25对应模型精度和预测结果可得，模型精度的Q、C和P都得到了提高，模型精度提高10%，预测精度提高约5%。由建模数据区间14-25至22-25的结果可得，随着建模数据区间长度减小，相对误差Q由22.5%降至0.9%，后验差比值C由0.17降至0.03，模型误差由23.9%降低到0.08%，模型等级由“不合格”变成“好”，模型精度得到了显著提高，证明了建模数据区间选取方法的有效性。此外，还计算了建模数据区间长度与模型精度的相关性，相关系数为0.98，证明建模区间长度和模型精度具有很强的相关性，建模数据区间越短，数据距离预测时刻的时间距离越小，更能真实反应数据的变化趋势。