万有引力与距离平方成反比的牛顿式几何证明——解读经典之《自然哲学的数学原理》

王 磊 陈建文

(1. 盘锦市高级中学，辽宁 盘锦 124000； 2. 盘锦市辽东湾实验高级中学，辽宁 盘锦 124000)

1 引言

天体运动是高中物理必修2的内容，天体运动首先从开普勒的三大定律讲起.在匀速圆周运动模型下，将开普勒第三定律与圆周运动理论结合即可推导出牛顿万有引力公式.哈雷、胡克等物理学家就是基于这样的方法推测太阳对行星的引力与距离平方成反比.但我们知道万有引力的发现最终还是归功于牛顿，因为只有牛顿完整的证明了在距离平方反比的中心力场下物体的运动为椭圆.

在好友哈雷的帮助下牛顿于1687年出版了他的划时代巨著《自然哲学的数学原理》(以下简称《原理》).在书中，牛顿详细的用带有微分思想的几何方法论述了平方反比中心作用力下物体的运动轨迹为椭圆，这部分是《原理》一书中最精彩内容之一.其中涵盖了大量的椭圆几何问题与微分极限方法.《原理》成书虽已300余年，其用到的几何知识与微分思想也基本涵盖在高中范围以内.但我国读者想读懂《原理》一书并不容易.一方面，牛顿模仿欧几里得的《几何原本》书写方式，原理套原理，引理引引理，关于引力的平方反比的证明，作者为了成书的完备性从最初的几个命题证明了几十个定理与引理，持续近半部书的证明使得读者难以找到清晰的逻辑链条.另一方面《原理》书原文为拉丁语，在后人将其用拉丁语译为英语，传入我国再译为汉语的翻译过程中失真现象比较严重，当下主要几版译书在该部分内容相关的如“正矢”、“纵坐标”等译文以及相关配图出现严重问题，让读者摸不着头脑.《原理》一书中无论是牛顿开创的微分、极限思想，还是其高超的几何能力都值得学生们仔细品读.

2 牛顿对于万有引力平方反比的论述

2.1 弧的“正矢”正比于时间平方

图1

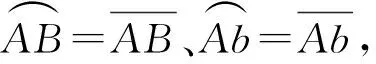
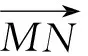
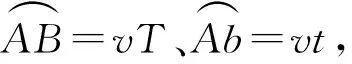
2.2 弧的“正矢”正比于引力

图2

因为Cc平行于SB，有△SBc面积等于△SBC面积，又△SAB面积等于△SBc面积，可得△SAB与△SBC面积相等，相同方法下可得△SAB、△SBC、△SCD、△SDE、△SEF面积皆相等，由此可知每隔相同时间给运动物体以指向某一特定点S的冲量时，在该相同时间间隔Δt内，该定点与物体的连线扫过的面积相等，即定点S与物体连线扫过的面积与时间成正比，或者反过来说时间与面积成正比.

2.3 椭圆轨道下引力平方反比证明

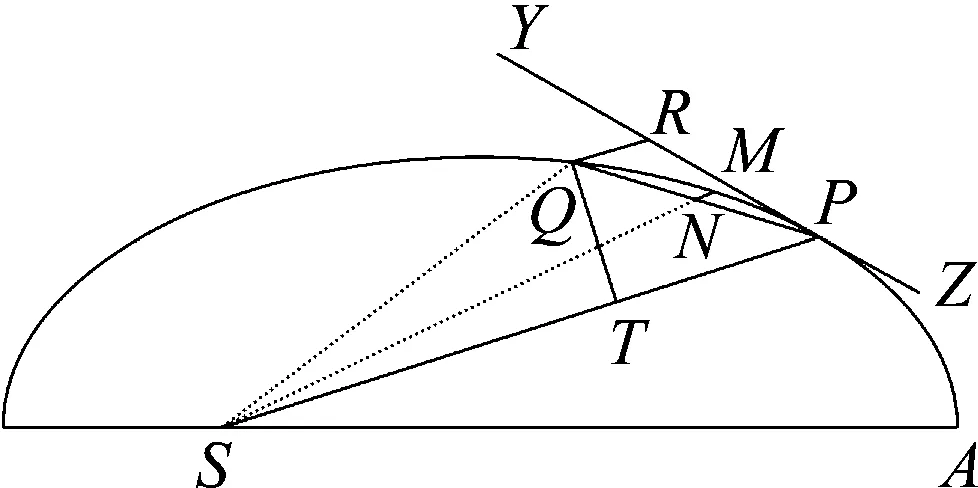
图3

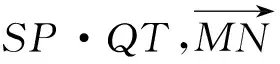
图4

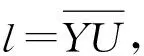
(1)

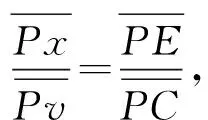
(2)

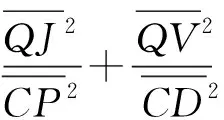
(3)

(4)