错列圆柱的三维大涡模拟

汪 洋,陈 立

(四川省公路规划勘察设计研究院有限公司，四川成都 610000)

斜拉索、电缆等钝体结构由于其柔度大、阻尼小易导致各种风致振动问题，对于这类问题一般将结构简化为圆柱模型进行研究[1-5]。圆柱绕流是流体力学中的经典问题之一，当粘性流体流经钝体时，会发生边界层分离现象，进而在尾部形成周期性涡脱，同时伴随着钝体两侧壁面压力的变化，从而对结构产生有规律的气动力作用。特别对于双圆柱绕流的情况，圆柱间的耦合干扰作用会导致其气动力特性有别于单圆柱绕流，因此双圆柱绕流问题一直是专家学者研究的热点[6-10]。

大部分研究集中在串列圆柱绕流上。Zdravkovich认为串列圆柱之间的流体流动形态与柱间中心距有关，当两圆柱中心距为1.0D～1.5D时，上游圆柱分离出的自由剪切层会越过下游圆柱；当两圆柱中心距为1.5D～4.0D时，剪切层会附着在下游柱体上；当中心距大于4D时，上游和下游柱体会分别形成涡脱，其中D为圆柱直径。Kitagawa运用大涡模拟研究了Re=22000时不同中心距下的串列圆柱，结果表明：当中心距小于3.25D时，只有下游圆柱出现漩涡脱落；当中心距大于3.25D时，上下游均发生涡脱现象，并且发现中心距在3.25D附近时，上下游的平均阻力系数和升力系数会发生跳跃性变化。Tokoro与Komatsu的理论研究与风洞试验表明:当串列圆柱中心距为4.3D风向角为15 °时，下游圆柱会出现明显振动。Brika和Lanevill采用风洞试验的方法对中心距为10D～25D的串列双圆柱进行了远距失稳现象的研究。也有少部分学者对并列圆柱的绕流特性开展了研究，Sumner[15]分别对小中心距(1.0D～1.2D)、中等中心距(1.2D～2.2D)、大中心距(>2.2D)的并列圆柱绕流进行了分析。在实际工程中，钝体的布置形式相对于流体流动方向一般都是错列的，然而错列双圆柱的绕流状态却很少受到研究者的关注。

本文采用大涡模拟的方法对Re=3900中心距3D的错列双圆柱绕流进行数值模拟，得到了不同风向角下的升阻力系数、尾流相对速度以及风压系数等参数，并分析了下游圆柱升力系数出现极大值的原因。

1 错列双圆柱绕流数值模型

1.1 计算工况

风向角α的范围为0～24 °，角度从0 °开始每2 °设置一个工况，一共13个工况，圆柱相对中心距W=3.0D(图1)。

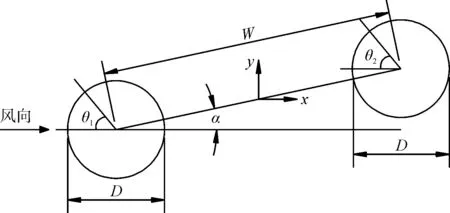
图1 圆柱布置示意

1.2 计算域与边界条件

计算域设置为：流向长度20D，横向长度10D，展向长度3.2D，以保证湍流尾流的充分发展。计算区域划分为三个部分，均采用结构化网格：第一部分为3D×3D×3.2D矩形近模型区域，该区域为加密网格区，越靠近圆柱网格的密度越大，第一层网格到壁面的距离为2×10-4m，Y+值约为0.8；第二部分为直径9D的圆形区域，方便在调整工况时改变风向角；第三部分为外围计算域，适当降低网格密度以节省计算机资源。形成的网格见图2，模型的总网格数量达到182×104个。

图2 计算域网格划分

计算域左侧为速度入口，流速为U0=0.57m/s；右侧为压力出口；上下前后流域边界为对称边界；圆柱表面为无滑移壁面。

坐标系选择：双圆柱中心连线的中点作为坐标原点，x轴方向与来流方向一致，y轴垂直于计算域上下边界，z轴由右手定则确定。

1.3 参数设置

流体为空气，密度ρ=1.225 kg/m3，动力粘度μ=1.7894×10-5pa·s。亚格子尺度模型采用WALE模型，压力速度耦合求解算法采用对大多数问题都适用的SIMLPE算法，梯度离散采用节省计算量的最小二乘法，压力离散格式采用标准格式，动量离散格式采用具有高阶格式的有界中心差分格式。瞬态求解时时间步长Δt=0.005s，以保证库朗数小于5且每个时间步迭代收敛。

1.4 网格独立性验证

为验证网格独立性，对雷诺数Re=3900的单圆柱在同样的网格参数(计算域尺寸、网格密度、时间步长与错列圆柱模拟相同)条件下进行了数值模拟，并与Lourenco[17]与Norberg[18]的风洞试验进行对比。从图3与图4中可见时均速度与表面压力系数的曲线与试验曲线吻合较好。

图3 单柱平均流速

图4 单柱压力系数

2 模拟结果

2.1 尾流平均风速

在中心平面上(z=0)本文选取了3个剖面来监测尾流平均风速，分别是x/D=0，x/D=2.1，x/D=3。因工况较多，本文仅列出风向角α=0°与α=24°情况下的模拟结果。

图5给出了α=0°时平均流速沿y轴的分布规律。从图中可以看出速度关于x轴对称，这与结构的对称性相一致，随着湍流的发展，速度分布曲线的形状由“U”形逐渐变为“V”形，说明湍流尾流在周边流体的影响下，速度逐渐趋近于周边流体的速度。在y=0处，速度大小出现极小值，风速大小从圆柱中心向两侧迅速增长，快速增长区域大约为2D，之后风速趋于稳定。图6为α=0°平均流速云图，可以直观地看到下游圆柱完全浸没在上游圆柱的尾流之中，气流在圆柱之间形成了较大范围的回流区，在下游圆柱尾部也形成了长度约为1D的回流区。

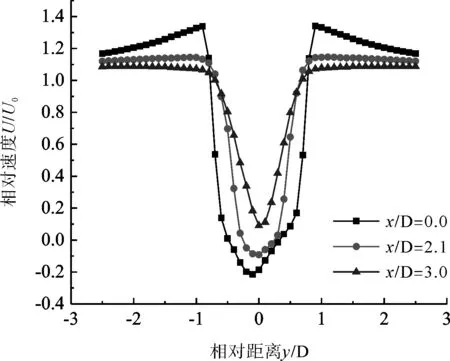
图5 α=0°平均流速分布

图6 α=0°平均流速云图

图7给出了α=24°时平均流速沿y轴的分布规律。由于圆柱对气流的阻挡作用，在y方向上与圆柱位置对应处的流速会出现两个极小值，下游圆柱尾流流速的极值出现在圆柱的正后方，而上游圆柱尾流因为间隙流的挤压效应，速度极值的出现位置会向y轴负向偏移。图8为α=24°的平均流速云图，下游圆柱不再浸没在上游圆柱的尾流之中，圆柱之间出现间隙流并分别在尾部出现回流区，下游圆柱回流区长度约为1.5D，上游圆柱回流区略小于上游圆柱，长度约为1.3D。

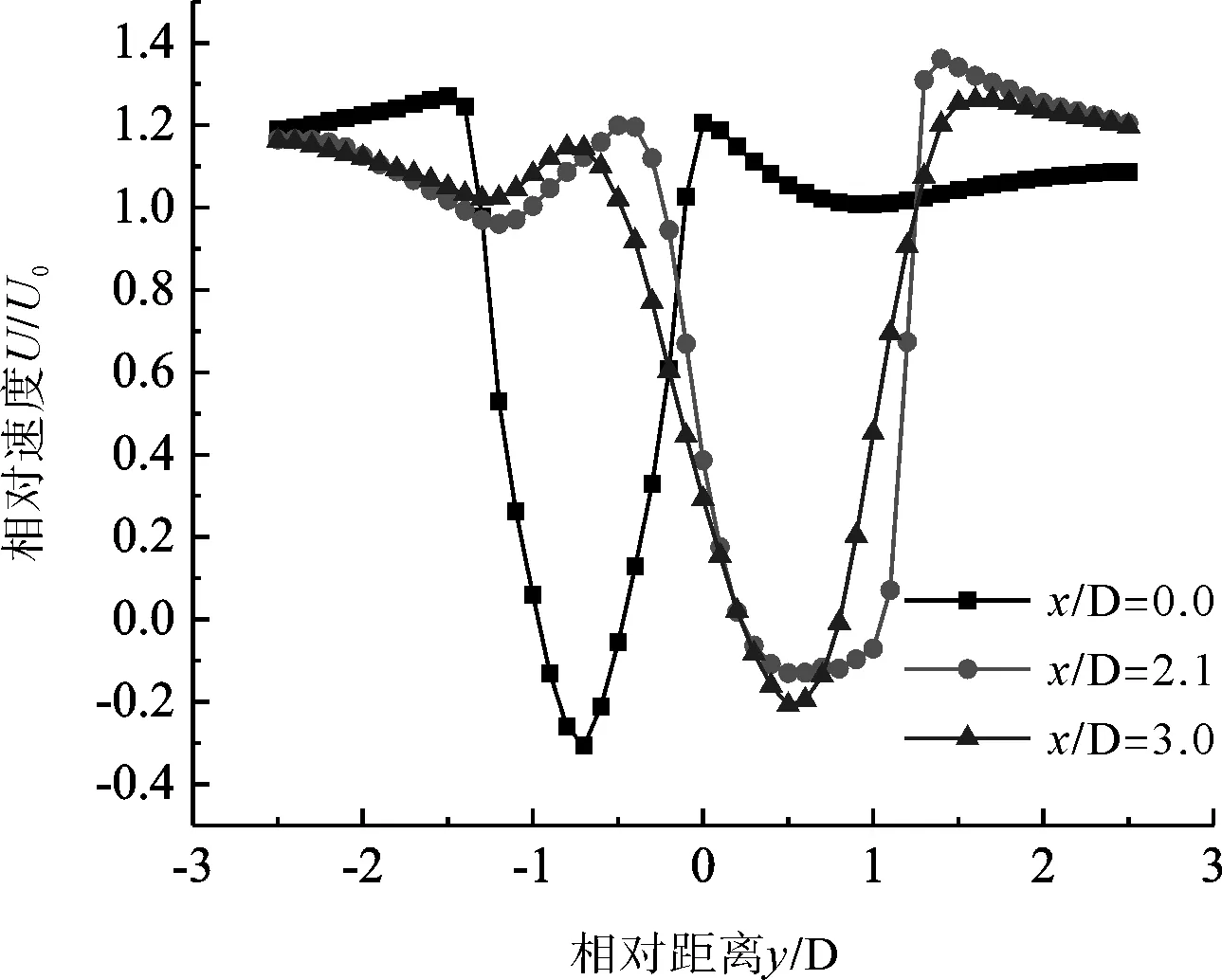
图7 α=24°平均流速云图

图8 α=24°平均流速云图

2.2 平均风压系数

沿圆柱周向布置36个监测点，监测点间隔为10 °。图9为α=0°时的圆柱时均压力系数分布。从图中可以发现上游圆柱表面正对来流处(θ1=0°)的压力系数最大，大约为1.0。随着气流向圆柱两侧扩展，Cp值迅速减小，并逐渐转变为负压，在θ1=70°处达到最大负压，大约为-1.0，说明气流边界层在该处与上游圆柱分离，分离角θsep=70°，边界层分离后压力系数Cp逐渐回升并增大到一个较为稳定的值，在圆柱背后形成稳定的负压分布；下游圆柱受到柱间回流区域的影响，表面压力系数均为负值，θ2=30°与θ2=330°处的负压值最大，最大负压值约为-0.77，在θ2=70°与θ2=290°处负压值最小，最小值为-0.14，说明气流从上游圆柱分离之后在该处进行了再附，随着气流向圆柱后方延伸，负压值略微增大之后趋于稳定，并在下游圆柱后方形成稳定的压力分布区域。

图9 α=0°平均风压系数

图10为α=24°时的圆柱时均压力分布。在正对来流处(θ=0°)两圆柱的压力系数最大，最大值均为0.25。随着气流在圆柱壁面上的流动，压力系数迅速减小，并逐渐转变为负压，上游圆柱的气流分离角为70 °与290 °，在该角度处的压力系数均为-0.21，压力系数在圆柱截面上下对称分布；下游圆柱的气流分离角为70 °与300 °，对应的压力系数分别为-0.20、-0.24，由于两圆柱之间间隙流的影响，压力系数在下游圆柱截面的分布是非对称的。

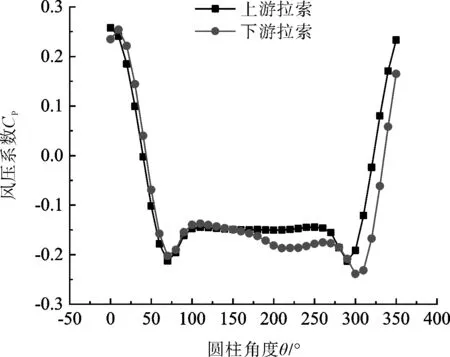
图10 α=24°平均风压系数

2.3 升、阻力系数与Strouhal数

图11到图14分别给出了α=0°与α=24°的升、阻力系数时程曲线。α=0°时力系数随时间的变化不平稳，但仍存在一定周期性特征。上游圆柱升力系数约为0，阻力系数约为0.93；下游圆柱升力系数约为0，阻力系数约为-0.24。由于上游圆柱尾流的撞击作用，下游圆柱力系数的波动幅值要大于上游圆柱。

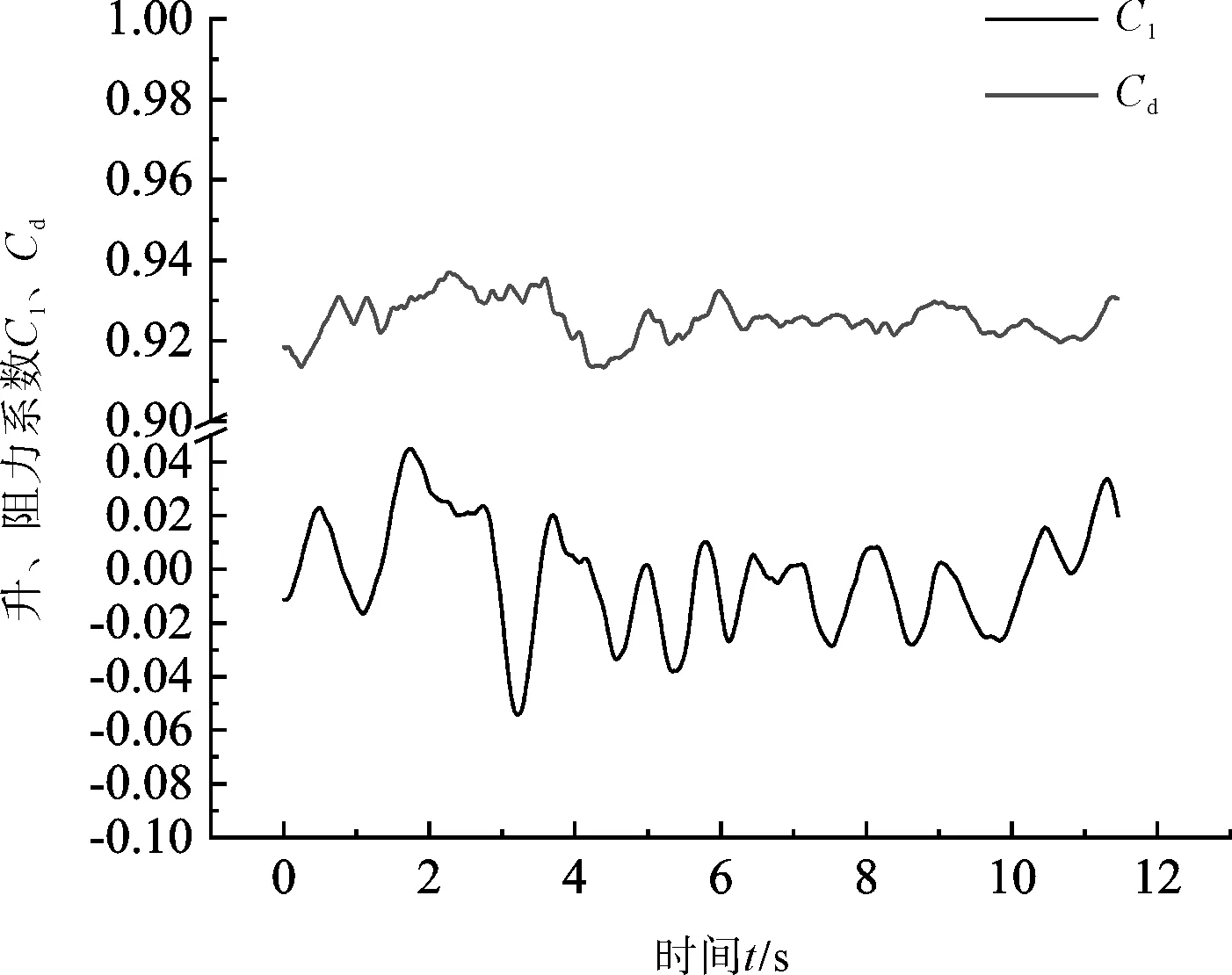
图11 α=0°上游圆柱力系数

图12 α=0°下游圆柱力系数

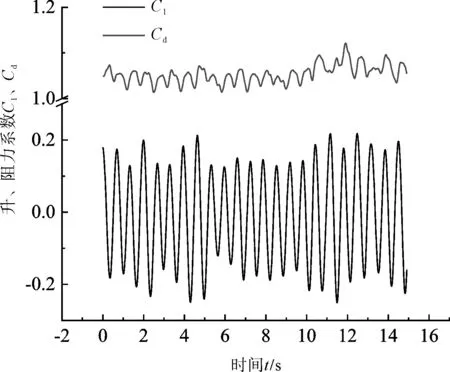
图13 α=24°上游圆柱力系数

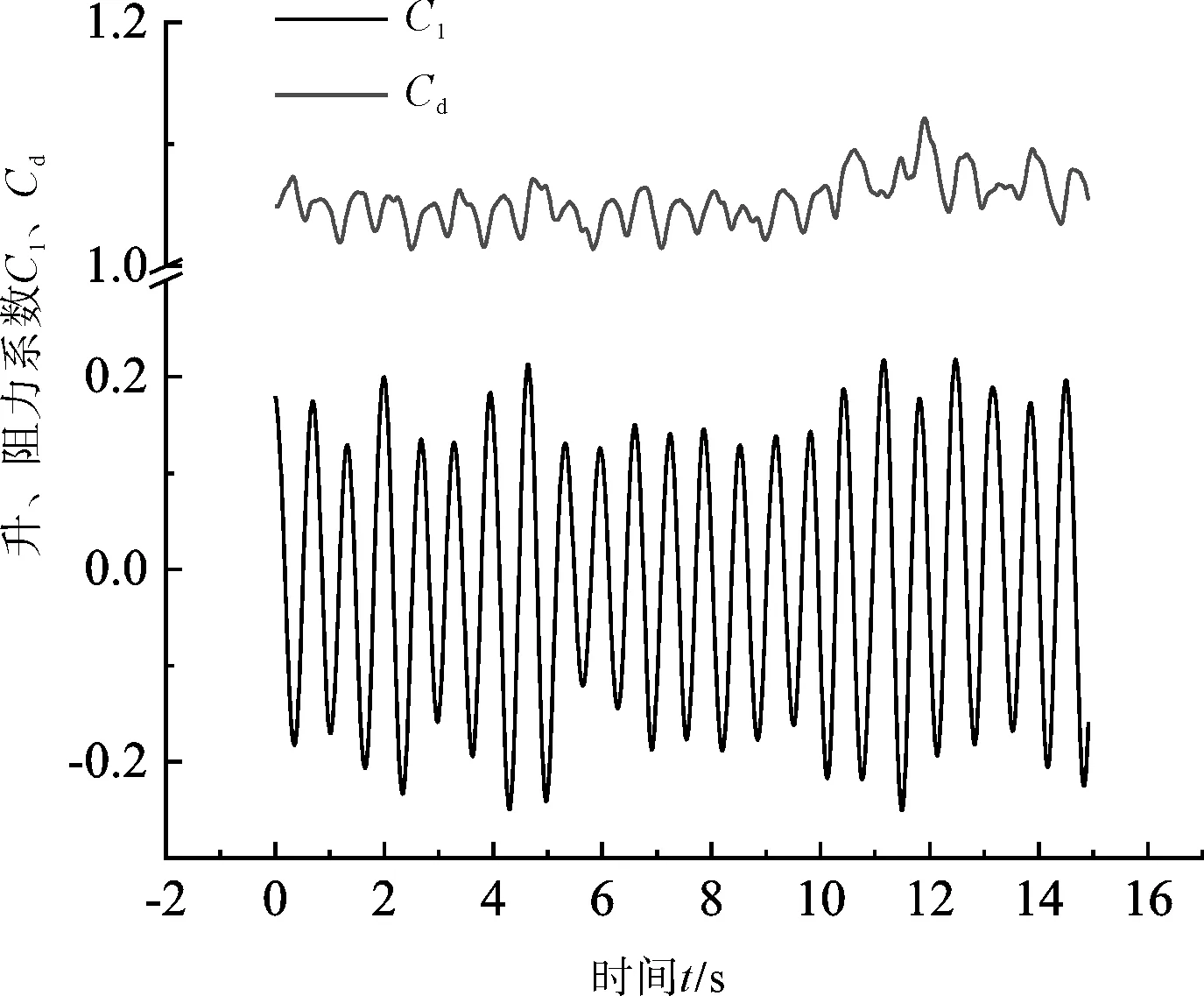
图14 α=24°下游圆柱力系数

α=24°时力系数随时间的变化具有较强的周期性。上游圆柱升力系数约为-0.02，阻力系数约为1.05；下游圆柱升力系数约为-0.38，阻力系数约为0.98。

图15展示了时均升力系数Cl与风向角α之间的关系，可以发现风向角的变化不会影响上游圆柱升力系数，其值稳定在0附近。下游圆柱的升力系数均小于零，说明下游圆柱有向上游圆柱靠近的趋势，升力系数曲线形状近似于“V”字形，风向角在8 °以下时，升力系数绝对值随着风向角的增加而增大，即下游圆柱向上游圆柱靠近的趋势愈加明显，当风向角大于8 °时，升力系数绝对值又随着风向角的增加而减小。

图15 升力系数与风向角的关系

图16展示了时均阻力系数Cd与风向角α之间的关系，上游圆柱阻力系数随着风向角的增大而缓慢增加。下游圆柱的阻力系数随着风向角的增加而明显增大，阻力系数由负值转变为正值，说明下游圆柱的运动趋势由向上游运动逐渐转变为向下游运动。

图16 阻力系数与风向角的关系

将升力系数时程进行傅里叶变换并进行无量纲化处理可以得到圆柱的Strouhal数。图17给出了Strouhal数与角度α的关系，可以发现上下游圆柱的Strouhal数始终保持一致，α=0°时Strouhal数最小，最小值为0.169，对应的涡脱频率0.963 Hz；α=6°时Strouhal数最大，最大值为0.348，对应的涡脱频率1.985 Hz。

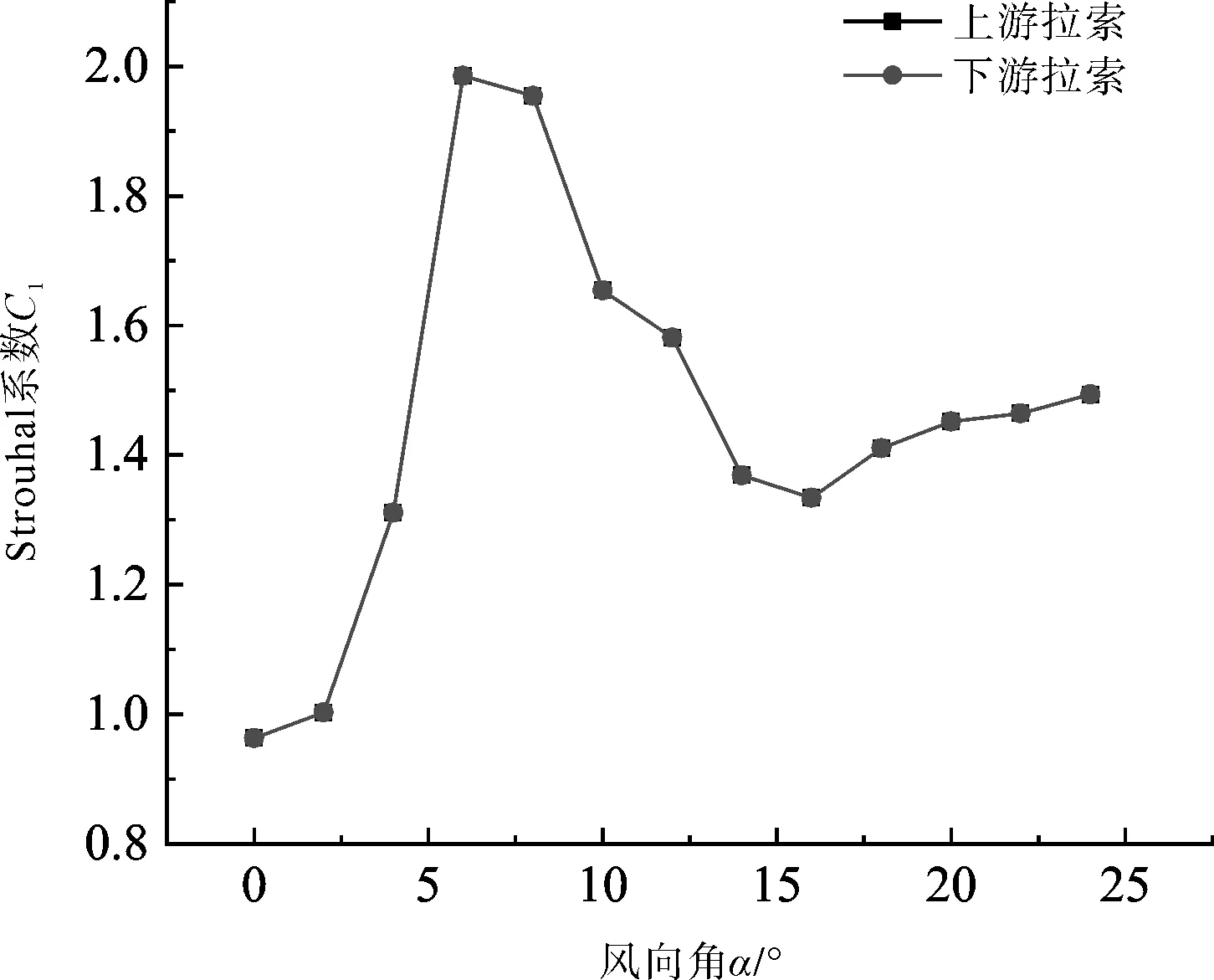
图17 St数与风向角的关系

2.4 涡脱形式

Q判据[19-20]为识别旋涡的一种方法，形式简单，并且运用广泛，所以本文以Q判据作为漩涡出现的判断准则，并给出了α=0°与α=24°时圆柱三维涡结构。当α=0°时，下游圆柱会阻碍上游尾涡的发展，导致两圆柱之间形成许多小型漩涡，并且多个方向的漩涡交错在一起使得流态十分复杂见图18；当α=24°时，上游圆柱的尾涡会绕过下游圆柱，并与下游圆柱尾涡相结合，结合后的尾流涡结构比α=0°的更宽且更加有规律性见图19，这也解释了24 °风向角比0 °风向角的的升阻力系数更具有规律性的原因。

图18 α=0°三维涡结构

图19 α=24°三维涡结构

2.5 大升力原因分析

观察图15可以发现，下游圆柱在α=8°时受到了很大的升力，为了进一步探讨下游圆柱受到很大升力的机理，选取α=8°的某个时刻来分析局部流场特性，见图20中右侧圆柱。图21为α=8°时的流线图/风速云图，图22为α=8°时的风压云图。

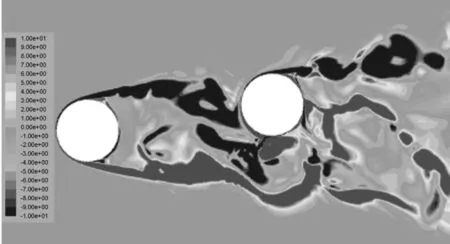
图20 α=8°涡量云图

图21 α=8°流线图/风速云图

图22 α=8°风压云图

由图21可看出，靠近下游圆柱下表面的地方，出现了高速间隙流，最大速度系数达到了1.75，对应图22中相同的地方出现了最大负压区域，该负压区域使圆柱受到较大的升力作用，这是出现较大升力的第一个原因；其次，观察图21中圆柱下表面的流线，形成了一个分离泡，说明在间隙流的影响下，圆柱下侧边界层在此分离，分离后会形成多个小型漩涡，小型漩涡与分离泡会在圆柱表面造成局部强负压，这就是导致圆柱出现较大升力的第二个原因；此外，观察图21圆柱上表面的流线，也存在边界层分离现象，在图22中对应位置出现了负压极值，分离角为79 °，根据之前的分析得知α=0 °时分离角为70 °，比较可知α=8°时负压极值点上移，导致下游圆柱会受到更大的升力作用。

以上为下游圆柱在α=8°时受到很大的升力的三个原因，并总结如下：

(1)高速间隙流引起的强负压。

(2)小型漩涡与分离泡产生的局部强负压。

(3)边界层分离点上移。

3 结论

在Re=3900的情况下采用大涡模拟的方法对中心距为3D、风向角0～24 °的错列双圆柱进行了数值模拟，研究了空气动力特性随风向角的变化，分析了大升力出现的原因。主要结论如下：

(1)随着风向角的改变，错列圆柱会出现两种绕流形态：0～8 °时，圆柱之间出现大范围的回流区域，8～24 °时，柱间回流区域转变为高速间隙流，这种转变对圆柱气动力有显著影响。

(2)随着风向角的增大，升、阻力曲线会变得更有规律性，且下游圆柱升、阻力曲线波动幅值始终大于上游圆柱，这是因为在大风向角时，上游圆柱尾涡会绕过下游圆柱并与下游圆柱尾涡相结合，形成更宽更规则的涡结构。

(3)在8 °风向时，下游圆柱升力系数会出现一个峰值，分析其原因主要有三点：一是高速间隙流引起的强负压；二是小型漩涡与分离泡产生局部强负压；三是边界层分离点由70 °上升到79 °。