灰色系统理论在悬臂拼装连续曲线梁桥施工控制中的应用

喻志刚

(西南交通大学土木工程学院，四川成都 610031)

对大跨度预应力混凝土连续梁桥来说，悬臂拼装的施工方法具有技术可行、经济合理、机械化程度高等优越性[1]。悬臂拼装法促使桥梁的施工朝着构件生产工厂化、结构装配化和施工机械化的方向发展，特别使采用节段短线匹配预制法，将成为一种较为新型的施工工艺。针对曲线连续梁桥采用此方法进行施工，更加注意控制施工预拱度以及制作预拱度。预制节段线形变化与设计基本参数、施工条件、施工方法等相关，节段几何变形可概括为纵向、水平向与竖向变形3类，这些都影响合龙的精度[2]。灰色系统理论[3]可以克服经典预测控制的不足，它的突出优点是可在“贫”信息情况下获得较好的控制效果。灰色预测方法少在三、五个数据就可以建立模型，具有实时性与实用性[4-5]。本文采用灰色预测控制法对结构的每一施工阶段形成前后进行预测，使施工沿着预定状态进行。通过预测使梁段的竖向线形和平面线形均达到预期目标，使桥梁整体控制受控。

1 灰色理论基本原理

灰色理论[5]是邓聚龙教授于1982年提出来，以关联空间为基础的分析关系，以现有信息或原始数列为基础，通过灰色过程及灰生成对原始数据进行加工与处理，建立灰微分方程为主体的模型体系，来预测系统未来的发展变化。考虑变量：

令X(0)为n元序列：

X(0)={X(0)(1),X(0)(2),…,X(0)(n)}

(1)

X(1)为X(0)的一次累加生成：

(2)

X(1)=(X(1)(1),X(1)(2),…,X(1)(n))

(3)

Z(1)为X(1)的均值生成：

Z(1)(k)=0.5X(1)(k)+0.5X(1)(K-1)

(4)

Z(1)=(Z(1)(2),Z(1)(3),…,Z(1)(n))

(5)

X(0)、X(1)为具有微分方程的内涵序列，简称灰微分序列，则X(0)、X(1)中各时刻数据满足关系：

(6)

(7)

(8)

(9)

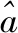
X0(k)+aZ(1)(k)=b

(10)

式中:k=2,3,…,n

上式称为GM(1，1)模型。

记残差列：

(11)

根据最小二乘法，当且仅当ε满足平方和最小原则，即:

J=εTε=min

(12)

(13)

上式的演算结果为：

(14)

(15)

灰色微分方程为：

dx(1)/dt+a⊙(X(1))=b

(16)

式(16)的参数服从式(13)，则称:

dx(1)/dt+ax(1)=b

(17)

式(17)为式(16)的白化方程或影子方程，有时也称(17)为(10)的影子方程。影子方程的解为：

dx(1)/dt+ax(1)=b

(18)

称式(18)为GM(1，1)的预测响应式，其还原值为：

(19)

灰色系统理论将多跨连续梁桥的施工标高预测视为一个灰色系统。在第i+1号梁段施工前，通过计算得到已浇梁段在理想状态下的挠度变化值，在第i节段施工完成后，测得前i节段挠度变化实测值，对两者建立误差序列，以此为原始序列，建立GM(1，1)模型。在各阶段预留拱度理论计算状态序列:

X=(X(1),X(2),…,X(n))

对应X有实测值序列：

Y=(Y(1),Y(2),…,Y(n))

根据X、Y建立误差序列：

δ=(δ(1),δ(2),…,δ(n))

元素

δ(k)=X(k)-Y(k)+c

(20)

k=1,2,…,n

式中：c为非负化常数，其值等于X(i)-Y(i)的负数中绝对值最大者。

下阶段立模时的预留拱度：

U0(k)=X(k)+δr(k)

(21)

式中：X(k)为原定理想状态在K阶段初的预留拱度计算值。

2 工程概况

苏通长江大桥北引桥B2标(图1)上部结构为双幅预应力混凝土等高度连续箱梁，拼装的首联下游幅桥跨组合为50 m+9×75 m预应力混凝土等高度连续箱梁，梁高4 m，单箱单室，在墩顶设3 m厚中横梁，梁端设端横梁，其余部分均不设横隔梁。箱梁顶板宽16.4 m，底板宽6.5 m；腹板厚度从90 cm变化到40 cm；顶底板厚度均为25 cm；悬臂长度3.95 m(图2)。

图1 苏通长江大桥示意

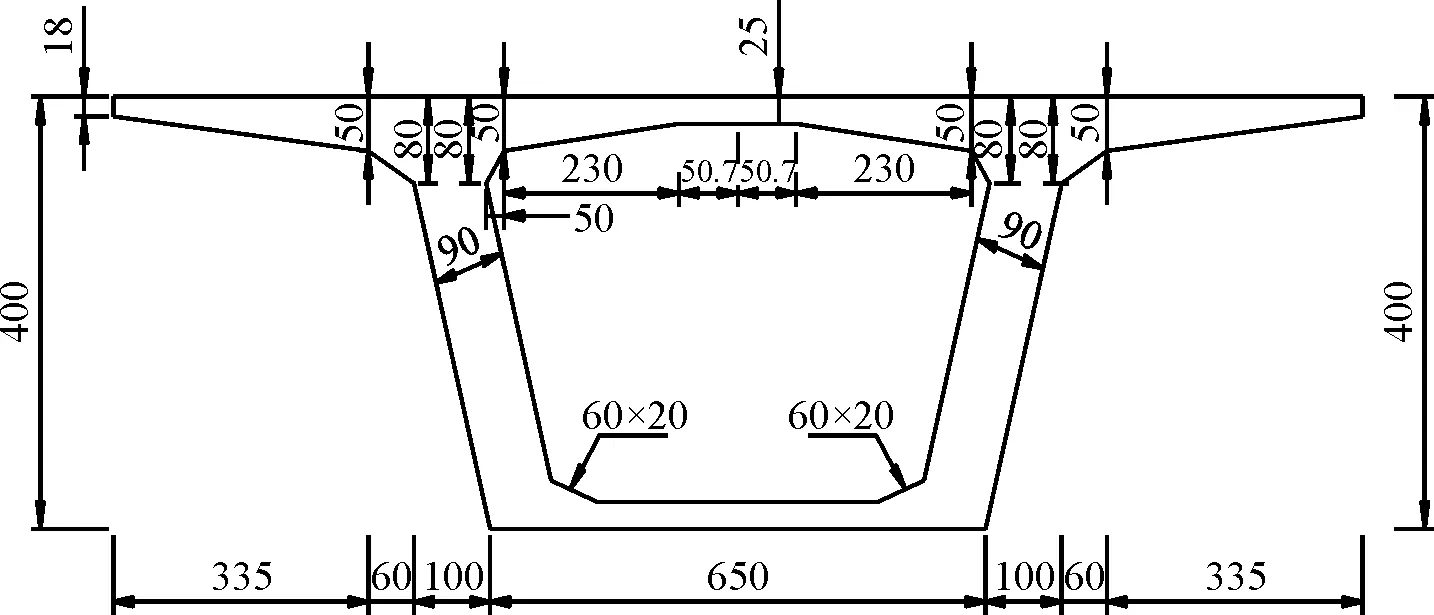
图2 箱梁标准断面(单位：cm)

3 模拟计算分析

采用建立在薄壁曲线箱梁理论之上的箱梁有限元法。每个单元有i和j两个节点(截面)，对于曲线箱形截面梁，由于弯曲、拉压、扭转、畸变和翘曲各种变形全部耦合，而不能将其中的某一因素单独求解，所以必须考虑全部9个自由度。梁和墩之间的联结根据实际约束条件采用主从关系来处理；在梁段悬臂拼装时，首先应锁定墩顶支座，使其暂时成为固定支座，中跨墩采用钢绞线束进行墩梁临时固结措施，以抵抗施工过程中出现的不平衡弯距。墩在承台处进行固接，约束墩各个方向的位移。二期恒载按65 kN/m，作为均布质量分配到混凝土梁单元中。最后得到混凝土连续梁的分析模型共有327个单元，339个节点，分为146个施工工况进行模拟施工计算。模型图见图3。

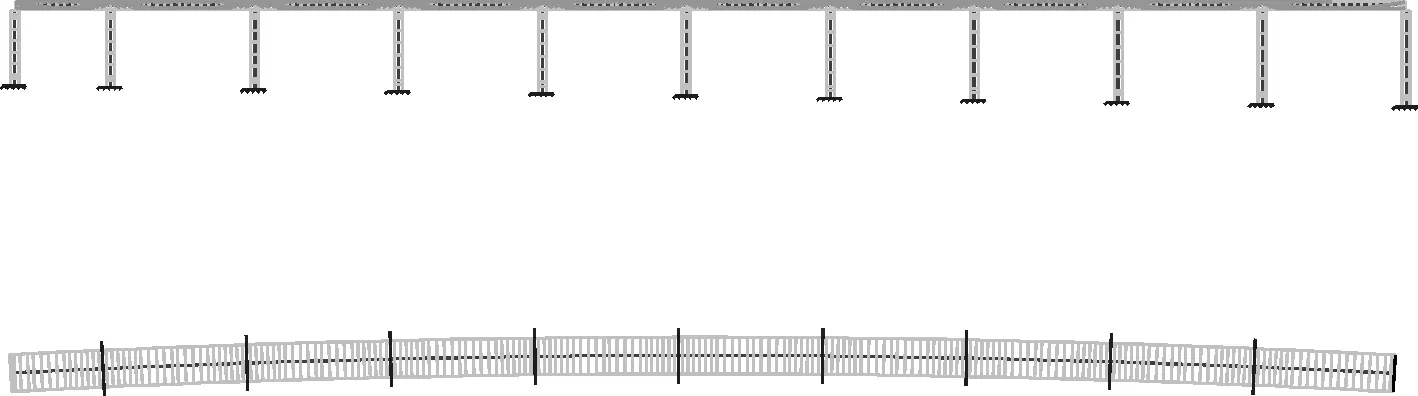
图3 模拟计算模型

本文将以苏通长江大桥B2标曲线连续梁桥为实例说明预拱度的确立，通过预拱度可以得到梁段的制作线形，从而精确地为梁段的预制提供局部坐标。利用全桥模拟结构分析，计算出各点的总位移，将其反向成为制作预拱度，以47#墩悬臂拼装为例，如图4所示。

图4 47#墩最到悬臂状态结构

以47#墩的梁段预制为例，说明通过控制各预制节段匹配位的空间位置，从而达到节段拼装后梁体的线形，以满足设计线形的要求。通过的梁段控制点的坐标和预拱度的考虑，结合理论值与梁段在匹配生产时的测量值，经过必要的误差修正，精确的计算出已成梁段在匹配位置时应处的空间位置。以47#墩南侧施工为例，由计算得出总预拱度，如图5所示。

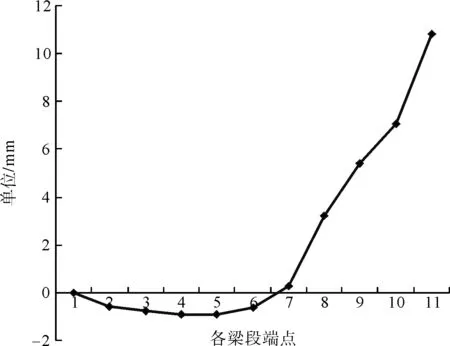
图5 47#墩南侧制作预拱度

短线匹配法节段预制工艺原理就是指将箱梁分成若干短节段，考虑混凝土收缩、徐变、预拱度等影响因素，将每榀梁段的成桥整体坐标转换为预制厂局部坐标，以待浇梁段为基准，调整已制前相邻匹配梁段平面位置及标高，在预制台座的固定模板系统内逐榀匹配、流水预制梁段。

4 曲线连续梁桥结构状态的参数分析

4.1 梁段自重误差分析

梁段自重误差主要来源于混凝土的容重误差和梁段成型尺寸误差。这些误差带有随机性，呈偏态分布，即有系统偏差的成分。至于梁段成型尺寸，这与预制模板刚度有关，常有尺寸超过设计值的情况，根据多座桥的经验，梁段的自重普遍超过设计值，其超出的幅度以5 %左右较为常见。

苏通长江大桥考虑了箱梁自重的不均匀性，对“T”构进行施工工况的验算，一侧悬臂自重增加4%，另一侧悬臂自重减少4 %。下面以47#单“T”悬臂施工为例，选择江面北侧增加4 %的自重，江面南侧减少4 %的自重。计算得出各控制点挠度影响见图6。

图6 梁段自重误差对比

由以上可以看出，自重在47#墩的悬臂江面北侧增加自重4 %，江面南侧减少自重4 %后，自重引起的变化值比较大，梁段悬臂越长，影响越大，所以在梁段预制时，要控制好梁段的重量。

4.2 弹性模量的分析

混凝土梁的弹性模量值E往往比规范建议的取值要高，这一方面与施工现场混凝土实际弹性模量往往偏高有关，另一方面也与值偏低有关。本文取弹性模量偏高10 %为例(图7)。

图7 弹性模量误差对比

通过对弹性模量的分析，弹性模量的变化，对主梁的挠度和弯矩影响都很小，在进行误差调整时可以忽略不考虑。

4.3 临时荷载误差分析

临时的施工荷载包括材料、机具的堆放对梁的挠度和弯矩也是产生误差的一个方面，本文对“T”构进行施工阶段分析，悬臂端按照200 kN集中力分析。

由图8可以看出临时荷载对各点的挠度变化值影响比较大，同时对弯矩的影响也较大，使桥墩也产生了弯矩，所以在误差分析时不可忽略，要主要考虑。

图8 临时荷载误差对比

4.4 预应力误差分析

在施工过程中，由于施工人员对预应力的张拉可能造成误差，所以预应力的误差对梁段的挠度、弯矩也能造成影响(图9)。

图9 预应力误差对比

由图9可以看出预应力的变化对各点挠度的影响也比较大，在施工中能引起一定的误差，所以在施工中一定要控制好预应力的张拉，以免因预应力的原因造成较大的挠度，弯矩的变化。

5 灰色模型预测分析

由于预测状态与实际状态免不了有误差存在，某种误差对施工目标的影响则在后续施工状态的预测予以考虑，以此循环，直到施工完成和获得与设计相符合的结构状态。悬臂施工的预应力混凝土连续梁桥其已成节段的状态(内力、标高)是无法调整的，只能对待施工的节段预测状态进行改变。以47#墩南侧预制梁9号块的计算为例，说明灰色理论在悬臂拼装中的应用。

在8#块施工周期中，4～8#块的挠度变化理论计算值为：

x=(-1,-2,-2,-3,-2)

实测值为：y=(-5,-7,-3,-1,1)

则得到误差序列：

X=(4,5,-1,-2,-3)

取c=3对误差序列进行非负化，得到新的误差序列：

X(0)=(7,8,2,1,0)

作一次累加生成累加生成序列：

X(1)=(7,15,17,18,18)

建立数据矩阵，求解得出

a=1.1202

b=20.2525

建立模型：

dx(1)/dt+a⊙(X(1))=b

即：

残差修正，由：

得到残差序列为：

(0.5349，0.0996，0.3052，0.046)

对残差序列建立残差GM(1，1)模型。

预留拱度为：U9=x9+2.8023

由于施工控制过程中涉及的数据很多，手算工作效率低，而且极易出错。可通过编制程序计算，表1列出47#墩右侧梁段预测调整值。

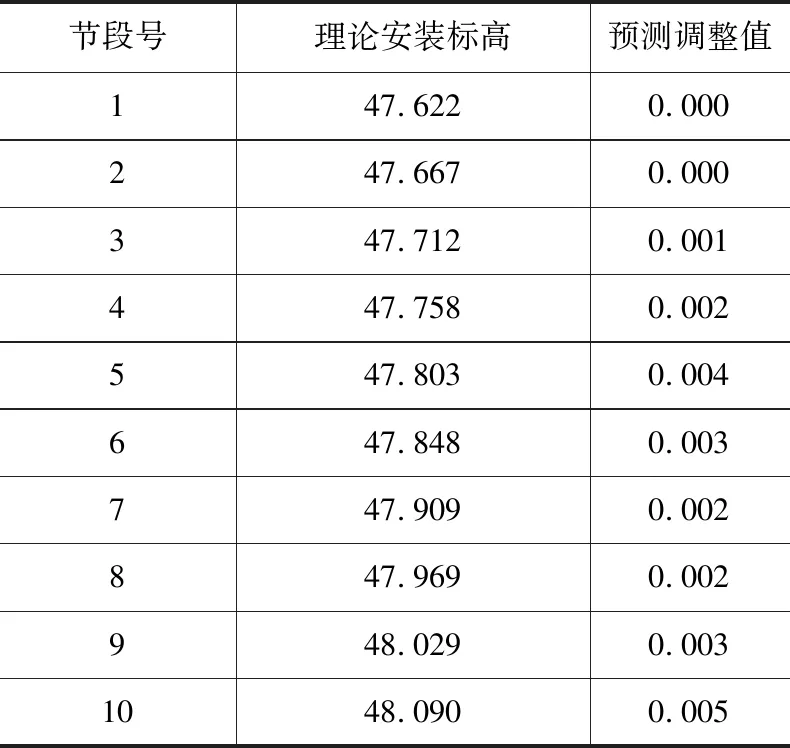
表1 47#墩南侧梁段预测调整值

6 实桥线形控制结果

从施工结果可以看出，施工控制过程比较合理，悬臂的竖向线形与原设计比较接近，可见灰色预测控制系统能够用于悬臂拼装连续梁的施工控制，并且能取得较好的控制结果。

由于采用短线匹配法对梁段进行的预制，也对平面安装的理论坐标与安装后的实际坐标进行比较，以验证短线匹配法在悬臂拼装中的运用，47#墩南侧左幅悬臂拼装平面X、Y坐标控制结果

从施工结果可以看出，运用短线匹配法预制的梁段在拼装后的平面线形基本完全与理论线形吻合，特别是纵向上吻合的很好(图10～图12)。这说明在预制时对在平面产生的误差，能够及时地调整，保证了平面线形，为顺利合龙保证了精度与质量。

图10 47#墩南侧左幅控制曲线

图11 平面X坐标控制线形

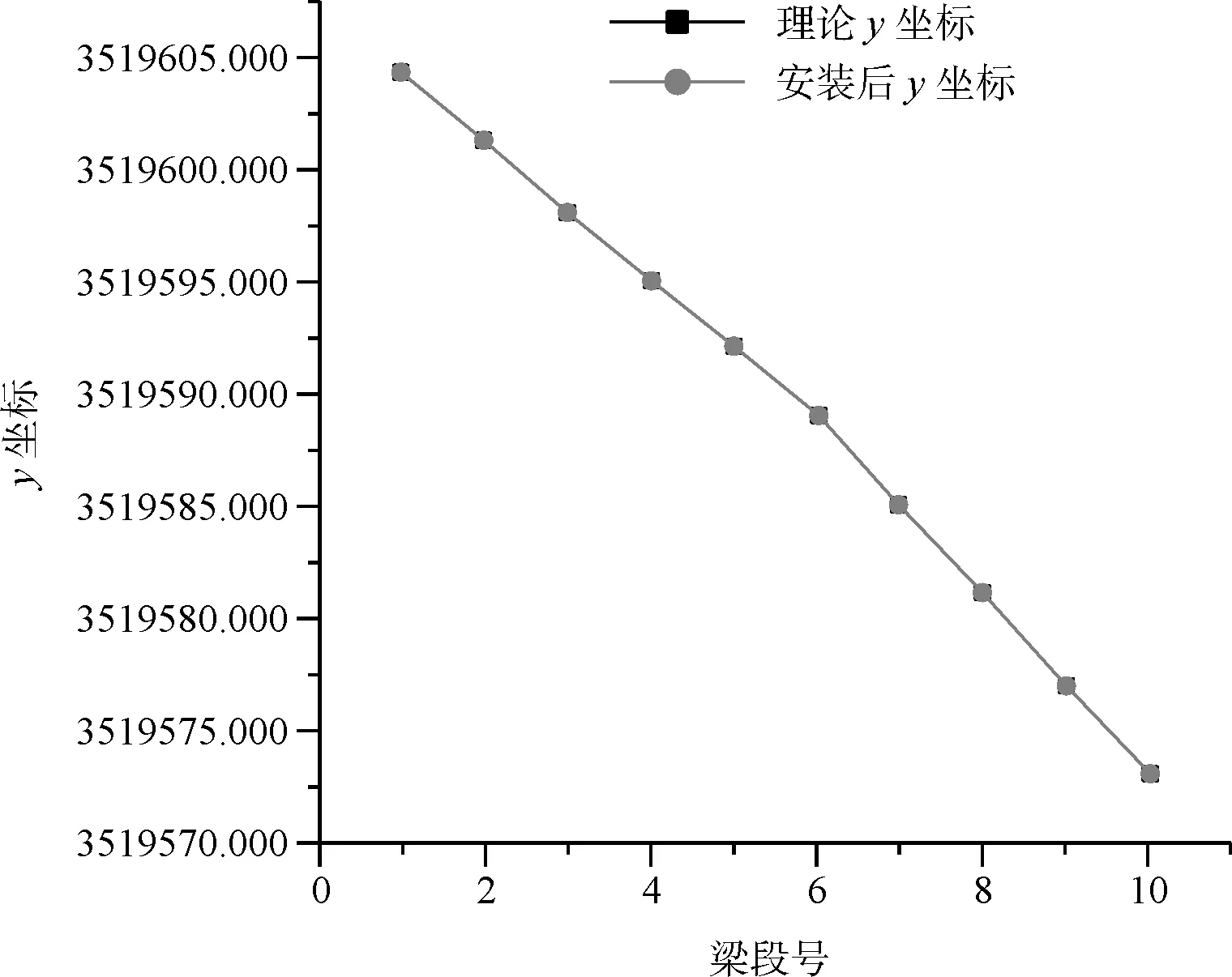
图12 平面Y坐标控制线形

7 结论

通过对参数分析，可以看出梁段自重、临时荷载、预应力等对桥梁变形影响较大，所以在施工控制中要考虑。

预测控制的模型采用灰色模型GM(1，1)，它能够通过很少的数据建立，并且能够实现数据的新陈代谢，故预测控制是实时的，此外预测控制是“采样瞬态建模”控制，每采集一个新数据，就建立一个新模型，随之更新一组模型参数，实质上是用模型参数的不断更新，来适应行为的不断变化、环境的干扰和噪音的影响，所以灰色预测控制具有较强的适应性。

通过苏通大桥北引桥B2标的施工控制表明，灰色预测控制系统不仅可以对多跨连续梁桥的施工进行控制，而且方法简单、效果可靠。