考虑水位频动影响的周宁坝址区边坡运行期稳定性分析

黄文洪，张 健，李龙龙，朱永生，潘 兵

(1.华电福新周宁抽水蓄能有限公司,福建宁德 352100；2.浙江中科依泰斯卡岩石工程研发有限公司，浙江杭州 311122；3.中国电建集团华东勘测设计研究院有限公司，浙江杭州 311122)

当水电站进入运行期后，边坡岩体因库水位变化将经历极为复杂的应力-渗流耦合作用过程。水介质流动在降低岩体有效应力的同时，还可能以参与物理化学作用的方式改造岩体物质结构、影响岩体强度条件，综合导致边坡岩体稳定性水平降低，给边坡、水工结构及工程影响区带来潜在安全问题。

水作用对边坡稳定性的影响是工程设计需要重点考察的内容之一，试验测试与数值分析是目前针对该类型问题研究采用的较为普遍的基本解决手段。李邵军等[1]依据三峡库区典型滑坡的工程地质特征，采用离心机模型试验研究了库区边坡在水位升降作用下的失稳过程。贾官伟等[2]利用大型模型试验研究了水位骤降引致邻水边坡滑坡的原因及失稳模式。文献[3]～[5]采用连续介质或非连续介质力学方法考察了不同类型岸坡岩体在水库升降变化条件下的渗流特征及分布变化规律、水岩相互作用，分析了边坡孔隙水压力变化特征和渗流速度动态变化规律,为进一步开展渗流与变形耦合分析提供了依据。目前考察水作用条件下的边坡稳定性分析方法主要包括非耦合方法和耦合方法两类，前者如文献[6]～[11]将库水位变化过程简化为一系列不同的水位线，借助极限平衡方法分析了边坡在水位变化过程中的稳定性条件以及演变规律，并讨论了渗透系数、水位升降速率等关键参数的影响，文献[12]进一步考虑了水渗透作用对岩体力学参数及其稳定性的影响；与此不同地，文献[13]～[15]则采用基于Geo-Slope等软件或方法具有的流固耦合分析功能对水位变化条件下的边坡稳定性及参数影响规律进行了深入研究。

对抽水蓄能电站运行期边坡稳定性分析而言，水位变化并非单调抬升或降低，需考察周期性水位频动(在死水位与正常蓄水位之间周期性变化)条件的影响，不考虑应力与渗流动态相互作用过程的非耦合方法显然无法满足稳定性分析的要求。以福建周宁抽水蓄能电站下水库作为研究对象，为兼顾分析效率和研究目的为原则，选择基于连续介质渗流理论的FLAC3D程序并采用其应力-渗流耦合功能分析预测库岸边坡岩体在运行期水位频动条件下的稳定性特征，为类似工程问题摸索研究方法基础，同时为周宁电站运行期工程设计提供决策依据。

1 工程概况

福建周宁抽水蓄能电站位于福建省宁德市周宁县境内，距宁德市、福州市的直线距离分别为50 km、110 km，距周宁县城约20 km。电站下水库位于七步溪河谷上，为山区峡谷型水库，水库库周群山环抱，山体雄厚，无低邻谷和低于正常蓄水位的垭口，库区总体为长条形峡谷。下水库大坝为碾压混凝土重力坝，坝顶高程306 m，最大坝高108 m，坝顶长度216.50 m，坝顶宽度9 m。下水库正常蓄水位299 m，死水位262 m。见图1，枢纽主要由上水库、下水库、输水系统、地下厂房及开关站等建筑物组成，电站设计装机容量为1 200 MW[17]。

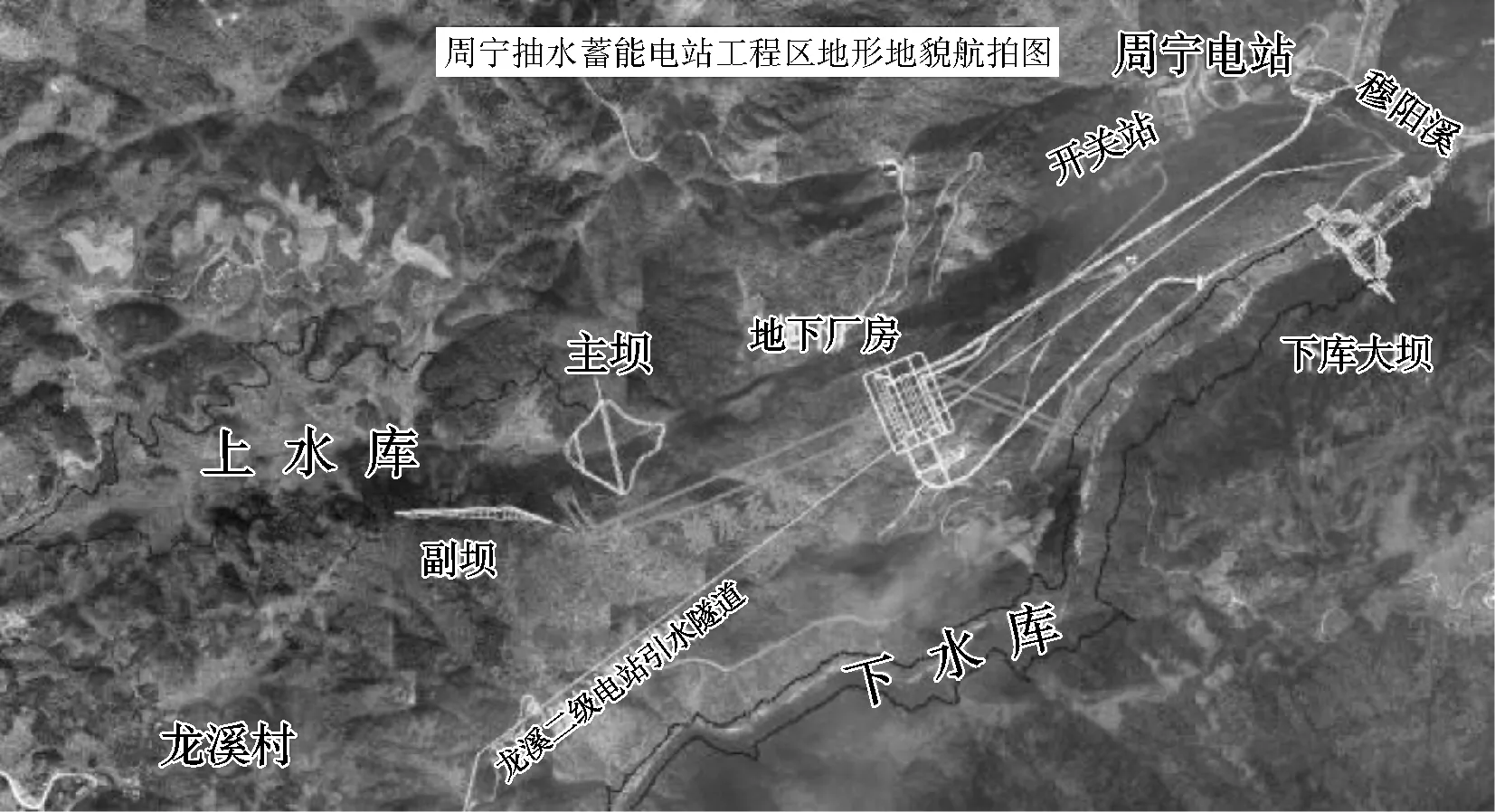
图1 周宁抽水蓄能电站地形地貌及主要建筑物布置

库区为强烈切割中低山陡坡地貌，河谷呈深切的“V”字型，库周山体高耸，地表分水岭雄厚。河床高程在209～302 m之间，正常蓄水位高程以下两岸岸坡地形陡峻，坡度一般在38～60 °。地勘揭露下水库(坝)区出露基岩地层主要为中生界侏罗系上统南园组地层，燕山晚期侵入岩及地表第四系地层；岩性以钾长花岗岩为主，岩石由钾长石、斜长石、石英和黑云母等矿物组成，呈中细粒花岗结构、块状构造。库区两岸多为强～弱风化基岩出露，全风化层厚度不大，发育有多条辉绿岩脉(βμ)及一条石英二长斑岩脉(ηoπ)。

2 分析原理及模型条件

2.1 应力-渗流耦合分析原理

基于连续介质力学方法的FLAC3D程序在考虑岩土体流固耦合效应时，将岩土体视为等效连续的孔隙介质，采用经典Darcy定律描述流体介质在其中的流动过程，并同时满足Biot方程，即认为岩土体骨架及矿物颗粒为可压缩物质。流体渗流及其与应力的耦合作用满足如下主要控制性方程[16]。

2.1.1 流体运动方程

流体运动用Darcy定律来描述，对于均质、各向同性固体和常密度流体的情况，Darcy定律的等效形式为：

qi=-k(p-ρwxjgj),i

(1)

式中:qi为单位截面流体流量m3/s，k、(p-ρwxjgj),i分别表示孔隙介质的渗透系数m2/(Pa·s-1)和水力梯度，其中，p为孔隙水压力Pa。

2.1.2 平衡方程

对于不考虑固体介质即岩土体变形的理想情形，流体介质平衡方程满足下式定义：

(2)

式中:qv为单位体积岩土体中的流体补给量，ζ为单位体积孔隙介质的流体体积变化量即不平衡量。当进一步考虑应力-耦合作用过程中岩土体骨架、矿物颗粒可以发生的压缩变形及其可能的温度作用响应时，以单位体积非饱和孔隙介质作为考察对象，其平衡方程最终表现为如下形式：

(3)

式中:M、α分别为Biot模量N/m2和比奥系数(无量纲，在0～1之间取值)；K、Kf分别为固体骨架与流体的体积模量N/m2；n、s分别表示孔隙介质的孔隙率和饱和度；ε为固体骨架体积应变；T、β分别为温度℃和考虑流体和固体颗粒的热膨胀系数℃-1。

2.1.3 孔隙介质运动方程

孔隙介质运动采用牛顿第二定律进行描述：

(4)

式中:ρ为孔隙介质密度(kg/m3)，且ρ=ρd+nsρw，其中，ρd、ρw分别为固体密度和流体密度；vi为介质运动的速度的三个分量m/s。

2.1.4 本构方程

固体骨架及其矿物颗粒体积改变可引致流体孔隙压力的变化，孔隙压力变化反过来也会导致前者改变，从而影响岩土体应力状态。孔隙介质本构方程的增量形式为：

(5)

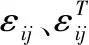
2.2 分析模型构建

图2为分析采用的三维岩体应力-渗流耦合分析模型，其中对不同地质单元进行了区别化着色处理、以便考察模型范围内的地质条件。为求得分析精度与求解效率之间的合理平衡，经调试确定数值单元的最小边长为4.0 m，模型共计含有数值单元约35×104个。

图2 应力-渗流耦合稳定性分析FLAC3D数值模型

依据基本地质条件的丰富程度和有效性，模型沿顺河和横河向分别考察了约650 m×600 m的分析范围。鉴于主要地质构造发育特点，采用有厚度单元进行模拟断层与岩脉构造，图3给出了主要地质构造和坝工结构的空间关系。其中，断层F3考虑了影响带(影响带宽度1.0～2.2 m)；重点描述了辉绿岩脉βμ3、βμ6和石英二长斑等主要岩脉；依据坝基防渗设计要求，模型还特别表征了灌浆帷幕。在模型设置环节，将灌浆帷幕和坝体处理为不透水材料。鉴于灌浆范围及其力学特性的不确定性，保守考虑其力学参数与所在部位岩体一致。

图3 主要地质构造及坝工结构

进一步考察图2、图3可见，坝址区及上下游库岸基本地质条件具有特征：

(1) 上游库区边坡表层岩体以弱风化为主，全风化及强风化地层仅在右岸边坡蓄水位高程以上局部揭露。

(2) 断层F3陡倾交切于左岸坝址区边坡，受坝体压坡作用影响，运行期断层F3对坝肩边坡的变形影响可能得到有效抑制。

(3) 辉绿岩脉βμ6在库岸上游主要在底高程河谷一带揭露，其影响也可以因河谷高应力区作用得到一定程度抑制；除βμ6外，二长斑岩脉主要揭露于在右岸较高高程一带，且朝向边坡外侧山体厚度较厚、承载力高。经验地，以上基本地质条件揭示，尽管模型范围内构造发育，但由其发育特点及工程结构压坡作用决定的，构造对岸坡变形稳定性的不利影响或许不突出，后续分析结果对这一认识进行了验证。

2.3 岩体力学参数取值

结合工程区不同岩性及重点地质构造内充填物的结构特征、强度、风化程度、卸荷特性、完整性指标和结构面性状等因素，对岩体进行了工程地质分类，并给出了各类岩体物理力学参数建议取值，参见表1。岩体本构模型采用摩尔库伦弹塑性本构模型，该准则是传统Mohr-Coulomb剪切屈服准则与拉伸屈服准则相结合的复合屈服准则。

表1 岩体物理力学参数取值

在目前工程实践中，由于岩体失稳通常主要表现为剪切破坏，岩体抗剪特性受到广泛关注，往往忽略了对抗拉强度条件的研究，现有勘察规范就未对岩体抗拉强度明确建议取值。运行期库岸水力坡降在水位降低过程中指向坡外，渗透力也因此指向边坡外侧，使得岩体具有受拉应力作用的荷载条件，岩体抗拉强度也应是变形稳定性分析模型需描述的条件之一。现阶段尚未取得周宁抽蓄电站岩体抗拉强度相关试验成果或建议取值依据，分析中采用经验方法来确定岩体的抗拉强度即取单轴抗压强度一定比例值作为抗拉强度，比例系数经验取值区间为1/5～1/20。其中，岩体单轴抗压强度定义为：

(6)

式中，Nφ=(1+sinφ)/(1-sinφ)，c、φ分别为岩体的粘聚力与内摩擦角。本次分析按保守考虑取比例系数为1/15。

透水试验表明，工程区岩体透水性随风化程度降低而减弱，以弱—微透水性为主，表2给出了依据试验成果及其经验认识确定的岩体水动力参数取值结果。分别采用各向异性及其正交各向异性水力学模型模拟岩体和地质构造的渗透特性。岩体渗透系数张量K由左右岸裂隙构造条件确定，并经透水试验各向同性渗透系数进行修正；对地质构造而言，表中数值给出的是其构造面内的渗透系数，倾向方向渗透系数取值按表中数值的1/10考虑。

3 运行期库岸边坡稳定性分析

在开展运行期应力-渗流稳定性分析之前，要求建立起始模型状态。该状态的应力条件是区域初始地应力、坝工结构浇筑和初始地下水应力等因素的叠加作用结果。以图2模型为分析条件，通过必要的模型设置、采用非耦合方法依次开展初始地应力分析(考虑天然水位与初始地应力)、坝体浇筑分析及初期蓄水分析(水位自天然水位至死水位262m)得到运行期应力-渗流耦合分析所需的模型条件。

表2 岩体水动力学参数取值

依据运行期水位变化规律，可视一个自然日为一个运行(水位升降)周期，并结合非完全耦合分析方法特点将运行周期分解为五个关键性时间节点，即①初期水位(死水位262 m)→②正常蓄水位(299 m)不排水分析→③正常蓄水位排水分析→④死水位不排水分析→⑤死水位排水分析，其中，①→③、③→⑤分别对应于6、18个自然小时。①为针对一个运行周期开展应力-渗流耦合分析应依据的初始状态；据此将水位抬升至正常蓄水位，依据库水渗透远滞后于应力传播这一基本力学特点，采用不排水方法得到库岸岸坡岩体的变形、应力及其水压力响应条件，该过程对应于时间节点②；在水位上升过程中，库水入渗实际必然伴随岸坡蓄水响应过程，节点③即为基于排水分析方法获得库水入渗对岸坡地下水压力调整，及其对岩体变形稳定性影响的结果；在发电阶段及后期，库水位自正常蓄水位降至死水位，针对该过程采用的岸坡力学与流体响应分析原理与②、③一致，即分别基于不同排水条件获得对应于节点④、⑤的分析结果。

图4给出库岸边坡坡表岩体横河向、顺河向变形及其总变形在发电运行75 d后的分布状态，以考察岸坡基本变形特点与因此指示的稳定性条件。其中，横河向、顺河向变形用于指示变形方向，而总变形主要用来反映变形水平。图中同时标识了若干变形测点的分布位置。

图4 运行完成75 d后，岸坡岩体变形分布特征

由计算结果可见，在75个(d)发电周期运行完成后，横河向、顺河向及其总变形均处于不足1mm的低水平，变形相对突出部位主要分布在强风化岩体内，横河向与顺河向变形水平相对关系及方向进一步指示岸坡岩体变形方向总体指向边坡内侧，且未揭示主要断层与岩脉地质构造对变形可能产生明显的不利影响。这些变形特点可以说明，在给定的运行时间内，岸坡受水位周期性变动引致的变形基本指向坡内、且变形水平不高，意味着岸坡稳定性受影响程度不大，可以维持较好的稳定性条件。

图5、图6依次给出了左、右岸边坡典型测点(参见图4测点分布)部位岩体总变形在75 d运行期内的演变过程曲线，以进一步考察曲线形态特别是收敛特性可以揭示出的岸坡岩体变形特点和稳定性条件：

图5 岸坡左岸典型测点总变形在运行期间(75 d)的演变过程

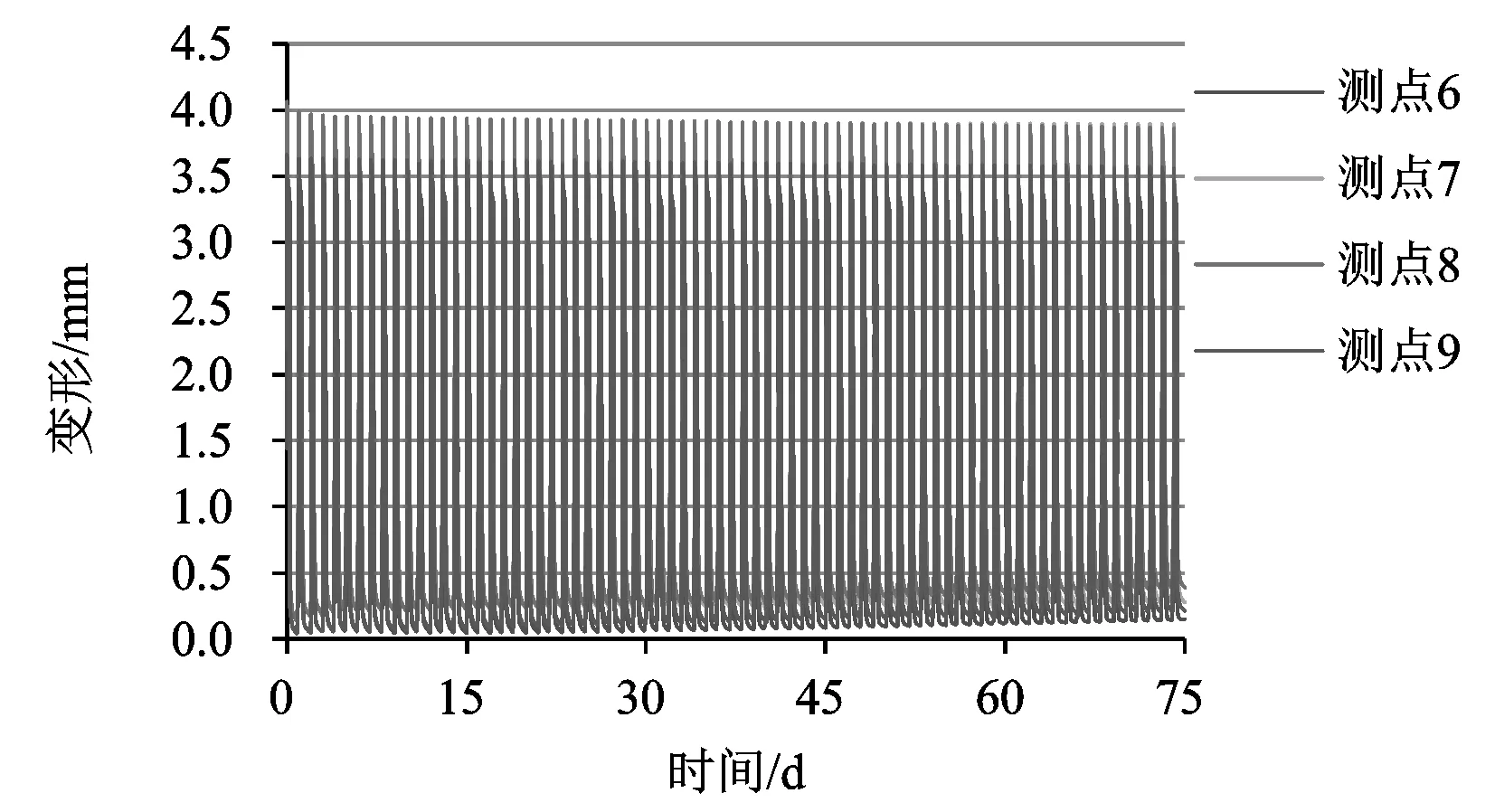
图6 岸坡右岸典型测点总变形在运行期间(75 d)的演变过程

(1)测点5、测点8处岩体是左、右岸边坡在运行期变形相对显著的部位，最大变形分别不超过3 mm和4 mm。

(2) 考察测点变形曲线形态特点可见，库岸边坡变形响应规律在给定的75 d运行时间内均可以达到收敛状态，指示岩体能够满足自稳要求。

(3)综合上述分析可见，左右岸岸坡岩体在运行过程中可以维持较好的稳定性条件。

图7、图8给出了测点部位岩体横河向变形在75 d运行期内的演变过程曲线，其特点进一步验证了测点部位岩体在运行期因水位变动诱发的横河向变形总体指向坡内的认识。在水位上升期间的，库水作为坡表荷载引致边坡发生压缩变形，这部分变形在水位降低期间则由于库水荷载释放形成的回弹变形而抵消，边坡总变形最终处于不超过1 mm的低水平。

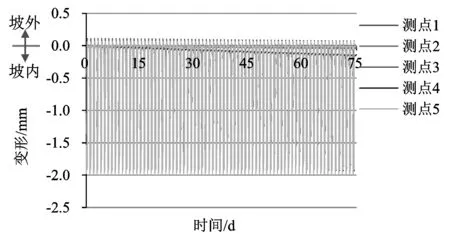
图7 岸坡左岸典型测点横河向变形在运行期间(75 d)的演变过程

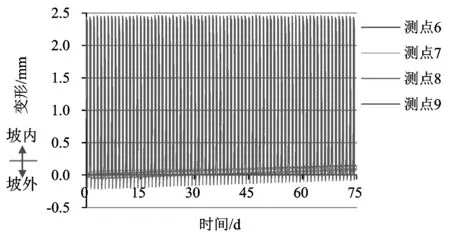
图8 岸坡右岸典型测点横河向变形在运行期间(75 d)的演变过程

针对施工期的强度折减法稳定性分析表明，在不考虑坝体浇筑对边坡的压坡作用的前提下，岸坡安全系数不低于1.6，满足规范对其开挖阶段的稳定性要求。前述运行期应力-耦合分析成果揭示，水位频动条件对岸坡变形影响不明显，耦合作用引致的岸坡总变形不足4 mm，岸坡耦合总变形达到收敛时也不超过1 mm，且变形方向总体指向边坡内侧，这些变形特点均指示岸坡岩体在运行期可以维持原有的稳定性条件。由此可以推断，岸坡可满足运行期稳定性要求，且安全系数可达1.6左右的较高水平。

4 结论

(1)对抽水蓄能电站而言，岸坡在运行期的稳定性分析应合理描述因库水位频动变化影响将经历的复杂的应力-渗流耦合作用过程。

(2) 在水位降低过程中，指向坡外的渗透力可使得岩体承受拉应力作用，此时岩体抗拉强度应得到合理描述。

(3)周宁抽水蓄能电站在运行期间，因水位频动引致的岸坡变形总体不超过4 mm，最终收敛变形也处在不足1 mm的低水平，且变形总体指向边坡内侧，变形特点有利于边坡稳定性条件得以维持。

(4)周宁抽水蓄能电站库岸边坡可满足运行期稳定性要求，且安全系数可达约为1.6的较高水平。