事件与变量间相依性分析及其应用
2020-09-17杨语蒙李兴东王善培
杨语蒙 李兴东 王善培
(兰州交通大学数理学院 甘肃 兰州 730070)
引言
传统意义下的相关关系就是线性相依关系,但随机数据或随机变量间往往存在更为复杂的非线性相依关系,因此对随机数据或随机变量进行相依性分析具有更重要的应用价值.目前为止,相依性分析广泛应用于股票市场的随机波动、银行贷款、医疗诊断分析等领域.在早期的研究中,陈睿君首次提出了相依违约的违约风险度量[1];张金清,李徐等人运用连接函数研究流动性风险与市场风险[2].后期也有很多学者对变量间的相依性分析进行研究,主要借助Sklar定理进行探讨[3][4],如张尧庭借助Copula函数刻画股市间的相依性[5];韩思远基于熵对相依程度度量[6];张亚文基于相对距离研究变量间的相依性[7].笔者认为,条件概率是相依性分析的概率基础与重要工具,克服了前面度量指标的局限性.目前相关研究较少,该文基于条件概率、条件分布、条件期望等不同角度探讨事件、随机变量间的相依性,并阐述相依性分析的应用实例,以抛砖引玉.
一、从不同的角度刻画事件之间的相依性
(一)借助条件概率刻画事件之间的相依性关系
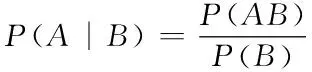

由条件概率公式,进一步得到:事件A与事件B正相依,当且仅当P(AB)>P(A)P(B);事件A与事件B负相依,当且仅当P(AB) (二)借助贝叶斯公式刻画事件之间的相依性关系 (三)借助似然度刻画任意随机事件之间的相依性关系 定义2.设A,B是任意两事件,则称λ(A,B)为A与B的似然度.特别的,若P(A)与P(B)中至少有一个为0,则规定λ(A,B)=1. 可见,任意两事件A与B的似然度λ,实质是集合A与B的二元集函数,且函数值是非负实数.无论似然度λ取任何非负值,A与B彼此间的作用是相互的、同向的,且作用程度是等量的,任何一个后验概率都等于对应先验概率的λ倍,这就是任意两事件间的相依原理. 至此,分别从条件概率、乘法公式与似然度的角度,可得到两随机事件之间负相依、不相依、正相依的等价条件. (四)随机事件之间相依性的等价条件 性质1.设A,B是随机试验E的任意两事件,则有以下结论. 4.任意两随机事件之间或负相依、或不相依、或正相依,三者必具其一且只具其一. 事件可看作静态的随机变量,研究动态随机变量之间的相依性更具有广泛的意义.正如条件概率是研究事件之间相依关系的工具,条件分布是研究随机变量之间相依关系的有力工具. 类似地,设连续型随机向量(X,Y)的联合分布函数H(x,y)=P(X≤x,Y≤y), 则边缘分布函数分别是:F(x)=P(X≤x)=H(x,+∞),G(y)=P(Y≤y)=H(+∞,y) (一)由分布函数刻画变量之间的相依性关系 (X,Y)独立当且仅当H(x,y)-F(x)G(y)=0; (X,Y)正象限相依当且仅当H(x,y)-F(x)G(y)≥0; (X,Y)负象限相依当且仅当H(x,y)-F(x)G(y)≤0. (二)由密度函数刻画变量之间的相依性关系 (X,Y)独立当且仅当h(x,y)-f(x)g(y)=0; (X,Y)正象限相依当且仅当h(x,y)-f(x)g(y)≥0; (X,Y)负象限相依当且仅当h(x,y)-f(x)g(y)≤0. (三)由条件分布函数刻画变量之间的相依性关系 (X,Y)独立当且仅当F(x|y)-F(x)=0; (X,Y)正象限相依当且仅当F(x|y)-F(x)≥0; (X,Y)负象限相依当且仅当F(x|y)-F(x)≤0. (四)由条件密度函数刻画变量之间的相依性关系 (X,Y)独立当且仅当f(x|y)-f(x)=0; (X,Y)正象限相依当且仅当f(x|y)-f(x)≥0; (X,Y)负象限相依当且仅当f(x|y)-f(x)≤0. (五)由条件期望刻画变量之间的相依性关系 (X,Y)独立当且仅当E(Y|X=x)=E(Y); (X,Y)正象限相依当且仅当E(Y|X=x)≥E(Y); (X,Y)负象限相依当且仅当E(Y|X=x)≤E(Y). 可知,一般地,条件期望E(Y|X=x)=α(x)是x的函数.若(X,Y)独立,则α(x)是一个常数E(Y);若(X,Y)正象限相依,则函数α(x)在直线x=E(Y)的上方;若(X,Y)负象限相依,则函数α(x)在直线x=E(Y)的下方.进一步,将条件期望E(Y|X)看成随机变量X的函数,记为E(Y|X)=α(X),称为随机变量Y对X的回归函数[11],或称为Y对X的均值回归函数,从平均的意义上刻画了变量X与Y之间的统计相依关系. 定理1.设任意二维随机向量(X,Y),q(X)是任意的可测函数,则E(Y-E(Y|X))2≤E(Y-q(X))2. 证E[Y-q(X)]2=E[(Y-E(Y|X)+(E(Y|X)-q(X))]2=E[Y-E(Y|X)]2+E[E(Y|X)-q(X)]2 +2E[(Y-E(Y|X))E(Y|X)-q(X)] 而E[(Y-E(Y|X))E(Y|X)-q(X)]=E{E[(Y-E(Y|X))(E(Y|X)-q(X))]|X}=0 故E[Y-q(X)]2=E[Y-E(Y|X)]2+E[E(Y|X)-q(X)]2≥E[Y-E(Y|X)]2 (一)贝叶斯公式中的相依性分析 分析(1)由贝叶斯公式,小孩第一次说谎后村民对小孩的信任度为 (2)因经过小孩第一次说谎后,村民对小孩的信任度由起初的先验概率P(B)=0.85修正下降为后验概率P(B|A1)=0.5313,故用P(B|A1)代替P(B),由贝叶斯公式,小孩第二次说谎后村民对小孩的信任度又降为 (二)二维正态分布中随机变量间仅存在线性相依关系 对于多维随机变量,条件分布是研究变量之间相依关系的工具,边缘分布与条件分布、边缘期望与条件期望之间的关系等都刻画了变量间的相依关系. 关于二维正态分布的边缘分布、条件分布及其变量之间的相依关系,有以下重要结论: (3)X与Y的相依性关系仅是线性关系; (4)X与Y独立当且仅当ρ=0. 证明(1)因X与Y的联合密度函数为 故关于X的边缘密度函数为 其中: (2)因为X|Y的条件密度函数为 同理,Y|X的条件密度函数为 反之,当ρ=0时,因 故X与Y独立.进一步表明对于二维正态分布,若变量间线性不相关时,则没有任何相依关系,即独立. 该定理表明,边缘分布和条件分布都依赖于联合分布;反之,仅仅由边缘分布不一定得到联合分布,因为变量间的相依结构是未知的,但是对于正态分布来讲,若变量间的相关系数已知,则联合分布是确定的,变量间也是确定的线性相依结构. 在实际问题中,变量的分布往往是未知的,需要通过回归分析方法来确定变量间的相依性关系. (三)回归分析中的相依性 例2.为了研究某一化学反应过程中温度X对产品得率Y的影响,测得数据如下: Xi100110120130140150160170180190Yi45515461667074788589 讨论随机变量X与Y的相依性关系. 分析 一般地,E(Y|X)=α(X)是随机变量Y的最佳估计,是X的函数但未必是线性函数.在回归分析中,E(Y|X)=α(X)就是变量Y对X的回归函数.实践中,往往通过观察随机变量X与Y的样本散点图来判断回归函数是线性还是非线性.在本例中,由所给X与Y的样本散点图发现这些点大致在一条直线上,因此考虑选用线性回归来讨论X与Y之间的相依性关系. 根据表中数据得, 从而, 故得出产品得率Y与温度X的回归函数为: 可知,当温度X达到165°时,产品得率Y的最佳预测值为: 在一元线性回归方程中,由于斜率项k=0.483>0,故温度X每增大一个单位,产品得率平均增大0.483个单位,说明变量X与Y之间存在正的线性相依关系。 在统计建模过程中,探究数据间的相依性关系显得尤为重要.本文主要通过由条件概率、贝叶斯公式以及似然度等方式刻画事件间的相依性关系;通过分布函数、密度函数、条件分布函数、条件密度函数以及条件期望等方式刻画随机变量间的相依性关系.讨论相依性分析的应用将事件与变量间的相依性淋漓尽致的展现出来.意义之处在于:这些指标能够较准确地刻画事件或随机变量间的相依程度,它们基本上可以克服其他度量指标的不足之处,也可以适应于各种相依类型,较准确地对复杂的相依性给出宏观或整体的度量.在概率统计的理论与应用中,往往要考察事件、随机变量间的相互依赖关系及其依赖程度,将这种相互依赖关系称为相依关系[12].直观来说,事件或变量间存在着三种不确定性相依关系:一是彼此促进关系,称为正相依关系;二是彼此抑制关系,称为负相依关系;三是彼此互不影响、互不干扰关系,称为独立关系.变量间的不确定性相依关系,按是否为线性相依,可分为线性相依关系与非线性相依关系.

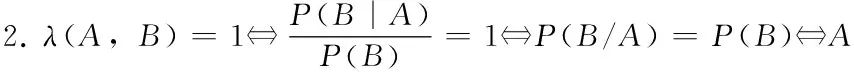
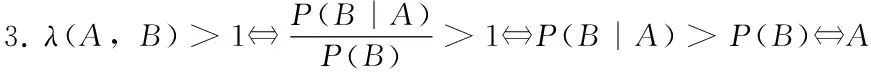
二、从不同的角度刻画变量之间的相依性



三、相依性分析的若干应用
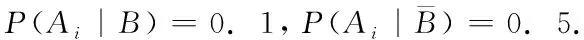

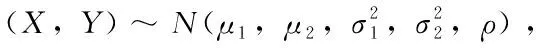

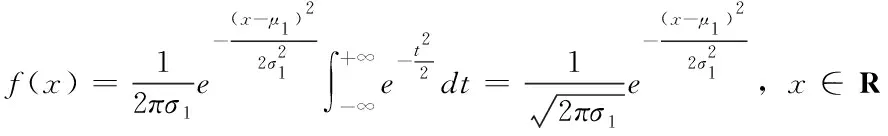








结束语
