振动筛端部预紧横梁的有限元分析*

尚凯杰，王斌华，贺朝霞

(长安大学 道路施工技术与装备教育部重点实验室，陕西 西安 710064)

0 引 言

振动筛作为一种新型高效的筛分设备广泛应用于选煤、选矿、建材、电力等行业。振动筛工况复杂，受诸多因素影响而导致筛分设备失效[1]。振动筛在工作时受到很大的交变应力，除了自身的重力、激振力以外，还会受到筛分物料的重力、下落的冲击力以及物料随着振动筛振动所产生的惯性力，所以实际工程运用中振动筛会出现各种故障从而使整个生产线停工停产。如果能够对振动筛的结构特性和动态响应有所了解，则可避免停产及经济损失，因此模态分析和谐响应分析是了解其特性的有效手段之一，既简单高效又对设备无损。柴保明等对直线振动筛进行有限元分析得到侧板危险区裂纹扩展特性、规律，以及侧板疲劳寿命和安全系数；并为了提高其寿命对加强筋的布局进行了优化[2-3]。张则荣等研究得到振动筛上横梁产生裂纹前后应变模态振型较模态频率和位移振型有显著变化；及应变模态变化率与横梁损伤程度变化关系，并且预测了上横梁疲劳损伤程度和剩余疲劳寿命[4]。李栋等对振动筛横梁进行响应分析和疲劳分析，得到动力响应情况，估算其寿命周期[5]。邵堃等研究圆振动筛筛体得出筛箱焊接后的变形量及残余应力分布[6]。张青召等研究了大型振动筛在启动过程中的运动规律[7-8]。前学者们的研究集合了振动筛大部分失效形式以及如何进行分析、结构改进，为以后的振动筛设计分析提供了宝贵的经验。目前，针对振动筛模型基本都是以实体单元为主，而笔者以板壳单元为主，再结合振动筛实际断裂位置建立局部实体模型进行计算。现以某型振动筛为例，复杂的受力导致振动筛的端部预紧横梁出现断裂，为了探究振动筛开裂原因，建立有限元模型，进行模态分析、谐响应分析，分析在给定激振工况下的受力，对其合理性进行评价。

1 振动筛简述

振动筛为双振动电机驱动，主要由筛箱、筛网、电机、阻尼弹簧、支撑管梁等组成。振动筛除了要承受自身的重力、激振力外，还会受到物料的重力、下落冲击力、物料随振动筛产生的惯性力及振动筛工作时产生的交变应力等，复杂的受力易导致振动筛产生结构破坏。振动筛筛体的主要材料Q235A，材料密度7 850 kg/m3，泊松比0.3，弹性模量E=210 GPa，材料许用应力157 MPa；振动筛的主要结构参数：激振频率16.7Hz，振动方向角58°，筛面倾角11°。

2 有限元模型的建立

2.1 单元选择

振动筛可以看作是空间板梁组合结构，因此采用ANSYS中壳单元SHELL181进行板结构的模拟；两个侧板之间以及筛网模拟采用BEAM188单元，筛网与横梁通过主从节点建立耦合达到力的传递；采用质量单元MASS21模拟物料及偏心轮质量；弹簧-阻尼单元采用COMBIN14单元进行模拟，将弹簧上节点与弹簧支座建立刚性区域达到力的传递。

2.2 物料模拟

采用MASS21单元模拟物料质量，将物料平均分配到振动筛的五层筛网上，物料与横梁建立Y向耦合以达到重力传递，筛分率为95%，物料粒径与占比如表1所列。

表1 物料粒径与占比

2.3 激振力模拟

使用MASS21单元模拟偏心块质量，将两个质点与电机横梁对应螺栓位置进行耦合建立刚性区域以达到激振力的传递。电机激振力为2×245 kN，静扭矩2×2 236 kg·mm。由已知振动方向角58°，筛面倾角11°，激振力有效传递90%，为在ANSYS中方便施加激振力，将激振力分解为X向与Y向分力，两分力分别为：

X方向分力：

Fx=Fcos 58°×90%

=245 000×cos 58°×90%≈116 847 N

(1)

Y方向分力：

Fy=Fsin 58°×90%

=245 000×sin 58°×90%≈186 995 N

(2)

2.4 支撑弹簧模拟

根据振动筛实际工况，在弹簧支座处建立弹簧单元，纵向弹簧模拟实际弹簧竖向刚度。由于振动筛在电机产生的激振力作用下会产生轴向与横向的振动，因此利用COMBIN14单元模拟弹簧时，增加横向弹簧来模拟实际弹簧的横向刚度。

综上：可得振动筛有限元模型如图1、2所示。

图1 振动筛有限元模型(含边界条件) 图2 振动筛有限元模型(不含边界条件)

3 有限元模型模态分析

模态分析是动力学分析基础，模态分析可以确定结构的固有频率和振型。设置最大提取模态阶数为10，采用分块Lanczos法提取振动筛的模态频率和振型等模态参数[9]。对于一般结构，要求各阶固有频率要远离工作频率，具体是要求工作频率不落在某阶固有频率的半功率带宽内；对结构振动贡献较大的振型不影响其正常工作[10]。模态频率结果如表2所列。第7、8阶模态振型分别如图3、4所示。

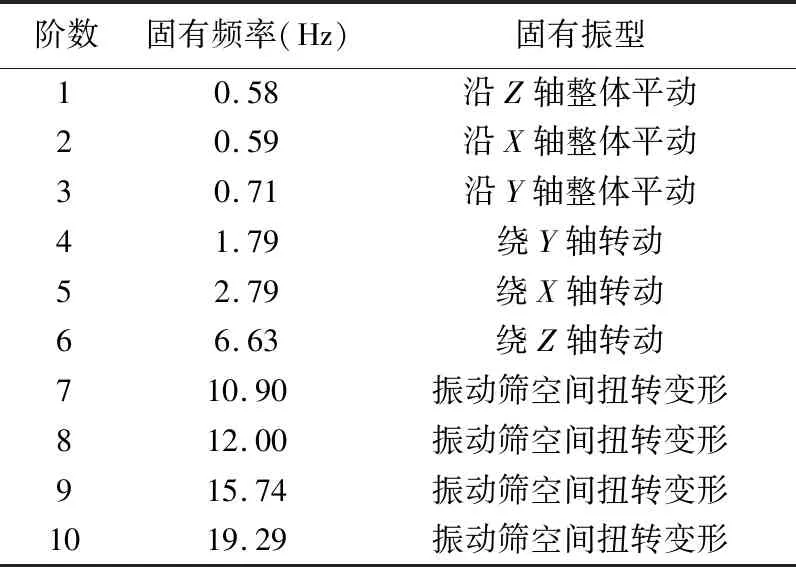
表2 模态频率结果

图3 振动筛第7阶模态振型图 图4 振动筛第8阶模态振型图

由表2可知，前6阶模态为刚体的平动与转动，其余模态振型为弹性变形。第7阶模态频率为10.93 Hz，第12阶模态频率为19.37 Hz，对应振型为空间扭动，而振动筛的工作频率为16.7 Hz，远离其固有频率，说明振动筛模态频率分布合理。

4 振动筛出口端梁谐响应分析

振动筛在工作时由电机带动激振器产生交变激振力，振动筛横梁、筛框、激振器横梁都会产生动应力，为了进一步了解动应力数值及分布规律，需对振动筛进行谐响应分析。考虑实际断裂位置，选择出口端的预紧力横梁为主要分析对象。

4.1 预紧端梁启动阶段应力分析

设置分析频率为0～100 Hz，采用完全法对振动筛进行谐响应分析。由实际振动筛预紧力梁断裂位置选出五根横梁中的第二根横梁，由于有限元模型节点众多，选出断裂位置具有代表性的节点编号797 542，查看其应力-频率图如图5所示。由第一主应力的应力幅-频谱图可知：振动筛在频率0.7 Hz与6.6 Hz时均出现高应力峰值，说明在实际工作过程中，振动筛电机启停时会出现瞬时高应力状态，读取预紧力横梁二在Freq=0.7 Hz和Freq=6.6 Hz时的S1应力云图如图6、7所示。由此可知振动筛在电机启停过程出现的瞬时大应力会导致结构易出现断裂，这也与实际断裂位置相符，说明该分析方法合理，可用于指导产品改进。

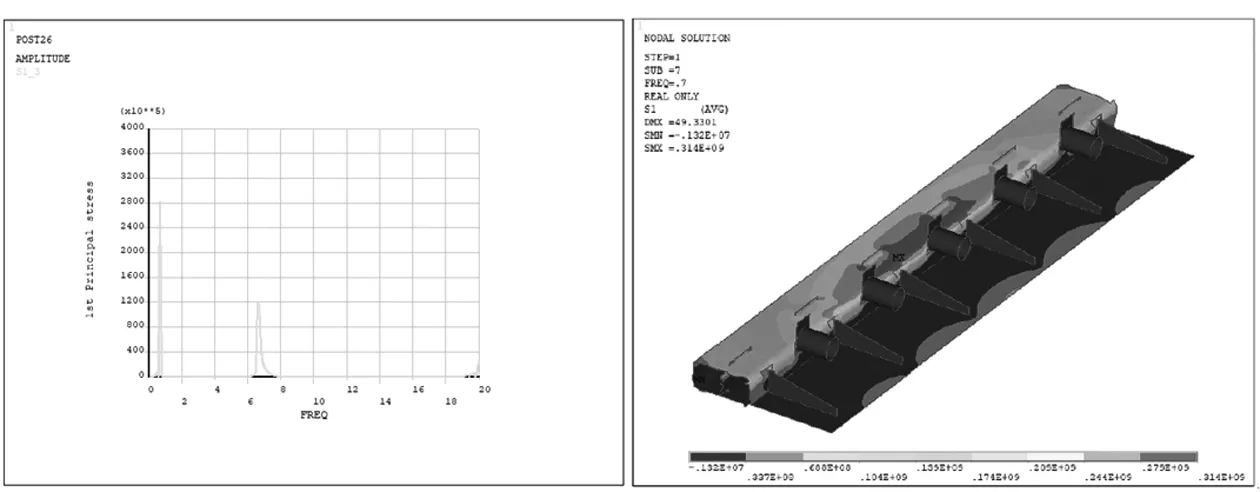
图5 横梁二跨中位置焊接处S1应力幅-频谱图 图6 横梁二Freq=0.7 HzS1应力云图

图7 横梁二Freq=6.6 HzS1应力云图 图8 Freq=16.7预紧梁S1应力云图

4.2 预紧端梁工作频率段应力分析

图8为振动筛预紧力横梁在工作频率16.7 Hz下的等效应力分布云图。由图12可以看出预紧力梁最大应力位置出现在梁的两端，最大应力值为32.7 MPa，其余位置应力均比较小，都低于材料许用应力，说明振动筛在工作状态下满足要求。

5 振动筛焊缝区精细有限元分析

为了精确分析危险构造细节的应力状态，将关键构造细节转换成实体模型结构进行精细分析。采用实体单元SOLID186单元模拟，并根据实际焊接加工图建立焊缝构造，实体单元与板壳单元的连接采用接触单元，设置MPC(即多点约束方程)算法，通过MPC可将SHELL单元与SOLID单元进行连接计算,MPC不需要连接处节点一一对应便可将不连续、自由度不协调的单元连接，本质为设置接触单元的接触算法为MPC algorithm，并定义接触面行为绑定来实现。实体单元模型如图9所示，实体单元与板壳元连接如图10、11所示。

图9 实体单元模型图 图10 实体单元与板壳元连接

通过谐响应分析计算，得出实体模型段焊缝区域第一主应力的应力幅-频谱图，选择代表节点938 624和938 636，如图12所示。由图可知振动筛在Freq=0.7 Hz与Freq=6.7 Hz时出现高应力峰值，获得其对应频率的应力云图如图13、14所示。

图11 局部实体单元与板壳元连接图 图12 焊缝区域S1应力幅-频谱图

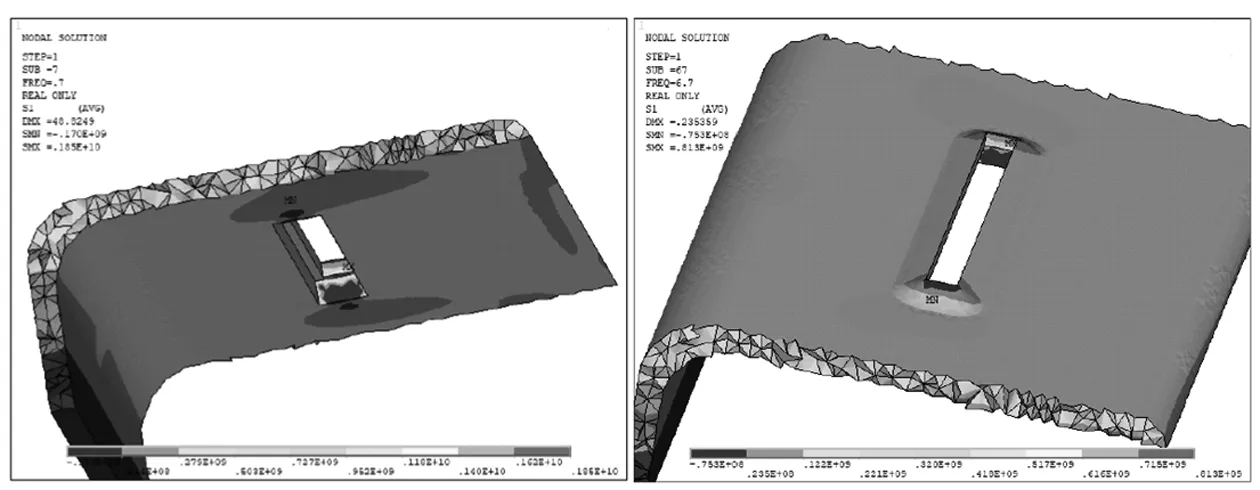
图13 上表面焊缝区域应力云图Freq=0.7 Hz 图14 上表面焊缝区域应力云图Freq=6.7 Hz

由此可知振动筛在低频时横梁跨中段出现应力集中，频率为0.7 Hz时最大应力集中1 850 MPa，频率为6.7 Hz时最大应力集中813 MPa，假定材料的弹性变形没有考虑材料的塑性屈服，因此应力值只反映应力集中程度，并不代表真实应力值，该应力值明显大于材料屈服强度，因此应力集中明显，设备启停过程中易发生瞬时应力峰值导致裂纹萌生，说明实际结构此处容易出现断裂[11-12]。

6 结 论

以某公司设计的振动筛为例，结合振动筛实际工况建立了有限元模型，并进行了模态分析及谐响应分析，最终得出以下结论：

(1) 振动筛整体结构模态分析结果表明，振动筛固有频率避开了工作频率16.7 Hz，正常运行阶段不会出现共振现象。

(2) 振动筛的谐响应曲线以及应力结果表明，振动筛预紧力横梁大应力的发生频率出现在0.7 Hz及6.7 Hz附近，表明振动筛含料每次启动或者停止过程中会出现极大的瞬时应力，导致结构裂纹萌生和扩展。

通过对振动筛进行三维建模、有限元分析得出振动筛设备端部预紧横梁开裂原因，对振动筛结构改进具有参考意义。但振动筛工作时可能会有些非线性状况，而谐响应适用于规律变量，具有局限性，所以在非线性方面要做更加深入的研究来弥补谐响应分析的不足，进而更好的将理论应用于实际。