基于MRI-CGCM3模式和遗传编程人工智能算法的逐日参考作物腾发量预报方法

姚顺秋，闫晓惠

(1.大连市庄河水利建筑勘测设计院，辽宁 大连 116400；2.加拿大渥太华大学，安大略 渥太华 K1N6N5)

作物腾发量是指作物叶面蒸腾量与颗间蒸发量之和，它的估算是作物需水量计算的基础，也因此是精准灌溉与排水设计的重要环节[1- 2]。作物腾发量可以表示为作物系数与参考作物腾发量(ET0)的乘积，而各类作物的作物系数基本为恒定值，因此，预报ET0是预报作物腾发量的关键、具有重要的现实意义[3- 5]。ET0的预报大体可以分为直接法和间接法两种。直接法主要是根据历史数据序列并采用基于数理统计原理的方法来对未来的ET0进行预测。间接法主要是通过气象预报数据并采用基于物理原理的ET0公式来对其进行预测。应用直接法可以对未来的演变趋势进行较为便捷迅速的判断，但是，在全球气候显著变化的条件下，历史数据的统计规律已难以完全切合未来的演变趋势，因此直接法在逐日ET0的预测中已较难取得理想的精确度。

随着近几年气象预测与模拟技术的发展，采用间接法预报逐日ET0正逐渐流行。例如闫晓惠等人[6]提出了基于全球气候变化模式和Penman-Monteith公式的长期逐日ET0预报方法，并应用该方法对加拿大渥太华、温哥华、温尼伯等城市的ET0进行计算，结果证明基于该方法的预测值满足精度要求。该方法的一个限制条件是它一般必须要求降尺度操作，操作复杂，且需要详细的气温、日照、风速和湿度历史数据，在资料缺乏的地区较难推广使用。近年来，人工智能与机器学习技术得到了飞速的发展，例如，闫晓惠等人[7- 11]采用将遗传编程和多基因遗传编程等方法应用在了不同的水利问题中，取得非常好的效果。该方法主要具有3项重要优势：①可以降低人为操作的复杂性；②可以规避人为假设的不合理性；③可以深度挖掘数据本身之间的隐藏关系，从而可以更为准确地表达数据之间的联系。因此，本文提出基于MRI-CGCM3模式和遗传编程人工智能算法的逐日ET0预报方法(以下简称为“GCM-GP法”)，首先基于实测气温数据、采用Hargreaves公式计算了大连市庄河地区2011年7月1日至2020年3月31日间的ET0。分别采用MRI-CGCM3模式的原始模拟数据(以下简称为“GCM法”)和GCM-GP法计算了该地区的ET0，并与实际数据进行比较，为提升ET0预报的效率与精确度提供参考。

1 方法

1.1 ET0计算方法

大连庄河位于辽宁省东南部，黄海北岸，是辽南地区重要的水源地，近几年水资源压力不断上升，优化灌溉排水方案对于该地区的水资源利用与保护成为极为重要的措施，而ET0的准确预报又是灌溉排水规划的最重要环节之一，因此该地区亟需提高ET0的预测精度。获取该庄河地区2011年7月1日至2020年3月31日的逐日最高与最低气温数据，数据共3197组。该地区采用Hargreaves 公式[12]计算ET0，该公式可以表示为:

(1)

式中，T—日最高气温与最低气温的平均值，℃；Rs—太阳辐射，MJ/(m2·d)。

Rs可通过下式计算[13]：

(2)

式中，KRs—经验系数，对于内陆地区其值一般设定为0.16，而对于沿海地区其值一般设定为019，Tmax、Tmin—日最高和最低气温；Ra—地外辐射，MJ/(m2·d)。

Ra的计算公式为[14]:

(3)

式中，GSC—太阳常数，为 0.0820;dr—日地相对距离;ωs—日落时角;φ—维度;δ—太阳偏磁角。

日地相对距离dr和太阳偏磁角δ的计算公式为：

(4)

(5)

式中，J—日序号。

日落时角ωs的计算公式为：

ωs=arccos[-tanφtanδ]

(6)

1.2 MRI-CGCM3模式

MRI-CGCM3是由气象研究中心(Meteorological Research Institute: MRI)在2012年开发的一款全球气候模式。它主要是在第5代耦合模式比较计划(CMIP5)框架下开发，在MRI-CGCM2系列版本上进行更新与改进而成。该模式主要可提供气温(包括最高、最低和平均气温)、降雨、海平面气压、风速和降雪5项气象模拟数据。目前，在各项气象因子的预测中，气温的预测精确度一般较高，而Hargreaves公式中只需要逐日气温数据，因此，选取其中的逐日最高和最低气温。采用MATLAB程序提取庄河地区所在位置(39.6808°N，122.9673°E)的数据。

1.3 遗传编程

遗传编程也称基因编程，它是一种利用进化算法的机器学习技术，它主要是受达尔文进化论的启发，是借鉴生物演化过程而产生的一种可以构造算法的算法。它首先随机生成模型库，之后对模型进行性能评价，再通过基因繁殖(Reproduction)、基因突变(Mutation)和基因交叉(Crossover)等运算来对模型进行演化，最终得到满意的模型。本文采用该算法来建立ET0模型并进行ET0的计算，不同于传统的模型，在该方法中，输入量为MRI-CGCM3模式的气温数据，输出量为实际的ET0，因此采用该算法得到的最终模型可以直接表示MRI-CGCM3模式气温数据与实际ET0之间的关系，省却了降尺度与地区修正等操作过程，因此，模型建立后的使用非常简便。

1.4 性能评价

为深入量化预报方法的精确度，计算模拟值与实测值之间的均方根误差(RMSE)和决定系数值(R2)，其公式如下。

均方根差：

(7)

决定系数：

(8)

式中，xs—实测值；xm—模拟值。

2 结果与讨论

2.1 逐日气温实测与模拟值

提取并整理研究时间范围内逐日最高与最低气温的实测与MRI-CGCM3模拟值(以下简称“模拟值”)，结果呈现于图2中，其中圆点表示实测值，实线代表模拟值。由图可知，模拟逐日气温随时间的变化趋势与实测值基本保持一致，各散点的分布较接近于实测值。实测逐日最高气温数据序列中的最低值与最高值分别为-19°和35℃，而模拟值数据序列中的最低值与最高值分别为-20℃和33℃，两组数据相差较小。实测逐日最低气温数据序列中的最低值与最高值分别为-23°和26℃，而模拟值数据序列中的最低值与最高值同样也分别为-23℃和26℃，与实测数据完全一致。因此，MRI-CGCM3模拟值较为合理，可以用于后续的计算与分析中。

图1 逐日最高与最低气温实测值与模拟值

2.2 基于GCM法的ET0预报结果

图2比较了基于实测数据的ET0计算结果(以下简称“实际值”)和基于GCM法的计算结果(以下简称“GCM模拟值”)。大多数的各数据点均分布在等值线附近，说明GCM模拟值与实际值的吻合度较好，但部分散点超过了20%的范围。多数超过20%范围的散点位于等值线的下侧，即采用当前的方法可能低估实际的ET0值。因此，该方法的精确度有待提高。GCM模拟结果的RMSE值为1.099毫米/天、R2值为0.76。

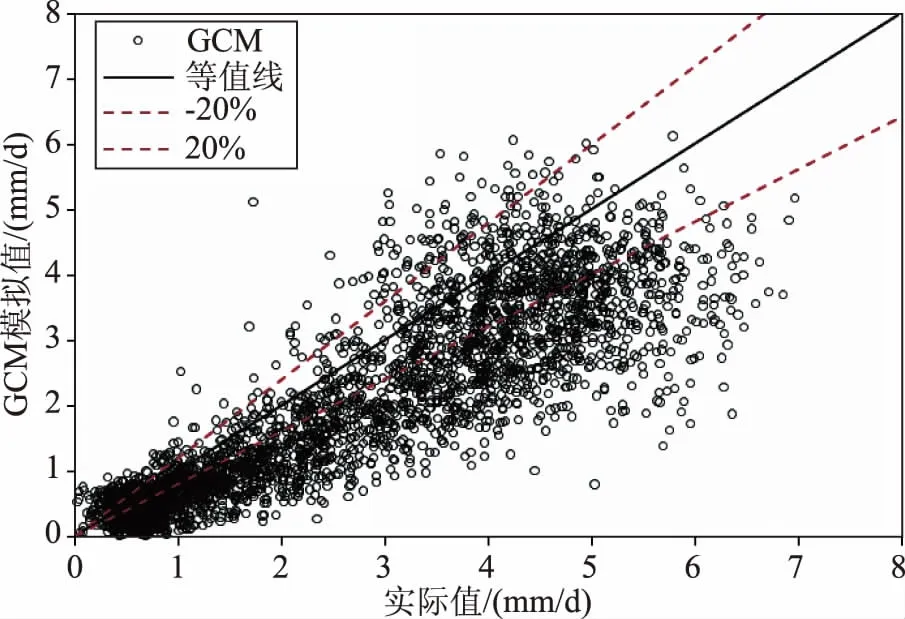
图2 逐日ET0的实测值与GCM模拟值

2.3 基于GCM-GP的ET0预报结果

采用MATLAB程序从3197组数据中随机选取80%用于模型训练，剩余20%的数据用于模型验证。从MRI-CGCM3模式中得到逐日最高与最低气温数据并定义为输入量，选用实际的ET0值为输出量，采用该算法将得到一个新的ET0模型，之后可以采用该模型和输入量计算输出量。该算法首先随机生成一个能够拟合特定数据集的函数库(此处设定为500个函数)，因此在初代时其误差较大(平均RMSE值约为1.25)。随着进化代数的增加，该算法通过基因繁殖、基因突变和基因交叉等运算来对函数模型进行演化与改进，因此模型的误差值不断减小(图3)。根据图3可知，当代数达到约50时，其误差随代数的变化已经较小，即运行更多的进化代数将不再显著提升模型性能。因此，将最大进化代数设置为300，而最终得到的最佳函数模型可以简化表示为：

y=0.00149 log(x1-1.0 absx2)2+0.00149 abs(10.0x1-5.0x2+sin(x1+2.0x2)+log(sin2.0x1)+28.5)+0.00149 abs(3.0x1-1.0x2+sin(x1+2.0x2)-14.2)-0.00298 sinx1+0.00149(x1+x2+21.2)(2.0x1-2.0x2+abs(3.0x1-2.0x2)+7.11)-0.00149x1(3.0x1-2.0x2-1.0 log(x1-2.0x2+7.03)2+abs(3.0x2-2.0x1+0.463)+7.11)-0.00149 abs(cos(x2-1.0x1+7.15)+log(x2/(x2+7.11))(8.0x1-7.0x2+sinx1-35.5)-0.108

式中，y—输出量(ET0)；x1—输入变量1(日最高气温)；x2—输入变量2(日最低气温)。

图3 模型训练演化过程

采用该模型计算ET0值(以下称为GCM-GP模拟值)，并与实际值进行对比，如图4所示。

其中用于模型训练的数据序列的RMSE和R2值分别为0.37mm/d和0.93，而用于模型验证的数据序列的RMSE和R2值分别为0.37mm/d和0.94。两者相差不大，说明模型性能稳定。相对于GCM结果，其RMSE值降低了约66%，而R2值提高了约24%，因此可以认为该方法可以使得ET0的精确度大幅度提升、具有非常好的推广价值。

图4 ET0的实际值(菱形)与GCM-GP模拟值(实线)

3 结语

采用庄河地区2011年7月1日至2020年3月31日逐日气温观测数据与Hargreaves模型计算了该地区的逐日ET0。提出了基于MRI-CGCM3模式与遗传编程人工智能算法(GCM-GP)的ET0估算方法，并分别用两种方法对ET0进行预报。

结果表明，两种方法所得结果的变化趋势基本与实测结果保持一致，但GCM-GP方法可以显著提高ET0的模拟精确度(相对于GCM法，其RMSE值降低了约66%，而R2值提高了约24%)，具有非常好的推广价值。本文在实际ET0的计算中采用的是Hargreaves模型，但是在资料比较充足的地区，Penman-Monteith公式的使用则更为普遍，因此，在下一步的研究中，可以采用相同的方法训练出对应于Penman-Monteith公式的ET0预报模型，也可以采用该方法建立其它地区的ET0模型。