基于GPU并行优化的网格参数化算法

吴 璇，张举勇

(中国科学技术大学 数学科学学院，安徽 合肥 230026）

0 引言

三维模型是一种使用三维曲面来表述物体的三维数据，网格是三维模型中一种应用广泛的表达方式。随着数字几何处理技术的发展以及扫描技术的进步，网格模型得以广泛应用于动画、游戏、建筑、医疗、工业设计等行业。网格曲面参数化是流形曲面和参数域之间的一一映射，是网格处理领域中不可或缺的基础工具，在网格变形、纹理映射、网格压缩中都发挥着重要作用。通常网格是在3D空间中的二维曲面，直接对于3D模型进行网格处理非常复杂，通过一一映射到简单的参数域，得到的参数化结果与原始网格有相同的拓扑结构以及尽可能小的失真，然后在参数域上进行网格处理，极大地降低了处理难度。

一个高质量的参数化映射f有以下性质：无翻转、低失真度量。无翻转意味着 det J(f）>0，这里 J(f）是f的雅各比矩阵。理想中的映射是在映射后网格与初始网格之间没有形变，但这只是理想情况，一个高质量的网格需要尽量减少形变，而失真度量就是用于衡量映射形变的数值。

经典的参数化方法主要分为线性方法与非线性方法两种。线性方法计算简单，可扩展性强，因为线性方法通过计算一个线性系统来得到参数化结果。虽然线性方法在计算效率上占据优势，但是有许多方法都必须固定边界，无法获得自由边界的参数化结果，比如针对拓扑圆盘，FLOATER M[1-2]通过把边界固定到一个凸多边形上，同时所有权重都保证为正数，得到一个无翻转的参数化结果。自由边界的方法可以通过虚拟边界、增添线性方程来实现。自由边界方法通常可以减少固定边界造成大的变形扭曲，却不一定确保得到的映射是无翻转的。非线性方法通常构造出一个以变形能量为目标式，包含无翻转硬约束的全局优化问题[3-4]，使用牛顿法、高斯牛顿法等优化算法降低参数化网格的变形能量，这些能量函数描述了参数化映射后网格的变形、失真程度，通常是高度非线性、非凸的，所以这些方法计算效率低，而且在处理大型网格时，非线性方法通常会随着所处理网格的增大，收敛速度极大地降低。

为了解决以往参数化方法运算消耗大、运算效率低、非并行、可扩展性差的缺陷，本文提出了一种可并行、可扩展计算无翻转、高质量参数化网格的算法。不同于以往算法构造出一个无法并行的全局优化问题，本文算法通过引入辅助变量，把参数化问题分解为每个面上，每条内边上的局部子问题。该算法的空间复杂度与网格模型规模成线性关系，也就是 4N+2|εint|， 其中 N 是网格的 面数 ，|εint|是网格内边条数。相比于现存算法不可并行性，本文算法最大创新点在于每次迭代都可以并行处理N个关于三角面片上映射的子问题以及|εint|个关于内边相容性约束的子问题。实验显示相比于现存算法，本文算法最终得到相同甚至更好质量网格所需运算时间缩短了至少百倍以上。随着扫描技术的飞快发展，3D网格模型的规模越来越大，可扩展的网格参数化算法意义重大。但计算大规模网格的无翻转映射是一个具有挑战性的难题，该算法可扩展，长于处理大型网格模型。

1 相关工作

1.1 无翻转映射

良好的参数化结果需要具有无翻转的性质。TUTTE嵌入及其变体在理论上保证参数化映射无翻转，但基本上都会引入大的失真变形。基于表示的方法[4-5]无法确保消除所有翻转，固定边界方法总是可以产生无翻转参数化映射，但在边界不适宜的情况下往往带来大的失真变形。基于维护的方法[6-7]开始优化失真能量的同时保持无翻转。然而，这些数值算法往往需要解决一个全局优化问题，以至于不可并行以及可扩展性差。比如HORMANN K等人提出了MIPS方法[7]，可以获得自由边界的参数化结果，但是MIPS能量计算耗时久且容易陷入局部最小点。有界失真方法，比如LIPMAN Y等提出的方法[8-9]直接限制了失真度量的大小，但计算效率低，而且如何设置一个保证无翻转的合适边界成为难题。不同于以上方法，采用了一种局部推进策略来解决复杂的网格参数化问题，算法是可并行和可扩展的。为了产生无翻转映射，一个直接的方法是从一个无翻转的初始值开始优化，然后使用一个防翻转能量，通常防翻转能量在翻转出现时将会变为无穷大。这样优化问题的结果会保证属于可行域。比如之前的一些研究工作[10-13]，采用的方法中也使用一个无翻转的映射作为初始值[12]，如果存在翻转，则会将其映射到无翻转的可行域中。在使用ADMM算法优化的过程中，用矩阵Ai来表示三角曲面i的映射矩阵，在ADMM算法的A子问题中，使用牛顿法来迭代A，在迭代中使用线搜索来保证每个三角曲面上的映射矩阵的行列式大于0。这样保证了算法结果始终处于无翻转的可行域中。

1.2 ADMM算法

ADMM是一种强大的优化算法，因为其适合处理大型问题以及可以高度并行化，通过与GPU结合，在信号处理、计算机视觉、图像处理、自动控制等领域有着广泛的应用[14-18]。ADMM算法一开始用来处理凸问题，实际上，它在处理非凸问题上也有很好的表现[19-21]。该算法把一个全局的优化问题分解为小的局部问题。通常处理以下形式的问题：

就像SA算法，在分散网格后，必须保证网格可以拼接起来，以及如果想要处理网格变形，还得保证满足控制点约束。在本文中，通过引入辅助变量[22]，全局的优化问题被分解成了每个三角曲面上包含两个子问题的优化问题。这两个子问题分别对应着网格拼接，能量优化两个方面。

2 可并行参数化算法

2.1 问题描述

考虑 3D网格 M 上的参数化映射 M={A1，A2，…，AN}。映射的原始网格是3D三角网格M，该三角网格包含 Nv个顶 点{vi，i=1，… ，Nv}，Ne条 边{ei，i=1，…，Ne}，N 个三 角面片{si，i=1，… ，N}，εint是包含三角网格M所有内边的集合。在每一个面片si上构建局部坐标系，面片上的点在局部坐标系中表示为 v=(x1，x2）∈R2，参数域上的点表示为 u=(u1，u2）∈R2。 用{Ai，Ti}来表示面片 si上的仿射变换 Ai，其中Ai∈R2×2是线性变换矩阵，Ti∈R2是平移向量。 面片si上的点 v映射后的结果u为 Aiv+Ti。三角网格M上的映射是无翻转的当且只当 det(Ai）>0，i=1，…，N。使用MIPS能量来度量映射误差。对于每个三角形曲面，映射被定义成了一个仿射变换：

对于每个三角曲面，MIPS能量有以下表示：

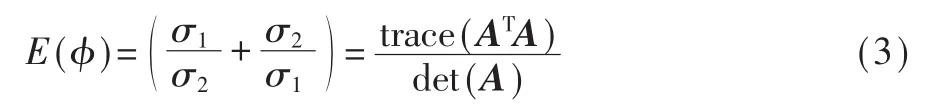
其中 σ1、σ2是线性变换矩阵 A有符号的奇异值。优化问题被构造成以下形式：

2.2 ADMM算法

对于该优化问题使用ADMM算法来解决。首先，把所有三角曲面上的变换矩阵Ai连接成一个矩阵 A∈R2×2N。 然 后 引 入 辅 助 变 量 ：Y∈R2×4|εint|，它 对应于相邻三角曲面上的线性映射的相容性约束常见符号如表 1 所示。

表1 常见符号表

可以把该问题重写为以下形式：

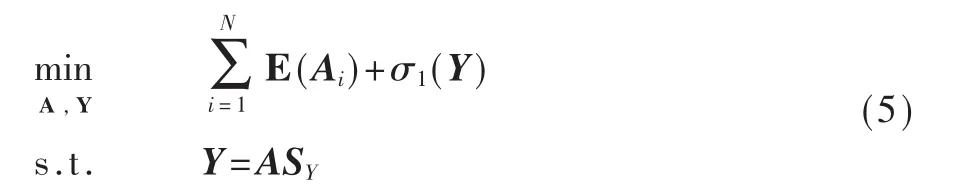
这里 σ1是相容性约束的示性函数。 SY∈R2N×4|εint|是稀疏的选择矩阵，则有：

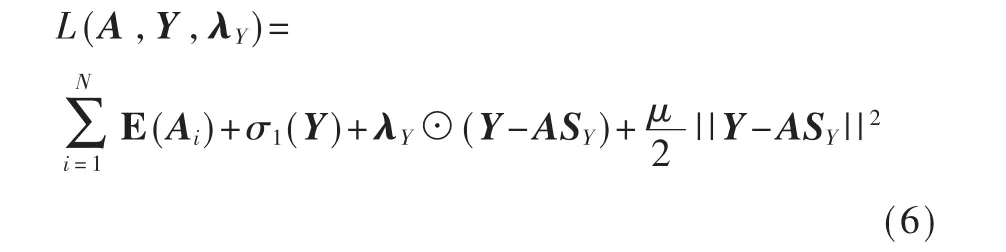
其中λY是对偶变量，⊙是系数乘法，μ是惩罚系数。算法的主流程见图2。

本算法的初始参数化映射M0通过使用简单的参数化算法 Linear ABF[12]获得，相对应的初始参数化网格为 M0：=M0(M）。

把每个面片上的仿射变换作为优化变量，构造优化问题，引入辅助变量，应用ADMM算法处理优化问题，获取最终的参数化映射Mfinal。

等到算法收敛后，从Mfinal中恢复出相对应的参数化网格 Mfinal。

2.2.1 固定 A，更新 Y

图1 相容性约束示意图

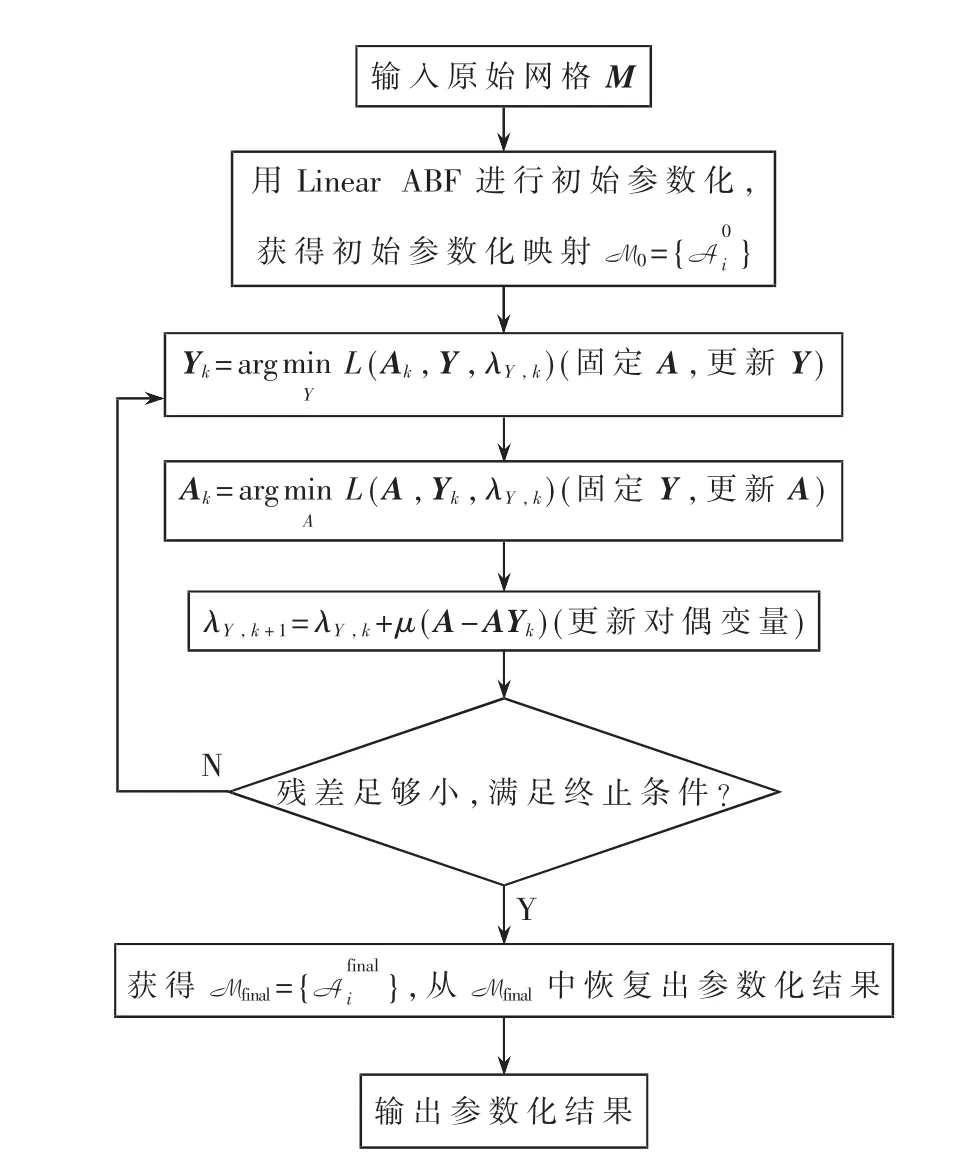
图2 算法流程图

2.2.2 固定 Y，更新 A

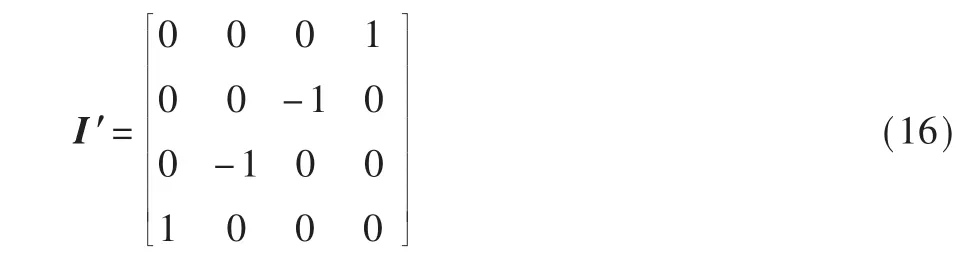
其 中 β=μ(|y(i）|），V1=(a，b，c，d）T是 将 Ai的 元 素 列成一列，V2=(d，-c，-b，a）T，sign 是符号函数，I是一个 4×4的单位矩阵，I′有以下表示形式：

使用牛顿法来解决这个问题，更新流程如下，对于三角曲面i上的变换矩阵有：

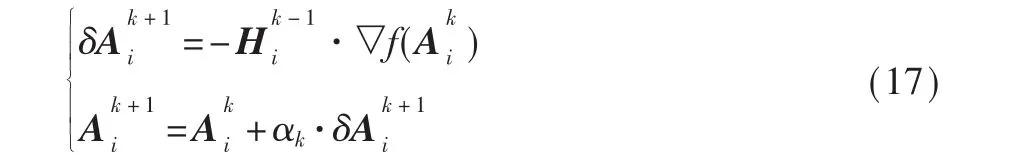
令 α0=1，αk用 αk-1初始化，如果 αk使目标式fs(Ai）上升，则乘以0.5来更新步长，直到目标式下降。为了确保无翻转，在线搜索的过程中必须保证det(Ai）>0，在 线 搜 索 中 目 标 式 fs(Ai）在det(Ai）＜0时 设 置 无 穷大 ，det(Ai）>0 时 fs(Ai）=f(Ai）。

2.2.3 更新对偶变量

用该公式更新 λY：

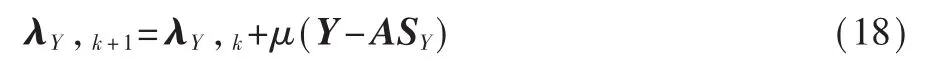
2.2.4 初始化与终止条件

上述算法需要给出每个三角曲面上的初始变换矩阵。使用一些参数化方法来计算原始网格的参数化结果来得到初始的参数化结果，本次实验中主要采用的方法是Linear ABF参数化方法，除此以外还可以使用TUTTE嵌入。认定当||rprimal||2小于0.000 3且||rprimal||2小于1e-5的时候，ADMM算法收敛。

2.2.5 网格恢复

在优化算法收敛后，将得到每个三角曲面上的变换矩阵Ai，而网格顶点在参数域上的坐标可以从变换矩阵中恢复出来。为进行这一系列过程，从顶点v0出发，进行广度优先遍历构造以下点集：

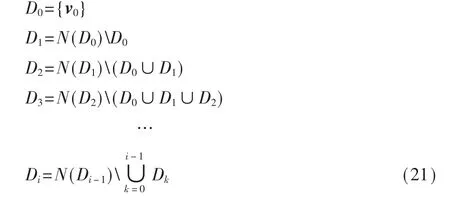
其中 N(·）是一环相邻顶点的集合，D0表示包含顶点v0的集合，Di表示距离D0中任意一个顶点最短路径正好包含i-1条边的顶点的集合。所有的集合都根据从D0中顶点出发的广度优先搜索来决定。构造过程为从D0中取出点v0作为根节点，找到它未遍历过的相邻点，放入 D1中，成为v0的子节点，然后依次取出D1中的顶点，遍历未访问的顶点，构造D2，这样依次构造点集，直到网格中所有的顶点都被遍历过。

依次计算D0，D1…中顶点的在参数域中的位置，当已经计算出来Di中顶点va在参数域中的位置时 u(va），依照以下公式恢复出 Di+1中 va的子节点——顶点vb在参数域中的位置u(vb）：

其中A*是连接两个顶点 va、vb的边任一相邻三角面片上的变换矩阵。当Di中所有顶点都被计算出参数域中位置之后，再依次计算Di+1中顶点在参数域中的位置。

3 实验结果

网格参数化上的实验环境是一台2.50 GHz的Intel Core i5的笔记本电脑，RAM为 8 GB，GPU是GeForce 940MX。利用CUDA加速时，使用的是cuda 9.0。核函数中每个块中有64个线程数，块的个数则由该子问题总共有多少并行计算的元素来决定的，例如在 A子问题中，三角曲面的个数N将分散到⎿N/64」个块上。牛顿法中，线搜索中α=0.5，同时当梯度的范数▽f小于1e-3时，终止牛顿法。为了更加公正地对比不同方法得到的映射的质量，使用文献[24]中的方法来统一质量度量。对于每一个三角曲面sj，采用保角损失度量其中 σj，1、σj，2是三角曲面 j上的 映射 Aj的奇异 值。用来表示所有三角曲面上的保角损失度量的平均值。

3.1 网格参数化

图3展示了三角网格参数化结果。图中原始网格之后紧跟的是该网格的参数化结果，第一个是SA算法的结果，第二个是本文算法的结果，使用的初始值都是由Linear ABF算法得到的。在参数化结果下面标注着算法计算时间以及得到的参数化结果的平均保角度损失度量。可以看出，本文的算法在bunny与bimba这两个例子上展现了极大的优势，这是因为这两个网格相比于male，disk是大型网格（bunny有 1 251 046个顶点，bimba有 30 268个顶点），可以看到本文的算法因为高度并行化的缘故，长于处理大型网格，在计算速度上占有极大的优势。同时，将本文算法同 SLIM[23]、AMIPS[24]算法进行比较，结果展示在表2中，可以看出本文算法得到高质量网格的同时，运算时间基本缩短了至少百倍以上，比如tooth，SLIM算法所用时间是本文算法的23 726倍。图4展示了网格大小递进的gargoyle模型MIPS能量下降趋势，证明本文算法的可扩展性，大多数算法在模型点数超过150k时，收敛会变慢，本文算法却在网格模型变大为320k个面时，保持着近乎一致的收敛速度。

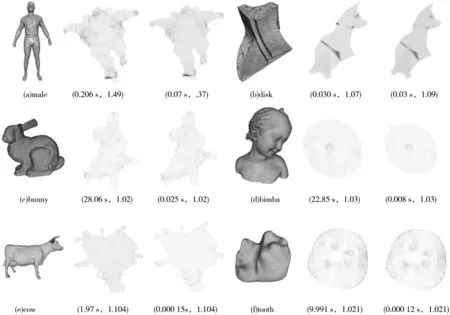
图3 网格参数化结果展示

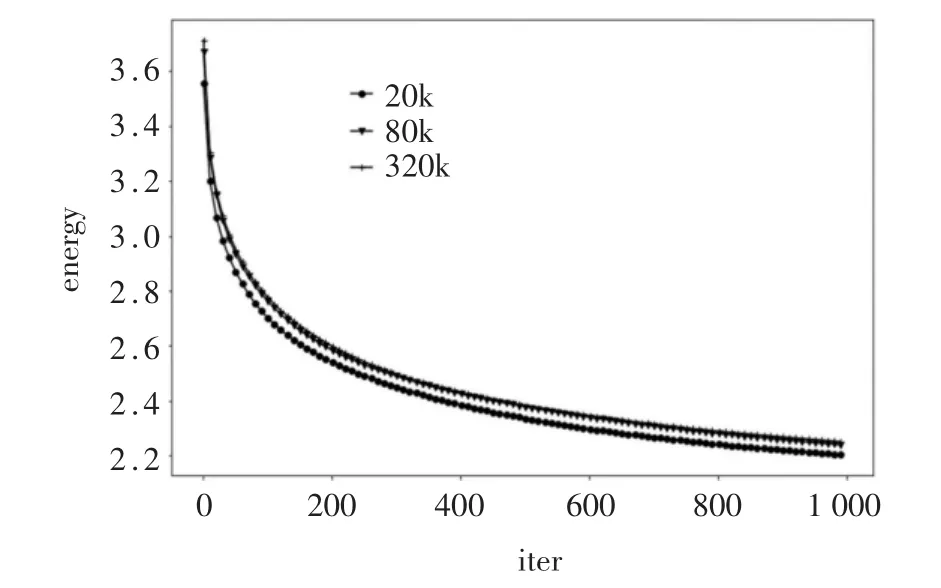
图4 不同大小网格迭代趋势图

3.2 不同惩罚系数

图5为不同惩罚系数下网格参数化的结果。对于camel，在惩罚系数为90 000时的最终收敛结果的平均保角度损失度量为1.32，收敛时间为0.025 s，在惩罚系数为30 000时的最终收敛结果平均保角度损失度量为 1.25，收敛时间为 0.064 s；对于 isis，在惩罚系数为50 000时的最终平均保角度损失度量为1.118，收敛时间为 0.003 5 s，在惩罚系数为 10 000时的最终平均保角度损失度量为1.099，收敛时间为0.058 s。注意当惩罚系数过低的时候，将出现不收敛的情况。但参考表3，惩罚系数整体来说有相当大的范围都会收敛，比如对tooth进行保角映射，在惩罚系数1 000到50 000都是收敛的。对于MIPS能量，通常可以选择10 000。对于对称狄利克雷能量，惩罚系数通常可以选择500。

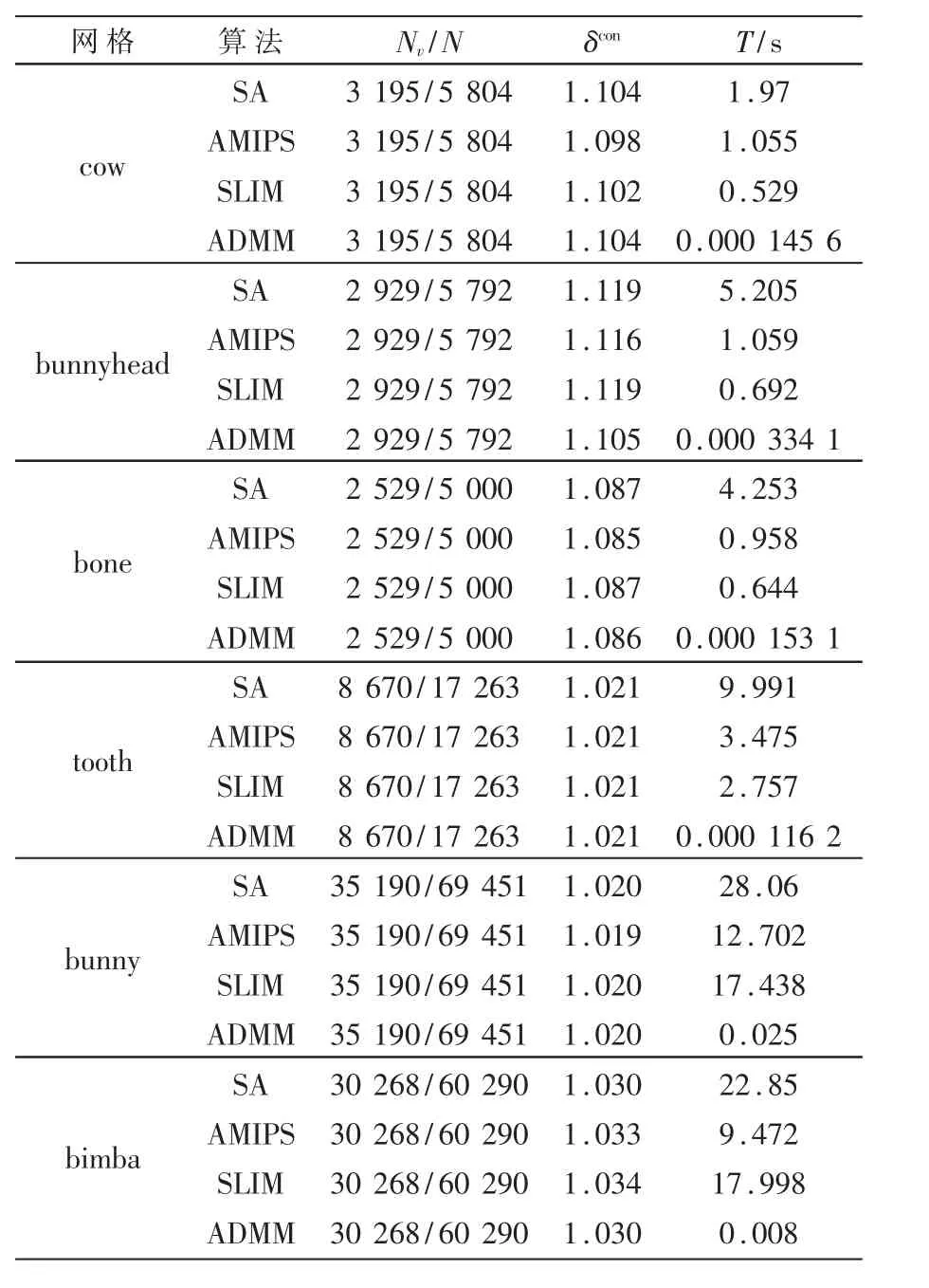
表2 参数化算法运行时间比较

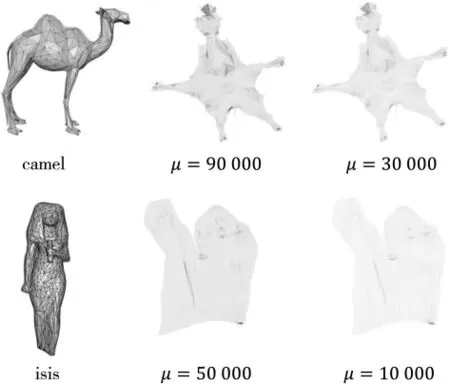
图5 不同惩罚系数参数化结果图

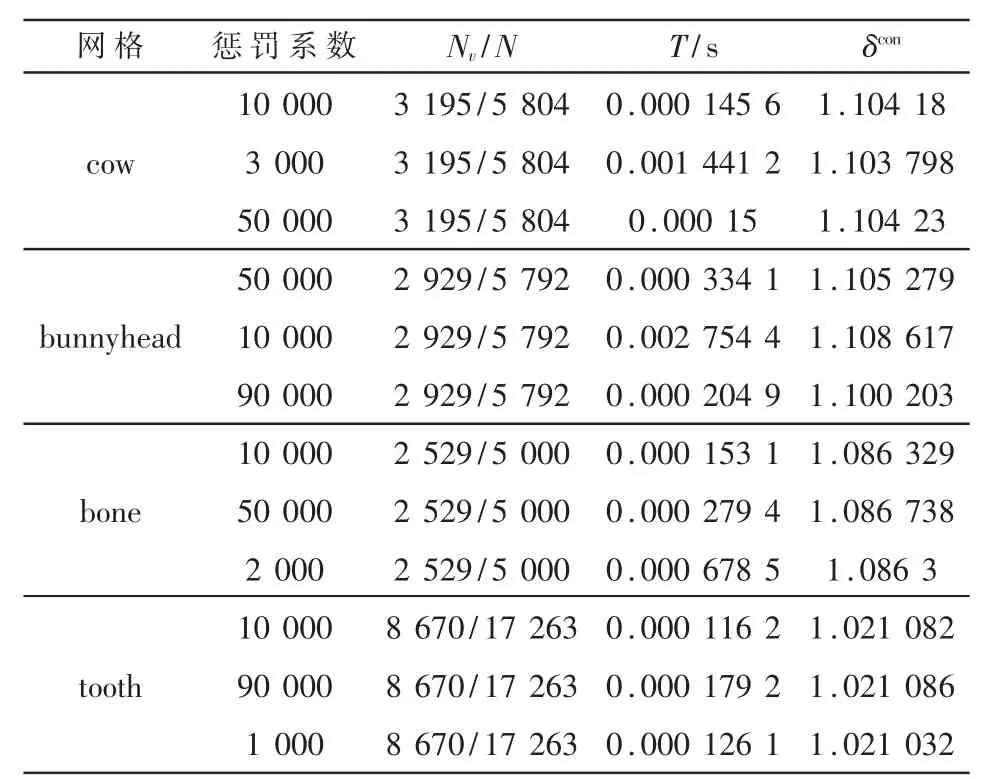
表3 不同惩罚系数比较

4 结论

随着参数化领域研究的发展，各种参数化算法被陆续提出。但快速产出无翻转、高质量的参数化映射一直是一个强烈需求。在本文中，提出一种针对于三角网格，计算三角网格的无翻转、高质量参数化结果的可并行、可扩展方法。该网格参数化ADMM算法可以高效并行地计算无翻转、高质量的三角网格映射，在处理大型网格上尤其占有优势。本文从不同角度、不同例子展示了该算法的优势。在处理大型网格或者希望快速处理网格时，都可以从该算法中得到益处。