无人机密集编队Backstepping控制器设计方法研究*

李继广，董彦非，屈高敏，岳 源，魏佳豪，唐家坤

(1 西安航空学院飞行器学院， 西安 710077； 2 西安航空学院通用航空工程技术中心， 西安 710071;3 中国民用航空飞行学院航空工程学院， 四川广汉 618307)

0 引言

目前，无人机编队飞行越来越受到普遍重视[1-3]。无人机编队可以克服单机功能单一、风险较大的缺陷，还可提高执行任务的效率，拓展使用范围。目前，美国正在大力实施微型无人机系统——单元可重组作战飞行阵列(SWARM)计划，用于构建未来无人机集群的监视、侦察、情报汇集和攻击等任务。编队飞行巨大的应用价值，受到了各国的高度重视，开展了一系列的工程开发研究，并即将进入实际部署应用阶段[4-7]。

无人机编队飞行面临着许多问题，如强耦合、非线性、鲁棒防碰撞的编队控制器设计等。为了解决这些问题，许多研究者做了大量的研究并取得了一些列成果。文献[8]基于Lyapunov方法设计了自适应控制器；文献[9]采用线性规划算法设计了编队保持的闭环控制器；文献[10]提出了一种基于多智能体系统技术的编队飞行智能优化控制方法；文献[11-12]应用Backstepping方法处理了机动飞行中的非线性问题并设计鲁棒控制器；文献[13]提出了一种多性能鲁棒控制器设计方法并证明了控制器的存在性。

这些研究成果从不同的理论方法出发，很好的解决了编队飞行中的非线性控制问题。然而，无人机密集编队飞行不仅要解决自身的非线性影响，还要解决编队间的气动耦合问题、各种干扰条件下的防碰撞鲁棒控制问题等。目前很多非线性鲁棒控制方法都要求系统不确定性范数是已知的。但是，该要求在复杂、大范围的飞行环境中是很难已知的。对于无人机密集编队飞行控制中的非线性、耦合特性和强鲁棒性需求，文中拟根据无人机密集编队飞行具体的动力学特性，采用一种改进的Backstepping控制方法加以解决。

1 无人机密集编队飞行模型

1.1 无人机二阶自动驾驶仪模型

为了精确反映编队飞行无人机的飞行品质，考虑到单架无人机机动飞行的延迟影响，采用二阶无人机自动驾驶仪模型。

(1)

式中：v、ψ、h分别为无人机飞行的速度、航向和高度；τv、τψa、τψb、τha、τhb是3个通道上的时间常数。

该二阶自动驾驶仪模型相较于一阶自动驾驶仪模型主要考虑了编队中个体的实际相应特性，使其航向和高度响应更加符合实际情况。在实际编队中，一般假定编队中的长机和僚机具有相同的飞行品质和机动性能，因此，编队中所有的无人机都可采用该二阶自动驾驶仪模型。为了后面编队控制器设计方便，将该模型表示成以下微分形式：

(2)

1.2 无人机编队运动模型

由式(2)可知，长机的自动驾驶仪模型为：

(3)

一般来说，松散编队飞行时，无人机编队间的气动藕合效应可以忽略不计。但是，密集编队飞行时，长机尾流会对僚机产生比较严重的耦合影响。该耦合响应就不得不考虑。根据风洞试验和相关有人机编队飞行的经验，长机尾流对僚机的耦合主要表现为对僚机的上洗流引起的上洗力。由于该上洗力的影响，僚机的迎角会发生变化，进而导致升力、阻力向量的旋转和大小改变。根据耦合因素产生的根源，其影响可表示为僚机升力L、阻力D、侧力Y的改变。

(4)

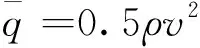
另外，长机和僚机间的相对距离也是决定编队间耦合效应影响强弱的关键因素之一。因此，在考虑长机和僚机间距影响下，对僚机的自动驾驶仪模型可表示为：

(5)

式中：x、y、z是编队间隔相对额定间隔x0、y0、z0的扰动量。

另外，长机和僚机间的相对运动学方程可表示为：

(6)

对于式(3)、式(5)、式(6),可得如式(7)所示仿射非线性方程的形式：

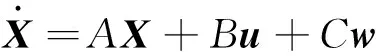
(7)

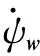
2 无人机编队飞行控制器设计

2.1 无人机编队控制策略分析

从上节建立的无人机密集编队飞行模型可知，该运动模型主要有长机的自动驾驶仪模型(式(3))、僚机的自动驾驶模型(式(5))和长机和僚机间的相对运动学模型(式(6))组成。从式(5)、式(6)可知，长机的下洗流会对僚机以及整个编队的保持产生重大的影响，即编队间的耦合影响。另外，从式(5)、式(6)可知，编队运动模型本身具有比较强烈的非线性。另外，为了更好的适应任务需求，编队整体应具有一定的机动能力。这就要求编队整体具有一定的稳定性、快速响应、航路精确跟踪的能力。同时，编队飞行过程中，各种扰动和外界干扰也会对无人机编队飞行产生影响，从而影响编队飞行稳定和航迹跟踪精度。所以，对控制器的鲁棒性也有较高的要求。对于各种扰动和外界干扰，控制器设计过程一般将其作为不确定性项加以处理。

因此，对于无人机编队控制来说，对控制器的要求包括稳定性、快速响应、稳态误差小以及较强的鲁棒性。为了保证编队飞行的安全，在编队控制器设计时应充分考虑这些实际需求。

对于无人机编队飞行来说，长机的飞行完全独立于僚机，而且长机发出的指令引导着整个编队的飞行，而僚机的控制指令则来源于编队控制器根据长机飞行指令解算得到的飞行指令。因此，无人机编队飞行控制器的整体结构如图1所示。

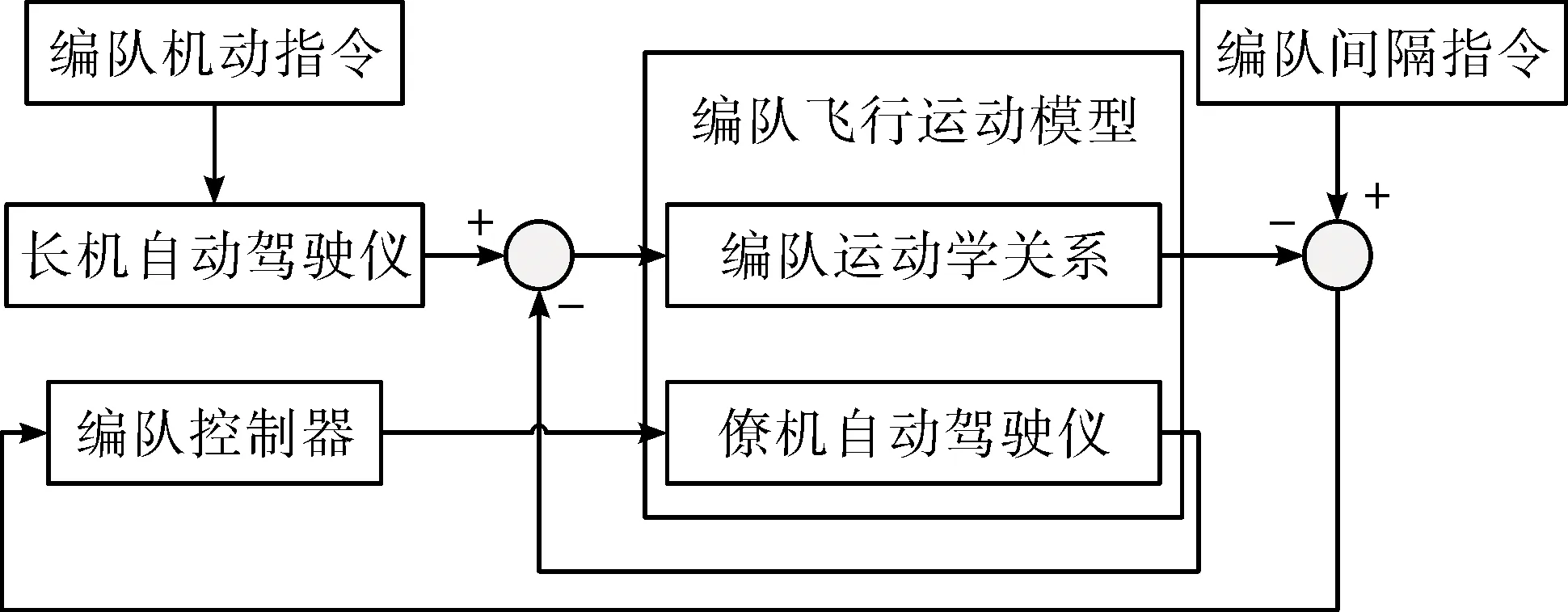
图1 无人机编队飞行控制器结构

2.2 无人机编队模型解耦处理

从式(7)无人机编队飞行仿射非线性模型可知，该模型为7阶。对7阶系统来说，无论采用何种设计方法计算都是十分巨大的。因此，有必要对该运动模型做进一步的处理。

虽然无人机编队飞行运动模型整体上呈现各通道间存在比较强的耦合性。但是，这种通道间耦合影响的强弱是不一样的。仔细分析式(7)可知，编队运动的高度通道和纵向通道间是不存在耦合影响的，也即这两个通道间可以实现完全解耦。而且侧向通道与纵向通道间的耦合也不严重，这种耦合影响仅发生在纵向通道的航向角速率之间。因此，可以利用无人机编队飞行运动模型这种自然的解耦关系，为控制器设计进行简化解耦处理。

根据无人机编队运动模型间自然的解耦关系，可以把无人机编队按照如下方式划分为3组：

(8)

根据该解耦关系，无人机编队飞行侧向通道的运动模型可表示为：

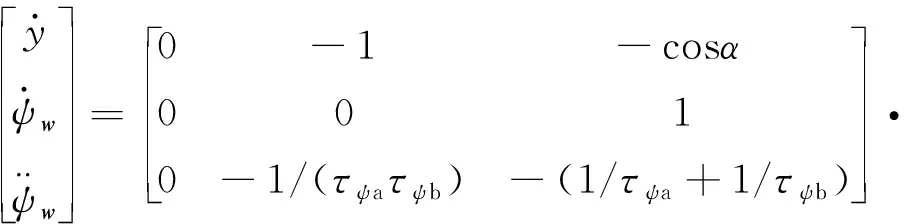
(9)

式(9)并不是严格的仿射非线性系统，为了形式上的统一，将该式变换为式(10)、式(11)两组方程：

(10)

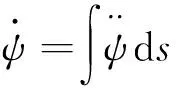
(11)

由于高度通道完全解耦，则解耦的高度通道运动模型可表示为：

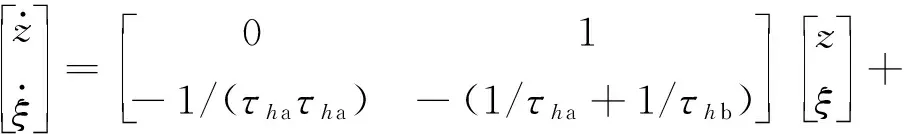
(12)

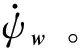
(13)

根据该通道解耦过程可得，无人机编队控制器设计步骤如下：

1)首先对侧向通道和高度通道进行控制器设计；

2)然后根据设计结果，将控制器加入到编队系统之后再对纵向通道进行设计。

这种各个通道分别设计的方式，不仅可以保证控制器的存在性，又可以降低控制器设计过程中的难度。

3 控制器设计

3.1 控制模型统一化

分别对式(10)、式(12)、式(13)所建立的仿射非线性模型进行控制器设计。具体设计过程要考虑各种扰动和外界干扰所带来的随机扰动和建模过程中所带来的摄动影响。因此，把以上格式统一表示如下：

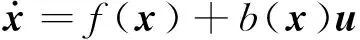
(14)

为保证控制器的鲁棒性，这里把上述模型表示为包含有不确定性的摄动模型：

f(x)=f0(x)+Δf(x)，b(x)=b0(x)+Δb(x)

式中：f0(x)、b0(x)为系统的标称参数，其余是系统的不确定项。

3.2 控制器设计和稳定性分析

无人机密集编队鲁棒自适应控制器设计的目的是在各种有界不确定性条件下，使得系统的状态收敛到指定信号任一无穷小的邻域内。因此，这里引入z的误差量：

z=x-xd

(15)

式中：xd为期望的系统状态轨迹。由式(14)可得误差状态的动态方程为：

(16)

对于该控制系统，总存在以下引理：

引理1[17]：存在正常实数xm使得b(x)对所有满足条件|x|≤xm的系统状态可逆。

对于式(16)所确定的系统，其摄动模型为：

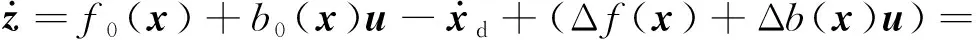
(17)

式中：Δ1=Δf(x)+Δb(x)u是系统的不确定项，即需要通过引入不确定函数进行补偿的部分。

假设存在一未知的正实数ρ1使得

‖Δ1‖≤ρ1δ1(x)

(18)

式中：δ1(x)为已知的非负光滑函数。

根据引理1可知，存在一个理想的虚拟控制量

(19)

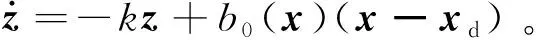
由于不知道u*的具体形式，这里选取以下理想的虚拟控制量。

(20)

式中：η1为需要设计的鲁棒函数系数，用来抵消不确定性Δ1的影响。

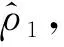
(21)

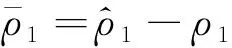
(22)

将式(20)所确定的u*代入式(22)可得:

(23)

选择自适应调节律

(24)

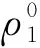
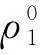
(25)

选择鲁棒函数系数η1和函数l1如式(26)、式(27)所示。

(26)

(27)

式中：ε1>0是需要的设计参数。

(28)

将式(26)和式(27)代入式(25)可得：

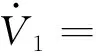
(29)

因为:

(30)

所以有:

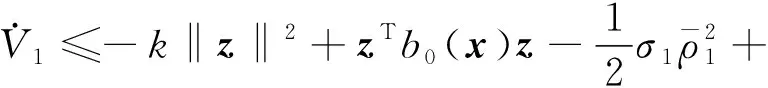
(31)

根据李雅普诺夫稳定性定理，系统是稳定的。

通过以上证明过程，可得如下结论：

对于由式(14)所确定的系统，采用式(20)所确定的控制量，以及式(26)所确定的自适应系数，则系统的跟踪误差z和参数估计误差有界且以指数形式收敛于系统原点的一个邻域内。

文中所提出的方法避免了许多鲁棒设计方法对系统不确定性范数上界已知的要求。同时，本方法采用鲁棒自适应函数来消除系统的不确定性，无需矩阵逼近控制方法引起的控制奇异问题。

4 仿真验证

无人机编队飞行，僚机主要跟踪长机的航向、速度和高度指令，从而实现跟随长机进行机动的编队飞行目标，并在机动过程中保持编队间隔不变。根据图1所示的控制结构，以及上文所介绍的编队控制器设计方法，对无人机编队飞行控制效果进行仿真验证。编队初始飞行条件为：航向角ψ0=0o，飞行高度h0=900 m，编队速度v0=135 m/s；编队间隔分别为x0=18 m，y0=7 m，z0=0 m。同时为了验证控制器的鲁棒性能，仿真过程给僚机的升力系数添加±20%的随机扰动。在该初始编队飞行条件下，编队采取航向角ψc=20o机动指令，采用文中设计方法得到的控制器控制效果如图2～图4所示。

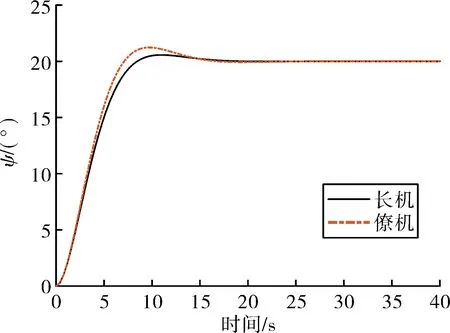
图2 编队航向角机动响应

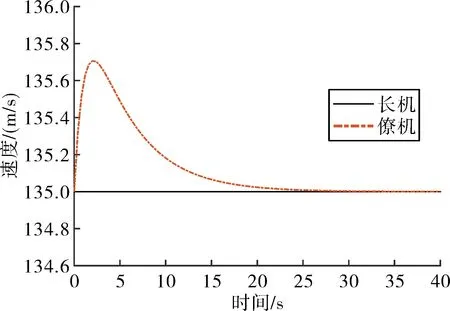
图3 编队航向角机动时的速度响应

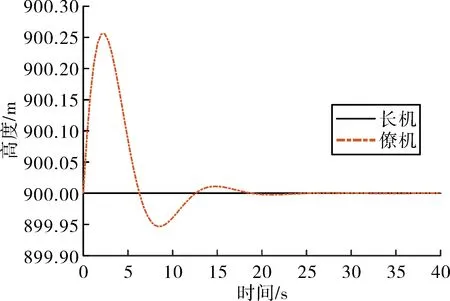
图4 编队航向角机动时的高度响应

从仿真结果可知，编队僚机迅速跟上了长机的航向角机动指令，并且无误差。在航向角机动过程中，编队中僚机的速度最大偏差仅为0.7 m/s,高度偏差最大仅为0.20 m。

在机动飞行过程中，对于侧向通道的控制，其目的主要是使系统能精确的跟踪长机发出的航向角指令，并按照编队间距要求保持僚机参考系中y方向间距不变；对于高度通道的控制，其目的主要是按照编队高度间距要求保持僚机参考系中z方向间距不变；对于纵向通道的控制，其目的主要是使系统能精确的跟踪长机发出的速度指令，并按照编队间距要求保持在僚机参考系中x方向间距不变。编队航向角机动时的三通道的响应如图5～图7所示。

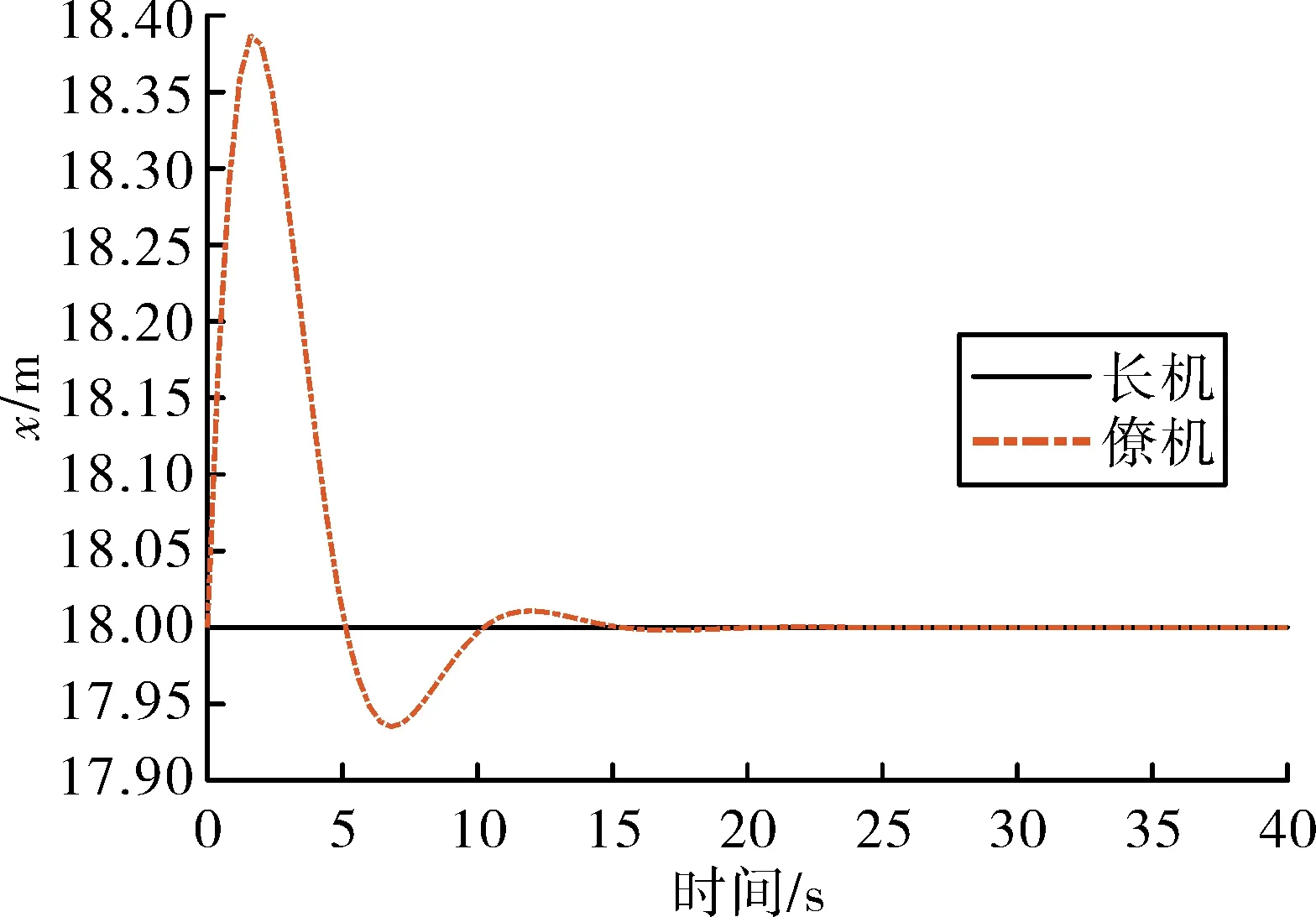
图5 编队航向角机动时的纵向通道响应

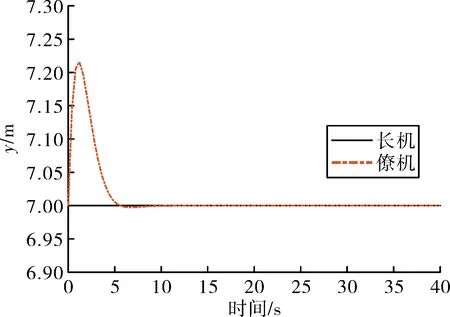
图6 编队航向角机动时的侧向通道响应

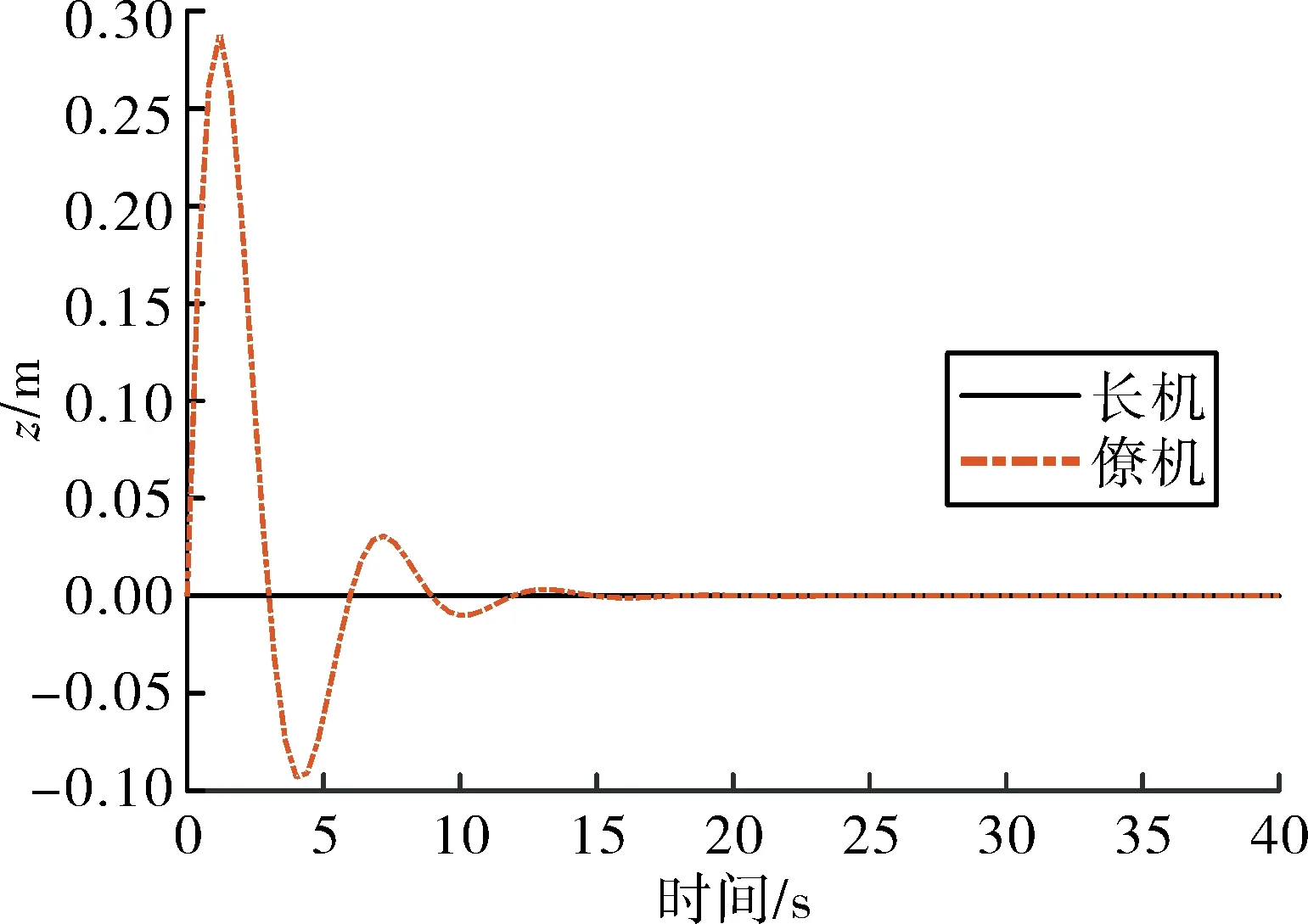
图7 编队航向角机动时的高度通道响应

在机动过程中，编队的间隔保持良好，最大航向距离偏差为0.38 m，最大侧向偏差为0.22 m。僚机的高度误差出现轻微震荡，但最终得到了消除。高度间隔的震荡主要是由编队间非线性耦合所引起的。

从仿真可知，所提方法设计得到的无人机编队控制器具有较好的效果。

5 结论

针对无人机编队飞行控制，文中做了以下几方面的工作：

1)针对编队飞行控制的需求，建立了无人机编队飞行动力学模型。

2)针对无人机编队飞行控制器设计控制器参数存在性问题和设计过程复杂等问题，提出了编队运动方程解耦方法并提出了单通道设计的思路。

3)针对编队飞行强非线性、强耦合特性和强鲁棒性的实际需求，提出一种改进Backstepping控制方法，并证明了该控制器的稳定性。

文中所提控制思路和方法满足了无人机编队飞行的实际需求，降低了设计难度，而且避免了很多鲁棒非线性设计方法对系统不确定性已知的限制。仿真结果显示，该设计方法是有效的。