履带式战车行进间发射导弹出筒姿态研究*

胡 东，姜 毅，刘 伟，赵若男

(北京理工大学宇航学院， 北京 100081)

0 引言

随着军事科技的发展，空袭正变得多样化和隐形化，防空成为了具有广泛战略意义的军事行动[1]，具有行进间发射能力的武器系统是一个重要研究方向。履带车辆具有极好的机动性和通过性，以其作为运输载体，能够大幅提高武器系统作战能力。

行进间发射过程中，路面质量和车速等因素都会引起导弹出筒姿态的变化，影响发射精度。研究行进间发射问题具有一定的理论意义和工程应用价值，能够为行进间发射武器系统的设计、验证和优化提供参考。我国一些学者做了初步探索，并取得了较为丰富的成果[2-7]。

文中以某型履带式战车为具体对象，建立了多刚体动力学模型，并基于傅里叶逆变换法建立了高精度路面模型，借助计算机仿真对导弹出筒姿态进行了研究。考虑到路面不平度激励的随机性，采用了直方图法和方差分析法[8]，从统计学角度出发，进一步研究了路面等级和车速对行进间发射导弹出筒姿态的影响程度和规律，同时给出了行进间发射安全性评估的方法。

1 行进间发射动力学模型

1.1 路面模型

国家标准GB/T 7031—2005中，采用垂直位移的单边功率谱密度来拟合路面不平度：

(1)

式中：Ω为空间频率，单位为m-1；Ω0为参考空间频率，大小为0.1 m-1；S(Ω0)为参考空间频率下的功率谱密度值；ω为频率指数，取值为2；(Ω1,Ω2)为有效空间频率范围，一般取值为(0.011 m-1,2.83 m-1)。

基于IFFT法进行路面不平度模拟，得到路面不平度离散数据为：

(2)

式中：N为离散份数；S(Ωk)为功率谱密度函数在(Ω1,Ω2)内的离散采样值；φk为相位角，是[0，2π]内的随机数。

通过编写程序模拟长度为100 m的路面，各等级路面不平度几何平均值σ的国标参考值和模拟值如表1所示，两者十分接近。图1以B级路面为例给出了路面不平度曲线。

表1 路面不平度的几何平均值

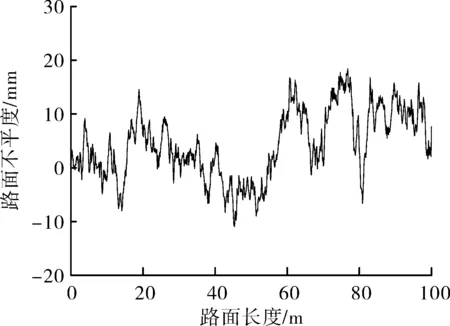
图1 B级路面不平度曲线

1.2 车体模型

履带式战车根据各个部件功能关系可分为车体、车载设备和发射装置三大部分，如图2所示。模型坐标系的x轴方向为车辆前进方向，y轴方向垂直于地面向上，z轴方向通过右手定则确定。

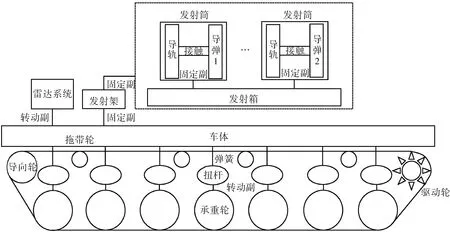
图2 履带式战车拓扑连接图

导弹采用垂直发射，定义导弹分别绕x、y和z轴的角位移为俯仰角位移θx、滚转角位移θy和偏航角位移θz，分别绕x、y和z轴转动的角速度为俯仰角速度ωx、滚转角速度ωy和偏航角速度ωz。

履带式战车行进间发射过程中力学环境十分复杂，为了描述武器系统在行进间发射时的动力学特性，特作如下假设：

假设1：不考虑连接铰间隙，均设为理想约束；

假设2：不考虑零部件变形，整个模型为刚体；

假设3：履带与地面之间为刚性接触；

假设4：悬挂系统用等效弹簧阻尼模型模拟；

假设5：不考虑发射过程中导弹的变质量特性。

1.3 激励载荷

导弹在弹射装置提供的弹射力作用下运动，采用随体单向力进行模拟，作用点位于提弹梁质心，方向近似平行于导轨。图3给出了弹射力随时间变化曲线。

图3 弹射力曲线

2 计算机仿真与结果分析

2.1 样本数据获取

通过编写程序生成批处理文件(.bat)和求解控制文件(.rss)，以发射时刻t为设计变量进行批处理仿真，获取不同工况下大量样本数据。仿真控制流程如图4所示。

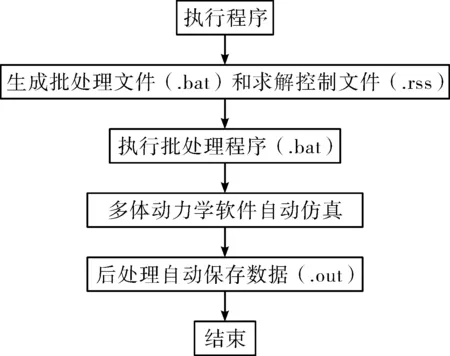
图4 仿真控制流程图

由于弹筒结构和装配特征会直接影响导弹滚动姿态，所以选取决定导弹起控精度的俯仰方向和偏航方向初始扰动为研究对象。受篇幅所限，文中并未罗列全部仿真结果，仅以导弹出筒俯仰角位移θx和角速度ωx为例进行分析。

2.2 样本数据处理

采用直方图法对样本数据进行处理，将N个样本数据分为k组，确定组距Δ、组限及各组中间值ti。组数k由以下经验公式确定：

k=1+3.32lgN

(3)

统计各组的频数ni，计算各组的频率fi为：

fi=ni/N

(4)

(5)

以ti为横坐标，fi/Δ为纵坐标绘制频率直方图，当样本容量N足够大，组距Δ足够小时，频率接近概率，直方中点的连线可表示总体的概率密度曲线。

2.3 导弹出筒姿态分布规律研究

图5～图6为一种计算工况下(C级路面，20 km/h车速)不同发射时刻导弹出筒瞬间俯仰角位移θx和角速度ωx的样本数据。由图5～图6可得，俯仰角位移θx和角速度ωx随着发射时刻(发射位置)的改变呈现随机变化。

图5 俯仰角位移样本数据

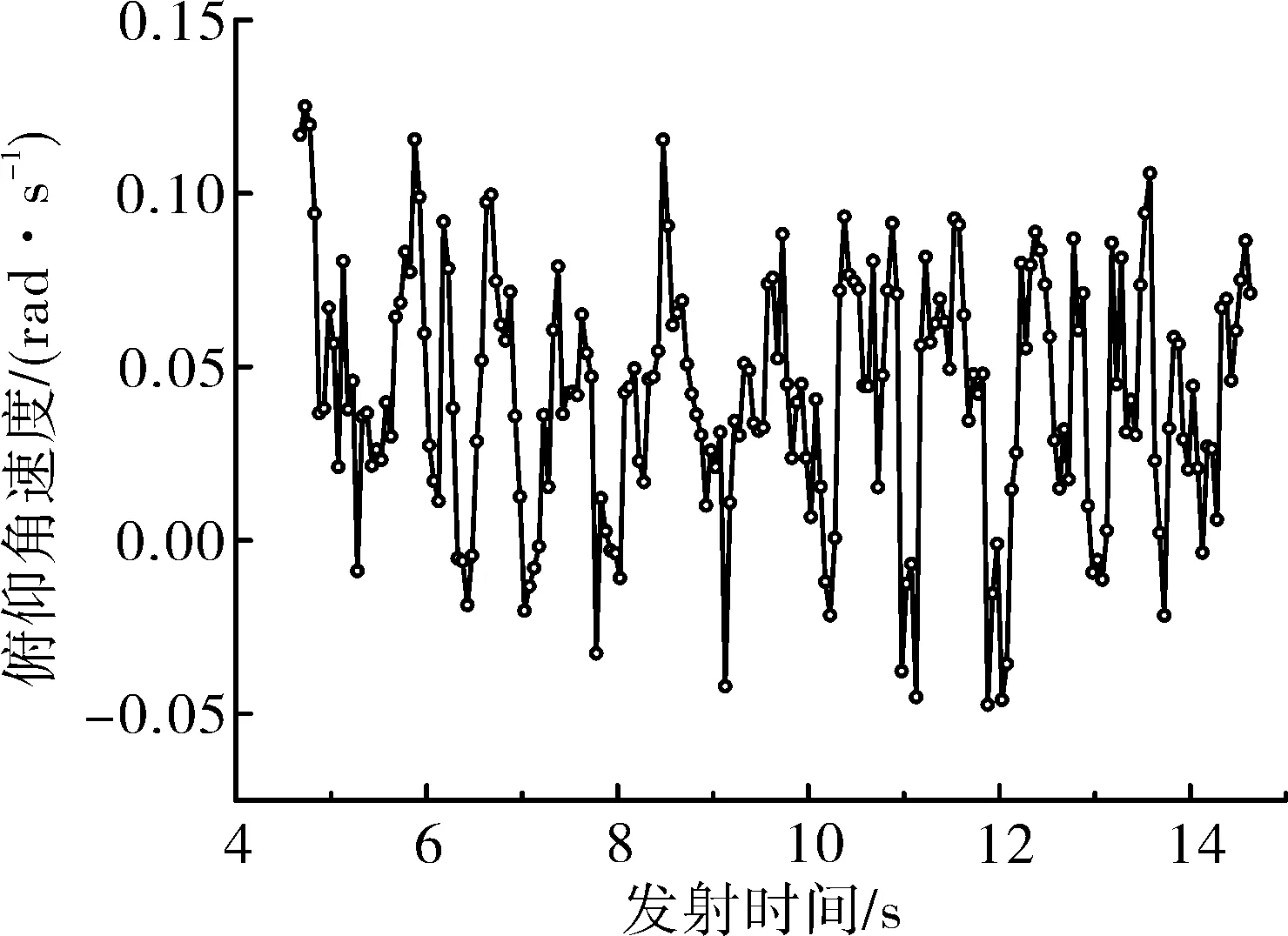
图6 俯仰角速度样本数据

采用直方图法对导弹出筒姿态样本数据进行处理，图7～图8给出了俯仰角位移θx和角速度ωx的频率直方图。由图7～图8可得，在随机路面不平度的扰动下，俯仰角位移θx和角速度ωx样本数据的频率直方图近似于正态分布图形。采用极大似然估计法[8]对其概率密度函数进行参数估计，估计结果如表2所示。

图7 俯仰角位移频率直方图

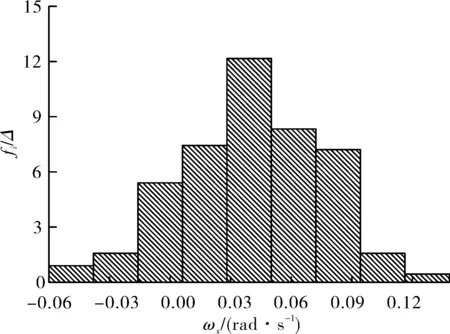
图8 俯仰角速度频率直方图

表2 均值和方差估计结果

以俯仰角位移θx为例，图9给出了估计而得的正态分布概率密度曲线与导弹出筒姿态样本数据频率直方图的对比。

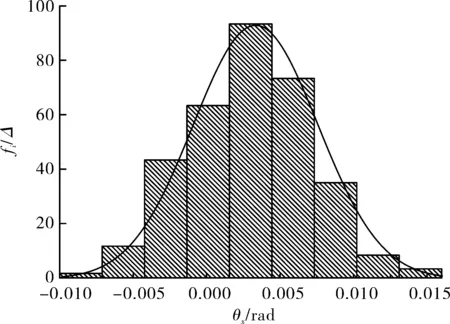
图9 概率密度曲线与频率直方图对比图

综上所述，履带式战车行进间发射过程中，由于受到随机路面不平度的扰动，导弹出筒俯仰角位移θx和角速度ωx服从正态分布。

3 导弹出筒姿态影响因素分析

3.1 双因素等重复试验的方差分析

设因素A、B作用下的样本Xijk服从正态分布，其中因素A有r个水平A1、A2、…、Ar，因素B有s个水平B1、B2、…、Bs，Xijk相互独立，为水平组合(Ai,Bj)作用下第k次试验样本。

引入总偏差平方和：

ST=SE+SA+SB+SA×B

(6)

式中：ST为总偏差平方和；SE为误差平方和；SA和SB分别为因素A、B的效应平方和；SA×B为因素A、B交互效应平方和。其自由度依次为：rst-1、rs(t-1)、r-1、s-1和(r-1)(s-1)，且满足等式：

式中：

(8)

处理均值之间没有差异时：

(9)

取显著性水平为α，若FA≥Fα(r-1,rs(t-1))，则因素A的影响是显著的；若FB≥Fα(s-1,rs(t-1))，则因素B的影响是显著的；若F(A×B)≥Fα((r-1)(s-1),rs(t-1))，则因素A和B的交互作用效应是显著的。反之则为不显著。

3.2 试验设计

履带式战车行进间发射过程中，路面质量和车速是影响导弹出筒姿态的主要因素。因此，选择路面质量和车速作为试验因素。考虑客观实际，选择路面等级水平为B级、C级和D级；选择车速为20 km/h、30 km/h和40 km/h。针对每一种工况进行大量试验，以导弹出筒姿态的均方根值作为试验指标。

针对每一种工况做2次重复试验，每次试验进行200次仿真，并统计200个姿态数据的均方根值，表3～表4给出了俯仰角位移θx和角速度ωx的试验结果。

3.3 路面等级和车速的影响程度分析

对表3～表4中试验结果进行因素显著性检验,得到俯仰角位移θx和角速度ωx方差分析表如表5～表6所示。

表3 俯仰角位移均方根值试验结果 rad

表4 俯仰角速度均方根值试验结果 rad/s

显著性水平α=0.005时，F0.005(2,9)=10.1，F0.005(4,9)=7.96。由表5～表6可得：F比数值365.45、162.11、217.74和113.72都大于F0.005(2,9)：F比数值32.13和21.50都大于F0.005(4,9)。由此可以得到以下结论：

表5 俯仰角位移均方根值方差分析表

表6 俯仰角速度均方根值方差分析表

路面等级对导弹出筒俯仰角位移θx和角速度ωx的影响是显著的；车速对导弹出筒俯仰角位移θx和角速度ωx的影响是显著的；路面等级和车速的交互作用效应是显著的。

3.4 路面等级和车速的影响规律分析

根据表3～表4计算各因素在每个水平下的试验指标平均值，绘制相应的因素-指标趋势图[9]，对于同一因素，直线斜率反映了该因素水平变化区间对试验指标的影响趋势。试验指标平均值计算结果如表7～表8所示。

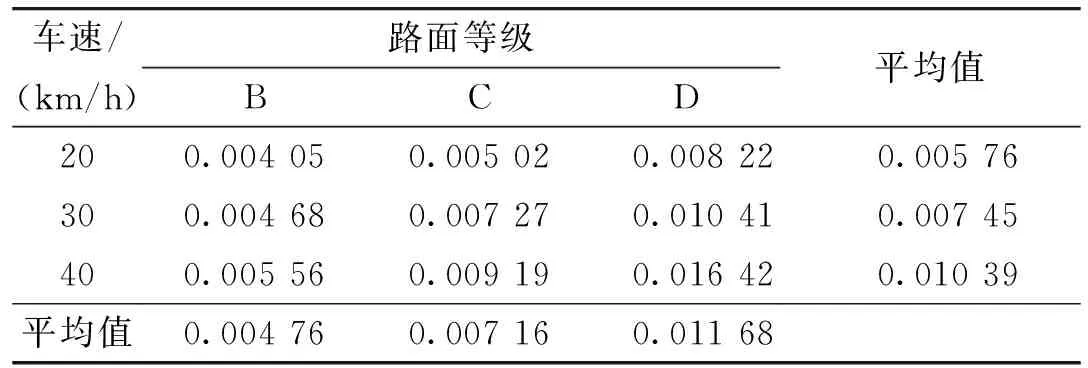
表7 俯仰角位移均方根值平均值 rad

根据表7～表8中计算结果，图10～图11给出了俯仰角位移θx和角速度ωx均方根值的因素-指标趋势图。

表8 俯仰角速度均方根值平均值 rad/s

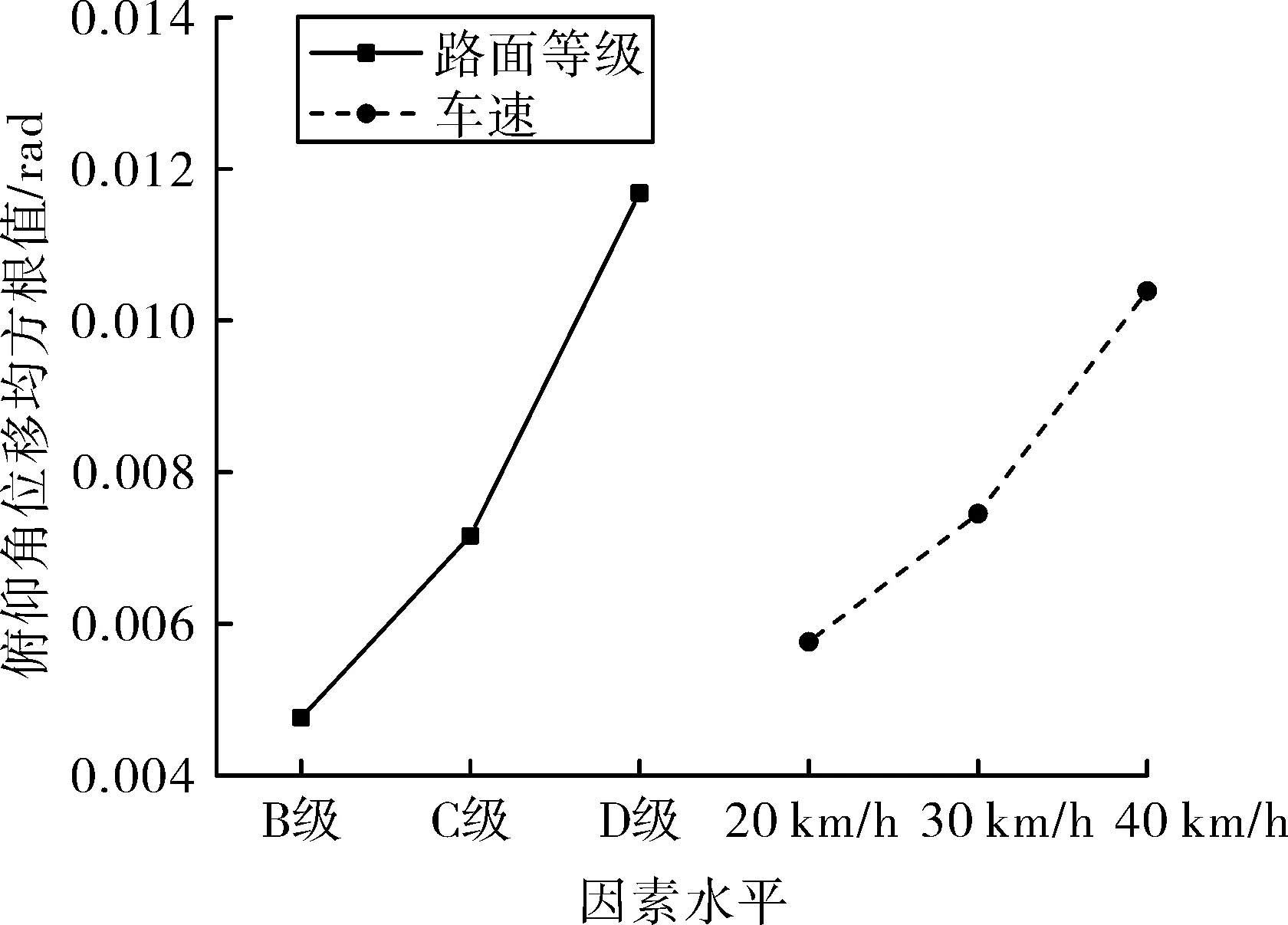
图10 俯仰角位移均方根值因素-指标趋势图

图11 俯仰角速度均方根值因素-指标趋势图

由图10和图11可得，路面从B级到D级，俯仰角位移θx和角速度ωx均方根值的平均值变化曲线单调递增，且斜率增大，车速从20 km/h到40 km/h具有类似的规律。由此可以得到以下结论：

随着路面质量逐渐变坏，导弹出筒俯仰角位移θx和角速度ωx都增加，且增长趋势都逐渐加快;随着车速逐渐变快，导弹出筒俯仰角位移θx和角速度ωx都增加，且增长趋势都逐渐加快。

3.5 行进间发射安全性评估

履带式战车行进间发射过程中，导弹出筒俯仰角位移θx和角速度ωx服从正态分布。根据“3σ”原则，俯仰角位移θx和角速度ωx落在(μ-3σ，μ+3σ)区间内的概率都为99.74%。以路面等级为C级，车速为20 km/h计算工况为例进行评估分析，表9给出了该工况下的相应区间。

表9 区间计算结果

根据表9中计算结果，认为C级路面，20 km/h车速下俯仰角位移θx<0.015 4 rad的概率为99.74%，俯仰角速度ωx<0.148 7 rad/s的概率为99.74%。该型履带式战车导弹出筒姿态起控精度要求为角位移<0.3 rad，角速度<0.3 rad/s，试验结果表明偏航角位移θz和角速度ωz所在区间最大数值都小于0.3。因此，认为该型履带式战车在C级路面，20 km/h车速下发射导弹是安全的。

4 结论

基于IFFT法，完成了高精度的路面不平度模拟。基于多体动力学理论，建立了履带式战车动力学模型。编写程序实现自动仿真，获取了导弹出筒姿态的大量试验样本数据。

基于直方图法对样本数据进行分析，得到了结论：随机路面不平度扰动下，履带式战车行进间发射导弹出筒姿态呈正态分布。采用极大似然估计法得到了均值和方差估计值，同时给出了行进间发射安全性评估的方法。

基于双因素等重复试验方差分析法及因素-指标趋势图分析法研究了路面等级和车速对行进间发射导弹出筒姿态的影响程度和规律，得到了结论：路面质量和车速对导弹出筒姿态都会产生显著影响，且两者交互作用效应也是显著的。随着路面质量变差或车速变快，导弹出筒姿态增加,且增长趋势增大。