旋转载体圆锥姿态解算方法研究*

张双彪，李兴城

(1 北京信息科技大学高动态导航技术北京市重点实验室, 北京 100101; 2 北京理工大学宇航学院, 北京 100081)

0 引言

火箭弹、制导炮弹、制导子弹等旋转载体常采用的姿态解算方法是以欧拉角为基础的，如欧拉角姿态解算方法和基于旋转矢量的双步姿态解算方法，前者常用于控制系统设计，后者常用于定位、定向和导航系统，但两种方法均受锥形运动影响而出现不同程度的姿态解算误差[1-2]，因此姿态解算得到了国内外广大学者的关注。研究发现，旋转载体的锥形运动存在两种旋转方式，一种是通过绕3个正交轴旋转表征的形式，如图1所示；另一种是载体因定轴转动而发生的章动和进动表现的双轴旋转形式，如图2所示[3-4]。两种锥形运动均会影响姿态解算方法，特别是自转姿态误差发散严重。为提高姿态解算的适应性和解算精度，广大学者主要采用便于参数优化的双步姿态解算方法，通过锥形运动条件优化旋转矢量的计算参数，抑制姿态误差，并利用旋转矢量计算姿态矩阵，得到载体姿态，而优化效果凭借误差漂移率体现[5-9]。然而，目前该类姿态误差并未得到有效消除。

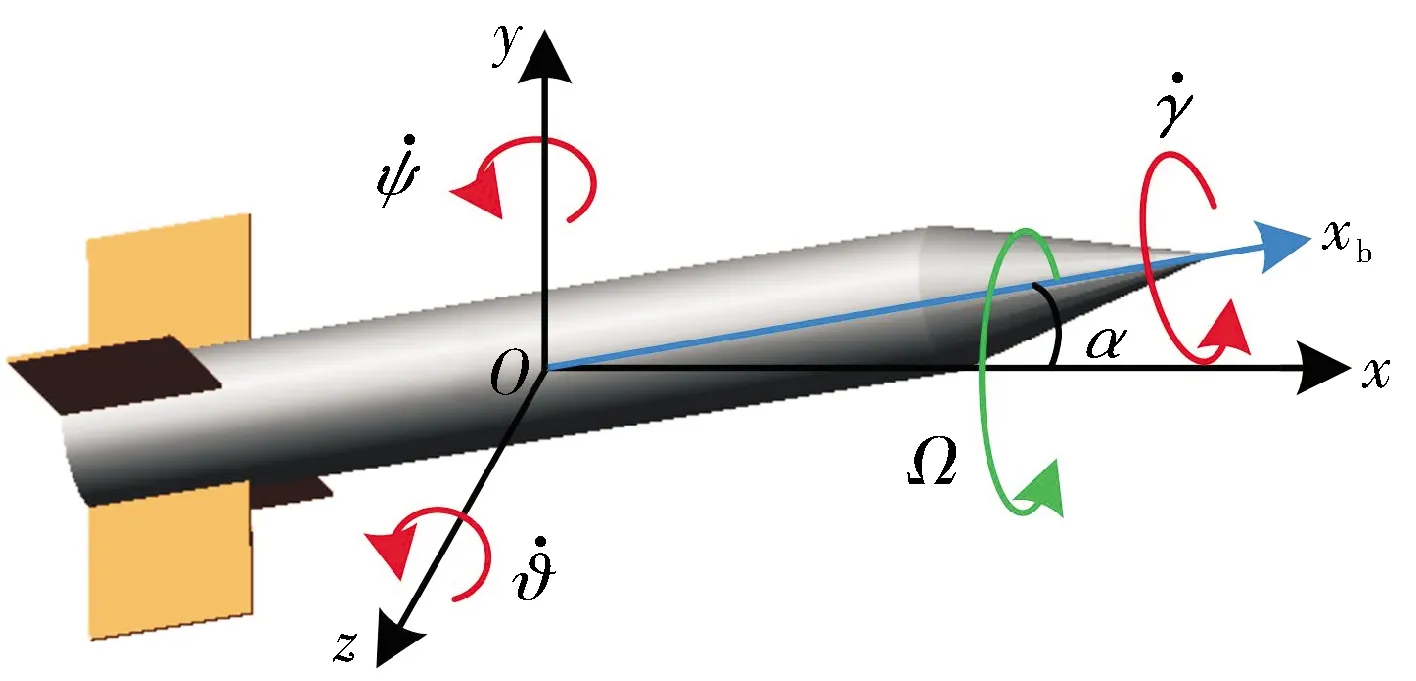
图1 三轴旋转表征的锥形运动

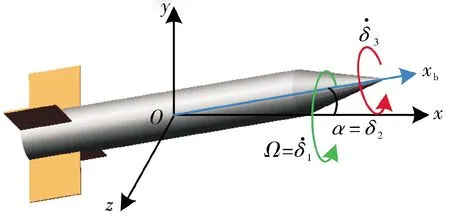
图2 两轴旋转表征的锥形运动

为此，提出圆锥姿态解算方法，并给出基于旋转矢量的双步姿态解算过程，通过与传统的解算方法进行仿真对比，证明该方法的优越性。

1 常规的姿态解算方法

1.1 欧拉角姿态解算方法

欧拉角姿态解算方法是传统的姿态解算方法，根据飞行力学知识，载体的角运动模型为[10]：

(1)

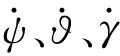
(2)

利用获得的角速度测量值，可以解算载体姿态。由欧拉角表示的载体坐标系Oxbybzb到参考坐标系Oxyz的姿态矩阵为：

(3)

式中:上角标i表示目标坐标系为参考坐标系;C11=cos(ϑ)cos(ψ)；C12=-sin(ϑ)cos(ψ)cos(γ)+sin(ψ)sin(γ)；C13=sin(ϑ)cos(ψ)sin(γ)+sin(ψ)·cos(γ)；C21=sin(ϑ)；C22=cos(ϑ)cos(γ)；C23=-cos(ϑ)sin(γ)；C31=-cos(ϑ)sin(ψ)；C32=sin(ϑ)sin(ψ)cos(γ)+cos(ψ)sin(γ)；C33=-sin(ϑ)·sin(ψ)sin(γ)+cos(ψ)cos(γ)。

在锥形运动环境下，利用俯仰角ϑ和偏航角ψ可以近似计算半锥角：

(4)

1.2 双步姿态解算方法

双步姿态解算方法包括旋转矢量更新和姿态矩阵更新两个过程，具体更新如下[3]：

φl=αl+δφl

(5)

(6)

(7)

式中l表示第几次循环，为便于数据更新，式(7)常被近似为下式：

(8)

式中kij为旋转矢量优化参数。

姿态矩阵更新如下：

(9)

(10)

(11)

(12)

(13)

利用旋转矢量解算欧拉角时，俯仰角ϑ、偏航角ψ和滚转角γ分别利用下式计算：

(14)

(15)

(16)

偏航角ψ和滚转角γ真值根据表1和表2确定。

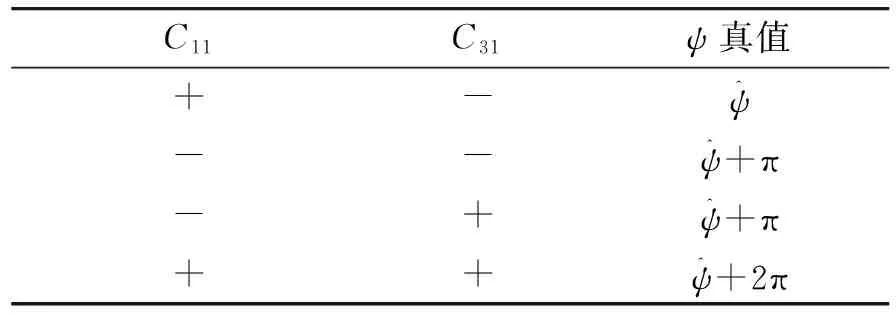
表1 ψ取值

2 圆锥姿态解算方法

圆锥姿态解算方法借鉴了章动原理，通过定义圆锥姿态角表述锥形运动，分别为进动角δ1，章动角δ2，自转角δ3，其中δ1取值范围为[0° 360°]，δ2取值范围为[0° 90°]，δ3取值范围为[0° 360°][8]。进动角表征锥形运动的旋转过程，章动角表征锥形运动的摇摆幅度，自转角则表征载体在进行锥形运动时自转过程，见图2。需要说明的是，当Oxbyb面位于铅垂面内时为进动角δ1起始位置。与章动原理不同的是，文中针对坐标系旋转过程进行了改进，具体为：

根据旋转顺序可以得到通过圆锥姿态角表示的参考坐标系Oxyz与载体坐标系Oxbybzb的旋转关系，如图3所示。

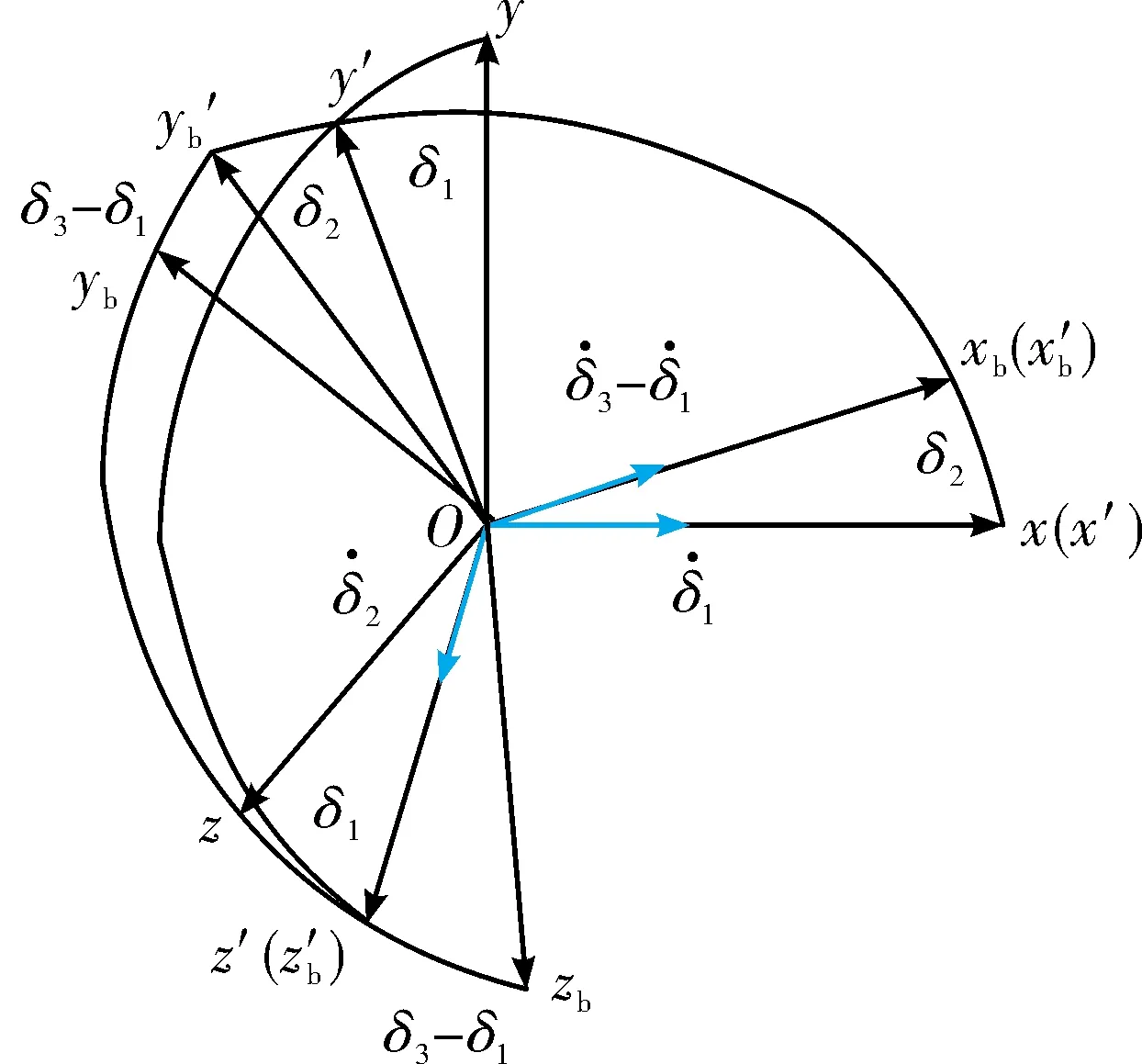
图3 锥形运动姿态角的两轴旋转过程

根据图3建立旋转载体的角运动方程为：

(17)

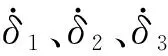
(18)

当δ2不为零时，根据式(18)可以利用角速度测量值实时解算锥形运动的姿态角。根据欧拉姿态角与圆锥姿态角的几何关系建立如下表达式：

ϑ=±arcsin|sinδ1sinδ2|

(19)

(20)

二者的符号可以根据表3和表4选取。

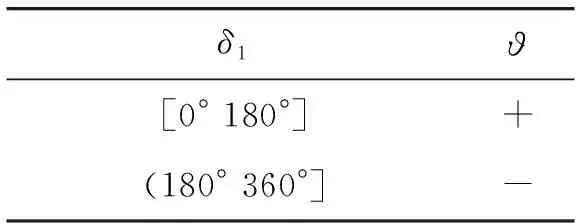
表3 ϑ符号选取

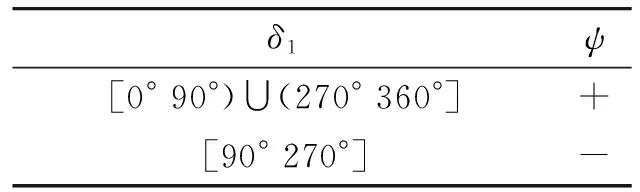
表4 ψ符号选取

由式(18)可知，当δ2为零时，存在奇异值的问题。为提高圆锥姿态适应性，同样可以利用双步姿态解算结构更新载体的圆锥姿态，见式(5)～式(10)，载体坐标系Oxbybzb到参考坐标系Oxyz的圆锥姿态矩阵可根据图3旋转关系确定，具体为：

(21)

式中:D11=cosδ2；D12=-cos(δ1-δ3)sinδ2；D13=-sin(δ1-δ3)sinδ2；D21=cosδ1sinδ2；D22=sin(δ1-δ3)sinδ1+cos(δ1-δ3)cosδ1cosδ2；D23=-cos(δ1-δ3)sinδ1+sin(δ1-δ3)cosδ1cosδ2;D31=sinδ1sinδ2；D32=-sin(δ1-δ3)cosδ1+cos(δ1-δ3)sinδ1cosδ2；D33=cos(δ1-δ3)cosδ1+sin(δ1-δ3)sinδ1cosδ2。

根据式(21)，可以建立圆锥姿态计算公式：

(22)

δ2=arccosD11

(23)

(24)

需要说明的是，自转角δ3是需要确定进动角δ1后再计算。进动角δ1和自转角δ3的真值可根据表5和表6所示确定。

表5 δ1取值

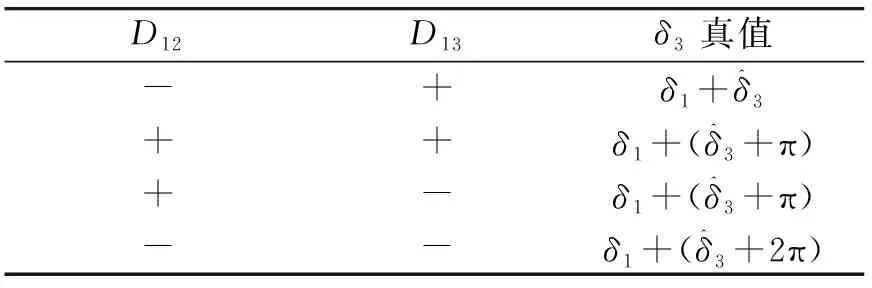
表6 δ3取值

3 仿真与分析

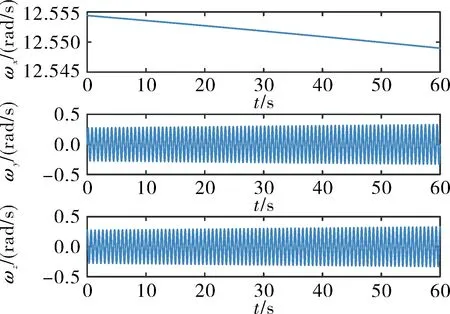
图4 角速度测量值

首先，将欧拉角姿态解算方法与双步姿态解算方法进行对比。图5为旋转矢量方法优化后欧拉角姿态误差，姿态角存在振荡式发散误差，误差量级为10-5～10-4rad。图6为旋转矢量方法优化前后的欧拉角姿态误差对比，误差表现为复杂的发散现象，量级为10-14～10-13rad。结合图5和图6，说明双轴旋转锥形运动引起的姿态发散振荡误差，在旋转矢量优化后仍然存在，优化效果并不明显，同时说明利用双步姿态解算方法得到欧拉角存在误差。

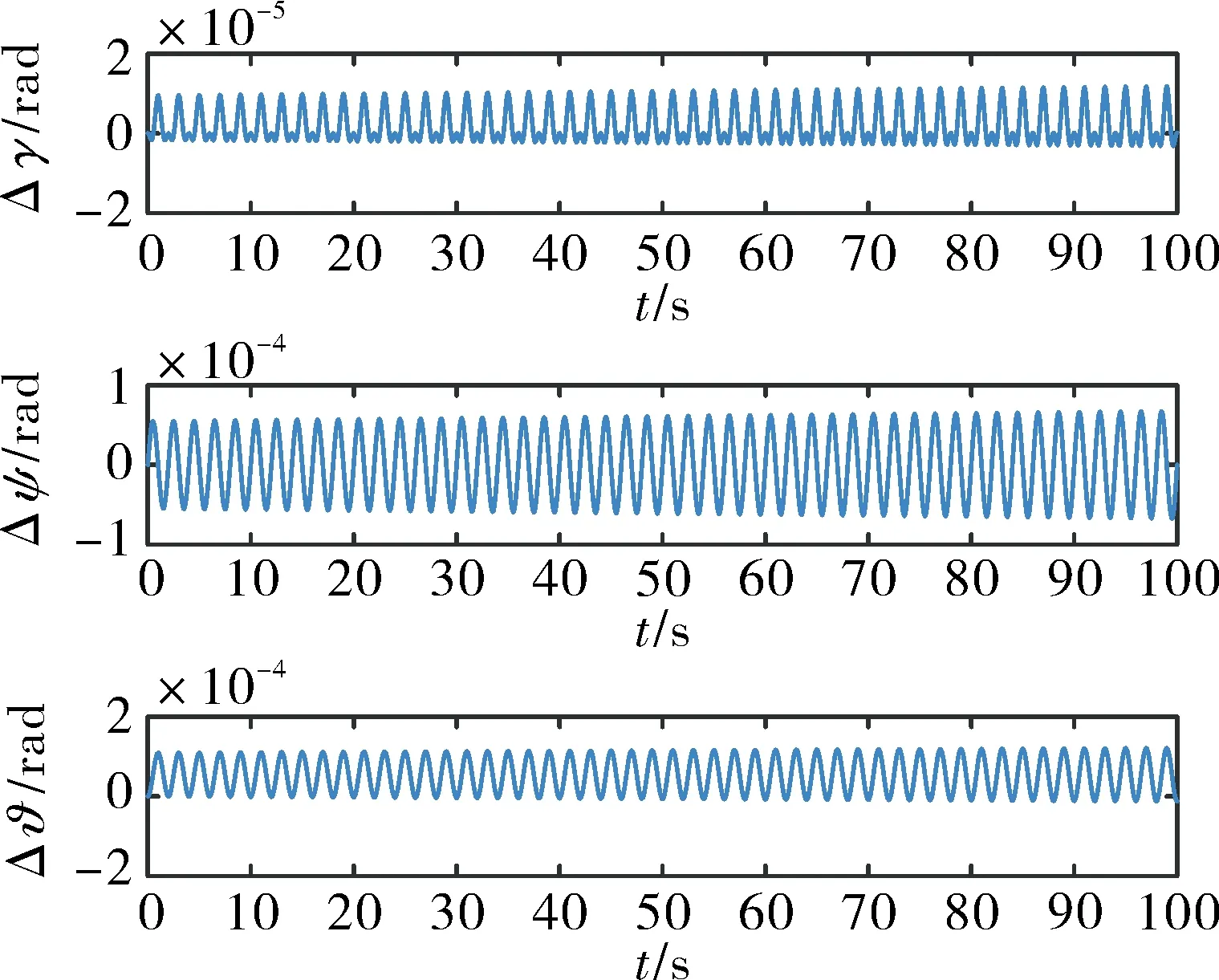
图5 旋转矢量方法优化后欧拉角姿态误差

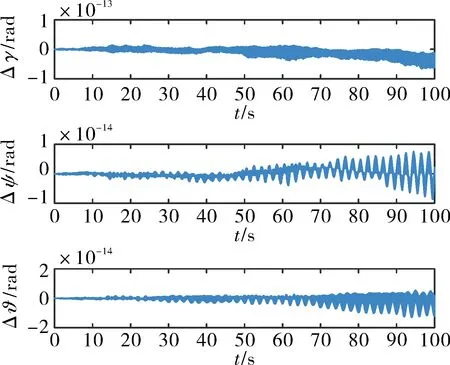
图6 旋转矢量方法优化前后的欧拉角姿态误差对比

然后，将圆锥姿态解算方法与双步姿态解算方法进行对比。图7为旋转矢量方法优化后圆锥姿态误差，可见仍存在振荡式误差，但并未发散，章动角δ2误差量级为10-5rad，自转角δ3的误差量级为10-6rad，精度均高于欧拉角姿态。图8为旋转矢量方法优化前后圆锥姿态误差对比，优化前后误差并未发散，误差量级为10-4～10-3rad，且自转角δ3精度未得到提高。分析图7和图8可知，旋转矢量方法的优化与否对圆锥姿态自转角的影响并不明显，同时也证明双步姿态解算方法存在误差。

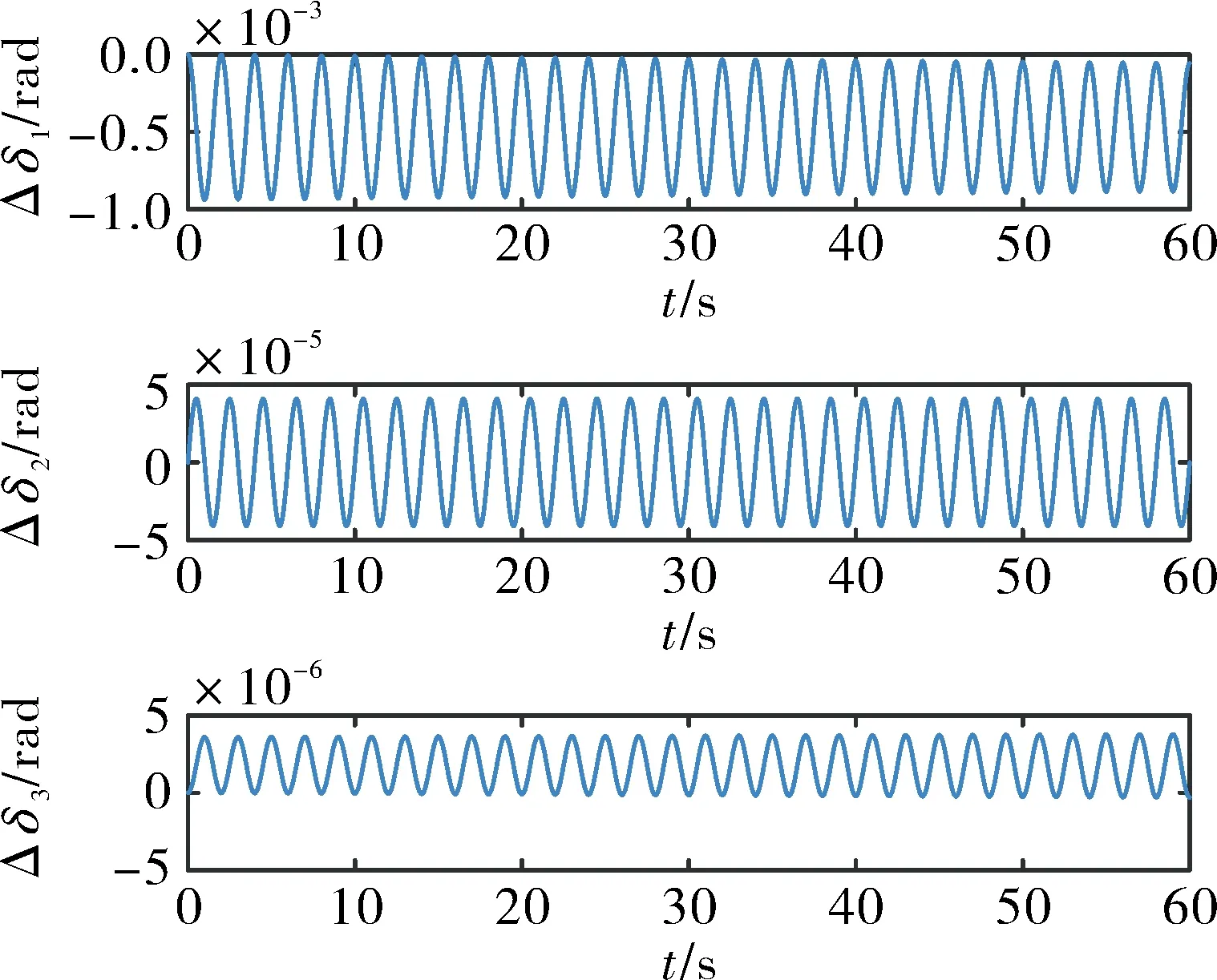
图7 圆锥姿态解算方法与旋转矢量对比

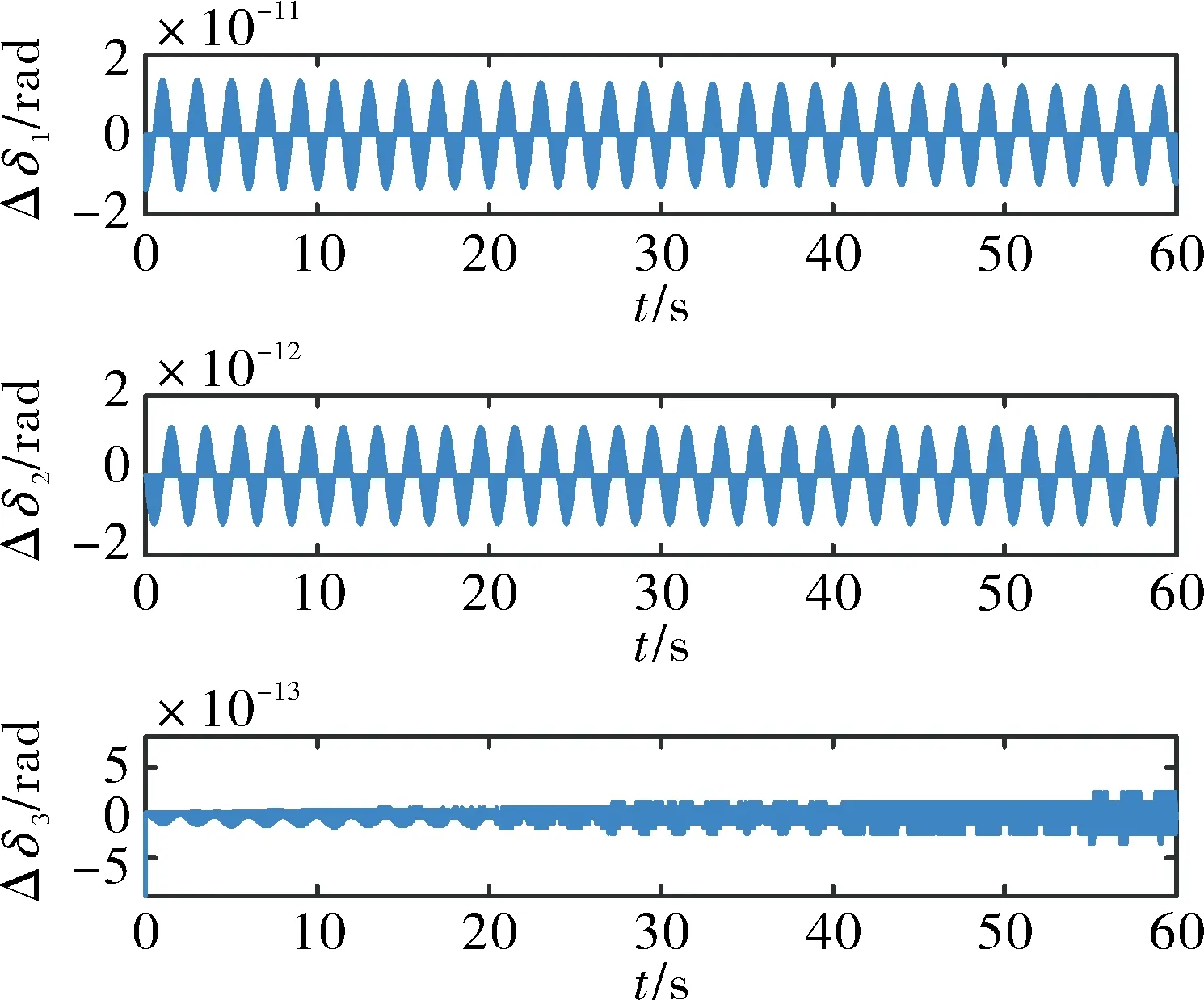
图8 旋转矢量方法优化前后的圆锥姿态误差对比

最后，分别利用基于欧拉角姿态的解算方法与基于圆锥姿态的解算方法计算半锥角α，并进行对比。如图9所示，欧拉角姿态计算存在发散的误差，圆锥姿态解算方法无误差，但其双步姿态解算方法存在不发散的振荡误差，具体误差关系为：

图9 半锥角误差

Δα圆锥姿态解算<Δα欧拉角姿态解算<Δα双步(圆锥姿态)<Δα双步(欧拉角)

4 结论

考虑了锥形运动存在的不同形式，提出了一种圆锥姿态解算方法，同时为提高该方法的适应性，给出了基于旋转矢量的解算过程，通过与传统姿态解算方法对比发现：

1)相比传统方法，圆锥姿态解算方法的精度高于欧拉角姿态解算方法。

2)基于双步姿态解算的圆锥姿态解算精度高于基于双步姿态解算的欧拉角姿态解算，且常规优化的旋转矢量方法效果并不明显。

文中提出的圆锥姿态解算方法更适合旋转载体的双轴锥形运动条件，能够为旋转载体的复杂角运动解耦和姿态诱导误差抑制的研究工作提供理论参考。未来工作将进一步研究双步姿态解算方法引起姿态出现发散的振荡误差的机理，以及相应的误差抑制方法。