百里杜鹃林区马缨杜鹃凋落物花叶混合比例对分解的影响*

田 奥 王加国 韩振诚 吴佳伟 李苇洁

(1.贵州省山地资源研究所 贵阳 550001; 2.贵州大学林学院 贵阳 550025)

森林凋落物分解是物质循环和能量流动的重要环节(刘洋等， 2006； 王春阳等， 2010； 张晓鹏等， 2011)，它通过改变土壤的C、N、P等元素含量而改善土壤肥力(Melilloetal., 1982； Bergetal., 2003)及林地生产力(Knoeppetal., 1997)。自然凋落物多是不同物种或不同器官的混合物，因各组分的质地、结构及比例等差异以及其交互作用而使分解过程复杂，难以采用各组分的分解速率直接推算整体分解速率(郭晋平等， 2009； 张林海等， 2012)。混合凋落物的分解速率通常高于(协同效应)或低于(拮抗效应)各单一组分分解速率的质量加权平均值，表现为凋落物混合的非加和效应(熊勇等， 2012)，其大小可能随分解阶段而变(Marcoetal., 2011； 肖玲艳， 2015)，对这一问题的理解有利于准确量化凋落物分解动态。

目前，对凋落物分解的非加和效应研究多聚焦于不同物种组成或不同分解阶段凋落物的质量损失、营养物质转移和微生物丰富度等方面，综合考虑分解时间、物种或器官混合比例等影响的研究还鲜有报道。凋落物分解模型可模拟分解动态及量化非加和效应。很多学者建立了考虑环境影响的凋落物分解过程模型(Zhangetal,. 2010; Wallmanetal., 2004)，可很好地解释凋落物分解机制，然而因模型运行时的环境因子繁杂，不适于在连续时间尺度上应用。相比之下，描述凋落物残留率随分解时间变化的Olson模型结构简单，在各类生态系统得到广泛应用(Olson, 1963; Nunesetal., 2015)。

贵州毕节百里杜鹃(Rhododendronspp.)林的主要经济功能是提供旅游资源，可给贫困地区带来较高经济收入(贾真真等, 2012)。因该林区地处土层浅薄、营养贫乏的喀斯特地区，枯落物层还发挥着保护土壤、固碳、涵养水源、净化水质等多种重要功能，在维持枯落物层合理厚度及分解速率的同时，维持着杜鹃群落的稳定。马缨杜鹃(Rhododendrondelavayi)是当地杜鹃群落的建群种和优势种(潘端云等， 2019)，其叶厚、革质，叶背长有厚厚的绒毛，因而难以分解； 花序顶生，且由10～20朵小花构成圆球状，花凋落量大，花期末的林地凋落花朵约占年花叶凋落物总量的19.3%，对枯落物层的物质组成、分解速率和生态水文功能等有重要影响。此外，杜鹃花有较高药用价值，在花期收集新鲜的花凋落物，可为当地带来新的经济增长点。然而如何确定花凋落物的合理采集强度，且不影响凋落物分解及枯落物层的结构与功能，进而维持生态系统稳定，是亟待解决的问题。鉴于此，本研究以马缨杜鹃为例，设置不同花叶比例的混合凋落物野外分解试验，量化凋落物残留率随分解时间及花叶比例的变化，评价凋落物分解的非加和效应，以期为确定花凋落物的合理收集强度提供理论依据。

1 研究区概况

百里杜鹃林区位于贵州省西北部毕节市的大方县与黔西县交界处(105°45′30″—106°04′45″E，27°08′30″—27°20′00″N)，属北亚热带季风湿润气候，年均降水量1 181 mm，年均气温11 ℃，气候总体温和，但极端气温可高达30 ℃或低至-10 ℃，冬季较湿润，春季较干燥，年均空气相对湿度为80%。当地土壤为煤系底层发育而来的酸性土壤(骆强等， 2010； 吴倩楠等， 2010)。百里杜鹃林区是地球同纬度范围内迄今发现的中低海拔区面积最大的天然杜鹃林(李苇洁等， 2008)，面积125.8 km2，分布着马缨杜鹃、露珠杜鹃(R.irroratum)和迷人杜鹃(R.agastum)等杜鹃属植物35种(含亚种、变种)，分属6个亚属、4个组及9个亚组(陈翔等， 2010)，3—4月为花期(40～50天)。作为当地优势种和建群种的马缨杜鹃，面积约25.16 km2，占百里杜鹃林区总面积的20%。

研究期间(2016年4月1日—2017年3月31日)内，各月平均气温13.0 ℃，总降水量1 092.3 mm，最大月降水量为6月份的310.5 mm，最高月均气温为7月份的22.3 ℃(图1)。

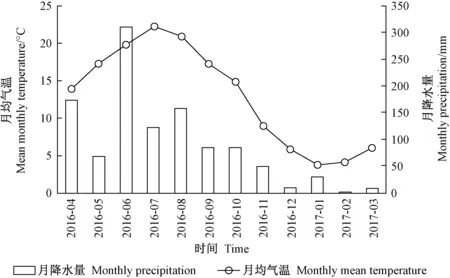
图1 研究期间百里杜鹃林区的月均气温及月降水量

2 研究方法

2.1 试验设计

2016年3月在林区布设凋落物收集器，选取3个马缨杜鹃典型纯林地段，各设5 m×5 m的固定样地12个，每样地沿对角线均匀放置1 m×1 m×0.1 m的凋落物收集器4个，于2016年3—4月每2天收集1次凋落物，将花和叶区分后分别称鲜质量，带回室内60 ℃烘干后称干质量。

将烘干的花和叶按不同质量比例混合，总质量20 g，装入尼龙分解袋(网眼1 mm，规格25 cm×25 cm)。共设7个处理： 花100%+叶0(10F∶0 L)、花50%+叶50%(5F∶5 L)、花40%+叶60%(4F∶6 L)、花30%+叶70%(3F∶7 L)、花20%+叶80%(2F∶8 L)、花10%+叶90%(1F∶9 L)和花0+叶100%(0F∶10 L)。每个处理60袋，合计420个分解袋。均于4月1日(后面记为分解第1天)置于固定样地的林内地面，尽量和凋落物自然状态一致。分别在野外布设后的第61、122、183、244、306和365天，从各处理中随机抽取5～6个分解袋，带回室内自然风干后继续60 ℃烘干至恒质量，计算凋落物分解质量数据。

2.2 凋落物化学组成测定及初始含量

将尚未分解的凋落物烘干样品用粉碎机粉碎后，过孔径2 mm的筛，然后装袋，用于测定化学成分的初始含量。其中C含量用重铬酸钾-浓硫酸氧化法测定(鲁如坤， 1999)； N含量用半微量凯氏法测定(鲁如坤， 1999)； 木质素、纤维素及葡萄糖等物质含量用范氏(Van Soest)洗涤纤维法测定(Rowlandetal., 1994)。纯花与纯叶的化学组成初始含量见表1。

表1 纯花、纯叶凋落物的化学组成及初始含量

2.3 花叶混合凋落物残留率模型

2.3.1 Olson指数衰减模型 Olson指数衰减模型于1963年提出，最初用于描述生态系统中能量和物质的衰减过程，后逐渐广泛应用在凋落物分解过程中。具体形式如下：

R=Mt/M0×100%;

(1)

R=exp(-kta);

(2)

D=ΔM/Δt。

(3)

式中:R为凋落物残留率(%);D为凋落物分解速率(g·d-1);M0及Mt分别表示凋落物初始干质量及分解t天后残留干质量(g)； ΔM为Δt天内凋落物残留物的质量损失量(g)；a和k为待拟合参数。

2.3.2 混合凋落物的非加和效应 花叶凋落物混合的非加和效应可由混合凋落物的理论残留率(T)与实测残留率(O)的差值计算获得：

T=rf×R100+(1-rf)×R0；

(4)

NA=T-O。

(5)

式中:rf为分解开始前花凋落物占总凋落物的质量比例(%)，相应的叶凋落物比例为1-rf；R100及R0分别为纯花及纯叶凋落物残留率； NA为混合凋落物的非加和效应，正值表示对分解有促进作用，反之为抑制作用。

2.3.3 基于Olson改进模型的花叶混合凋落物分解残留率模型 为基于分解时间和花比例来预测不同花叶比例和分解时间的凋落物残留率，首先基于非加和效应NA响应花比例(rf)及分解时间(t)的观测数据，确定NA对这2个单因素的响应函数f(rf)及f(t)并进行耦合——NA=f(rf)×f(t)，则凋落物残留率模型为：

R=f(rf)×f(t)+R100×rf+R0×(1-rf)。

(6)

基于实测数据，拟合凋落物残留率模型的参数，并通过决定系数(R2)和均方根误差(RMSE)的比较，评定拟合效果。R2越高，拟合精度越高； RMSE越小，误差越小，则模型拟合效果越好。

2.4 数据处理

通过SPSS软件进行单因素方差分析(One-way ANOVA)，并基于邓肯法检验结果的显著性。图表绘制用Origin8.0软件完成。模型参数率定用1stOpt1.5完成。

3 结果与分析

3.1 花叶比例及分解时间对凋落物残留率和分解速率的影响

各花叶比例凋落物的累积残留率表现为随分解时间增加而逐渐降低，随花凋落物比例增加累积分解率逐渐增大(图2)。纯花(10F:0 L)、5F:5 L、4F:6 L、3F:7 L、2F:8 L、1F:9 L和纯叶(0F:10 L)处理分解1年后的残留率分别为55.2%、55.5%、56.2%、56.8%、60.2%、58.7%和63.1%。除5F:5 L处理的凋落物累积残留率在183天以前略低于纯花凋落物残留率以外，其余各混合处理以及在各时间的残留率均介于纯花和纯叶处理之间。

图2 不同花叶比例的混合凋落物的分解残留率及分解速率随分解时间的变化

在凋落物分解过程中，不同阶段的分解速率差异很大(图2)，各花叶比例的凋落物分解速率在第0～61天最高，平均为0.054 g·d-1，其中5F:5 L处理最大(0.07 g·d-1)，纯叶凋落物处理最低(0.031 g·d-1)。在以后各次测定中，各处理的阶段分解速率均大幅降低且差异大幅减小。在第62～122、123～183天，各处理的阶段分解速率均值(变化范围)分别为0.017(0.014～0.021)、0.016(0.014～0.019)g·d-1，整体均值为0.017 g·d-1。在第184～244、245～306天，即当年10月初到翌年2月初，各处理的阶段分解速率均值(变化范围)又有提高，分别为0.026(0.023～0.029)、0.022(0.021～0.027)g·d-1。在第307～365天，即第2年花开前的最后1个月，阶段分解速率最低，其均值(变化范围)仅为0.005(0.002～0.01)g·d-1。

3.2 凋落物分解率的非加和效应及其随花叶比例和分解时间的变化

基于凋落物分解实测数据计算的各时段内凋落物分解的非加和效应的时间变化见图3，花叶凋落物混合均表现为提高分解率的协同效应。因协同效应而增加的分解率表现为随分解时间增加先明显增加后缓慢增加或轻微降低的变化趋势。依据图3中协同效应拟合关系的预测曲线，处理1F:9 L及2F:8 L的协同效应在分解365天后最大，分别为7.8%及4.7%； 处理3F:7 L、4F:6 L及5F:5 L的协同效应分别在分解333、310、270天后最大，分别为6.9%、6.8%及6.6%。

由图4可知： 各花叶比例凋落物分解的协同效应在183天以内均表现为随花比例增加而一直增大； 但在183天以后表现为先升高后逐渐平稳(或轻微降低)。在第1次(分解61天后)、第2次(122天)和第3次(183天)取样时，协同效应均在花比例为50%时最大，分别是6.9%、4.7%和3.2%。在分解到244、306及365天时，协同效应在花比例为37%、35.6%及34%时最大，分别为6.4%、9.4%及6.5%。

3.3 考虑非加和效应的凋落物残留率模型率定及应用

基于3.2节的分析可知，非加和效应(协同效应)对花比例及分解时间的单因素响应关系均可表示为一元二次方程，耦合这2个因素作用的非加和效应模型可表示为：

(7)

式中a1，a2，b1，b2为待拟合参数，将式(7)带入式(6)，即可建立同时考虑非加和效应、花比例、分解时间影响的花叶凋落物分解的残留率模型。利用实测数据率定了模型参数(式8)，其决定系数高达0.987，均方根误差为0.017。

(-0.000 68×t2+0.283×t)+

exp(-0.037×t0.507)×

rf+exp(-0.001 7×t0.957)×(1-rf)。

(8)

R2=0.987

图3 不同花叶比例凋落物分解的非加和效应提高的分解率随分解时间的变化

图4 不同花叶比例凋落物分解的非加和效应提高的分解率在不同分解时间随花比例的变化

利用模型(8)模拟分析了在4个分解时间的残留率对花比例的响应(图5)。凋落物残留率整体上随花比例增大而先逐渐降低，在达到最低值后转而平稳(或小幅升高)，但在不同分解时间中又有所差异。在凋落物分解91天后，残留率随花比例增加几乎一直降低，纯花处理的累积残留率为76.8%(即分解率为24.2%)； 在分解183、274及365天后，残留率在花比例为80%、70%和80%时达到平稳状态(或最低)，分别为67.2%、60.6%和52.0%，对应的累积分解率最大值分别为32.8%、39.4%和48.0%。

基于对接近自然情况的花比例20%及更低的几个花比例的模拟结果(图5)表明，当花比例分别为20%、15%、10%、5%和0%时，分解1年后的残留率分别为59.6%、61.0%、62.4%、64.0%和66.0%，对应累积分解率分别为40.4%、39.0%、37.6%、36.0%和34.0%。

图5 混合凋落物残留率随花比例和分解时间变化的模拟

3.4 自然条件下凋落物残留率的多重比较

考虑到自然条件下花凋落物占花叶凋落物总质量的19.3%，因此仅将花比例20%以内的凋落物分解处理的残留率进行多重比较(图6)。对2F:8 L及1F:9 L 2个处理，仅在分解61天后的残留率存在显著差异(P<0.05)，在其余时间均无显著差异，且二者的残留率均显著低于纯叶处理(0F:10 L)的残留率。这说明，将待分解凋落物的花比例控制在10%时，不会明显降低分解率，且在第306和365天的实测分解率还比20%花比例的略有升高。因此，结合3.1节的分析，认为合理控制花凋落物采集强度，使剩余凋落物的花比例维持在10%以上，可保持凋落物分解接近自然，以维持林地枯落物层结构与功能的稳定。

图6 不同花叶比例的混合凋落物野外分解不同时间后的残留率差异的多重比较

4 讨论

4.1 花叶混合对凋落物分解的非加和效应

凋落物组分混合后对分解速率的非加和效应在许多树种及器官的混合凋落物分解中普遍存在。例如在将质地较硬但易于分解的冬青栎(Quercusilex)叶片与革质并覆被蜡质物从而较难分解的蔷薇Cistusincanus及C.salvifolius叶片混合后的分解试验中(Marcoetal., 2011)，累积分解率随栎叶比例增大而提高，非加和效应表现为添加栎叶的协同效应或添加蔷薇叶的拮抗效应。这与本野外分解研究的结果相似，即提高马缨杜鹃花凋落物比例后，其非加和效应表现为协同效应，促进凋落物分解。

对不同树种(阔叶或针叶)叶片混合凋落物分解的文献的综合分析表明，凋落物混合的促进分解作用很常见，在108组混合凋落物中有77组为促进效应，平均使凋落物分解率提高20%左右(1%～65%)(Gartneretal., 2004)。凋落物分解主要受N含量、C/N及木质素/N的比值等多种因素影响(Gessneretal., 2010)，因而难以明确凋落物分解中非加和效应的形成原因。对不同混合比例的赤松(Pinusdensiflora)与枹栎(Q.serrata)叶片凋落物分解的非加和效应研究(Salamancaetal., 1998)，其结果与本研究极为相似，即协同效应随易分解成分(栎叶片)比例的增加而增大。在分解1年后，随着栎叶质量比例从25%增至75%，提高混合凋落物分解率的协同效应从1.1%提高到2.8%，这一数值明显低于本研究中的协同效应(4.03%～6.1%)，其差异可能是2个试验中凋落物初始N含量C/N和木质素/N比值的差异导致的，尤其是C/N比值的差异。

此外，本研究发现，马缨杜鹃花叶混合的阶段协同效应随分解时间而变，表现为先明显增加后缓慢增加或轻微降低。Marco等(2011)研究表明在分解过程中会出现协同效应和拮抗效应：栎叶中混入蔷薇叶后，前90天的凋落物分解表现为拮抗效应，90～400天内则逐渐变为协同效应。

不同来源的凋落物分解存在着物理、化学和生物过程的差异，不同的分解者(细菌、真菌等微生物以及蚯蚓等土壤生物)有着不同的食物和环境条件要求，这是不同凋落物组分混合后产生分解速率非加和效应的主要原因。例如，在将不同质地和结构的凋落物彼此混合后，凋落物的总表面积及彼此之间的作用空间会发生变化，从而改变分解的作用环境，进而影响分解者的丰富度及多样性，使原单一凋落物的营养物质及分解者因混合实现再分配并最终影响分解过程(Hansenetal., 1998;Gessneretal., 2010)。

4.2 分解时间对凋落物分解速率的影响

本研究中各花叶比例凋落物的分解残留率均随时间增加逐渐降低，分解1年的残留率变化在55%～63%，与贵州茂兰喀斯特森林凋落物的分解残留率基本相似(龙健等， 2019)。大量研究表明，凋落物分解受诸多因素影响，包括凋落物本身特性、环境因子、分解时间等(Liskietal., 2003;Wallmanetal., 2004)。凋落物分解在初期较快和后期较慢，是因易分解物质(糖、淀粉等)含量在分解初期较高，之后迅速降低， 而木质素等难分解物质含量却不断增加(杨万勤等， 2007)。在后期凋落物缓慢分解阶段，分解速率更多受环境因子调控，如水分充足时，温度升高可加速凋落物破碎化及淋溶过程，从而促进分解(马志良等, 2020)。在本研究中，尽管第62～183天内(6—9月)水热条件较好，但阶段凋落物分解速率却迅速降低(图2)，这可能一方面是因易分解物质含量已大幅降低，另一方面可能是6—9月的大量酸性降雨(李贵琼等， 2016)改变了分解者生存环境，导致酶活性逐渐降低，土壤微生物和动物数量减少(季晓燕等， 2013)。在分解后的第184～306天(10月至翌年2月)，虽然月均气温和月降水量均明显下降，但阶段分解速率却有所上升，这一方面可能是因为降水量减少缓解了酸雨抑制作用，另一方面可能因秋末及冬季降水淋溶物的加入改善了凋落物的分解环境，导致网袋内凋落物的分解速率得到提高。在研究期间的最后一个时段(307～365天)，其阶段分解速率最低，这应主要是因凋落物中易分解物质含量不断降低和难分解物质含量不断提高。

4.3 花叶混合比例对凋落物分解的影响

在本研究中，当混合凋落物中的花比例为0～50%时，凋落物分解残留率随花比例增大而降低，即花越多分解越快，这可能首先与花、叶凋落物的N初始含量有关。许多研究表明，N含量较高的凋落物(C/N低)分解更快(Wardleetal., 1997)。这是因凋落物分解一般易受N含量不足的限制，因而N含量可影响分解者的生理活动，较高N含量会促进分解(赵琼等， 2010)。马缨杜鹃的纯花凋落物的N初始含量为1.3%，远高于叶凋落物的N初始含量0.6%(表1)，因此提高花比例会加快凋落物分解。

基于混合凋落物的分解残留率模型预测，可知分解最快的花叶比例介于7F:3 L及8F:2 L之间，即理论上说将花凋落物的质量比例维持在70%～80%时最能促进凋落物分解。然而自然条件下的花凋落量仅占花叶总凋落量的19.3%，在高于此花比例的范围内人为增加花凋落物并不具备生产实操性，而是需在低于自然花凋落物比例的范围内寻找合理利用强度。基于不同花叶比例处理的凋落物分解过程实测值及其差异的多重比较结果可知，花比例20%和10%时的2个处理在分解1年后的残留率无显著差异，且两者均显著高于纯叶凋落物的残留率。由此建议将花凋落物的合理收集利用强度控制在一半以内，这样不会明显影响凋落物分解及林地枯落物层的数量和结构。

4.4 不足与对未来研究建议

本研究围绕自然花凋落物比例19.3%，仅设置了花比例为10%及20% 2个梯度及纯叶凋落物处理，仅凭2个梯度还难以确定最佳的花凋落物收集强度。建议未来继续增加花比例梯度，尤其是在0～20%的花比例范围内，以确定最佳的花凋落物利用强度。

5 结论

贵州百里杜鹃林区的马缨杜鹃不同花叶混合比例的凋落物1年野外分解试验表明： 花凋落物混入叶凋落物后有促进分解的非加和效应，基于非加和效应建立了凋落物分解残留率随分解时间和花比例变化的模型，精度高达0.987，该模型可模拟分析不同花叶比例的凋落物分解残留率的时间变化过程。通过模拟可知，当将花比例从靠近花凋落物自然比例的20%降至15%、10%、5%、0时，分解1年后的残留率从60.0%分别升至61.3%、62.8%、64.4%和66.1%； 基于野外分解1年后的残留率实测值的多重比较，表明花比例为10%及20%的2个凋落物处理差异不显著，且均显著低于纯叶凋落物的残留率。鉴于花凋落物的自然比例接近20%，建议花凋落物收集利用强度不要超过一半，以尽量不影响凋落物分解，维持林地枯落物层的结构与功能稳定。