碟盘刀具振动切削煤岩的理论力学模型与载荷特性

刘春生，李德根，袁 昊

(1.黑龙江科技大学,黑龙江 哈尔滨 150022; 2.黑龙江科技大学 机械工程学院，黑龙江 哈尔滨 150022)

机械刀具破碎硬煤岩是实现煤矿安全绿色开采的重要途径，研制高效破碎硬煤岩的刀具是基础，而刀具破碎煤岩机理是设计高性能刀具的基础。EVANS[1]认为煤岩的断裂是由于拉应力造成的。ROXBOROUTH等[2-3]考虑截齿与岩石之间的摩擦，改进了EVANS 的截割力模型。BILGIN等[4]在岩石直线截割试验的基础上，利用试验得出的数据和岩石强度、截割厚度等参数建立了其理论计算模型。BAO等[5]考虑截齿侵入岩石过程中的能量耗散，基于断裂力学建立了力学模型。赵光明等[6]采用理论分析和数值模拟研究了巷道围岩承载结构特性。牛东民[7]以断裂力学的角度建立了刀具切削煤岩的破碎机理。梁运培等[8]试验研究了不同截割厚度、截线距下，镐型截齿破岩力学参数与截割厚度和截线距之间的关系。除刀型和镐型截齿机械破碎煤岩外，还有冲击破岩、冲击-切削破碎等方法在采煤和隧道掘进有广泛应用[9-12]。李润成等[13]通过试验证明有振动比无振动可以有效减少截割阻力。MURO[14]研究振动切削凝灰岩时，指出振动时与无振动时的水平切削阻力之比随振动频率增加呈双曲线下降、正弦波振动时的切削效率比三角波振动时的高。谢世勇等[15]指出随着冲击能的增大，岩石破碎深度及破碎体积均增大，破岩比能不是随冲击能的增加而减小，存在一个最佳破岩冲击能。李思琪等[16]基于有限元研究了复合荷载作用下冲击岩石的压痕效应。刘春生等[17-20]基于非对称截槽建立了镐型截齿破碎煤岩的力学模型,同时还建立了边缘牙齿刀盘单刀齿破碎煤岩的理论计算模型，得出在轴向振动与径向切削复合作用下比单作用具有更佳破岩效果。纪照生[21]基于岩石重力针对高频振动冲击技术进行了破碎机理的研究。

结合上述学者所提出的理论、数值模拟和试验等研究成果，笔者通过分析振动与切削复合作用的破碎方式和截割碟盘刀具的力学特点，通过研究其破碎煤岩的载荷特性，建立碟盘刀具破碎煤岩载荷理论计算的模型，通过与数值模拟和试验载荷峰值均值的对比分析,验证理论模型,为振动与切削复合作用破碎煤岩截割机构的研制提供载荷设计依据。

1 煤岩崩落面积与当量崩落角

1.1 煤岩崩裂面积

由图1可知：

(1)

式中，lx=lmcosφ。

由式(1)可得

(2)

图1 碟盘刀具崩落面积和当量崩落角Fig.1 Disc cutter caving area and equivalent caving angle

(3)

(4)

整理可得

(5)

1.2 煤岩当量崩落角

碟盘刀具楔面近似圆台，破碎煤岩时载荷由碟盘刀具中间向两侧逐渐递减，破碎煤岩的崩落角在刀具楔面与煤岩接触处也是逐渐变化的。因此，煤岩的当量崩落角及其位置角，是碟盘刀具切削煤岩的楔面集中作用力的前提。在0～π/2内等效，由图1可得煤岩当量崩落角ψd。

(6)

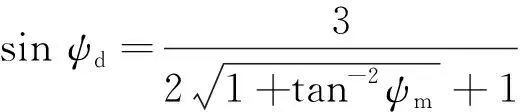
(7)

根据文献[17]中切削厚度与崩落角的关系可知ψm对应不同的hm,则由式(7)可求得不同切削厚度下的当量崩落角ψd。

2 楔面破碎煤岩的作用力模型

2.1 集中力的作用点和位置角

碟盘刀具由刀刃和楔面两部分组成，在切削煤岩时，刀刃有助于刀具楔入煤岩，楔面部分则有助于煤岩的大块崩落。由碟盘刀具的结构特点计算出等效集中力的作用位置角度，碟盘刀具破碎煤岩楔面作用力学模型如图2所示，图中，h1d为刀具任意位置与煤岩的接触厚度，mm。

图2 碟盘刀具破岩等效集中力学模型Fig.2 Equivalent concentrated mechanical model of disk cutter breaking rock

由图2可知，

(8)

式中，N1，N2为等效集中力分力，kN;dNT为单元等效集中力，dNT=dNMcosφ=N0cosφdφ，kN,NM为单元位置角所对应的楔面载荷，kN;N0为破碎煤岩时的楔面载荷[16]:

(9)

式中，f1为刀齿与煤岩之间的摩擦因数。

由式(8)可计算在0～π/2内合力及作用点，可得

(10)

(11)

则可得等效集中力和位置角分别为

(12)

tanψd=N2/N1=2/π,ψd=32.5°

(13)

2.2 楔面破碎煤岩的准则

碟盘刀具在振动与径向切削复合运动破碎煤岩时，楔面逐渐进入煤岩体内，当达到一定楔入距离后，楔面逐渐起主导作用，完成对煤岩的大块崩落。碟盘刀具在轴向以正弦规律运动，在不同工况下煤岩破坏准则也不同，按煤岩单向受力状态即单轴受力，在计算碟盘刀具破碎煤岩时按照抗拉或抗剪强度条件分别建立碟盘刀具破碎煤岩的力学模型，按照达到最小能量法则来确定破碎煤岩准则。

图3为碟盘刀具在轴向向上振动与径向切削复合作用时A—A′剖面楔面与煤岩的力学模型，图中，vz为轴向振动速度，m/s;vj为径向切削速度，m/;ΔL1为刀具运动合成速度与水平方向的夹角大于刀具对煤岩的正压力与水平运动方向的夹角时，O点到楔面作用力的垂直距离相对于O点到刀齿齿尖作用力的垂直距离的增量，mm;L1为刀具运动合成速度与水平方向的夹角大于刀具对煤岩的正压力与水平运动方向的夹角时，O点到刀齿齿尖作用力的垂直距离，mm;NT1为刀具与煤岩的摩擦力,kN;NT2为楔面对煤岩的作用力，kN;T2为刀具向上振动时刀头对煤岩的作用力,kN;T3为刀具径向切削时刀头对煤岩的作用力,kN;δ为刀具向上振动时刀头对煤岩的作用力与水平方向的夹角，(°);β为刀具径向切削时刀头对煤岩的作用力与水平方向的夹角，(°);ΔL2为刀具与煤岩未有相对运动时，O点到楔面作用力的垂直距离相对与O点到刀齿齿尖作用力的垂直距离的增量，mm;L2为刀具与煤岩未有相对运动时，O点到刀齿齿尖作用力的垂直距离，mm;αzj为刀具运动合成速度与水平方向的夹角;φ为刀具对煤岩的正压力与水平运动方向的夹角，其中φ=π/2-α;ψd为刀具破碎煤岩时的当量崩落角;ξ为刀具与煤岩之间的摩擦角。

2.2.1αzj>φ结果分析

图3 A—A′碟盘刀具破碎煤岩等效位置Fig.3 A—A′ Disk cutter broken coal rock equivalent position

由图3并且根据假设条件可计算对y轴的静矩为

(14)

同理，可求得对x轴的静矩为

(15)

由式(14),(15)可得出形心位置为

(16)

式中,lm=hm/tanψm，hm为14～30 mm，参见文献[18]切削厚度与崩落角之间的关系，可知每一个切削厚度对应相应的ψm，分别为30.8°,34.0°,36.7°,39.0°和41.0°，由式(16)可知，当lm/R的值比较小时可得到φc≈arctan(2/π)，因此由式(16)可得出在给定的参数计算出不同切削厚度下图形水平投影的形心位置角度φc近似为32.5°，与式(13)求得的位置角一致。

由护士长作为组长,科室护理人员作为组员,组成风险管理小组,旨在加强医护人员的风险意识,并展开技能培训工作,提升人员的专业素质。作为科室护士长应该根据科室的制度流程,安排护理人员对患者病情进行全面掌握,尤其是对于一些病情程度严重的患者,应该坚决杜绝安全隐患,定期抽检护理人员的工作执行情况,加强监控。

根据图3所示的力学模型，在计算刀具破碎煤岩载荷(与对煤岩的作用力方向相反)时，建立碟盘刀具与煤岩作用的力学平衡方程:

(17)

NTτtsin(α+ψd-ξ)+T3cosβcosψd+

T2cos(ψd-d)=τtS′+f1T3cosbcosψd+

f1T2sin(ψd-d)-f1NTτtcos(a+ψd-x)

(18)

由式(17)，(18)可得

(19)

(20)

煤岩之间的抗拉强度、抗剪强度与抗压强度存在一定的关系，岩石的抗剪强度约为其抗压强度的0.09～0.20，岩石的抗拉强为抗压强度的0.07～0.10，抗拉与抗剪强度为:σl=kτ，其中k为比例系数，k∈(0.50～0.73)。

2.2.2αzj=φ结果分析

当αzj=φ时，由图3(b)的力学模型可知，刀具与煤岩没有相对运动，因此刀具给煤岩的正压力即为刀具作用于煤岩的合力。同理，按照抗拉和抗剪强度准则及刀具与煤岩的力学平衡方程，此时煤岩所受拉力为式(19)中ξ取0，所受剪力为式(20)中ξ取0。

2.2.3αzj<φ结果分析

当αzj<φ时，由图3(c)力学模型可知，刀具对煤岩的摩擦力沿楔面向下。煤岩所受拉力为式(19)中ξ取-ξ，所受剪力为式(20)中ξ取-ξ。

由式(19)，(20)进行计算对比由最小能量原则可得，当楔面角度为35°、切削厚度为18～26 mm，NTσlNTτt说明达到抗剪强度为破坏准则。因此根据以上的计算及最小能量原则可得Nm=min(NTσl，NTτt)，Nm为根据最小能量原则得出的楔面作用力。

3 破碎煤岩载荷的理论模型

研究碟盘刀具破碎煤岩的载荷特性及破碎煤岩的理论模型显得尤为重要，煤岩破碎理论是对煤岩破碎机构和采掘机械装备、受力分析以及截割参数确定的重要依据。

当碟盘刀具轴向振动与径向切削复合破碎煤岩时，根据煤岩破碎准则，分别在αzj>φ,αzj=φ和αzj<φ的3种情况下不同的破碎煤岩准则给出碟盘刀具破碎煤岩的载荷模型。

由式(18)，(19)结果可知，楔面角度为35°～55°,切削厚度在30 mm以内时按所计算达到的破坏强度准则，对刀具楔面的作用力与刀刃的作用力进行矢量叠加算碟盘刀具破碎煤岩径向Fji与轴向载荷Fzi，可得

式中，Nmi为不同刀具作用力与水平方向夹角下所对应的最小能量原则得出的楔面作用力，kN;ωi为刀具作用力与水平方向的夹角，当i=1时为αzj>φ，此时ω1=α-ξ;当i=2时为αzj=φ，此时ω2=α;当i=3时为αzj<φ，此时ω3=α+ξ。

4 载荷理论模型的验证

碟盘刀具破碎煤岩时，碟盘刀具和煤岩的参数见表1，表中，f为振动频率，Hz;A为振动幅值，mm;γ1为径向切削齿尖压力锥体合力与水平面之间夹角的2倍，(°)。

限于篇幅，文中以碟盘楔面角度为50°时，煤岩切削厚度9，14，18和27 mm为例进行数值模拟和试验，验证理论模型的准确性。文中理论模型建立了碟盘刀具远离煤岩工况(碟盘向上振动)的载荷模型，由于理论模型计算载荷值是煤岩大块崩落时载荷，因此对应的数值模拟和试验的载荷峰值均值。

表1 碟盘刀具与煤岩参数Table 1 Disc cutter and coal rock parameters

4.1 数值模拟

为分析碟盘刀具切削煤岩的载荷特性，利用ABAQUS有限元软件在碟盘刀具在轴向振动与径向切削复合作用下破碎煤岩的数值模拟，模拟时在ABAQUS中选用扩展的线性Drucker-Prager塑性本构模型，模拟时碟盘刀具设置为刚体，碟盘刀具和煤岩体采用六面体C3D8R的单元网格类型[19]。碟盘刀具破碎煤岩应力云图，如图4所示。

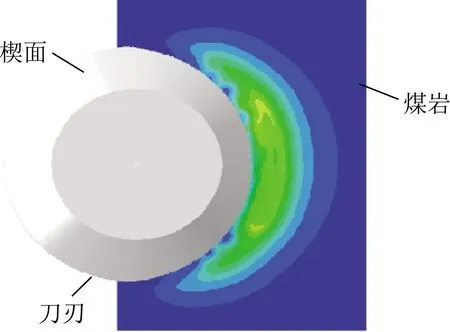
图4 碟盘刀具破碎煤岩应力云图Fig.4 Stress cloud of broken coal rock in disc cutter

由图4可以看出，应力的影响范围呈现出月牙状[19]，由中间向两边递减。

图5为振动切削下，不同切削厚度的碟盘刀具的模拟载荷。

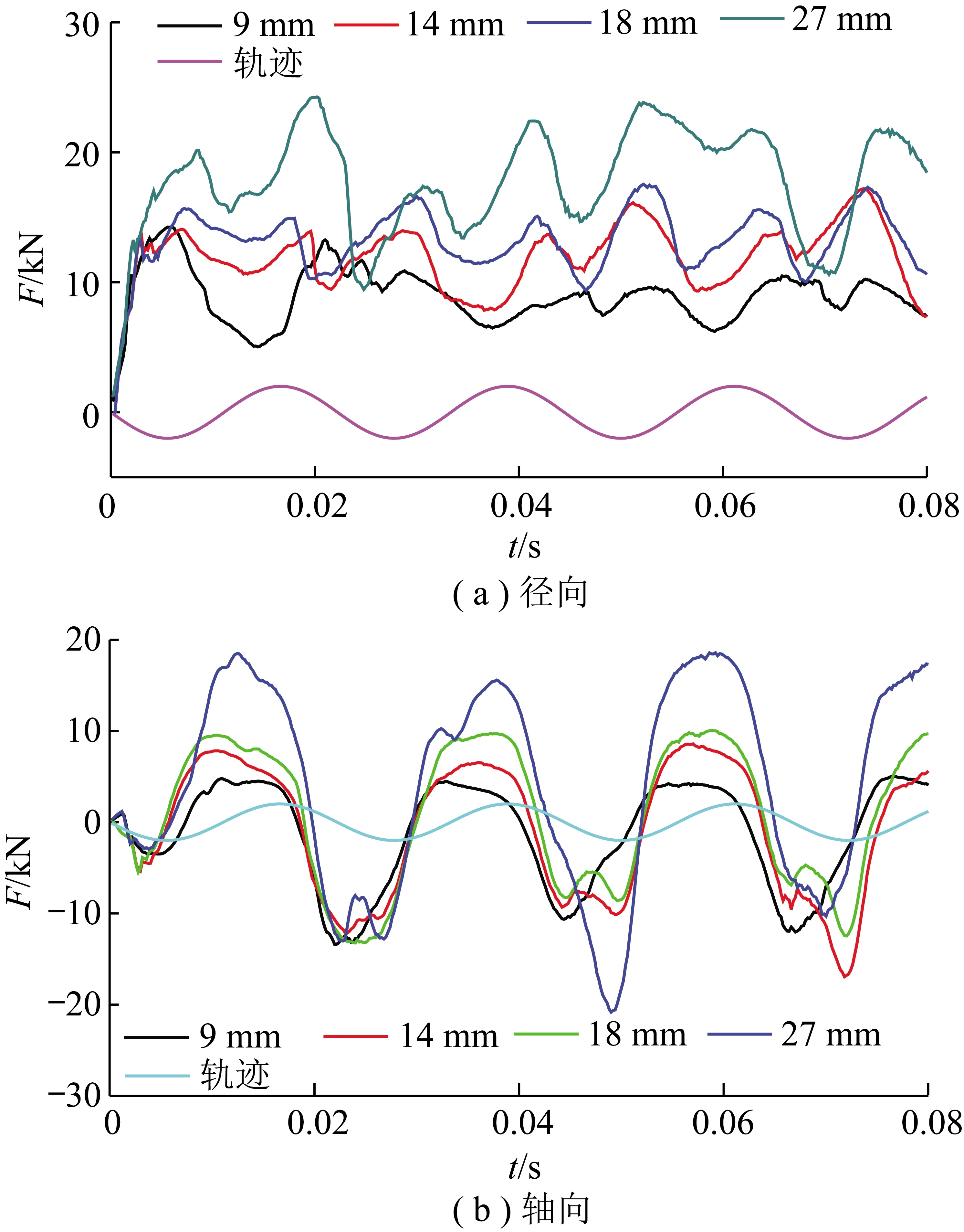
图5 不同切削厚度碟盘刀具的模拟载荷Fig.5 Simulated load of disc cutters of different cutting thicknesses

由图5可知，随着切削厚度的增加，径向载荷逐渐增大，径向载荷和轴向载荷随着振动位移呈周期性变化。

4.2 振动切削煤岩试验

碟盘刀具振动切削煤岩的试验系统如图6所示。该系统包括破岩系统和检测系统，碟盘刀具轴向振动由液压马达驱动振动系统实现碟盘振动破碎煤岩，同时在径向方向液压缸推动截割结构径向切削煤岩。

图6 碟盘刀具振动切削煤岩试验Fig.6 Disk cutter vibration cutting coal rock experiment

由图6可见，振动切削破岩测试系统可测试碟盘刀具径向切削和轴向载荷、液压马达的转速、液压缸的压力以及碟盘刀具的振幅。其中，碟盘刀具振动切削煤岩载荷通过与刀盘连接的弹性轴上的应变片测得，应变片信号经过INV1861D应变调理器处理后输入到INV3060S信号采集分析仪进行采集与处理。碟盘刀具单作用切削的试验载荷如图7所示。碟盘刀具在振动切削时，不同切削厚度的试验径向载荷和轴向载荷分别如图8，9所示。

由图7和图8(a)可知，单作用径向切削试验载荷峰值均值为3.78 kN，振动与切削复合作用下试验载荷峰值均值为27.04 kN，单作用切削载荷约是振动与切削下径向载荷的7倍，说明振动与切削可以明显提升碟盘刀具的破岩能力。由图8可知，随着切削厚度的增加，切削载荷逐渐增大，切削厚度较小时，碟盘刀具的载荷的波动比较小。由图9可见，随着碟盘刀具的轴向往复运动，碟盘刀具向煤壁振动与切削所受的轴向载荷比较大，碟盘刀具远离煤壁时的载荷比较小，“0”线以上为碟盘刀具远离煤壁的振动载荷，“0”线以下为碟盘刀具振动切削煤岩，由于受惯性力等因素影响，轴向载荷较大，呈周期性，文中仅分析“0”线以上部分，对其载荷特性，在其他文章进行详细阐述。

图7 9 mm碟盘刀具切削试验载荷Fig.7 9 mm disc cutter cutting test load

图8 不同切削厚度下碟盘刀具试验径向载荷Fig.8 Test radial load of disc cutters under different cutting thicknesses

图9 不同切削厚度下碟盘刀具的试验轴向载荷Fig.9 Test axial load of disc cutters under different cutting thicknesses

图10 不同切削厚度载荷值的对比Fig.10 Comparison of load spectra of different cutting thicknesses

4.3 载荷的对比分析

根据文中的煤岩破坏准则与给出径向和轴向的载荷计算数学模型，结合式(21)及表1所给的参数计算出碟盘刀具在轴向振动与径向切削复合作用下破碎煤岩的载荷理论值，由于理论分析的是碟盘刀具远离煤壁，该工况下惯性系数K取1。对比分析在数值模拟和试验等效条件下碟盘刀具载荷理论模型计算值与数值模拟载荷峰值均值，理论模型计算值与试验载荷峰值均值的关系，如图10所示。

从图10(a)可以看出，切削厚度为9，14，18和27 mm时碟盘刀具径向载荷的理论模型计算值与模拟载荷峰值的均值误差分别为12.65%，12.85%，3.27%和7.69%，理论模型计算值与数值模拟载荷峰值均值的平均误差为9.12%;切削厚度为9，14，18和27 mm时轴向载荷的理论模型计算值与试验载荷峰值的均值误差分别为4.39%，9.76%，4.56%和0.79%，理论模型计算值与试验载荷峰值均值的平均误差为4.88%。

从图10(b)可以看出，切削厚度为9，14，18和27 mm时轴向载荷的理论模型计算值与模拟载荷峰值的均值误差分别为6.82%，8.27%，7.08%和14.80%，理论模型计算值与数值模拟载荷峰值均值的平均误差为9.25%;切削厚度为9，14，18和27 mm时轴向载荷的理论模型计算值与试验载荷峰值的均值误差分别为22.73%，5.67%，1.89%和5.45%，理论模型计算值与试验载荷峰值均值的平均误差为8.34%。

5 结 论

(1)通过分析碟盘刀具的结构特点与楔面对煤岩的作用力，给出了碟盘楔面在不同工况下煤岩的破坏准则，结合碟盘刀刃对煤岩的作用，采用矢量叠加的方法建立了碟盘刀具在轴向振动与径向切削复合作用下破碎煤岩的径向载荷和轴向载荷理论计算模型。

(2)单作用切削与复合振动切削试验发现，振动与切削煤岩时其径向载荷明显小于单作用径向切削煤岩的载荷，说明研究振动与切削煤岩对提高煤岩切削效率和刀具寿命具有很好的研究价值与应用前景。

(3)碟盘刀具破碎煤岩的径向载荷随切削厚度增加而增大,碟盘刀具在轴向振动与径向切削时不同切削厚度径向载荷理论模型计算值与数值模拟载荷峰值均值的平均误差为9.12%，与试验载荷峰值均值的平均误差为4.88%;不同切削厚度轴向载荷理论模型计算值与数值模拟载荷峰值均值的平均误差为9.25%，与试验载荷峰值均值的平均误差为8.34%，从模拟和试验验证说明所建立的碟盘刀具载荷模型可以满足实际工程需要，下一步继续通过试验研究有齿碟盘刀具的载荷模型。