基于人工神经网络的水厂建设项目造价估算方法

王 祺，周 律,*，马可可，孙 傅，陈宇敏，徐艺星，黄新丽

(1.清华大学环境学院，北京 100084；2.成都环境投资集团有限公司，四川成都 610041)

随着我国城镇化建设要求的不断提高，作为基础设施的自来水厂工程建设项目新建和改造任务十分艰巨。为提高水厂项目的建设投资效益和社会效益，要求对项目全过程的工程造价进行合理和科学的控制与管理[1]。根据国内外大量的工程实践，建设项目前期的工程造价控制对项目的成败起着关键作用。如果能够在项目的前期对工程项目的建设造价和投资进行准确合理的估算，那么项目管理单位对项目造价和投资控制的主动性就越大，项目的风险控制就越有效[2]。

为了实现建设项目造价的快速准确估算，国内外学者提出了多种造价模型或方法，包括第一代的按单位面积的造价估算方法、第二代回归分析方法及第三代基于现代计算机技术的造价估算模型[2-4]。其中，第三代模型中，人工神经网络(artificial neural network，ANN)是对数据信息进行处理以及非线性拟合的一种计算方法。通过人工神经网络构建出的函数，可以揭示所求造价与多个变量间的非线性关系，是一项应用较为广泛的模型[5]。人工神经网络可以视为人造大脑，与人脑的神经系统具有类似结构，可提供解决问题的方法。人工神经网络是通过模拟人脑神经元的信息处理方式，构造大量人造神经元，使其相互联系在一起的网络。目前，国内外已有较多学者将人工神经网络应用建筑工程造价估算领域，且取得了较好的成果[6-16]。人工神经网络模型目前在自来水厂建设项目造价估算的研究和应用缺乏，这与自来水厂建设内容的复杂性有一定的关系。因此，本研究采用我国西南地区自来水厂建设项目的多组工程造价数据，选取人工神经网络中的BP算法和RBF算法，进行自来水厂造价模型的构建与优化，并讨论不同算法下模型的适用性，以期为类似工程项目的造价估算提供帮助。

1 人工神经网络模型的构建

模型的功能是结合各种数学手段或计算软件，确定模型目标值与各类影响因素之间的关系[10]。建立造价模型的第一步，是确定对模型结果有重要影响的相关因素。在人工神经网络模型中，将模型目标值定义为输出值，将影响输出值的相关因素定义为输入变量[11-16]。本研究选用的数据为收集到的以西南地区为主的18份自来水厂建设项目概预算造价数据，对样本数据进行分析后，筛选出18个对工程造价的影响因素作为神经网络的输入变量，如表1所示。输出变量确定为2种，分别是自来水厂工程造价(Y1，万元)及自来水厂吨水造价[Y2，元·(万m3·d)-1]。

在表1中，编号1～3的变量可以描述自来水厂的基本信息。例如，设计处理规模是自来水厂建设的决定性因素；编号4的价格指数这一变量是用于减小不同年份通货膨胀带来的影响，本研究选取国家统计局发布的“建材类工业生产者购进价格指数”，以2018年为基准年，对不同自来水厂的工程造价费用进行调整，尽可能减小通货膨胀带来的影响；编号5～18的变量主要为自来水厂的各类生产性和非生产性构筑物，可以针对具有不同工艺路线的自来水厂自由选择其构筑物种类，选用其建设容积或面积作为变量量化后的数据，即自来水厂选用了6号净水构筑物，则对该变量输入体积值，而没有被选用的7号构筑物则将该变量的体积值输入为0。

表1 神经网络输入变量Tab.1 Input Variables of Neural Network

本研究选用MATLAB软件中的神经网络工具箱进行BP和RBF神经网络模型的构建。首先，将所得的样本数据按3.5∶1的比例随机分为训练组与测试组，即训练组样本共14个，测试组样本4个。

1.1 基于BP算法的模型构建

BP(back propagation)神经网络是一种前馈神经网络，网络由输入层、输出层，以及1个或多个隐藏层组成，核心的BP算法依靠误差逆向传播的方式，以自学习的方式建立并优化模型。BP人工神经网络的每一层均由任意个神经元组成，并通过加权连接的方式相互连接。通常可将模型需要预测的值设定为期望输出值，而与这个预测结果相关的因素定义为输入层的各个神经元，BP人工神经网络则是利用算法的不停迭代，拟合出预测结果与相关因素间的最佳关系[8]。

1.1.1 BP神经网络创建及初始化

调用MATLAB软件中的newff函数，即可创建出1个BP神经网络，同时系统将自行对网络各层的权值和阈值进行初始化。由表1可知，输入变量为18个，输出变量为2个，即神经网络的输入层共18个神经元，输出层共2个神经元。同时，还需对BP神经网络的隐含层层数、各层神经元数量、各层神经网络激活函数进行设置。本研究根据测试组样本结果，不断对网络结构(即隐含层层数、神经元数量、激活函数)进行调整，以获取更高准确度的模型。

1.1.2 BP神经网络训练和仿真

在完成对BP神经网络的创建后，导入选定14组样本数据的输入变量及输出变量，利用样本数据对BP人工神经网络进行学习训练。针对不同的神经网络模型，训练时需对网络参数进行适当的设置或调整。表2是神经网络主要训练参数及取值。

表2 BP神经网络主要训练参数及取值Tab.2 Main Training Parameters and Values of BP Neural Network

对于不同的实际问题，BP神经网络可选择不同的训练函数，本研究选取了常用的Levenberg-Marquardt(trainlm)训练函数。

1.1.3 确定BP神经网络的网络结构

向BP神经网络中导入表2中的14组训练样本数据，通过对样本数据的学习与训练，采用默认神经网络结构的参数，获得初步的BP神经网络模型。

然后，使用测试组中的4个样本数据，对比模型预测值与实际工程造价值的误差，对模型输出值的精确度进行校验。通过不断调整BP神经网络的结构，即隐含层层数、神经元数量、激活函数这3项参数，直至模型输出值与实际工程造价的误差满足预期。

本研究中，神经网络确定了2个输出值：自来水厂工程造价(Y1)和自来水厂吨水造价(Y2)。因此，本研究对2项输出值，分别构建具有不同网络结构的BP神经网络模型，所得神经网络模型的网络结构如表3所示。

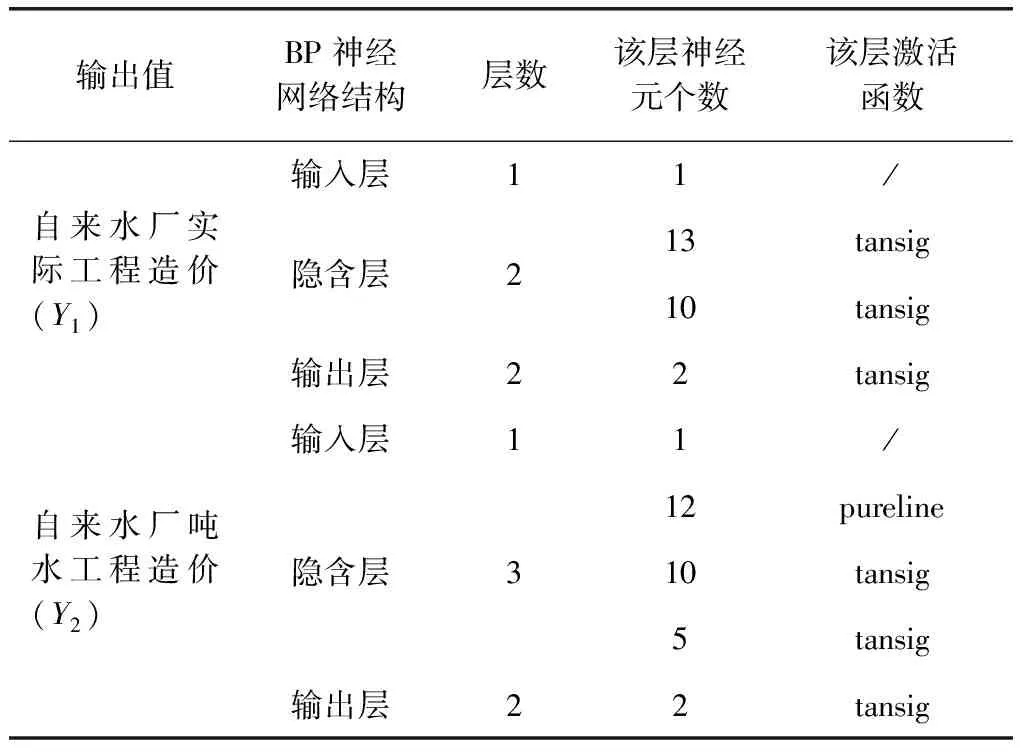
表3 BP神经网络模型结构Tab.3 Structure of BP Neural Network Model

通过MATLAB软件，构建自来水厂工程造价的BP神经网络模型，拟合曲线如图1、图2所示。其中，虚线代表14组样本的实际工程工程造价(Y1)或自来水厂吨水造价(Y2)，实线代表基于BP神经网络模型对14组样本的预测值。由图1、图2可知，2条曲线的重合程度非常高，即代表BP神经模型对样本数据的拟合程度很好。

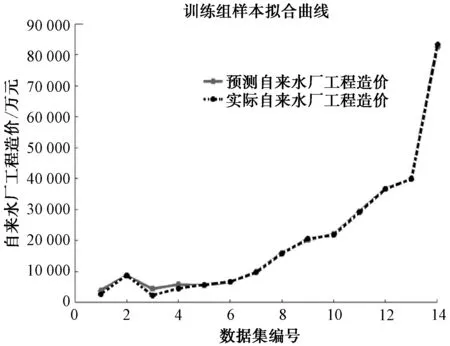
图1 工程造价(Y1)的BP模型拟合情况Fig.1 Fitting Situation of BP Model for Construction Costs (Y1)

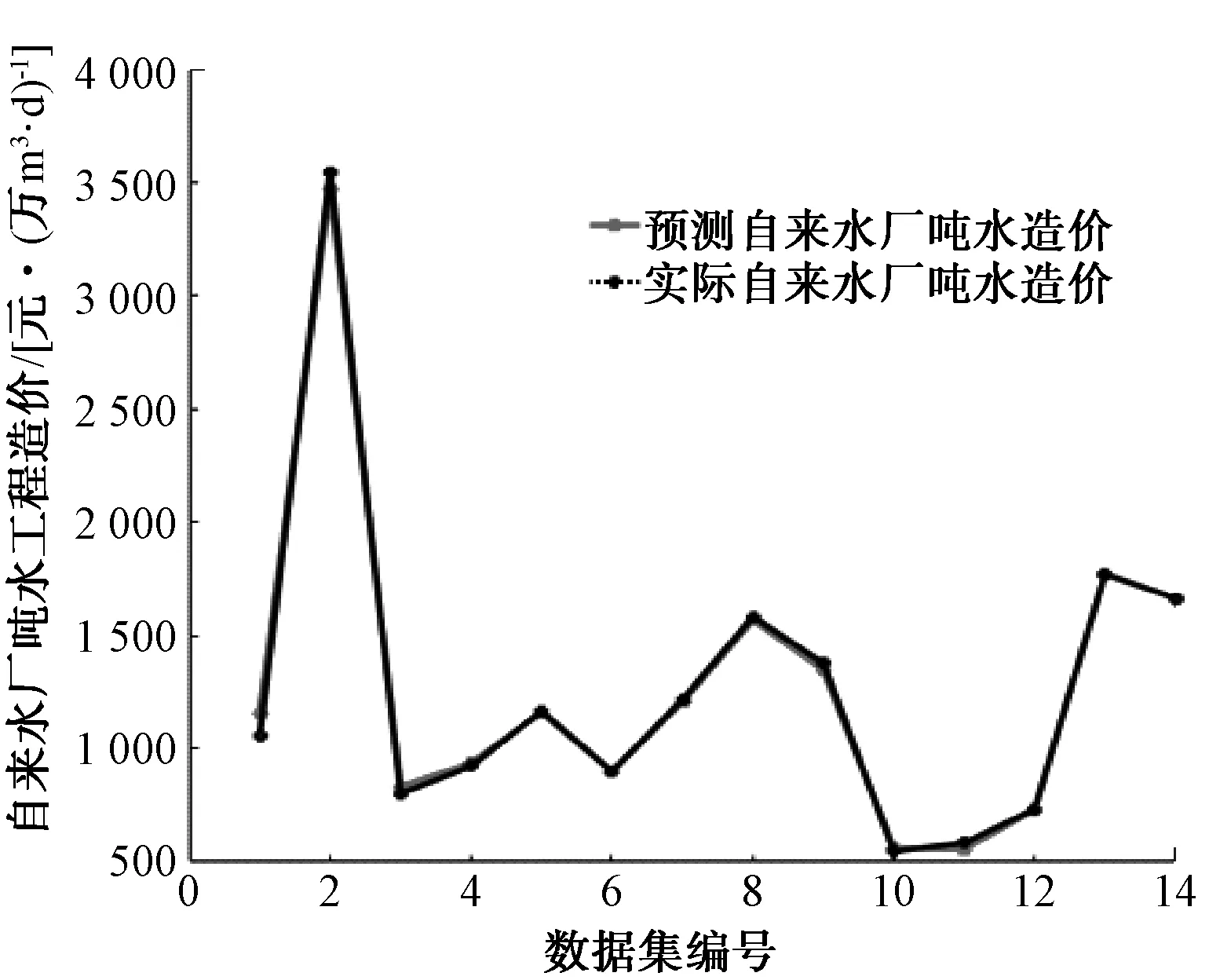
图2 吨水工程造价(Y2)的BP模型拟合情况Fig.2 Fitting Situation of BP Model for Unit Construction Cost (Y2)

1.2 基于RBF算法的模型构建

RBF(radial base function)神经网络是一种局部神经网络，具有结构简单、训练简洁、学习收敛速度快等优点[6]。与BP神经网络一样，能够以任一精确度逼近连续函数。与BP神经网络相似的是，RBF神经网络同样也由3部分组成：第1层是输入层，神经元数量由输入变量的个数决定；第2层是隐含层，网络的激活函数选用的是径向基函数；第3层为输出层，采用线性激活函数。

调用MATLAB软件中的newrb函数，即可创建出1个RBF神经网络。向RBF神经网络中导入14组训练样本数据，网络将自动对样本数据进行反复的学习与训练，自行确定RBF神经网络的结构，无需进行如BP神经网络的参数调整工作，只有1个参数spread需要调整，取默认值1.0。RBF的网络结构如表4所示。

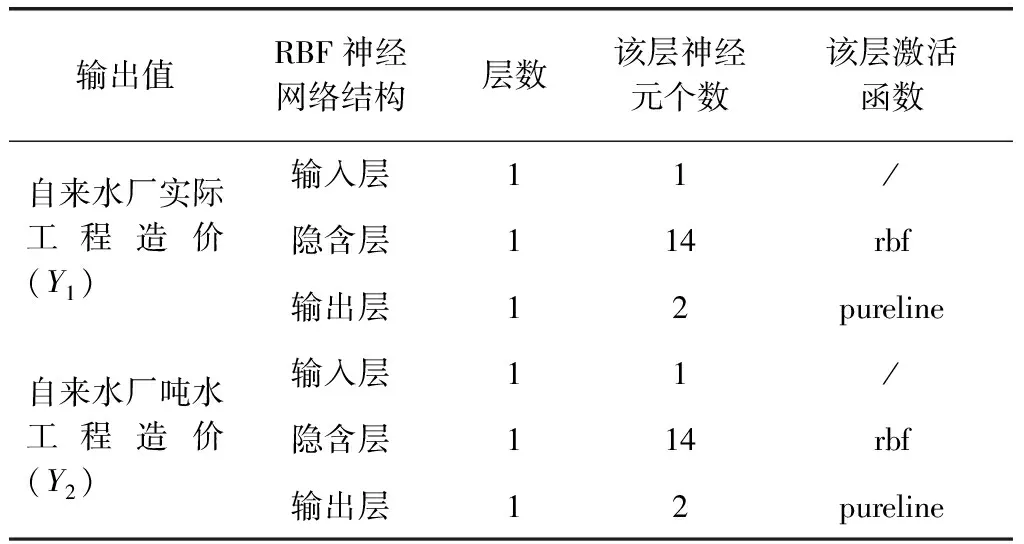
表4 RBF神经网络模型结构Tab.4 Structure of RBF Neural Network Model

通过MATLAB软件构建出的自来水厂工程造价的RBF神经网络模型，拟合曲线如图3、图4所示。其中，虚线代表14组样本的实际工程造价(Y1)或自来水厂吨水造价(Y2)，实线代表基于RBF神经网络模型对14组样本的预测工程造价值，2条曲线的重合程度越高，则代表RBF神经模型对样本数据的拟合程度越好。由图3、图4可知，虚线和实线的重合程度极高，二者几乎完全重合，即代表RBF神经模型对样本数据拟合程度高。

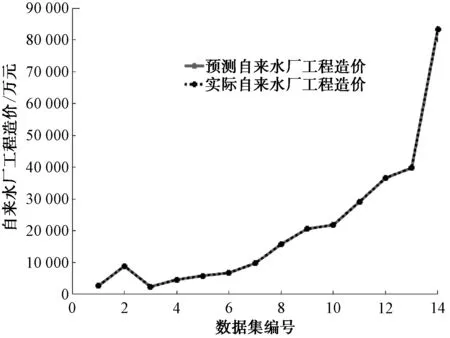
图3 工程造价(Y1)的RBF模型拟合情况Fig.3 Fitting Situation of RBF Model for Construction Costs (Y1)

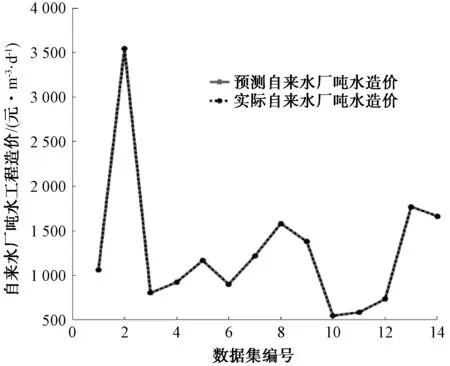
图4 吨水工程造价(Y2)的RBF模型拟合情况Fig.4 Fitting Situation of RBF Model for Unit Construction Cost (Y2)

2 BP与RBF神经网络模型的校验与对比评价

2.1 BP与RBF神经网络模型的实例校验

使用MATLAB软件构建的基于BP和RBF的造价模型，是建立于14组训练样本之上的一类特殊“经验”模型，而非理论推导模型，因此，需通过实际案例数据的检验，以判断人工神经网络模型的准确性。

本研究中使用训练样本以外的4组样本作为测试数据，代入神经网络模型中，可得到自来水厂工程造价(Y1)和自来水厂吨水造价(Y2)2项输出值的预测结果，结合工程的实际值可计算模型的预测误差。校验结果如图5、图6所示。

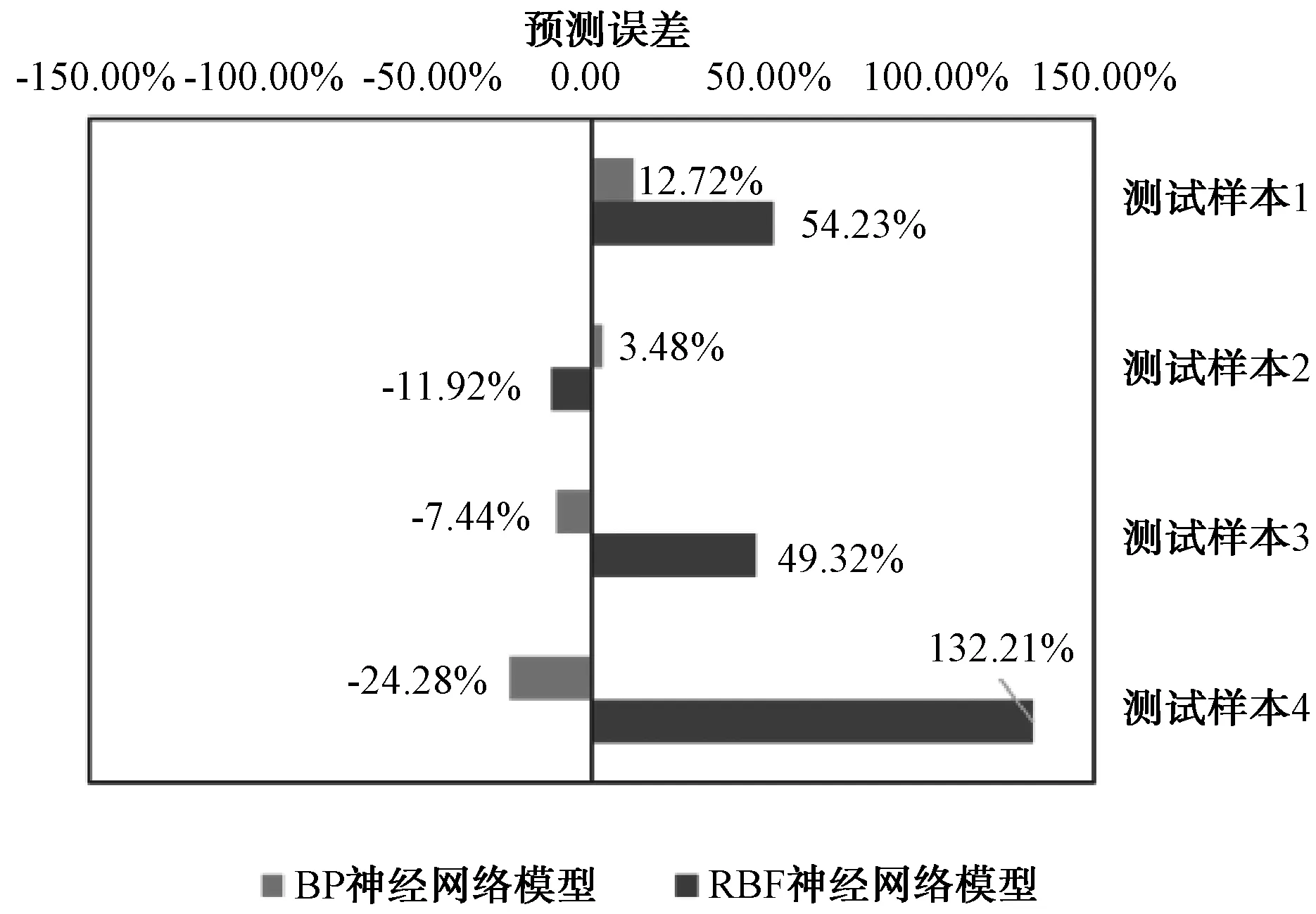
图5 水厂项目工程造价(Y1)的模型校验结果Fig.5 Verification Results of ANN Model (Y1)

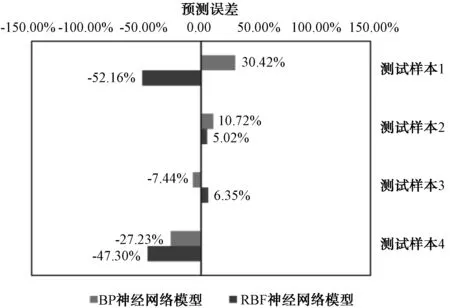
图6 吨水工程造价(Y2)的模型校验结果Fig.6 Verification Results of ANN Model (Y2)

由图5、图6可知，对于2项指标Y1和Y2，BP神经网络模型的测试样本预测误差均可控制在±30%或更低，且5/8的测试样本可将误差控制在±20%，预测效果在项目早期阶段，认为是可以接受的；而对于RBF网络模型，仅有3/8的测试样本误差小于±15%，且5/8的测试样本误差接近或超过±50%，误差过大，通常无法接受。

2.2 BP与RBF神经网络模型的对比评价

由图1～图4的模型拟合结果可知，RBF神经网络模型对于训练样本数据的泛化能力要强于BP神经网络模型，模型预测曲线几乎完全贴近样本数据的实际值。但由图5和图6的对比结果可知，对于自来水厂工程造价(Y1)和自来水厂吨水工程造价(Y2)2项输出值，BP神经网络模型的估算精度远远优于RBF神经网络模型，且预测稳定性更高。与RBF神经网络仅具有1个可调参数相比，BP神经网络的构建过程需要定义多种类型的参数和确定神经网络的结构等，构建过程相对更加困难。

本研究中得到的预测精度结果与刘婧等[6]的模型验证结果相反，对于RBF神经网络模型的预测误差远大于BP网络模型的结果，可能原因如下。

(1)样本数据量较少。RBF网络模型对样本泛化能力过强，反而易受到样本中极端值的影响，导致模型误差率变高。

(2)BP神经网络模型在构建过程中，除模型本身的学习训练外，还经过了多次网络结构的手动调整，以提高其准确度。因此，BP神经网络模型相对更稳定且精确度更高。

3 结论

本研究采用人工神经网络技术构建了基于BP算法和RBF算法的自来水厂工程造价模型。针对水厂建设项目的造价特性，筛选出18个相关影响因素作为输入变量，通过对已有训练样本的学习，构建神经网络模型。其中，基于BP算法的人工神经网络模型具有较好的预测能力，87.5%测试样本的校验结果表明，均可达到项目建议书阶段的估算精度要求(±30%)，50%以上的样本可以达到可行性研究报告的估算精度要求(±20%)。随着累计案例数目的增加，该模型或算法的精确度会不断提高。基于RBF算法的人工神经网络模型估算精度较差，仅有3/8的样本可以达到项目建议书阶段的估算精度要求(±30%)，无法满足实际的工程需求。