测量二次电子空间分布特征矩阵法的有效性分析

孙晓阳，温凯乐，王鹏程，刘瑜冬，黄 涛，刘盛画，刘渭滨，董海义

(1.中国科学院 高能物理研究所，北京 100049；2.散裂中子源科学中心，广东 东莞 523803；3.中国科学院大学，北京 100049)

目前材料二次电子角度分布一般采用理论模拟及实验测量的方法进行研究。在理论模拟方面，大多采用唯象模型及蒙特卡罗模拟的方法进行计算分析[12-13]。而在实验测量方面主要采用3种方法进行测量：1) 能谱仪法[14]，该方法的优点是可测量得到某一能量区间内的角度分布情况，但电子枪和样品旋转会引入较大实验误差；2) 位置灵敏探测器法[15]，其基本原理是给探测器背面上的高阻层加高电压，测量输出信号的幅度得出探测粒子的位置，其缺点是位置灵敏探测器加工工艺要求较高，物理结构和电子学系统复杂，且信号处理需要的放大器易引入较大噪声，影响测试数据的准确性；3) 移动相对位置探测器法[16]，其优点是在测量范围内二次电子空间分布测量精度较高、计算过程简单，但二次电子发射角度分布测量的角度范围(20°～60°)较小，实验过程中移动样品台也会引入一定的实验误差。为精确测量二次电子角度分布，同时增大材料二次电子角度分布测量范围，避免移动样品台带来的实验误差，本文提出一种测量材料二次电子发射角度分布的新方法。

1 设计结构与实验方法

1.1 设计结构

二次电子空间分布测量装置结构示意图如图1所示，其由电子枪、样品台、栅网、四分之一球面收集极、半球形收集极、转动结构等组成。其中电子枪用于提供不同能量的一次电子束流，并垂直入射在样品台上，产生二次电子束。样品台用于固定样品，其上表面的圆心与收集极的球心相重叠，且上表面法线方向与一次电子入射方向平行。半球形探测器外部采用3层结构，且球心相互重叠。最内层为栅网，在栅网及样品台上施加零电压，通过使用运算放大器的虚短效应，使栅网和样品台间接接地，这样可保证栅网和样品台0 V电势，一次电子入射及二次电子产生的过程是发生在等电势环境下，避免收集极上的电压对该过程产生干扰，同时还能测量其电流。中间层为带旋转机构的四分之一球面收集极，空间张角为π，且施加+50 V的偏压，以确保对二次电子的收集效率，且该结构可沿转动轴转动，转动步长可调，从而满足出射二次电子角分布的测量精度。最外层为半球形收集极，空间张角为2π，该半球位置固定，不可旋转，且施加有与四分之一球面收集极相等的电压，该结构用于平衡栅网外的电场分布，避免因四分之一球面收集极上正电压的吸引作用，将其他角度出射的二次电子收集，从而导致角度分布测量不准，同时该半球形收集极结构也可用于收集其余部分的二次电子，并与四分之一球面收集极获得的测量结果进行比对、修正，从而进一步验证该系统的测量准确性。转动结构的转动轴位于样品台上表面的延展面上，且与收集极的球心相交，同时转动结构与两层收集极均相互绝缘，以避免影响收集极对出射二次电子的收集范围。

图1 二次电子空间分布测量装置结构示意图Fig.1 Structural diagram of secondary electron spatial distribution measurement device

1.2 实验原理

本方法测量的二次电子的角分布仅为一次电子垂直入射下的角分布，且测量的样品表面各向同性。通过对称性可知，出射二次电子在φ方向是旋转对称的，仅在θ方向存在差异，且出射二次电子仅分布在样品台的上半平面。因此本方法假设出射二次电子在φ方向是不变的，仅测量其在θ方向的角分布。

通过自由度分析可知，当四分之一球面收集极沿y轴旋转的最小步长为90°/n时，可测量得出的出射二次电子沿θ方向的角分布的最小精度也为90°/n。因此，可将出射二次电子的空间角分布沿θ方向划分为n个区域，如图2所示。

图2 区域划分示意图Fig.2 Schematic diagram of regional division

假设最终测量得出的角分布为矢量R，则R满足：

(1)

其中：rα为在θ=α·90°/n(α=1，2，3，…，n)区域内单位角度二次电子电流。则当四分之一球面收集极的转动角度为θ′=β·90°/n时，四分之一球面收集极上测量到的二次电子电流是由每个区域电流相加得到，而四分之一球面收集极覆盖的范围占每个区域的比值可由计算得到。所以假设存在特征矩阵Sβ：

(2)

其中：sα为四分之一球面收集极转动到θ=α·90°/n角度时，所占区域θ′∈((β-1)·90°/n，β·90°/n)面积与该区域总面积的比值并乘以该区域所占角度(90°/n)。可知，假设当四分之一球面收集极的转动角度θ′=β·90°/n时，四分之一球面收集极上测量得到的二次电流Iβ存在关系：

(3)

对于整个测量过程(β=1,2,3,…,n)，存在特征矩阵S为：

(4)

同时将四分之一球面收集极在不同旋转角度θ′下测得的二次电流Iβ列为矩阵形式，则可得：

(5)

所以存在关系式I=S·R，即：

(6)

通过计算机可方便地对S矩阵求逆得到S-1，则存在关系R=S-1×I。通过对S-1矩阵的计算及对I矩阵的测量，便可通过简单的矩阵乘法得到二次电子的出射角度分布矩阵R。在实验前计算1次S-1矩阵即可，S-1矩阵的值仅与四分之一球面收集极的旋转最小步长相关，每个测试精度下均具有唯一确定的S-1矩阵。同时该测量方法也证明其测量精度是可任意调节的。

1.3 特征矩阵计算

首先计算S矩阵，S矩阵中每个元素sβ,α代表四分之一球面收集极转动到θ=α·90°/n角度时，所占区域θ′∈((β-1)·90°/n，β·90°/n)面积与该区域总面积的比值并乘以该区域所占角度(90°/n)，如图3中a区域所示。

a——计算目标区域(红色区域)；b——计算目标区域所在区间(两条绿线所夹区域)图3 矩阵元素计算示意图Fig.3 Schematic diagram of matrix element calculation

为方便积分，x、y轴沿水平方向，z轴沿竖直方向，建立球坐标系，θ为天顶角，φ为方位角。沿z轴方向，垂直于z轴的平面与球面相交得到的圆半径为R球sinθ，微分面积可表示为dS=R球dαR球sinαdθ。当四分之一球面收集极的转动角度为θ′=β·90°/n时，θ=α·90°/n角分布区域(θ∈((α-1)·90°/n,α·90°/n))上覆盖的面积sβ,α可表示为：

(7)

(8)

当0≤α·90°/n<β·90°/n≤90°时，θ=α·90°/n角分布区域在覆盖区域的上方，这个角分布区域被覆盖的面积sβ,α=0，此时0≤α<β≤n。因为S矩阵中每个元素实际为测量范围占总范围比值与每一区域所占角度的乘积(90°/n)，则：

(9)

使用计算软件进行计算可得S矩阵每个元素的值，然后计算S矩阵的逆矩阵S-1。

1.4 测量过程

1) 求目标矩阵。根据实验需求选择测量精度(如3°)，根据测量精度，使用计算软件进行计算得到S矩阵，并计算得到逆矩阵S-1。

2) 实验测量二次电流。四分之一球面收集极旋转到起始位置，此时探测器上边沿处于竖直状态，电子枪发射电子束，使用皮安表测量四分之一球面收集极收集的电流，并记录为I1。四分之一球面收集极旋转1个精度步长(如3°)，记录皮安表测量的电流为I2。四分之一球面收集极连续旋转，记录收集极处于不同位置皮安表测量的电流I3～In。

3) 数据处理。将测量到的1组二次电流测量值与目标矩阵S-1运算，得到二次电子空间分布测量结果。

2 有效性分析

2.1 模拟结果

使用计算软件进行计算可得I矩阵每个元素的值。模拟过程是假设一种二次电子发射系数关于θ分布的函数形式f(θ)，对其进行积分，得到每个角度下收集的电流：

(10)

(11)

表1为3组假设函数不同精度下的平均相对误差，可看出，该方法测量二次电子角度分布误差较小，精度较高。

2.2 结果分析

本方法假设垂直入射条件下的二次电子空间分布仅在θ方向存在差异、沿φ方向各向同性，使用计算软件计算了特征矩阵，并假设了不同分布函数验证该方法的可靠性，发现不同分布函数在同一精度下的平均相对误差较接近(表1)；而同一分布函数随测量精度的提高，平均相对误差逐渐减小。在实际实验过程中，可通过提高测量精度来减小实验误差。仿真测试结果与理论值的对比发现，二次电子分布的测量值在接近θ=0°时发生偏差(图4)，是因为θ接近0°时，分割单元面积较小，在求解过程中面积小的单元引入的误差较大，说明该方法在获得θ接近0°时的数据存在一定误差。

表1 3组假设函数不同精度下的平均相对误差Table 1 Average relative error of three hypothesis functions with different accuracies

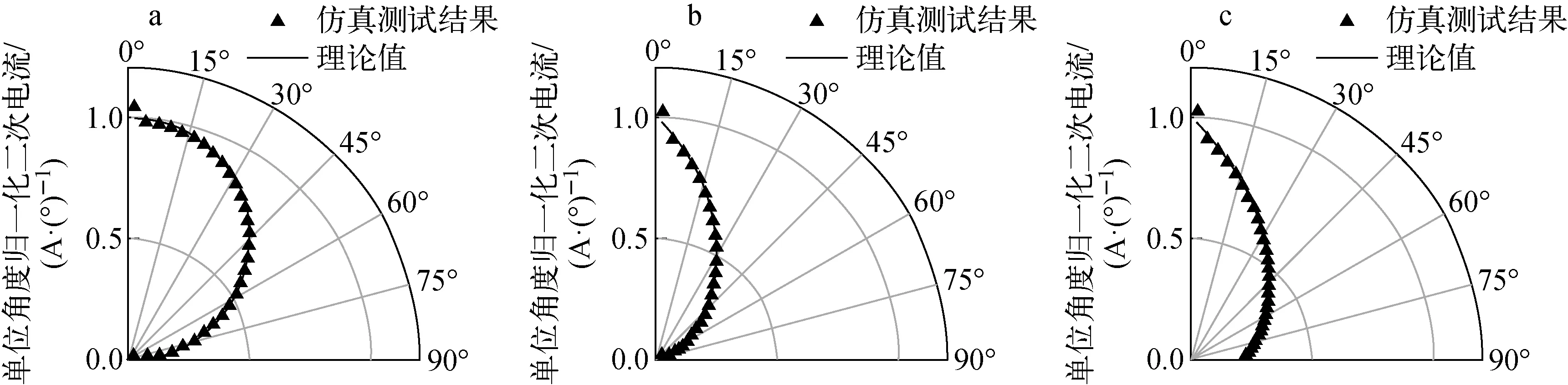
a——f(θ)=δ0cos θ；b——f(θ)=δ0(1-sin θ)；c——f(θ)=δ0e-θ图4 二次电子空间分布理论值与测量值的对比Fig.4 Comparison between theoretical and measured values of spatial distribution of secondary electron

3 结论

本文提出了探测器的物理设计，通过计算模拟对测量方法进行了校验，模拟结果与假设二次电子空间分布函数相吻合，表明该测量方法可靠、测量精度高，从而验证了测量方法的有效性。该测量方法的优点为：1) 计算过程简便，将测量得到的电流与特征矩阵运算，即可得到二次电子发射空间分布；2) 测量精度可调节，在不对设备结构进行更改的情况下，可根据实验需要调节测量精度；3) 信噪比高，测量得到的二次电子信号强，有利于降低暗噪声的干扰；4) 仅需4个电极便可引出测量信号，电路方面相对简单稳定且可靠。不足之处是球面探测器结构较为复杂，加工难度较大。

目前对测量方法的可行性检验，是假定几种可能的二次电子空间分布，计算得到模拟的电流信号，根据电流信号反向计算得到了二次电子的空间分布，与原始假设一致。在验证计算过程中，对真实测量过程中可能存在的各种误差(如入射一次电子的空间分布的影响、散射一次电子的影响等)分析不足，对于测量偏差和准确度的估计可能不充分。在下一步的工作中会结合实验结果，进行更深入的分析和修正。