基于卷积-反卷积网络的正交人脸特征学习算法

孙文赟，宋 昱，陈昌盛

深圳市媒体信息内容安全重点实验室，广东省智能信息处理重点实验室，深圳大学电子与信息工程学院，广东深圳518060

深度神经网络(deep neural networks, DNN)已在多种计算机视觉任务中获得成功应用，尤其是人脸表情识别与人脸识别任务.从数据中学习深度人脸特征是一种常见的做法，研究者通过设计不同的网络结构和训练方法获取具有不同性质的人脸特征.这些可学习的深度特征具有比传统图像特征更好的性质.例如，在人脸识别任务中，一个训练良好的身份特征对人脸的姿态、人脸表情、年龄和配饰具有不变性.类似地，在人脸表情识别任务中，表情特征对人脸的姿态、身份具有不变性.而在最新的域自适应算法中，训练良好的跨域特征可对域偏移具有不变性.

基于深度特征学习理论，SUN等[1]使用一对卷积-反卷积神经网络学习了身份特征与表情特征两组正交的人脸特征.其中，身份特征对表情的变化不变，而表情特征对身份变化不变.但是，该方法在特征学习过程中需要一对含表情的人脸和中性人脸，后者作为监督信息，用于定义同身份但不同表情的人脸图像的统一锚点.此外，该方法还需对每个身份分别记录7种表情(生气、恶心、恐惧、高兴、悲伤、惊讶和中性)的人脸图像.然而，主流的人脸识别数据集仅包含身份特征，并无关于表情的标签，少数的人脸表情识别数据集虽同时具有身份与表情标签，却并没有为每个身份提供对应的中性人脸.本研究为解决以上在联合学习过程中缺乏训练数据的问题，扩宽人脸身份与表情正交特征联合学习算法的应用范围，基于文献[1]方法，引入相关性最小化损失来缓解训练时对中性人脸的依赖，通过构建一个卷积-反卷积神经网络，在已对齐人脸图像上提取身份与表情特征，并采用重构损失、分类损失和相关性最小化损失组合训练目标.本研究首次使用了表情标签学习身份特征，将新方法记为无监督正交人脸特征学习(unsupervised orthogonal facial feature learning, UOFFL)算法，而将文献[1]方法记为有监督正交人脸特征学习(supervised orthogonal facial feature learning, SOFFL)算法.在大规模合成人脸表情数据集(large-scale synthesized facial expression dataset, LSFED)[1]与受限的Radboud人脸数据集(Radboud faces dataset, RaFD)[2]上的人脸特征学习结果表明，UOFFL算法的性能超越了一些无监督算法，且接近SOFFL等有监督算法.

1 基于深度特征分解的人脸特征学习

正交人脸特征学习方法将人脸特征分解为身份、姿态、表情和背景等部分，从任务角度来看，UOFFL算法与人脸特征分解[1,3-8]有关；从损失与优化角度来看，UOFFL算法中的相关性最小化损失与基于协方差对齐和最小化的域自适应算法有关[9-12]，因为它们均通过优化来调整神经网络特征的分布，实现了特征的二阶统计量调节.

1.1 可分解深度特征学习

将深度人脸特征分解为身份、姿态、表情和背景等属性，一方面可从图像数据中学习、提取并分解不同的深度特征；另一方面，图像可从分解后的特征中重构和生成[1,3-8].现有的可分解深度特征学习方法大多采用卷积神经网络提取特征，并使用反卷积神经网络重构和生成图像，也有采用基于对抗学习的生成模型[3-6].TRAN等[3]和ZHANG等[4]分别提出可分解特征学习生成对抗网络和条件对抗自编码器.这两个网络将人脸分解为身份特征与姿态或年龄特征，并根据给定特征生成新的人脸图像.MA等[5]将行人图像分解为前景特征、背景特征与姿态特征，并根据给定特征生成新的行人图像.BERTHELOT等[6]提出一种对抗受限自编码器插值的新型损失，可提高合成人脸的真实感和插值特征的语义连续性.还有一些基于判别模型的图像重构方法[1, 7-8].ZHU等[7]使用非确定性神经元来采样随机的姿态特征，提出一种非确定性神经网络用于建模人脸、身份与姿态的关系.DOSOVITSKIY等[8]用反卷积神经网络学习属性到图像的函数映射.本课题组2018年提出的SOFFL算法[1]亦属于可分解深度特征学习范畴.

1.2 有监督正交人脸特征学习

SOFFL算法从已对齐的人脸图像中提取身份特征与表情特征，训练样本为三元组(X,y,Z).其中，X为被提取特征的原始含表情人脸；y为真实表情标签；Z为对应于原始含表情人脸的中性人脸，X和Z具有相同的身份和不同的表情.在一些任务中，中性脸Z很难获取，因为主流的人脸识别数据集仅拥有身份标签，即使有些人脸表情识别数据集同时具有身份和表情标签，但也并非每个个体都有中性脸图像，训练数据要求过高是SOFFL算法的主要缺点.

1.3 基于二阶统计量调整的域自适应方法

二阶统计量调整是域自适应领域的主流方法之一[9-12].其中，协方差对齐算法定义为

(1)

其中，A为对齐源域和目标域特征的协方差的线性变换；xs与xt分别为源域和目标域的样本域特征；函数cov()计算协方差矩阵.文献[9]给出了式(1)的闭式解.

在神经网络网络中，协方差对齐问题常转化为

(2)

其中，神经网络fθ受可训练参数θ控制；fθ(xs)和fθ(xt)分别为待对齐的源域特征与目标特征的激活与目标激活，优化可使它们的分布在源域和目标域中一致.式(2)常配合卷积神经网络的主要目标进行联合训练[10-12]，等价于最小化带有二次多项式核的最大均值差异(maximum mean discrepancy, MMD)[11, 13-14].协方差对齐与核MMD均为用于神经网络的域自适应的主流算法.

另一种二阶统计量对齐方法为协方差最小化.BOUSMALIS等[11]提出基于二阶统计量的损失用于鼓励神经网络特征的各维度之间的分布差异：

(3)

其中，x为输入样本；fθc和fθp分别是计算公共特征集和私有特征集的神经网络.若fθc(x)和fθp(x)均已中心化，则式(3)等价于最小化两个特征集合之间的两两协方差

(4)

这些域自适应方法初步验证了对神经网络激活的二阶统计量的调整的可行性.

1.4 无监督人脸验证

LIAO等[15]提出的无监督特征学习算法，可从一组姿态连续变化的人脸视频中学习人脸光照与姿态不变的特征.该方法将相同身份的人脸分组在同一视频或集合中，分组被视为身份监督的一种变形.UOFFEL算法则是从特征的互补性角度出发，因并未使用任何形式的身份监督，对训练数据要求更低.

2 无监督正交人脸特征学习

2.1 深度神经网络结构

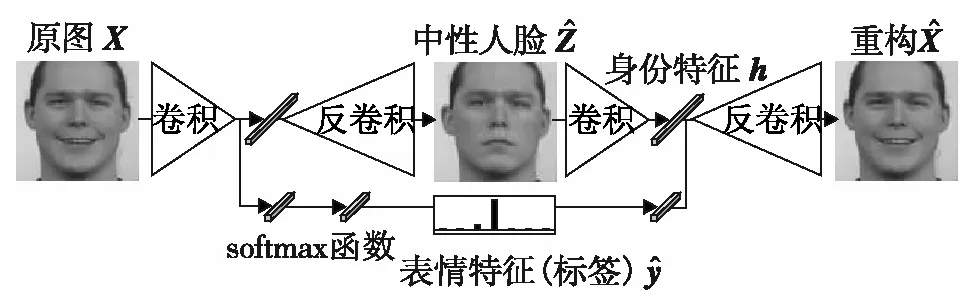
图1 SOFFL的网络结构[1]

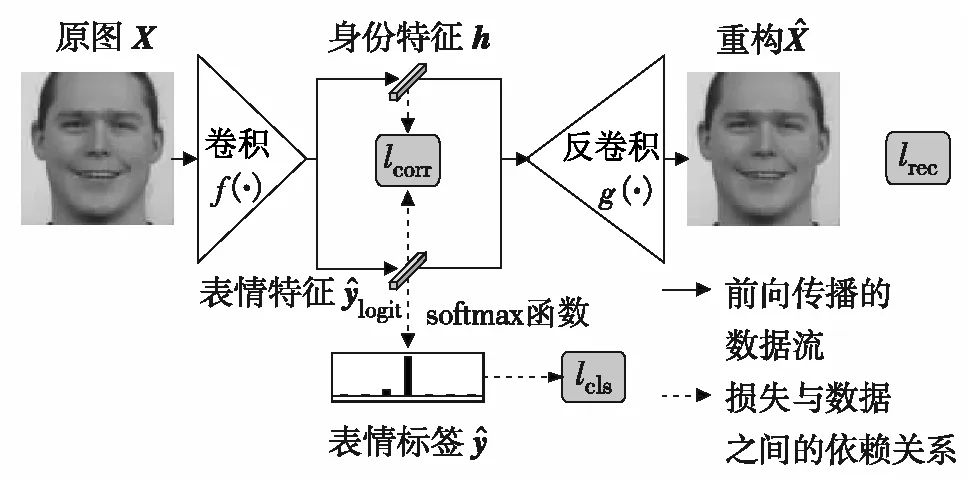
图2 UOFFL的网络结构

在图2中，lrec为重构损失；lcls为分类损失；lcorr为相关性最小化损失.假设算法的已对齐人脸图像中仅存在身份和表情两种变化，则在前向传播中，卷积层将人脸图像编码为身份和表情特征，而反卷积层从特征中重构输入的人脸图像.

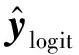
(5)

则网络的前向传播为

(6)

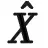
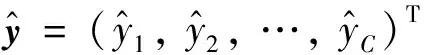
(7)

本研究参考VGG网络的设计思路，采用若干3×3卷积层后附一个下采样层组成的基础结构，再由若干基础结构构成网络.表1展示了UOFFL网络的层类型、层激活个数和层参数个数等细节，整个网络是由一个卷积部分和一个反卷积部分组成，其中卷积部分包含6个VGG基础结构，将尺寸为64×64×1像素的输入图像变换为1×1×519像素的全局向量形式特征；而反卷积部分也包含6个VGG基础结构，其中后置下采样层替换为前置上采样层.反卷积部分将1×1×519像素的特征变换为64×64×1像素的图像.当输入尺寸、中间特征个数和输出尺寸确定时，表1中的细节可按VGG网络的基本规则生成.

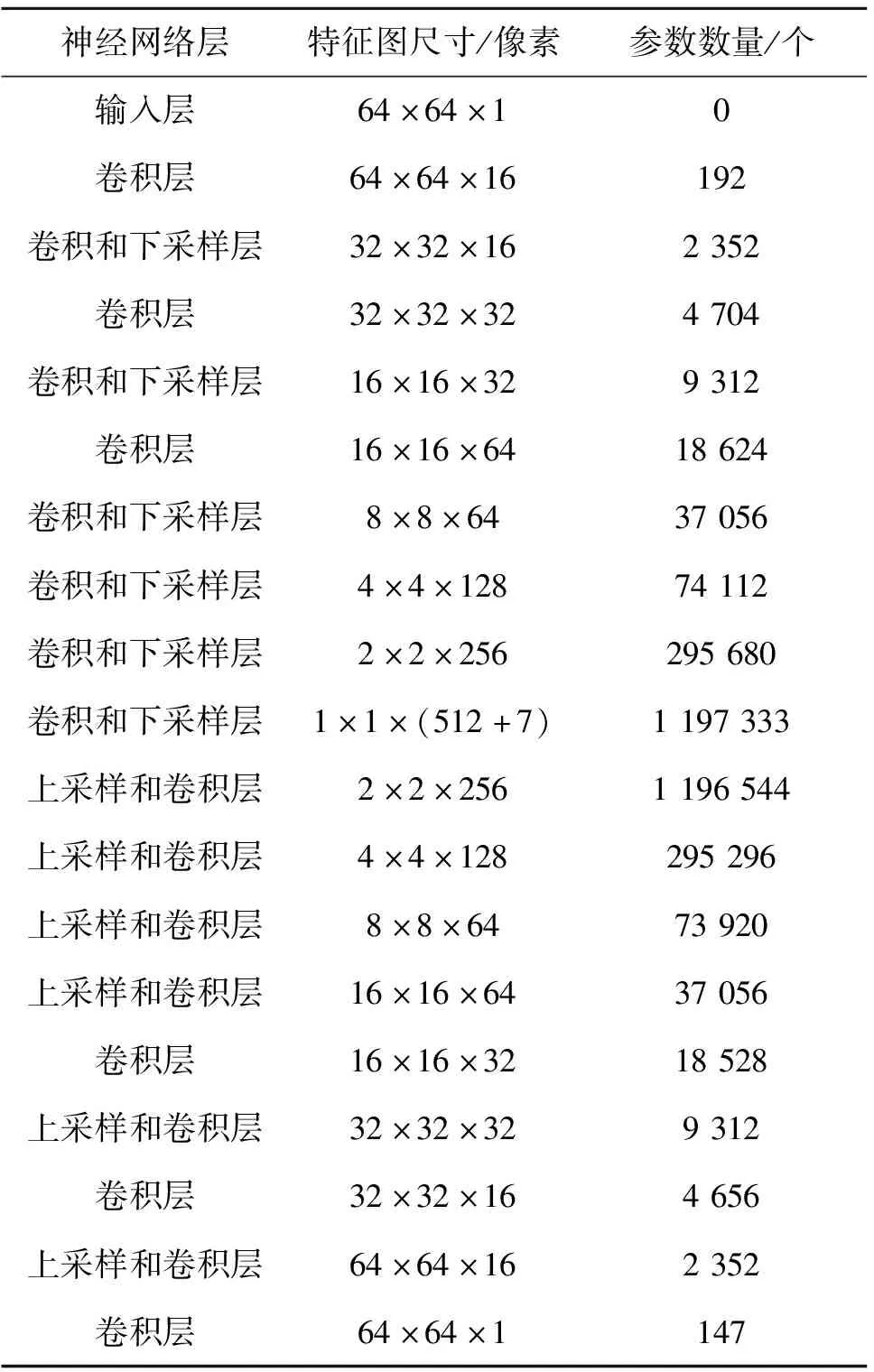
表1 UOFFL的网络细节

使用批归一化(batch normalization, BN)、激活函数tanh()和平均池化下采样法来确保网络激活的是标准正态分布.归一化激活分布不仅可加速训练还可简化相关性最小化损失中的皮尔逊相关系数(Pearson correlation coefficient, PCC)的计算.每个卷积层使用BN归一化和tanh()激活.整个网络共包括了18个卷积层，不含任何全连接层，网络共有约328万个可训练参数，网络的规模远比一些常见网络小，但已足够达到提取正交特征、重构原始人脸的要求.

2.2 损失函数

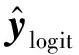
(8)

其中，E()和σ()分别为期望值与标准差函数.因此，两组随机向量a=(a1,a2, …,am)T和b=(b1,b2, …,bn)T之间的皮尔逊相关矩阵可定义为

ρ(a,b)=

(9)

PCC是一种归一化的协方差，值域为[-1, 1]，相比协方差矩阵，它对随机变量的尺度具有不变性.基于皮尔逊相关矩阵的相关性最小化损失为

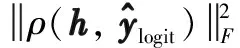
(10)

该损失在计算上等价于两两PCC的平方和，即

(11)

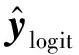
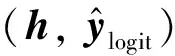
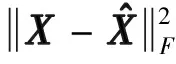
(12)

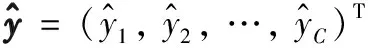
(13)

假设人脸空间中仅有身份和表情两种变化，则分类损失lcls用于学习表情特征y；重构损失lrec用于确保信息完整性；相关性最小化损失lcorr提升两组特征之间的独立性.总体损失为三者的加权和

ltotal=lrec+λ1lcls+λ2lcorr

(14)

其中，非负权重λ1和λ2用于平衡3个分量的重要性.

3 实验与结果分析

3.1 数据集与预处理

采用LSFED[1]与RaFD[2]数据库验证UOFFL算法的性能.由于LSFED数据库中的图像由软件合成，不含噪声且对齐精准，导致所有对比算法的性能都趋于饱和，无法区别算法优劣，故提升难度以模拟复杂的真实世界环境，给数据集加入SNR=20 dB的高斯噪声，并将加噪的数据集记为LSFED-G.根据文献[15]方法构造包含高斯噪声和随机相似变换的数据集，记为LSFED-GS；构造包含高斯噪声、随机相似变换和随机背景的数据集，记为LSFED-GSB.

RaFD是一个在受限环境下采集的小规模人脸表情数据集，仅包含67个个体，每个个体有8种表情、5种姿态和3个眼睛注视方向信息.为保持数据集的一致性，本实验仅使用眼睛直视的正面脸图像，并丢弃轻蔑表情的图像，最终剩下469张人脸图像.在处理中，首先使用基于方向梯度直方图(histogram of oriented gradient, HOG)特征与支持向量机(support vector machine, SVM)的人脸检测器检测人脸包围盒；然后检测68个人脸特征点[17]，估计人脸形状与姿态[18]；最后将人脸图像对齐到预定义的三维人脸几何体上，再渲染和裁剪出尺寸为64×64像素的人脸图像.图3为部分预处理后的人脸.

图3 部分预处理后的LSFED与RaFD数据集人脸

两个数据集大致按照8∶2的比例划分为训练集和测试集，且其中的人脸所属的身份不重合.

3.2 训练模型

采用文献[19]方法初始化网络的卷积核，偏置被初始化为0，BN中的均值和标准差的滑动平均初始值分别设为0和1，采用自适应矩估计(adaptive moment estimation, ADAM)优化器训练网络，优化器参数设置为α=0.001、β1=0.9、β2=0.999，ε=1×10-8.使用随机梯度下降方式最小化总体损失.训练集先被随机打乱顺序，每次迭代依次送入100个训练样本，每个训练样本均参与训练100次后终止训练.为评价3个损失分量对识别结果的影响，采用不同的λ1和λ2值，当λ1=λ2=0时对应的损失分量不发挥作用.

3.3 无监督人脸验证对照实验结果分析

基于已训练的网络，使用人脸验证任务评价学得的身份特征h的性能.随机抽取1 000个正样本对(相同身份但不同表情)和1 000个负样本对(不同身份但相同表情)，计算样本对在身份特征空间中的欧氏距离，并选取合适的阈值.若两个人脸的距离大于阈值则判别为不同身份；若小于阈值则判别为相同身份.选取的接收者操作特征曲线上面积(area under the receiver operating characteristic curve, AUC)和等错误率(equal error rate, EER)评价指标与阈值无关，在应用中可选取训练集上距离的中值作为人脸验证的阈值.表2展示了不同数据集在不同空间欧氏距离中采用无监督人脸识别所得AUC和EER值.由表2可见，UOFFL算法在LSFED、RaFD和加噪的数据集上工作良好，在相对干净的LSFED、LSFED-G与RaFD数据集上，取λ1=1，λ2=1时可获得较好的结果，而在有严重噪声的LSFED-GS与LSFED-GSB数据集上，取λ1=1，λ2=10，适当提高相关性最小化损失的作用，提升身份特征与表情特征之间的独立性，可获得较好的身份特征，进而获得更好的人脸验证性能.

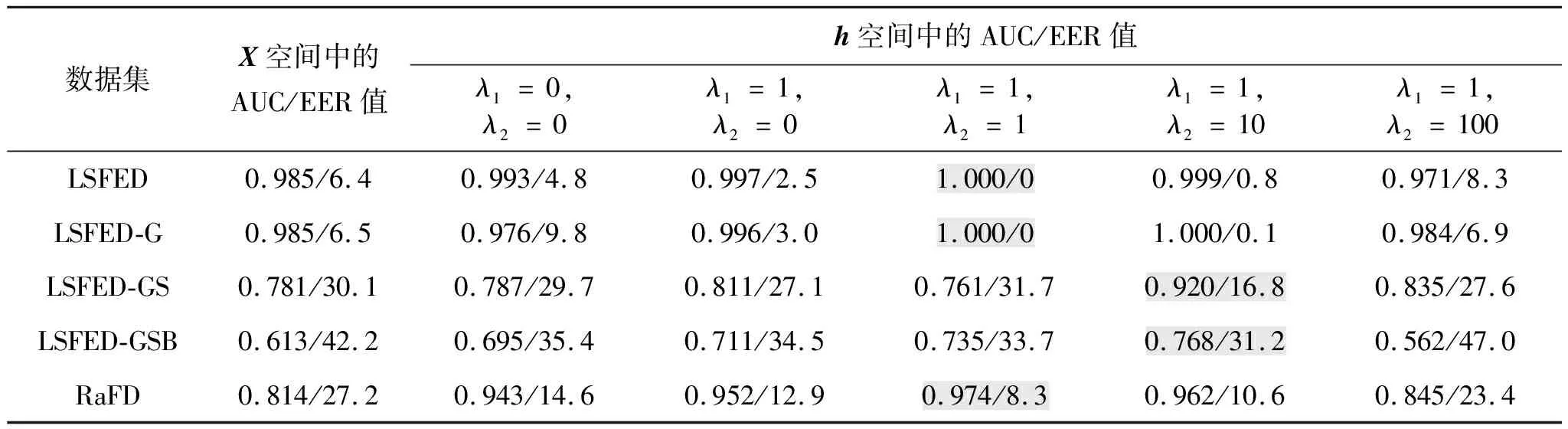
表2 基于不同空间欧氏距离的无监督人脸识别性能结果1)

表2第2列X空间中的AUC和EER值是将原始图像拉直为向量后，计算欧氏距离所得的AUC和EER指标结果.第3～7列为不同λ1和λ2取值下UOFFL算法的AUC和EER指标结果，使用特征学习可以获得比原始图像上更好的结果.对比第3～6列可以发现，启用相关性最小化损失，并选取合适的权重可分别在LSFED、LSFED-G、LSFED-GS、LSFED-GSB和RaFD数据集上获得0.002 7、0.004 1、0.108 9、0.057 5与0.021 8的AUC指标提升，故UOFFL算法的相关性最小化是解决无监督人脸验证问题的关键.选择合适的λ1和λ2可进一步提升性能，在大多数情况下，取λ1=λ2=1较好，当人脸图像中噪声交大时，可尝试取λ1=1，λ2=10.

3.4 有监督和无监督人脸验证的对比

表3对比了UOFFL算法与其他7种人脸验证算法的AUC指标值.其中，LBP+PCA+LDA[20]、AlexNet预训练+微调[21]、两层神经网络、LBP+PCA+联合贝叶斯[22]和SOFFL算法[1]因训练中使用身份标签属有监督学习；UOFFL算法、原图上的欧氏距离方法、PCA主成分上的欧氏距离方法和文献[14]算法是未使用身份标签的无监督学习.UOFFL算法在相对干净的LSFED、LSFED-G与RaFD数据集上的表现超过或接近有监督学习方法；在噪声较大的LSFED-GS数据集上，UOFFL算法在无监督算法中的表现仍保持最好；而在含有随机背景的LSFED-GSB数据集上，UOFFL算法的性能不佳，这是因为随机背景作为表情特征的互补亦被编码在身份特征中，影响人脸验证效果.LSFED-GSB数据集违背了UOFFL算法人脸空间中仅有身份和表情两种变化的假设，故需根据实际情况选择算法.

表3 有监督和无监督人脸验证方法的性能对比1)

UOFFL算法与SOFFL算法关系紧密，不同于主流的已在人脸基准上获得较好的性能的人脸验证算法，SOFFL算法需要包含表情人脸和同身份中性表情人脸图像对作为训练数据，其训练样本为三元组(X,y,Z).由于对数据要求过高，SOFFL方法无法在野外标签人脸(labeled faces in the wild, LFW)数据库等主流数据集上训练测试，本研究将其训练数据简化为二元组(X,y)，导致UOFFL算法在LSFED-GS与LSFED-GSB数据集上的性能略低于SOFFL方法.然而，在小样本RaFD数据集上，UOFFL算法的确比SOFFL算法略有提升(由0.962提升至0.974)，这是因为SOFFL算法需要学习一个复杂的图像到图像双向映射，这在小样本数据上会比较困难，而UOFFL算法改为学习像素图像到519维特征的双向映射，避免了该问题.

尽管有监督方法比无监督方法因使用更多的数据而获得了更好的性能，但UOFFL算法提出的相关性最小化损失，能够缓解标签缺失的劣势，缩小无监督和有监督方法的性能差距.总体上讲，UOFFL算法性能优于无监督的文献[14]和有监督的SPFFL算法，接近有监督的联合贝叶斯人脸识别算法.

结 语

提出一种基于卷积-反卷积网络的正交人脸特征学习UOFFL算法，使用3个损失训练网络：分类损失用于学习表情特征，重构损失用于确保特征中信息的完整性，相关性最小化损失用于提高身份特征与表情特征之间的独立性，最后，在合成人脸和真实人脸数据集上进行实验验证.下一步，计划将方法拓展到非受限人脸和跨库或跨域问题中.例如，在野外静态面部表情(static facial expressions in the wild, SFEW)数据集上训练，并在LFW数据集上测试，或将LSFED数据集上学得的知识迁移到非受限人脸.