基于3D打印透明微细孔隙模型的多孔介质渗流规律

钱自卫，黄 震，袁世冲

(1.中国矿业大学 资源与地球科学学院，江苏 徐州 221116; 2.江西理工大学 资源与环境工程学院，江西 赣州 341000)

孔隙是石油、天然气、地下水等贮存的主要场所，开展多孔介质渗流规律的研究是进行油、气、水资源开采及水害防治的重要基础性工作[1-3]。其中，孔隙渗流模型试验是开展相关研究的重要手段，但试验要求制备高仿真度的孔隙渗流物理模型。比如，在驱替采油领域常用的一维物理模型主要包括天然岩芯和人造岩芯模型，二维模型主要包括岩芯薄片、玻璃仿真物理模型[4-5]，三维模型主要包括天然露头岩芯、填砂和高温高压烧结而成的人造砂岩模型[6]。一维模型仅适于进行简单试验，而三维模型难以观测到模型内部实时试验现象并获得相应数据，因此，二维模型应用相对广泛。目前常用的岩芯薄片二维模型的原料直接取自天然岩芯，由机器切成薄片后与玻璃恰当黏结而成[7]，其主要的问题是模型制备的复杂性及重复性:一方面,对于胶结程度差的孔隙砂岩，制备岩芯薄片极为困难;另一方面，难以制备多组一致的模型开展多因素对比研究。同样较常用的玻璃仿真二维模型是通过在玻璃模型上刻制孔道来反映真实孔隙结构，常用的为化学刻蚀法[7]。化学刻蚀的本质是借助于氢氟酸对玻璃材面的腐蚀作用实现孔隙的制造，由于腐蚀区域、进度控制技术的制约，同样难以制备与真实岩石一致的孔隙结构。

近年来，随着3D打印(3D Printing，3DP)技术发展及应用，可利用该技术有效解决精细透明孔隙网络物理模型构建的问题。3D打印技术是指在计算机控制下快速制造任意复杂形状3D物体的新型数字化成型技术。目前该技术已迅速在工业设计、机械、医疗、建筑等领域得到应用，其中医疗领域应用最广泛。3D打印技术在国际上已开始被应用于个性化组织工程支架材料的制造、细胞或组织打印等方面，其制备材料的精度可以达到微米级[8-9]。3D打印技术在岩土工程研究方面已有应用的先例，如鞠杨、谢和平等[10-11]在国内首次运用CT成像、三维重构和3D打印技术，利用透明材料成功制备了天然裂隙煤岩模型，精度达到10～50 μm。另外，熊祖强、OTTEN、JIANG、BOURKE、JIANG、胡成果、田威、董茜茜等[12-21]采用3D打印技术制备不同种类的岩土物理模型用于相关试验研究。鉴于此，笔者基于砂层CT图片，构建二维孔隙模型，采用光固化型3D打印机制备透明微细孔隙物理模型，克服当前常用模型不可视、不可批量制备等问题。基于3D打印透明微细孔隙模型，开展多参量对比渗流试验，研究多孔介质渗流规律。

1 透明微细孔隙模型制备

1.1 微细孔隙模型构建

以榆林毛乌素沙漠松散砂层为研究背景，试样取自榆林金鸡滩煤矿副斜井埋深20 m处的松散富水砂岩。对砂层试样通过CT扫描、图片处理、模型构建等步骤，最终构建孔隙模型。

CT扫描利用蔡司三维X射线扫描电镜进行，扫描半径8.02 mm。微细孔隙模型建模过程如图1所示，首先选取典型CT图片，进行图片剪切及二值化处理，然后采用矢量化提取软件，提取砂颗粒边界，最后导入三维建模软件构建基于真实砂层CT图片的二维孔隙结构体。

孔隙结构体构建完成后，再构建孔隙试验模型，如图2所示，孔隙模型整体呈长方体，尺寸(长×宽×高)为25.5 mm×14.2 mm×1.6 mm，包括孔隙结构体、缓冲仓、出入口。孔隙结构体为长方体状，长宽均为8.50 mm，厚度为0.45 mm;缓冲仓分列于孔隙结构体两侧，为半圆柱体形，半径为4.25 mm，厚度为7.40 mm;出入口为圆管状，直径为0.60 mm。

1.2 孔隙模型3D打印制备

微细孔隙模型制备采用光固化型3D打印机，该类打印机主要基于液态光敏树脂的光聚合原理，打印精度一般大幅高于纸层叠法。本研究模型制作具体采用LD-003型3D打印机，打印层厚精度达到±0.002 mm，平面打印精度为0.075 mm。

3D打印选用无色透明状刚性光敏材料，此材料黏度150～300 MPa·s，光敏材料固化后的单轴抗压试验曲线如图3所示，强度可达到63～68 MPa，破裂时应变达到25%～28%，呈现与常规岩石一致的剪切破坏形式。

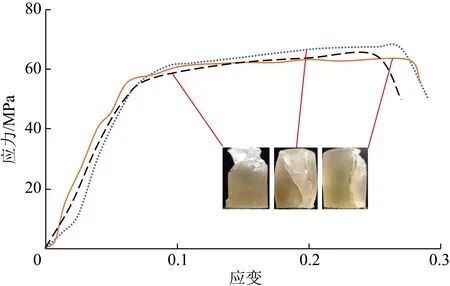
图3 光敏材料固化后的单轴抗压试验曲线Fig.3 Uniaxial compression test curves of photosensitive material after curing

考虑到打印机的平面打印精度，如采用孔隙模型原尺寸打印，部分微细孔隙结构无法识别。在多次逐步放大比例试打印后，最小放大比例为2.1倍时能基本实现孔隙的识别，即实际打印模型尺寸(长×宽×高)为54.0 mm×30.0 mm×3.4 mm，孔隙结构体边长为18.00 mm，厚度为0.96 mm，最终打印的模型如图4所示。

图4 3D打印的孔隙模型Fig.4 3D printing pore model

2 孔隙渗流试验系统及试验方案

2.1 试验系统

孔隙渗流试验系统如图5所示，试验系统包括注水系统、压力监测系统、观测系统、孔隙模型及管路。

图5 孔隙渗流试验系统Fig.5 Pore seepage test system

注水系统由医用微量注射泵及注射器组成，医用微量注射泵型号为HK-400，通过设定注浆泵推进注射器活塞速率来设定注水流量。注浆压力监测系统由压力变送器及数据采集仪组成，压力传感器的量程为0～100 kPa，型号MIK-P300，精度0.01 kPa;数据采集仪器型号为MIK-R5001D型18通道的全自动数据采集仪，数据采集最小密度0.1 s。压力传感器通过量测注射器内在压力来监测注水压力。观测系统由电子显微镜及电脑组成，电子显微镜型号为GP-440H，最大可放大150倍，连接笔记本电脑实现录像及图片采集。管路采用透明硅胶管，硅胶管外径2.0 mm。

2.2 试验方案

试验时孔隙模型水平放置，采用注水流量增加的方式进行多孔介质渗流试验，共设置12个梯度，流量为0.83～25 mL/min，每个梯度试验时间20 s，注水压力采集频率为每秒1次。本次试验共2个试验模型，编号为1号，2号，2个模型的孔隙结构体为呈平面90°的同一孔隙结构体(图1(d))，注水试验时调整注入口，实现同一孔隙结构体从4个不同方向注水(1号左、1号右、2号上、2号下)(图6)。另外，为研究孔隙渗流过程，采用染色水进行饱和孔隙的注水试验，观测孔隙的渗流过程。

图6 孔隙渗流试验监测数据Fig.6 Monitoring data of pore seepage test

为消除注水管路对模型试验的影响，专门进行管路同等流量梯度的注水试验，监测注水压力。模型4个不同方向注水及管路注水试验各进行2次，取平均值，注水监测压力减去管路渗流压力即为孔隙结构体渗流压力。另外，渗流试验过程中，模型孔隙中严防气泡存在，以保证试验结果的准确性。

3 孔隙渗流试验结果分析

3.1 孔隙渗流过程

图7为注水流量为0.83 mL/min，计算渗流速度为1.16 mm/s时孔隙渗流过程观测图片，图片采集时间间隔为1 s。由图7可以看出，在孔隙渗流过程中分流及汇流持续发生。试验孔隙模型的孔隙渗流活跃性差异较大，比如中间及偏上位置渗透阻力较小，渗流活跃;左下区块渗透阻力较大，孔隙渗流滞后明显。此外，由图7可知，部分孔道未参与渗流过程。

3.2 渗流规律分析

3.2.1渗透性与水力梯度关系(k-J分析)

孔隙模型12个连续注水流量梯度测试结果如图6所示，由于每个注水流量后半程10 s段监测水压较为平稳，以此阶段计算平均渗流压力及水力梯度J，采用达西定律计算模型的渗透系数k，结果如图8所示。由图8可以看出，随着J的增大，k整体呈现下降趋势，两者关系可用幂函数拟合(相关系数R2>0.88)，且J越大相关性越强。对比4个不同注水方向结果可知，在低J条件下，左右方向注水k相对高于上下方向，随着J的增加，4个不同注水方向的k均呈现幂函数特征。

3.2.2渗流速度与水力梯度关系(v-J分析)

图9为渗流水力梯度J与渗流速度v的关系图，v与J呈显著的二次函数关系，可用式(1)拟合，4个不同渗流方向下，相关性系数R2均大于0.997。对比来看，同一模型调换注入口，相同v时，J差异较小;1号、2号两个模型对比看，相同v时，J差异较大。

J=av+bv2

(1)

式中，a，b为待定系数。

式(1)即为1901年P.Forchheimer提出流速v与水力梯度J之间的非线性关系式。对于理想情况，当渗流为层流时，系数b=0，J=av，即渗流满足线性达西流定律;反之，当渗流为紊流时，系数a=0，J=bv2[22]。由试验模型v与J拟合关系可知，模型在本试验条件下可认为层流及紊流并存(复合流)。如J′=bv2设定为紊流惯性力对J贡献，则随着v的提高，J′占J的比例逐渐提高(图10)。

图10 孔隙渗流模式分析曲线(以2号下模型为例)Fig.10 Analysis curves of pore seepage pattern(Take the No.2-down model as an example)

多孔介质渗流水流状态与雷诺数密切相关，低雷诺数时，为黏滞性占优势的层流，适用于达西定律;高雷诺数时为紊流运动[22]，但已有研究成果获取的雷诺数界限值一直不精确[23]。从图9，10及式(1)分析认为，模型渗流试验为层流+紊流的混合流，分析认为这可能与多孔介质的孔道结构有关。孔道结构分为孔隙及吼道，孔隙通过相对狭窄的喉道相连，喉道是孔隙介质渗流性能的关键因素，图11为多孔介质典型孔喉结构。

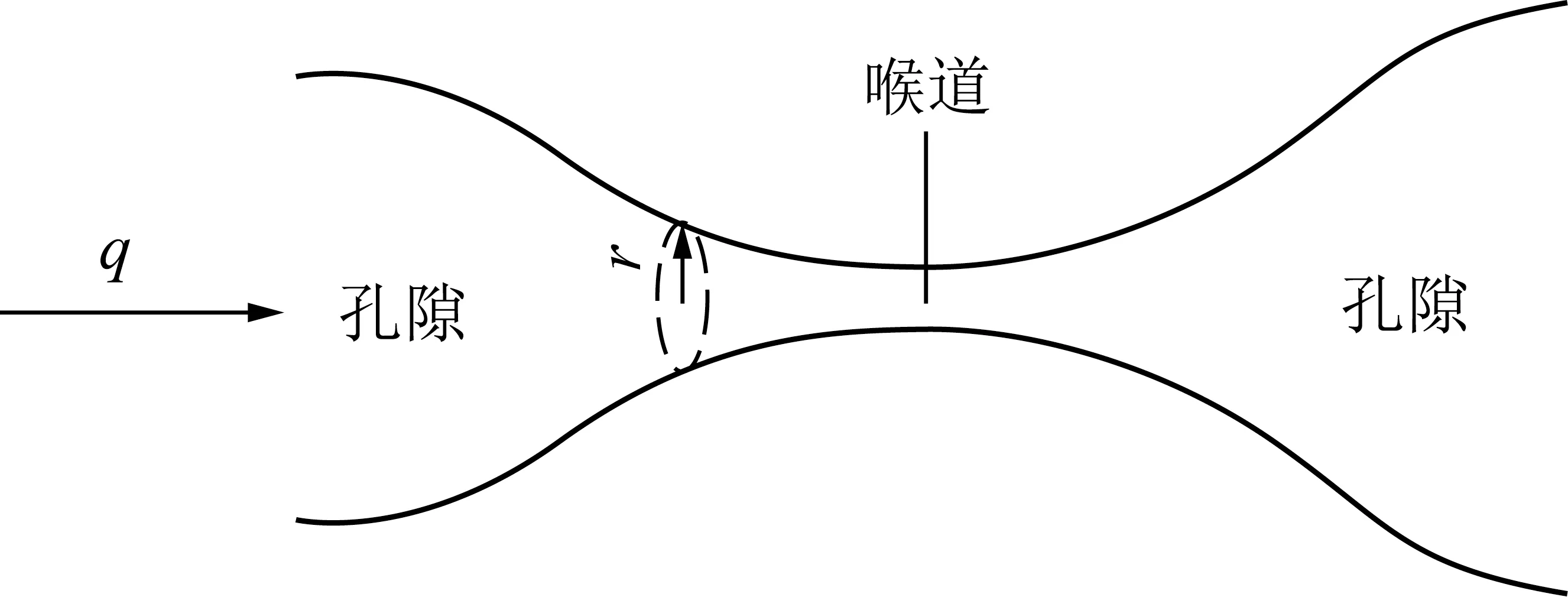
图11 典型孔道结构Fig.11 Structure diagram of typical channels

雷诺数计算公式为

(2)

式中，Re为雷诺数;ρ为流体密度;L为流场特征长度;μ为动力黏度。

以最典型的圆管形孔喉结构为例，孔道渗流量为q，则孔道雷诺数计算公式为

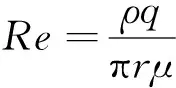
(3)

式中，r为圆管半径。

对于某一孔道，孔隙及喉道渗流量相等，喉道部位由于特征长度(喉道的孔径)小于孔隙，则其雷诺数大于孔隙，如此在多孔介质内部渗流时可能出现孔隙与喉道不同的渗流状态;另外，根据渗流过程观测可知，孔隙不同位置渗流活跃性差异较大，则不同区域也可能存在不同的渗流状态，如此造就本试验模型渗流试验为层流+紊流的混合流形式。

4 结论与展望

(1)基于真实砂层试样CT图片构建的二维孔隙模型，采用高精度光固化型3D打印机，制备了透明状二维微细孔隙试验模型，构建了渗流试验系统，开展了12个注水流量梯度、4个不同注水方向的渗流试验，实现了注水压力的高密度监测及孔隙渗流过程的可视化观测。

(2)二维孔隙渗流过程观测发现，在渗流过程中分流及汇流持续发生，试验模型不同位置孔隙渗流的活跃性差异较大;随着水力梯度J的增大，采用达西定律计算的渗透系数k整体呈现减低趋势，两者关系可用幂函数拟合，且J越大相关性越强。

(3)渗流速度v与水力梯度J呈高度相关的二次函数关系，符合Forchheimer非线性渗流公式，同模型90°改变注入方向时，同等v条件下，J差异较大，表现为明显的各向异性特征;多孔介质渗流为“层流+紊流”的混合流，随着v的增加，紊流惯性力对J的占比逐渐提高，其主要与孔隙介质中孔隙及喉道结构特征有关。

本次模型构建先试用了几个砂岩试样，但模型孔隙的连通极差，故改为松散砂层进行，后续可尝试采用连通性好的砂岩试样开展类似试验研究;常规多孔介质非线性渗流研究常分段进行，力求精确划分层流、紊流，但界限一直较为模糊[23-28]，此次研究尝试从微观角度探索了孔隙介质层流、紊流并存的机理，但相关研究成果还需进一步验证。