煤层覆岩采动裂隙应力-渗流耦合模型及涌水量预测

程香港，乔 伟，李 路，江传文，倪 磊

(1.中国矿业大学 资源与地球科学学院，江苏 徐州 221000; 2.上海勘测设计研究院有限公司，上海 200434; 3.安徽省水利水电勘测设计院研究总院有限公司，安徽 合肥 230088)

煤炭是我国主要能源之一，煤炭资源的开采关系到国民经济的发展，矿井突水水害严重制约着我国煤炭安全高效生产[1]。据不完全统计，自2000年至今，煤矿突水事故频发，突水事故高达814起，死亡人数高达4 000多人，经济损失高达到400多亿人民币[2]。煤矿突水不仅严重影响了矿井井巷开拓和回采工作，造成重大的人身伤亡和经济损失，而且还对矿区水资源与环境造成巨大的破坏。矿井涌水量的预测是煤矿安全生产、防排水设计的重要依据，因此，矿井涌水量的预测工作极为重要。

目前，我国在煤炭开采过程中形成了大量矿井涌水量预测方法，如解析法、水文地质比拟法、统计学法、数值法等[3]。杜敏铭等[4]概述了工程中常用的矿井涌水量预测方法，分析各方法的主要特点及适用性，提出了对矿井涌水量预测方法的展望。刘基等[5]运用Visual Modflow软件构建葫芦素煤矿地下水流数值模型，研究了矿井涌水量随采掘进度的动态变化规律及回采期间矿井涌水量。黄欢[6]综述了矿井涌水量的预测方法，并提出了矿井涌水量预测发展趋势，许多学者认为结合数值模拟的耦合模型成为预测矿井涌水量的主要发展趋势。因此，深入研究应力-渗透耦合作用对矿井涌水量的预测有着重要的意义。

国内外学者对应力-渗流耦合已经做了很多研究工作，BATCHELOR[7]从理论上推导出了牛顿流体在平行板裂缝中的运动公式，实现了单裂隙应力-渗流耦合。张玉卓[8]、张金才等[9]基于孔隙弹性力学理论及修正的立方定律模型，推导出应力与渗透率的方程，通过有限元软件耦合应力与渗流的联系，研究了裂隙岩体的应力变化与渗透性变化的关系特征。白国良等[10]基于立方定律，推导了以应变为参数的采动岩体等效渗透系数，利用FLAC3D软件建立了采动岩体等效连续介质流固耦合模型，研究了采动岩体的渗流特征及普遍规律。孟召平等[11-12]通过室内试验研究了不同岩石应力应变与渗透率的关系，建立采后应力与渗透率的三维定量计算模型，研究了岩体应力、渗透系数的动态变化规律。朱红光等[13]讨论了立方定律的前提条件并指出立方定律的局限性，提出了一个粗糙岩体裂隙的离散等效几何模型，为实际岩体裂隙中渗流行为的分析提供了新的手段。王志良等[14]基于格子Boltzmann方法，考虑了裂隙面粗糙度的因素，提出了立方定律在粗糙裂隙面渗流的修正公式，为研究复杂粗糙裂隙的水力特征奠定了一定的基础。以往的矿井涌水量预测方法常用传统的井流公式，由于勘探阶段获取的水文地质参数为钻孔数据，数据较为离散，而且分布不均匀，未考虑采动引起的覆岩裂隙渗透特性变化，预测结果与矿井实测涌水量相比误差较大，精度较低。

笔者以陕西金源招贤煤矿首采区1307工作面为例，基于导水裂隙带发育和正交实验设计基本原理，建立修正后的采动裂隙应力-渗透耦合计算模型，研究了1307工作面采动渗透系数的动态变化规律并进行矿井涌水量的预计。结合实测涌水量，与不同的试验模型预计的涌水量进行对比，探讨出一种相对符合实际的间距及隙宽组合形式下试验模型，提出了一种矿井涌水量预测新思路，为顶板水害防治提供了依据。

1 地质及开采概况

招贤煤矿一采区位于陕西省麟游县招贤镇，1307工作面为一采区的首采工作面，位于招贤煤矿一采区东南翼，地面主要以丘陵和山地为主。1307工作面的含煤地层为侏罗系中统延安组，3号煤层厚度为2.45～28.67 m，均厚14.77 m，均采厚9.9 m，工作面起止标高+760～+879 m，工作面走向为1 144 m，宽160 m。采用走向长壁采煤法综放开采。顶板为深灰色泥岩、砂质泥岩、粉细砂岩与灰白色中粗粒砂岩互层。研究区内分布有麦里沟向斜和四郎沟向斜，两向斜轴向西南，北翼倾角较陡，南翼倾角较缓，煤层平均倾角约为6°，采区内无煤层露头。煤层上覆岩层为中硬类岩层，其直接充水含水层为直罗组砂岩裂隙含水层和延安组煤层及顶板砂岩含水层。研究区内地层由老至新依次有:侏罗系下统富县组(J1f)、中统延安组(J2y)、直罗组(J2z)、安定组(J2a)，白垩系下统宜君组(K1y)、洛河组(K1l)，新近系(N)及第四系中—上更新统(Q2+3)、全新统(Q4)，1307工作面地质剖面图如图1所示。

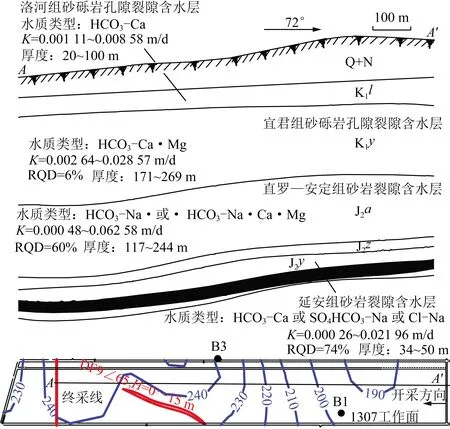
图1 1307工作面地质剖面Fig.1 Geological section of 1307 working face

1307工作面水文地质参数见表1，宜君组含水层钻孔单位涌水量为0.006 1～0.037 7 L/(s·m)，属中等富水，但由于宜君组厚度为171～269 m，相对较厚，具有较大的顶板水害威胁，因此，判定其富水性为强富水。

表1 1307工作面水文地质参数Table 1 Hydrogeological parameters of 1307 working face

2 采动裂隙渗流与应力耦合分析

国内外许多学者研究表明，覆岩采动裂隙随着工作面的推进而发生改变，顶板覆岩存在着3个不同的区域:垮落带、裂隙带和弯曲下沉带[15]。

如图2所示，在工作面直接顶的塌陷区域，上覆岩体直接垮落至工作面，呈现出大小不同的不规则块体。每个破碎岩层中的相邻块体在裂隙带中完全或部分接触，从裂隙带的下部向上，垂向的裂隙数量逐渐减少，裂隙间间距增大，隙宽逐渐减小。在裂隙带的上部是弯曲下沉带，没有形成贯穿岩层的垂向裂隙。裂隙带范围内的天然岩体受采动扰动影响后，形成大量的裂隙面，这些裂隙面切割了岩体，形成了采动裂隙网络。

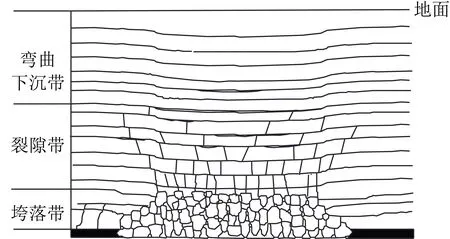
图2 煤层开采过层中覆岩运动区域Fig.2 Area of overlying strata movement in coal seam mining

在采动裂隙网络中，采动裂隙分布杂乱，形态各异。但是，岩体采动裂隙中垂向裂隙与横向裂隙相对较为发育，其中垂向或者近垂直的裂隙主要为采动岩层破断所形成，而横向裂隙大多为岩层层面裂隙，所以本文假设煤层开采上覆岩层的采动裂隙是具有三向相互垂直裂隙的正交裂隙网络，如图3所示。

图3 正交裂隙网络Fig.3 Orthogonal fracture network

由于采动裂隙导通含水层中的地下水均向采空区运移，z方向上裂隙渗流变化的特征对涌水量的预测具有现实意义，因而，笔者基于建立的正交裂隙网络，结合公式，推导了z方向上采动裂隙渗透系数，用于矿井涌水量的计算。

综上所述，笔者研究了煤层覆岩采动粗糙裂隙面下应力-渗流耦合特征，并探寻矿井涌水量预测更为精细的方法，研究工作具体流程如图4所示。

图4 流程Fig.4 Flow chart

煤层的开采伴随着覆岩运动的产生，导致采动裂隙渗流网络与岩土体应力场发生改变，水体渗流运动与岩体应力场相互作用。裂隙中渗流水运动遵循N-S方程，对于理想光滑平面板裂隙渗流，BATCHELOR[7]从理论上推导出了立方定律:

(1)

式中，q为裂隙水流的单宽流量;g为重力加速度;b为裂隙隙宽;μ为水的黏滞系数;J为水力梯度。

由于在实际工程地质条件中，天然裂隙面均为粗糙的，一些学者基于裂隙面的粗糙程度对立方定律进行了修正。AMADEI等[16]以非经验的方法深入研究了裂隙面粗糙度对立方定律的影响，将解析解和数值模拟相结合，得到了经验公式:

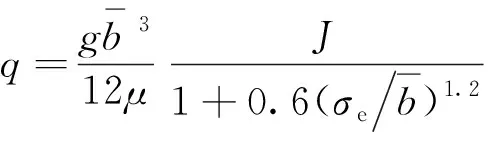
(2)

王志良等[14]在此基础上对式(2)进行修正，得到层流状态下粗糙裂隙面立方定律修正公式为

(3)

由式(3)，根据Darcy定律可知

(4)

则在初始应力场条件下，层流状态下的裂隙水在粗糙裂隙面中渗透系数为

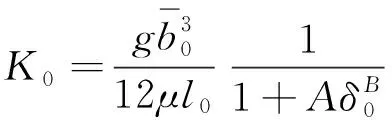
(5)

孔径的变化影响渗透率的变化，孟召平等[11]在前人研究基础上推导出两组相互正交的裂隙渗流与隙宽变化方程，其方程可表示为

(6)

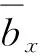
根据广义胡克定律，如式(7)所示，迭代可得式(8):

(7)

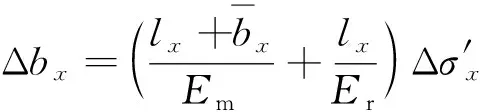
(8)

同式(7)，(8)，则Δby可表示为

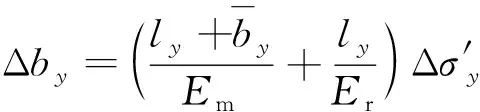
(9)

式中，Δutx为x方向上岩体变形总量;Δbrx为x方向上岩块变形总量;Δεtx为x方向上岩体应变;Δεrx为x方向上岩块应变;Δσ′x为x方向上应力增量;Δσx为x方向上应力变化量;Δσy为y方向上应力变化量;Δσz为z方向上应力变化量;ν为泊松比;Em为岩体杨氏模量;Er为岩块杨氏模量。

由于岩体与岩块的杨氏模量有

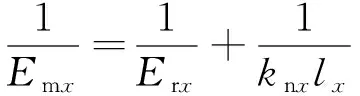
(10)

将式(8)～(10)代入式(6)中，可得

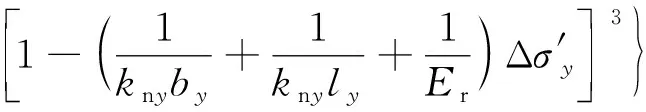
(11)

将式(5)代入式(11)中，可得修正后的三维裂隙应力-渗流网络计算模型:

(12)

同式(12)，Kx，Ky可表示为

(13)

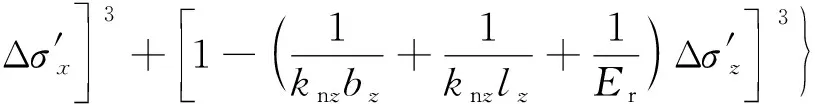
(14)

式中，knx,kny,knz分别为在x,y,z方向断裂的法向刚度；Kx为x方向上渗透系数;Ky为y方向上渗透系数。

3 采场覆岩变形破坏渗透性

岩体渗透系数的变化受相对粗糙度、隙宽、间距以及采动岩体应力增量的影响，由于在实际工程中相对粗糙度、隙宽、间距以及采动岩体应力增量测量较为困难，因而，笔者使用FLAC3D软件模拟计算了采动岩体的应力增量，并结合实际工程情况，假设与讨论了各影响因素的取值，代入式(11)，(12)进行分析采场覆岩变形破坏渗透特征。

3.1 数值模拟模型

根据招贤煤矿1307工作面实际地质条件，建立如图5所示的有限元三维数值模型，模型长、宽、高为1 250 m×560 m×552 m，根据实际工程地质条件，考虑到边界条件的影响，结合矿山开采沉陷理论，设置煤层开挖高度为10 m，两侧留设足够的煤柱来确保模型边界在采动影响之外，模型侧面设置限制水平移动，模型底面限制水平移动，模型顶部施加垂向荷载模拟上覆岩层的自重。

图5 数值模拟模型Fig.5 Numerical simulation model

模型上覆岩层岩性及煤的物理力学参数指标见表2。

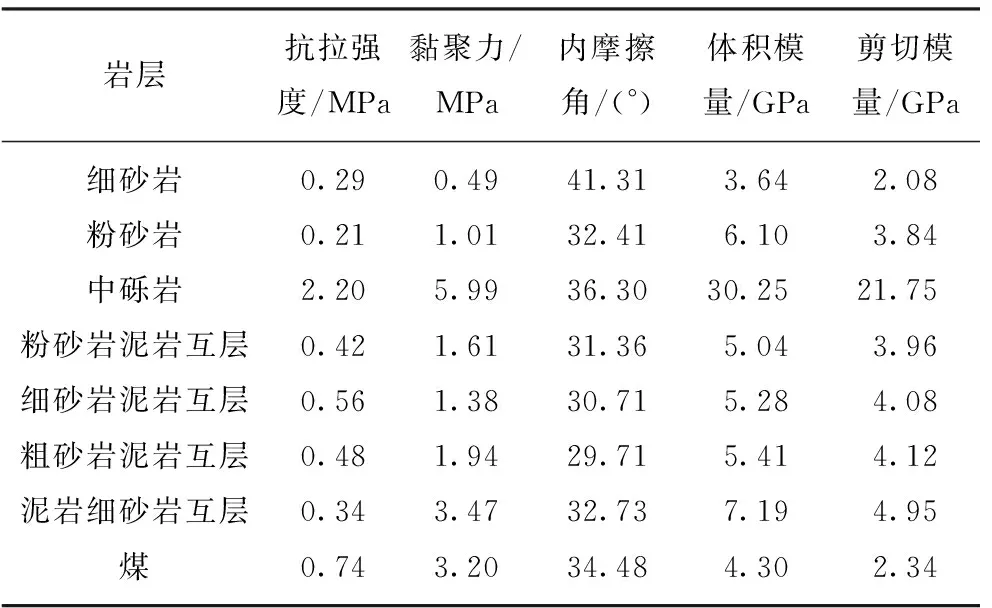
表2 上覆岩层岩性及煤的物理力学参数指标Table 2 Overburden rock lithology and physical and mechanical parameters of coal

3.2 覆岩“两带”高度

煤层开采后，上覆岩层形成的垮落带和裂隙带会随着煤层开采推进长度的增加发育到最大值，而后趋于稳定。工作面采动塑性区如图6所示，结果表明:采空区上方中部岩层主要为拉张破坏区，而在开切眼及煤壁前方出现剪应力区。图6中塑性区的范围表明此处岩层已发生破坏，靠近采空区以拉张破坏为主的区域可视为垮落带，覆岩弹性区和剪切破坏区的上限可视为导水裂隙带的上限，由此得到导水裂隙带发育的最大高度，测量可知此时导水裂隙带的发育高度。

数值模拟分析表明:工作面开采700 m时,如图6(b)所示，覆岩塑性区在纵向上高度发育至最大值，止于煤层顶板以上197.7 m，最终确定数值模拟裂隙带发育最大高度为197.7 m。

为了清晰的观测煤层开采过程中，上覆岩层“两带”高度发育情况，根据上覆岩层地质条件，结合相似模拟试验台5 m×0.3 m×2.5 m(长×宽×高)，设计了工作面相似模拟试验，煤层开采高度为10 m，相似比为1∶300，相似模拟模型如图7所示。

图7 相似模拟模型示意Fig.7 Schematic diagram of similar simulation model

结合相似模拟实验对裂隙带高度的研究结果，得到采动对裂隙带发育高度等影响及趋势，如表3和图8所示。

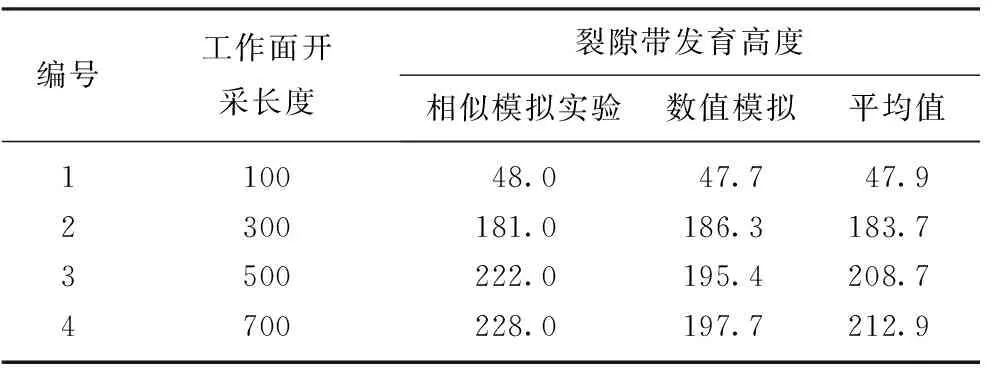
表3 采动不同长度的裂隙带发育高度值Table 3 Development height values of crack zones with different lengths m

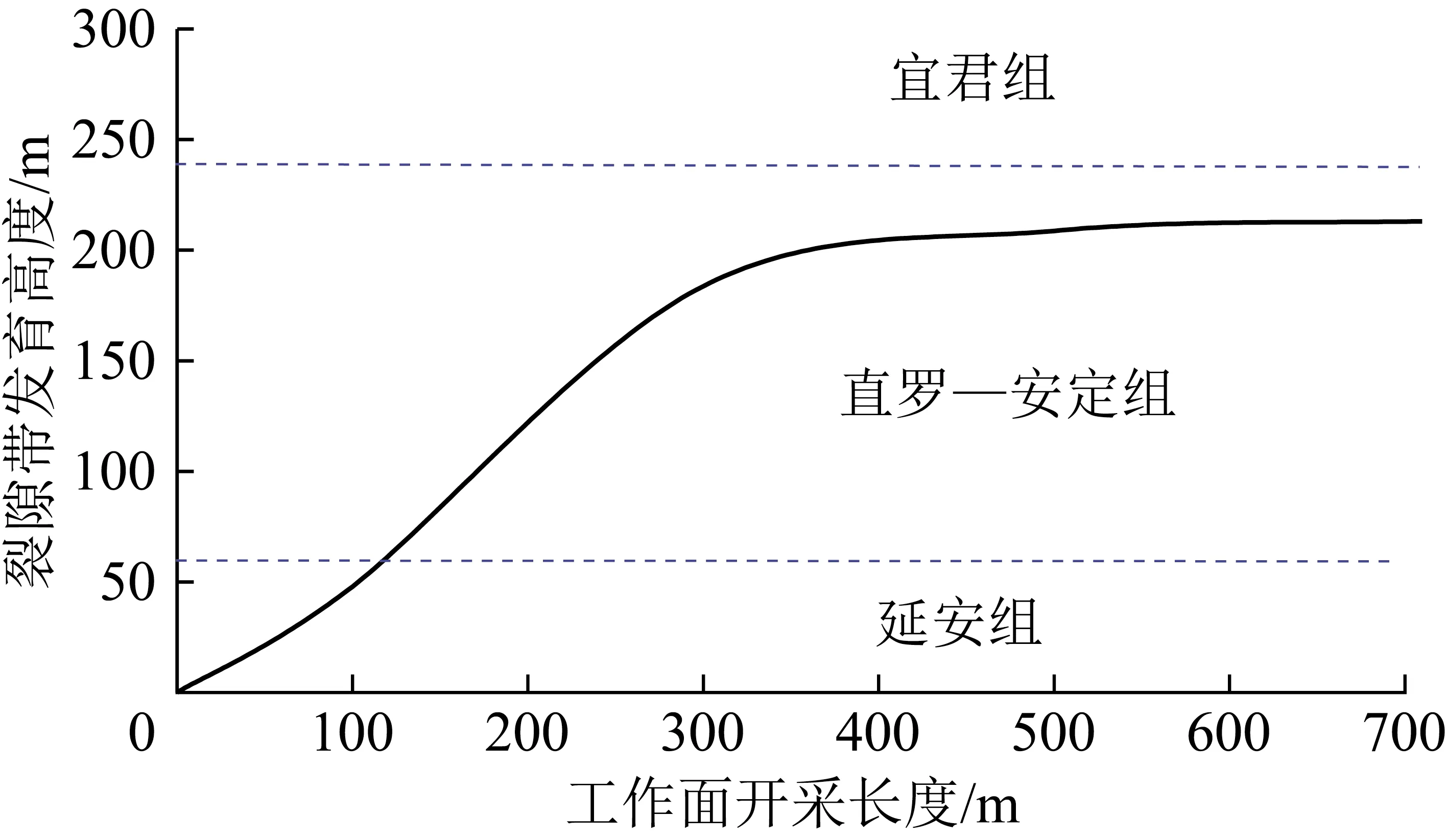
图8 工作面采动裂隙带发育趋势Fig.8 Development trend of mining fracture zone

根据《煤矿防治水手册》中垮落带和导水裂隙带高度经验公式，结合现场实测数据、数值模拟结果以及相似模拟实验结果，得到采动垮落带和导水裂隙带发育最大高度值，见表4。

表4 采动垮落带和导水裂隙带发育最大高度平均值Table 4 Maximum height average of the development of the caving zone and the water guiding fracture zone m

3.3 裂隙正交网络模型建立及讨论

由于工作面推进至一定长度后，导水裂隙带发育高度不再发生改变,笔者根据表4采动垮落带和导水裂隙带发育最大高度的平均值将工作面覆岩进行分层计算，依此用于计算分层区域的垂直渗透率的变化比值，分层如下:层位I,从距顶板0 m开始至50 m;层位Ⅱ,从距顶板50 m开始至125 m;层位Ⅲ,从距顶板125 m开始至195 m。

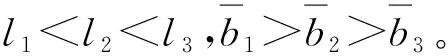
根据开采过程中矿压实时数据，小周期来压步距为10～20 m，初次来压步距为30～50 m，大周期来压步距为150～200 m，分析选取间距变量l以及隙宽b变量。假设层位I间距变量l1为10,15,20 m;层位Ⅱ间距变量l2为30,40,50 m;层位Ⅲ间距变量l3为150,175,200 m。隙宽b变量为0.05,0.01,0.005,0.001 m。

基于正交实验设计基本原理，笔者设计9种不同组合形式下的间距l及隙宽b试验模型，见表5，对不同试验模型下渗透率的变化进行探讨。

表5 裂隙正交网络模型Table 5 Fracture orthogonal network model m

3.4 采动应力场变化分析

采用FLAC3D数值模拟软件对覆岩采动岩体变形破坏的应力场进行数值模拟，选择y=280 m的垂直横截面用于分析结果，开采100，700 m时围岩应力场分布如图9所示。

图9 工作面开采100,700 m时围岩的应力场分布(单位:MPa)Fig.9 Stress field distribution of surrounding rock when mining face is 100,700 m (unit:MPa)

煤层的开采产生扰动，导致上覆岩层应力场发生变化。随着采动长度的增加，应力场扰动范围增大，应力变化速度逐渐降低。采空区两侧及直接顶范围内，应力变化大。采空区四周应力较为集中，采空区中间范围内应力较为松弛。

如图9(a)，(b)所示，x方向应力场应力分布集中区域在采空区的两侧，在采空区的上方的岩层受到挤压作用影响，出现“O”型闭合的应力集中区。随着采动距离的增加，采空区的两侧由于受到拉伸作用的影响，应力有所减小，而“O”型闭合应力区向上传递;如图9(c),(d)所示，y方向应力场分布相对平缓，应力集中区与x方向应力场分布相同，采空区直接顶为应力松弛区且随着距采空区距离增大应力逐渐恢复至初始应力水平，在其上方出现“O”型闭合的应力集中区。随着采动距离的增加，采空区的两侧应力变化相对较缓，“O”型闭合应力区向上移动。如图9(e),(f)所示，z方向应力场分布较为简单，采空区两侧为应力集中区，采空区上方为应力降低区且随着距采空区距离增大应力逐渐恢复至初始应力水平。

3.5 渗透率变化分析

根据上述裂隙正交网络模型，笔者简化渗透系数的计算，假设岩石是均匀的各向同性的，即岩体的破裂参数在x,y和z方向上是一样的，δ1=0.018 45，δ2=0.016 74，δ3=0.013 08，Er=21 GPa，knx=1 GPa/m，ν=0.23，μ=0.981，A=46.946，B=1.230 5。结合数值模拟工作面开采700 m时得到的应力增量(Δσx，Δσy和Δσz)代入式(11),(12)，计算出煤层覆岩渗透系数及变化比值。

根据9组模型模拟垂向渗透性的变化，选取模型3垂向渗透系数的变化比值,结果如图10所示。

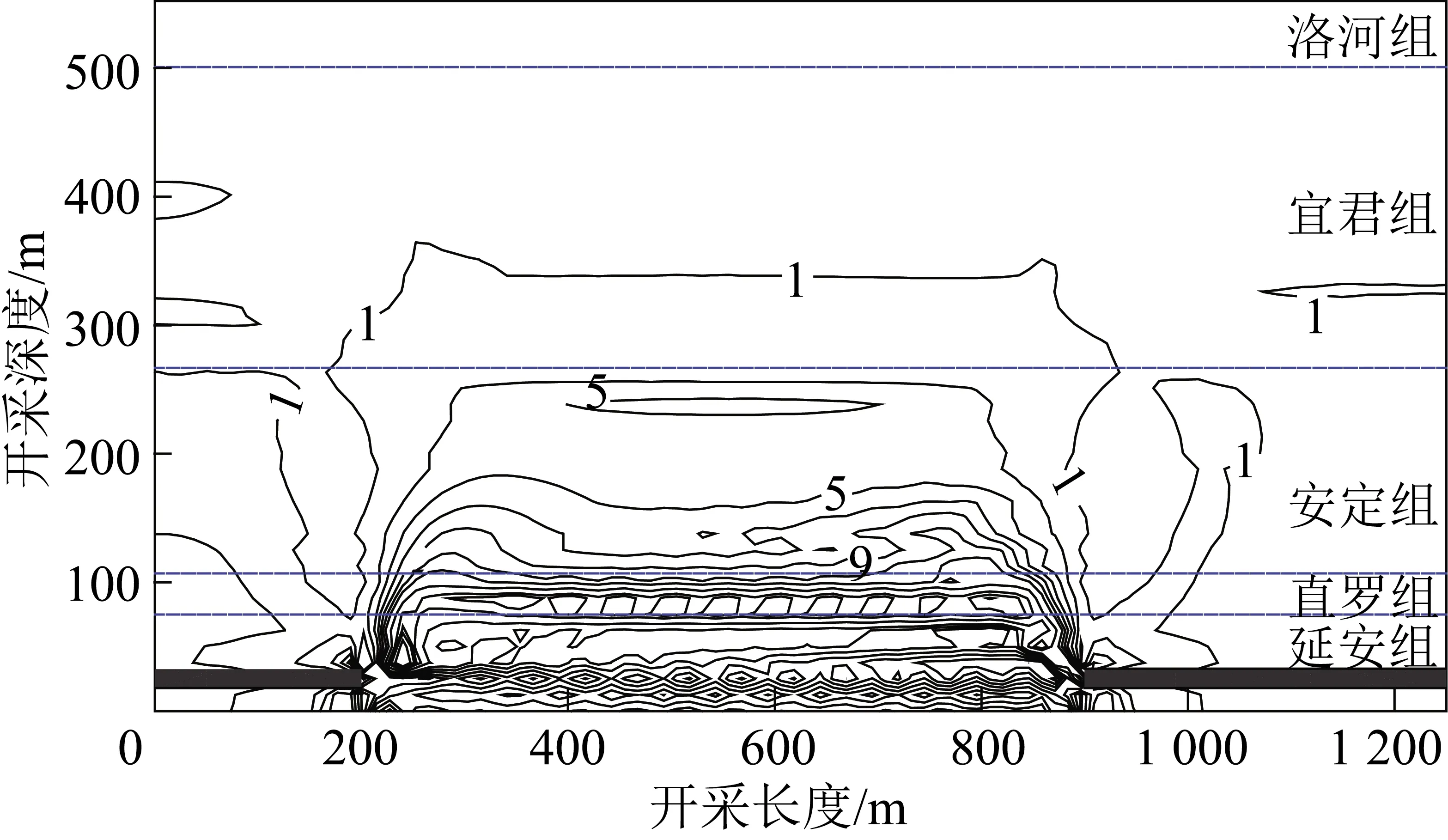
图10 工作面开采700 m时垂向渗透系数的变化比值(Kz/Kz0)Fig.10 Ratio of change in vertical permeability coefficient when working face is mined at 700 m(Kz/Kz0)

由于采动引起覆岩移动、变形以及岩层裂隙形成，导致上覆岩层渗透率发生了改变。由图10可以看出，部分岩层受到采动的影响，导致渗透系数增加;存在部分岩层受到压实作用的影响，导致渗透系数降低。岩层距离采掘工程越近，受到扰动越大，渗透系数改变越剧烈。岩层距离采掘工程越远，扰动影响越低，渗透系数变化越小。即:在垂向上，随着岩层距采空区的距离越大，渗透系数的变化比值越小。

此外，渗透性变化的区域在垂直切片上呈拱形，且区域的范围大于应力变化的范围。将工作面开采700 m时垂向渗透系数的变化按照研究区区域含水层层位进行划分，统计了9组模型各含水层层内垂向渗透系数变化，见表6。

表6 9组模型区域含水层垂向渗透系数变化统计Table 6 Statistical analysis of vertical permeability coeff-icient change of aquifers in 9 groups of model areas

由表6结果可知，延安组砂岩裂隙含水层垂向渗透系数变化范围在1～15倍，直罗—安定组砂岩裂隙含水层垂向渗透系数变化范围在1～12倍，宜君组砂砾岩孔隙裂隙含水层以及洛河组砂砾岩孔隙裂隙含水层垂向渗透系数变化较小，这是由于采动形成的导水裂隙带最大高度未至宜君组，宜君组与洛河组受到扰动小，渗透率变化小。延安组砂岩裂隙含水层及直罗—安定组砂岩裂隙含水层的渗透率变化对工作面矿井涌水量预计极其重要。

据此，统计9组模型在延安组砂岩裂隙含水层及直罗—安定组砂岩裂隙含水层垂向渗透系数平均值，见表7。

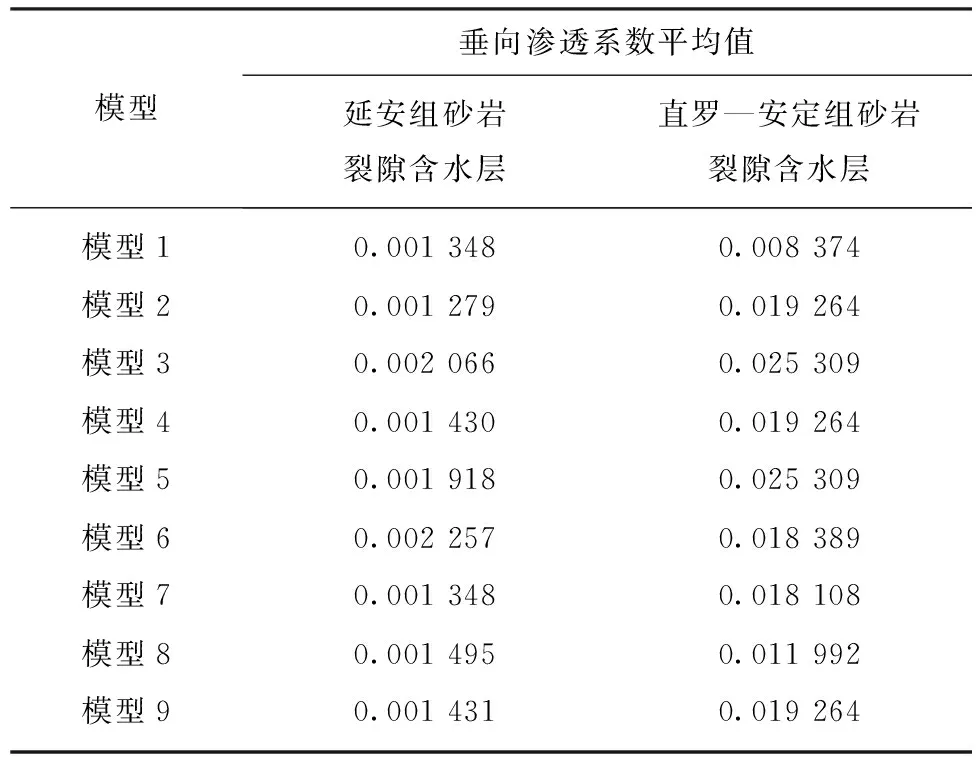
表7 9组模型垂向渗透系数平均值统计Table 7 9 sets of models vertical permeability average statistics m/d

4 涌水量预计

招贤煤矿1307工作面开采3煤，根据图6可知，导水裂隙带未波及至宜君组砂砾岩孔隙裂隙含水层，因此预计工作面涌水量主要考虑延安组、直罗组—安定组含水层。含水层厚度采用各水文孔揭露的含水层厚度平均值;初始渗透系数采用相应含水层段的渗透系数加权平均值;水位降深为各水文孔相应含水层水柱高度的平均值，所选择的水文地质参数详见表8。

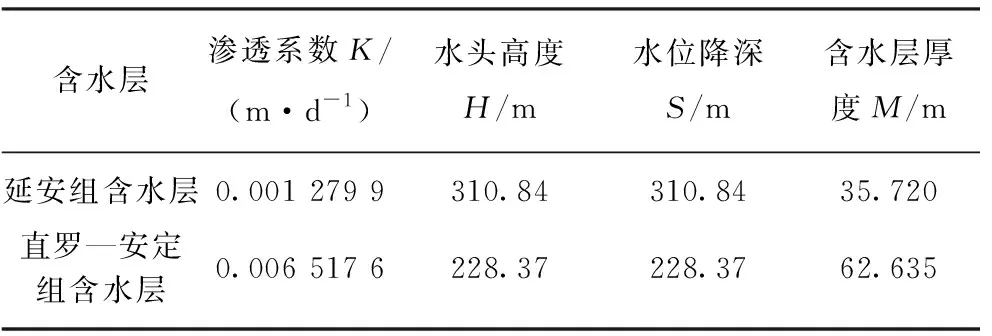
表8 水文地质参数平均值Table 8 Hydrogeological parameters average list

4.1 计算公式选取

由于9组模型计算得到的垂向渗透系数为区域平均值，因此，采用集水廊道法较为合理。根据1307工作面水文地质特征及采区工程地质概况，采用水平集水廊道法计算工作面涌水量[17]，有

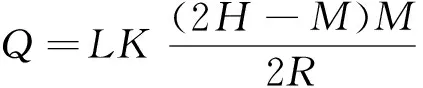
(15)

式中，Q为矿井涌水量，m3/d;L为集水廊道法边帮总长，m;H为水头高度，m;R为影响半径，m;M为含水层厚度，m。

4.2 工作面顶板导水裂隙带发育分段

根据图8导水裂隙带发育趋势，结合研究区工程地质概况，将1307工作面顶板充水含水层划分成3个不同涌水区段，分别为区段I,Ⅱ,Ⅲ，如图11所示。

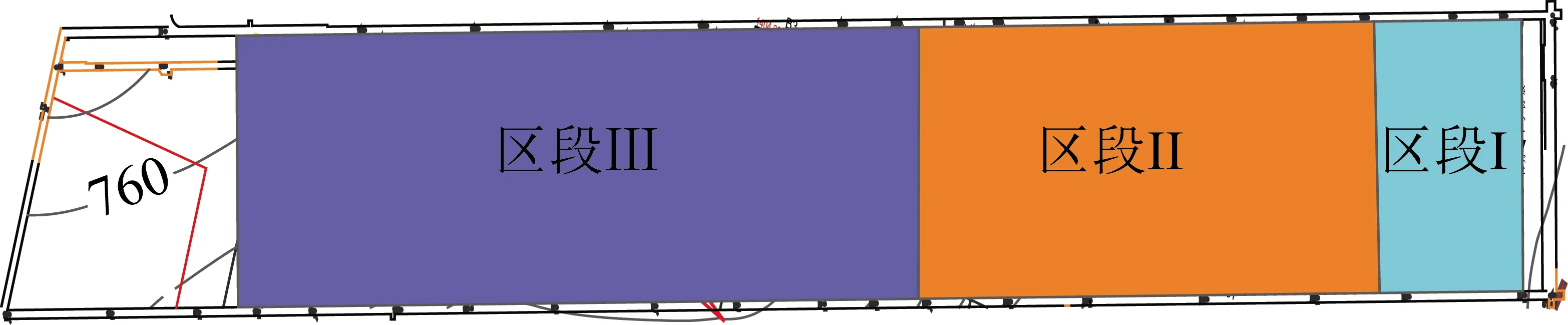
图11 1307工作面顶板充水含水层分段Fig.11 1307 working face top water-filled aquifer segmentation

(1)区段I。从开切眼开始至120 m处，导水裂隙带发育至延安组顶部，即将突破延安组砂岩裂隙含水层。

(2)区段Ⅱ。距开切眼120～500 m，该段工作面推进至500 m左右时，导水裂隙带高度发育缓慢。此时，导水裂隙带发育高度突破延安组煤层顶板砂岩含水层，但尚未突破至宜君组砾岩孔隙裂隙含水层。

(3)区段Ⅲ。距开切眼500 m至终采线，导水裂隙带高度发育稳定。此时，导水裂隙带发育高度未突破至宜君组砾岩孔隙裂隙含水层。

4.3 预测结果及分析

工作面开采时，集水廊道法预测工作面涌水量区段I为采空区4侧补给，区段Ⅱ与区段Ⅲ为3侧补给，工作面总涌水量为各区段之和，根据表7各模型的渗透率平均值，通过计算，矿井涌水量预测结果见表9，预测涌水量与实测对比，如图12所示。

表9 涌水量预测结果Table 9 Result of water inflow prediction m3/d

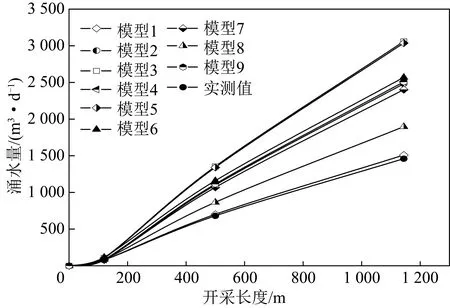
图12 预测涌水量与实测对比Fig.12 Comparison of predicted water inflow and measured water inflow

由表9可知，采用集水廊道法计算得到1307工作面回采至120 m时涌水量为77.55～115.07 m3/d;回采至500 m时涌水量为700.87～1 353.68 m3/d;回采至终采线时涌水量为1 508.93～3 058.99 m3/d，模型1矿井涌水量预测结果最小，模型3矿井涌水量预测结果最大，模型2、模型4、模型6、模型7与模型9矿井涌水量预测结果较为接近。

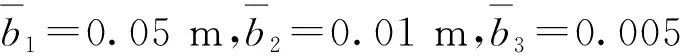
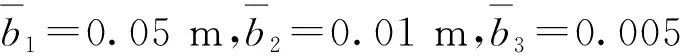
在离散元软件中建立裂隙渗流模型如图13所示。在数值模型的顶部和底部分别设置了水压3 MPa和0，四周设置为不透水边界，假定流体不可压缩，且渗流方向仅在z方向上，将渗流模型分层且按照模型一的间距组合及隙宽组合进行设置，当渗流稳定时，截取模型切片上渗流速度进行分析，如图14所示。

图13 裂隙渗流模型Fig.13 Fracture seepage model

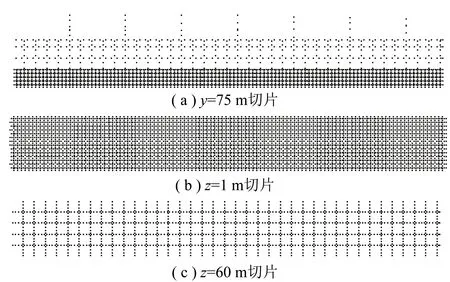
图14 模型裂隙渗流速率结果切片Fig.14 Slice plot of model seepage rate results

由图14可知，上覆岩层从上到下，随着岩体破碎程度的增加，渗流路径密度越高，渗流速率逐渐降低，这是由于层位高、水压大、过水断面小所导致的。当渗流稳定时，z=1 m切片上平均裂隙渗流速率为0.001 327 5 m/d，z=60 m切片上平均裂隙渗流速率为0.012 168 m/d，与裂隙应力-渗流耦合模型计算的结果基本相符，说明了裂隙应力-渗流耦合模型是较为可靠的。

5 结 论

(1)结合上覆岩层采动变化特征，建立了覆岩裂隙网络，基于煤层覆岩采动裂隙面的粗糙程度，对裂隙应力-渗流耦合计算模型进行了修正，提出了修正后的三维裂隙应力-渗流网络计算模型。

(2)对于煤层覆岩采动应力-渗流变化特征，通过模型分析，得到随着采动推进长度的增加，采空区四周应力分布集中，顶部范围内应力分布相对松散，应力场和渗流场的扰动范围增大，且渗流场扰动范围大于应力场扰动范围。此外，渗透系数的变化在不同方向上具有一定的差异，渗透系数在水平方向上的影响范围明显小于在垂向上的影响范围，但在水平方向上的变化要大于垂直方向上的变化。

(3)基于导水裂隙带发育规律和正交试验设计原理，设计了9种不同间距及隙宽组合形式下试验模型，通过修正后的裂隙应力-渗流网络计算模型，分析了覆岩采动渗透率变化规律。分析结果表明，受采动的影响，上覆岩层渗透率发生了改变。在垂向上，岩层距离采掘工程越近，受到扰动越大，渗透率改变最为剧烈。岩层距离采掘工程越远，扰动影响越低，渗透率变化越小。

(4)依据顶板导水裂隙带发育对工作面分段，结合9种试验模型的采动渗透系数计算结果，采用集水廊道法对矿井涌水量进行了预计，并与已有实测数据进行了对比。通过对比表明，模型1的矿井涌水量预测结果与实测基本相符，说明模型1间距及隙宽的组合形式相对较为符合研究区实际工程情况，对指导下一工作面及相似矿井涌水量具有一定的指导意义。

(5)基于离散元软件裂隙渗流模型，结合模型1组合形式，对裂隙应力-渗流耦合计算模型的可靠性进行探讨，结果表明，离散元软件裂隙渗流模拟结果与裂隙应力-渗流耦合模型计算的结果基本相符，说明裂隙应力-渗流耦合模型是较为可靠的。