低温环境下红砂岩蠕变特性及其模型
2020-09-16宋勇军张磊涛任建喜陈佳星车永新杨慧敏
宋勇军,张磊涛,任建喜,陈佳星,车永新,杨慧敏,毕 冉
(西安科技大学 建筑与土木工程学院,陕西 西安 710054)
流变性是岩石的重要力学特性之一,与岩体工程的长期稳定性紧密相关。许多大型岩体工程,如寒区隧道、西部地区煤炭矿井建设及近年来备受关注的液化天然气地下低温储存等,都不同程度地涉及低温环境下岩石的长期力学行为,其中西部地区煤炭资源大多上覆较厚的富水白垩系软岩地层,矿井建设多采用冻结法施工。这就需要研究岩石在长时间低温作用下的力学响应与变形机制。
近年来,众多学者在低温岩石的力学特性和损伤破坏研究方面,取得了较为丰硕的成果。INADA Y和YOKOTA K[1]对饱水与干燥状态下的花岗岩和安山岩进行了不同温度条件下的单轴压缩和拉伸试验,研究了岩石力学性质随温度的变化规律;AOKI K等[2]对不同温度条件下的花岗岩、流纹岩等岩石进行了单轴压缩和巴西劈裂试验,研究了不同温度条件对岩石强度、弹性模量等力学参数的影响规律;MATSUOKA[3]对不同类型的岩石进行了多次冻融循环试验,研究了毛细吸力及孔隙内冻结冰对岩石冻融破坏规律的影响;YAMABE T和NEAUPANEK K M[4]进行了岩石冻融循环热膨胀应变测试试验,发现抗压强度和弹性模量随温度的下降而增大,试样强度随冻融循环次数增加而降低,抗拉强度降低比抗压强度明显;CHEN T C等[5]对凝灰岩进行冻融循环试验,研究了不同含水率对冻融后岩石强度的影响规律;PARK C等[6]研究了-160~-40 ℃温度条件下,岩石导热系数、比热等参数随温度而变化的规律;徐光苗等[7]对干燥与饱和状态下的砂岩和页岩进行不同温度条件下的单、三轴压缩试验,研究了温度(-20~20 ℃)对岩石单轴抗压强度、弹性模量等力学参数的影响规律;唐明明等[8]对低温条件下的花岗岩进行了单轴和三轴压缩试验,发现岩石强度随着温度的降低而提高,但存在一个强度趋于稳定的温度界限值,其值约为-40 ℃;YAVUZ[9]对安山岩进行了冻融循环试验,结果表明岩样的抗压强度和纵波波速均降低,但吸水率和孔隙率增大;奚家米等[10]对饱水砂质泥岩开展不同围压及不同温度(20~-30 ℃)状态下的单轴及三轴压缩试验,研究了低温对砂质泥岩力学性质的影响规律;李栋伟等[11]对白垩系冻结软岩进行了三轴蠕变试验,引入MISES及Mohr-Coulomb强度准则建立软岩蠕变模型;单仁亮等[12-13]对-10 ℃下的冻结红砂岩进行不同应力水平的三轴蠕变试验,分析了应力水平、节理倾角对红砂岩蠕变特性的影响规律,并建立了适于冻结红砂岩蠕变特性的理论模型。
综上所述,低温条件下的岩石力学特性研究已有较为丰富的成果,但主要集中在瞬时力学特性及冻融损伤方面,对于低温作用下岩石蠕变特性及蠕变模型的研究还很少。基于此,笔者以陕西某煤矿立井冻结法施工中的红砂岩为研究对象,开展低温不同冻结温度的单轴加卸载蠕变试验,分析不同温度条件下的红砂岩黏弹塑性变形特性,并根据试验结果,引入分数阶微积分,建立考虑温度影响的非线性黏弹塑性模型,为低温条件下的岩体工程长期稳定性分析提供理论依据。
1 试样制备及试验过程
1.1 试样制备
试验选取陕西红砂岩作为研究对象,从现场取回大块红砂岩,采用钻孔取样法,加工成D×H=50 mm×100 mm(D为岩样直径,H为高度)的标准岩样,如图1所示。

图1 红砂岩岩样Fig.1 Rock specimens of red sandstone
试验前先将视觉上差别较大的岩样剔除,然后将选好的岩样放入烘箱中,在105 ℃温度下烘48 h至恒重,待其冷却至室温后取出,进行干密度和纵波波速测量。为减小岩样物理力学性质上的离散性对试验结果的影响,取干密度及波速相近的岩样进行试验。将选好的岩样在水中浸泡48 h后,测量岩样质量,得到岩样饱和含水率及孔隙度。红砂岩物理力学参数平均值见表1。

表1 红砂岩物理力学参数平均值Table 1 Average physical and mechanical parameters of red sandstone
1.2 试验设备及试验方法
低温岩石单轴加卸载蠕变试验在中科院冻土工程国家重点实验室MTS810岩石力学试验机上进行。试验机最大轴向荷载为250 kN,压力室温度控制误差为±0.5 ℃。低温岩石力学试验系统如图2所示。

图2 低温岩石试验系统Fig.2 Testing system for rocks under low temperatures
将制备好的饱和岩样,用乳胶套密封好,放入低温控温箱中恒温冻结24 h。同时,将 MTS 810岩石力学试验机上的压力室温度降至试验预设值。冻结完成后,将岩样放入试验机压力室中,继续恒温冻结2 h,以保证试验全过程岩样温度始终为试验设定温度。
为对比分析不同温度条件下的岩样在相同应力水平下的蠕变特性,根据岩样单轴抗压强度计算各级加载应力,采用多级加卸载方式进行蠕变试验。试验加载速率为0.01 MPa/s,每级荷载持续9 h后完全卸载至0 MPa,卸载速率为0.03 MPa/s,卸载后持续时间3 h。试验温度设置为20,-10及-20 ℃,每种温度取2个岩样进行平行试验,以取得各温度下单轴加卸载蠕变曲线的代表值。图3为单轴蠕变加卸载路径示意图。

图3 单轴蠕变多级加卸载路径Fig.3 Multi-level loading and unloading process in the uniaxial creep test
2 试验数据处理及结果分析
2.1 数据处理
ε=εm+εc
(1)

图4 典型加卸载流变曲线Fig.4 Representative rheological curve under loading and unloading
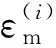
(2)
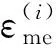

(3)

(4)

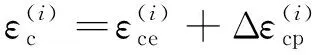
(5)
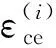
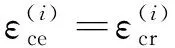
(6)

(7)
据此,在第n级应力水平σn作用下,其瞬塑性应变量和黏塑性应变量分别为
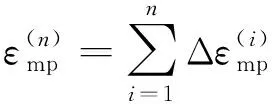
(8)

(9)
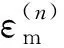

(10)

(11)
2.2 试验结果分析
图5为红砂岩试件在20,-10及-20 ℃时的单轴分级加卸载蠕变曲线。从蠕变曲线可以看出,低温对岩石变形有显著影响。随着温度的下降,同一应力水平下岩石的瞬时应变、蠕应变及岩石破坏时的应变都有所降低,而蠕变破坏强度有较大增长。
不同温度的岩样在蠕变破坏前各级应力水平下表现出衰减蠕变和稳定蠕变2个阶段,加速蠕变阶段则在最后一级应力水平下显示出来。另外,岩石衰减蠕变持续的时间较短,且随应力水平的增长呈增加趋势。从图5可以看出,温度对红砂岩的蠕变特性具有重要影响。随着温度的降低,岩样的瞬时变形和蠕变量大幅降低,如在第2级应力水平下,S4(20 ℃),S7(-10 ℃)及S9(-20 ℃)岩样的瞬时变形分别为7.074×10-3,4.960×10-3,1.650×10-3,降低幅度分别为29.88%和66.73%,蠕变量分别为2.02×10-3,4.74×10-4,4.30×10-4,降低幅度分别为76.53%和9.28%。同时,随温度的降低,蠕变破坏应力大幅增长,S4岩样在第3级应力水平下历经衰减蠕变、稳态蠕变和加速蠕变后破坏,蠕变破坏应力为6.6 MPa;S7岩样在第6级应力水平下破坏,蠕变破坏应力为12.7 MPa;S9岩样在第6级应力水平下,仅表现为衰减蠕变和稳态蠕变2个阶段,没有显示出加速蠕变及破坏的征兆。这是由于低温条件下饱和红砂岩内部孔隙水冻结成冰,使得岩石强度、弹性模量增大,岩石抵抗变形能力增强。因此,常温下红砂岩的蠕变表现为软岩蠕变,而低温下的红砂岩蠕变更接近于硬岩的蠕变曲线。
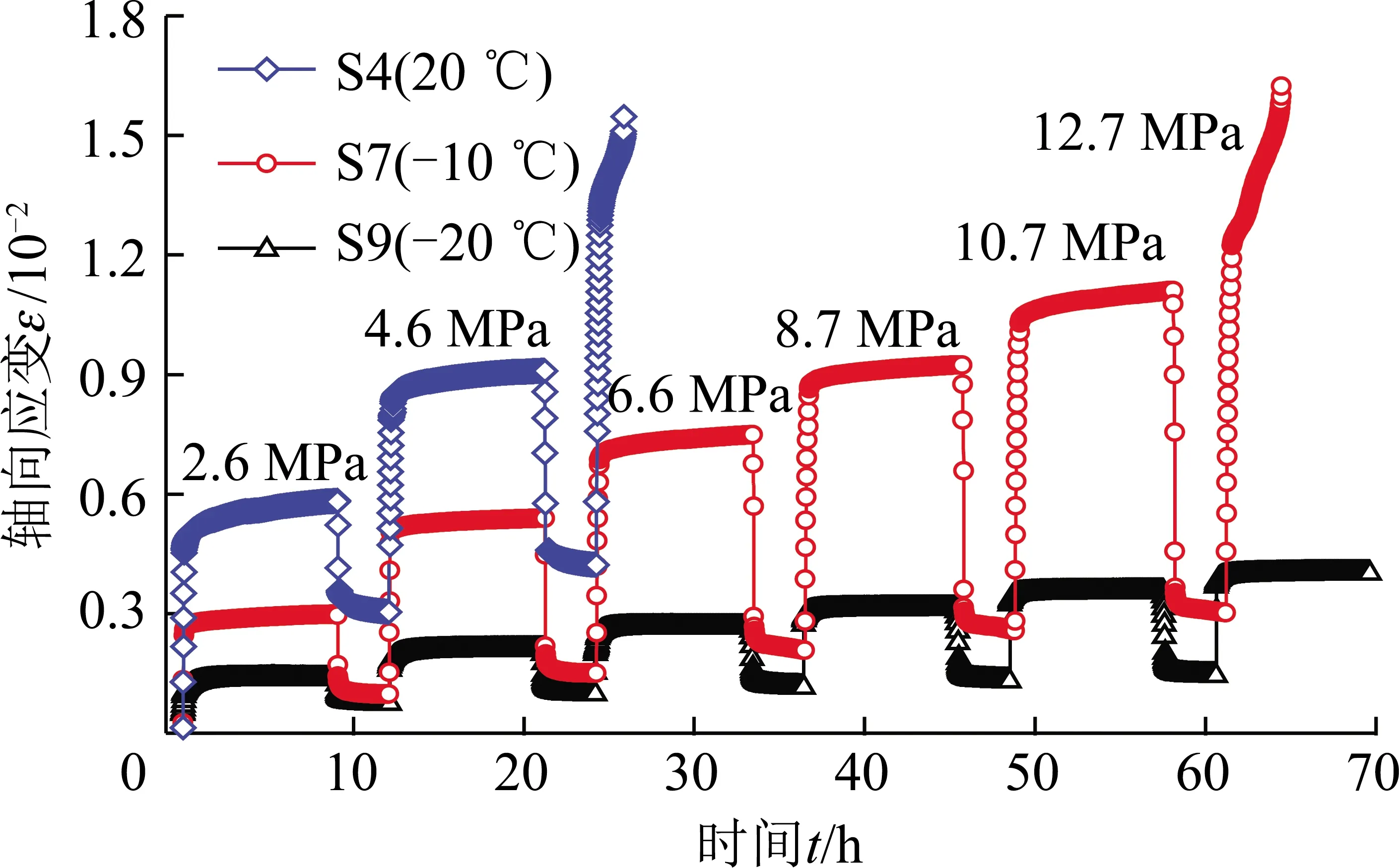
图5 不同温度下单轴蠕变加卸载曲线Fig.5 Uniaxial loading and unloading creep curves at different temperatures
2.2.1瞬时应变
根据上述分级加卸载蠕变试验数据处理方法,各级应力水平下,岩石的瞬时应变由瞬弹性应变和考虑加载历史的瞬塑性应变构成。
图6为不同温度下红砂岩试件的瞬时应变与加载应力水平的关系曲线,由图6可知,红砂岩的瞬弹性应变εme和瞬塑性应变εmp均随应力水平的增加而增大,而同一应力水平下岩样的瞬弹性应变εme和瞬塑性应变εmp随温度的下降呈降低趋势,且该趋势随着应力水平的增长愈发明显。如在第2级应力水平下,S4,S7及S9岩样的瞬弹性应变分别为4.49×10-3,3.56×10-3,8.41×10-4,降低幅度分别为20.71%和76.38%,瞬塑性应变分别为2.58×10-3,1.40×10-3,8.09×10-4,降低幅度分别为45.74%和42.21%,而在第4级应力水平下,S7及S9岩样(此时S4岩样已破坏)的瞬弹性应变分别为6.23×10-3和1.59×10-3,降低幅度为74.48%,瞬塑性应变分别为1.96×10-3和1.03×10-3,降低幅度为47.45%,说明温度的降低能够有效抑制岩石的瞬时变形。
2.2.2黏弹性应变和黏塑性应变
蠕应变εc由黏弹性应变εce和黏塑性应变εcp组成。图7为不同温度下红砂岩试件的蠕应变、黏弹性应变、黏塑性应变与加载应力水平的关系曲线。
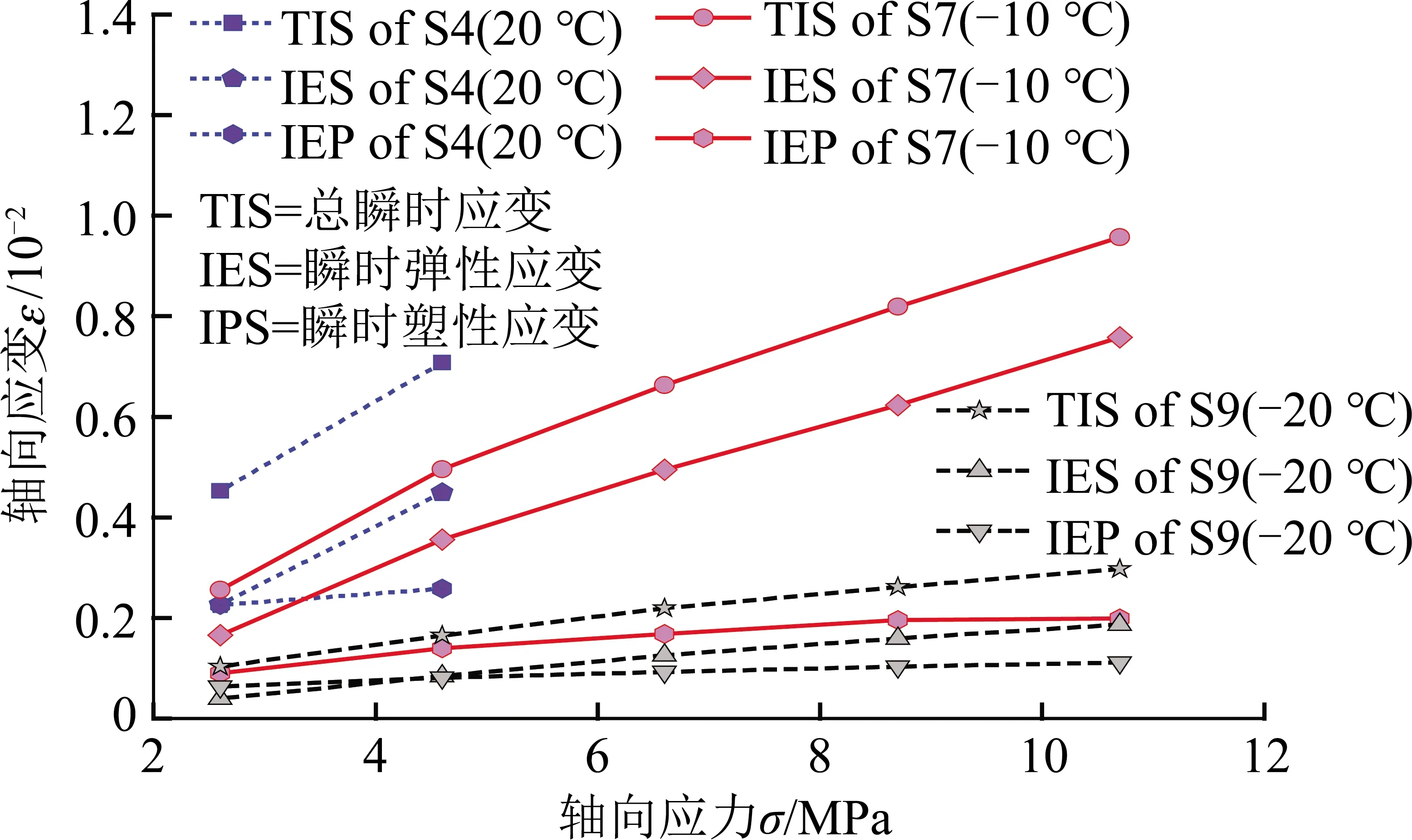
图6 瞬时应变与应力水平关系Fig.6 Curves of instantaneous strain versus stress
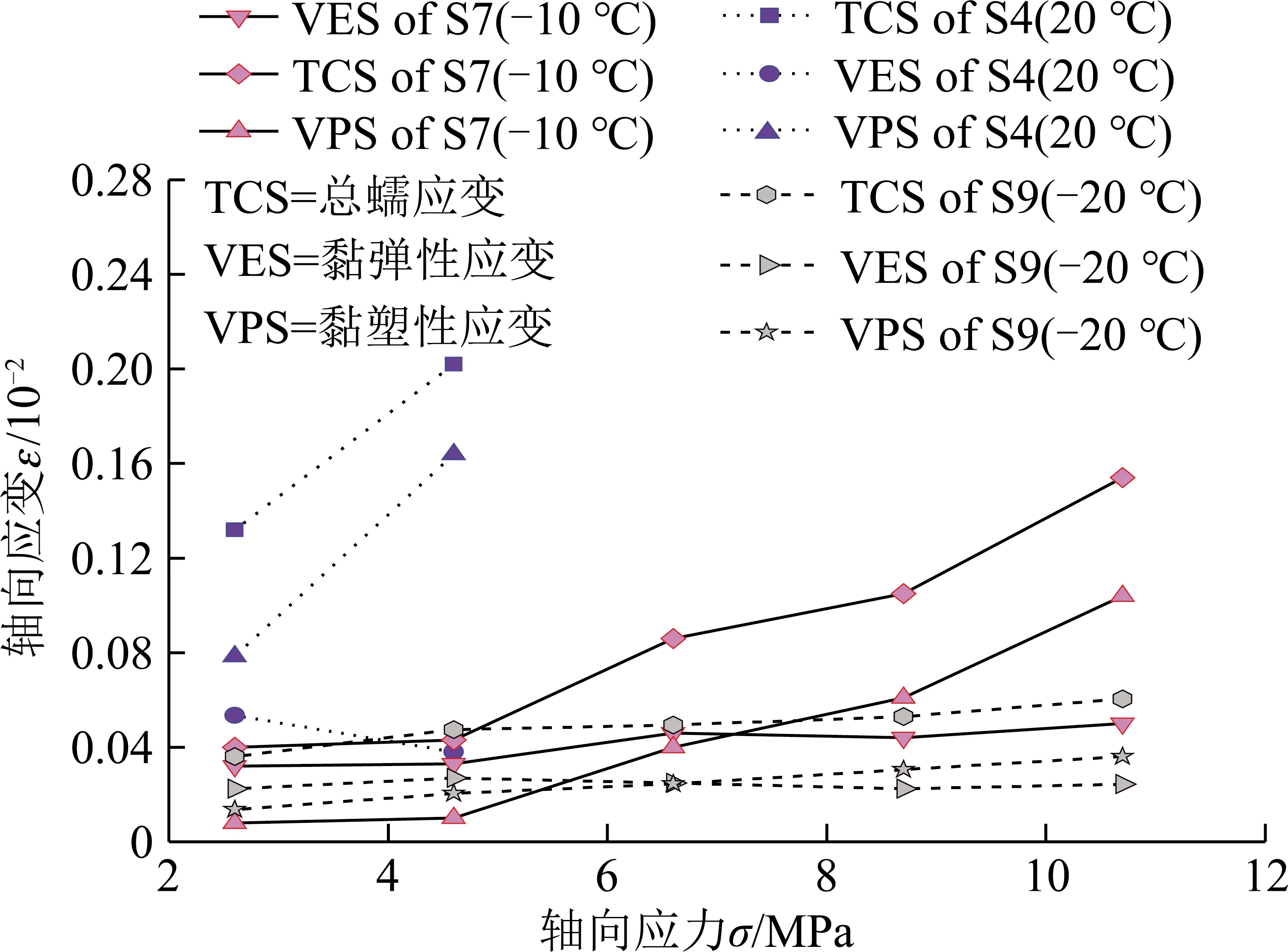
图7 黏弹性、黏塑性应变及总蠕变与应力水平关系Fig.7 Curves of total creep,visco-plastic and viscoelastic strains versus stress
由图7可知,红砂岩在同一应力水平下岩样的黏弹性应变εce和黏塑性应变εcp随温度的下降呈降低趋势。如在第4级应力水平下,S7及S9岩样(此时S4岩样已破坏)的黏弹性应变分别为4.40×10-4和2.24×10-3,降低幅度为49.09%,黏塑性应变分别为6.1×10-4和3.06×10-3,降低幅度为49.84%,说明温度的下降能够有效降低岩石的黏性变形。同时,黏塑性应变εcp均随应力水平的增加而增大,且蠕应变中黏塑性应变所占比例总体上有逐渐增加的趋势,以S9岩样为例,在第1~5级应力水平下红砂岩的黏塑性应变分别占总蠕变量的37.95%,43.25%,49.60%,57.74%,59.67%。这表明随应力水平的增加,岩石黏性流动性增强,同时,由于加载应力历史的累积作用,黏塑性应变增长迅速。在低应力水平下,岩石蠕变主要表现为黏弹性变形,黏塑性变形所占比例较小;随着应力水平的增大,岩石的蠕变变形表现为黏弹性和黏塑性共存的状态;在加速蠕变阶段(岩样在该级应力水平下破坏),如图8所示,黏弹性应变和黏塑性应变无法区分开来,可认为加速蠕变阶段的蠕应变全部是黏塑性应变,黏塑性应变随时间和应力历史的累积不断增长直至破坏,黏塑性应变的不断发展是岩体工程流变破坏的根本原因。

图8 岩样加速蠕变曲线Fig.8 Accelerated creep curves of rock sample
3 岩石非线性黏弹塑性流变模型
分数阶微积分是微积分中,用于解决建模难题的数学工具。相比于整数解微积分,分数阶微积分理论模型与试验结果吻合度较高,使用参数少,表述更为简洁,因此,在诸多领域得到应用,近年来也在岩石流变领域逐渐发展[16-18],分数阶微积分常采用Riemann-Liouvelle理论[19-20]进行定义。对于函数f(t)的n阶积分定义为
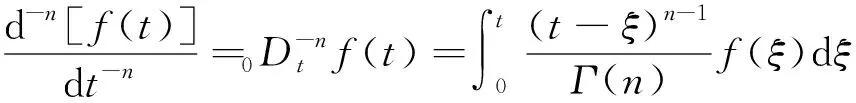
(12)
分数阶微分定义为

(13)
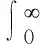
理想固体的应力应变关系满足Hooke定律,理想流体满足Newton黏性定律,而岩土体一般被认为是介于理想固体与理想流体的材料。因此,Scott-Blair[16]构造了一种新的本构方程:
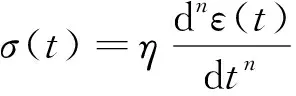
(14)
式中,η为黏弹性系数;0≤n≤1。
式(14)即为基于分数阶微积分的本构方程。当n=0时为理想固体,n=1为理想流体。通常采用介于理想固体和理想流体之间的软体元件(也称为Able黏壶)来描述这种黏弹性状态,如图9所示。

图9 软体元件Fig.9 Soft-matter element
当应力恒定时,即σ(t)=const,软体元件可以描述蠕变行为,对式(13)两边进行分数阶积分,根据Riemann-Liouville分数阶理论,可得
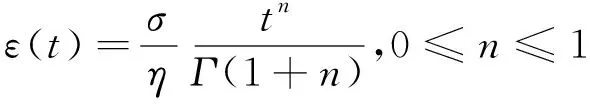
(15)
对于不同材料,可通过改变软体元件的参数η,n来调整蠕变曲线,从而使试验结果的拟合更加精准。
根据低温条件下的分级蠕变加卸载试验结果,引入软体元件,建立考虑温度影响的非线性黏弹塑性流变模型,以描述软岩的黏弹塑性流变特性。模型由瞬时弹性元件、瞬时塑性元件、黏弹性元件及黏塑性元件4部分组成,如图10所示。
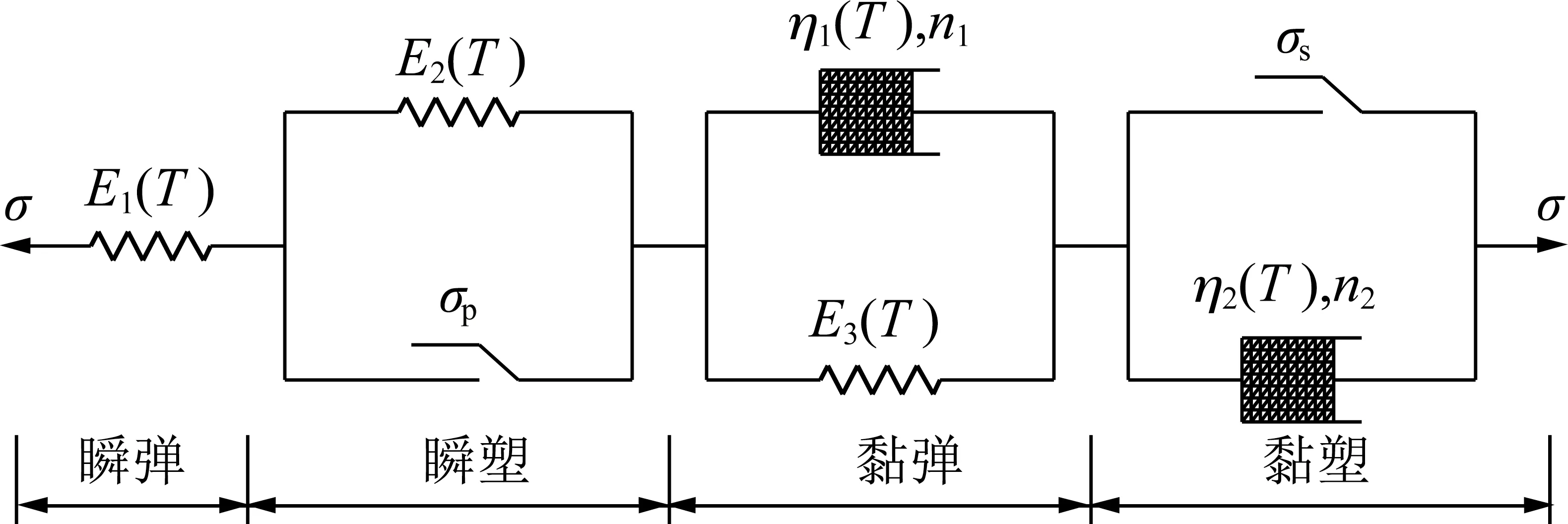
图10 考虑温度影响的岩石非线性黏弹塑性流变模型Fig.10 Nonlinear viscoelastic-plastic rheological model of rock considering temperature effects
3.1 瞬时变形元件
采用Hooke体(图11)来描述岩石的瞬时弹性变形,其本构方程为

(16)
式中,εme为Hooke体产生的应变分量;σ为轴向应力;E1(T)为瞬时弹性元件中与温度T有关的Hooke体弹性模量。

图11 瞬时弹性元件
Fig.11 Instantaneous elastic model

(17)
式中,εmp为瞬塑体的应变分量;σp为瞬时塑性元件中塑性滑块的应力阈值;E2(T)为瞬时塑性元件中与温度T有关的Hooke体的弹性模量。

图12 瞬时塑性元件Fig.12 Instantaneous plastic model
瞬时变形元件用于描述岩石在瞬时加载过程中产生的瞬时变形。瞬时弹性元件主要反映试验初期加载时,因瞬时加载而产生的瞬时弹性变形;随着加载应力水平的增大,当某一级加载应力大于瞬时塑性元件中塑性滑块的应力阈值σp时,岩石会因瞬时加载而产生塑性变形,这一变形量由瞬时塑性元件来描述。
3.2 黏弹性流变元件
黏弹性变形可以用软体元件与Hooke体并联的形式来描述,如图13所示。

图13 黏弹性元件Fig.13 Visco-elastic model
软体元件在受到应力后,反应不会像理想流体那样迅速,蠕变曲线不会产生陡变现象,因而可以更好地对试验曲线进行拟合。其本构关系为
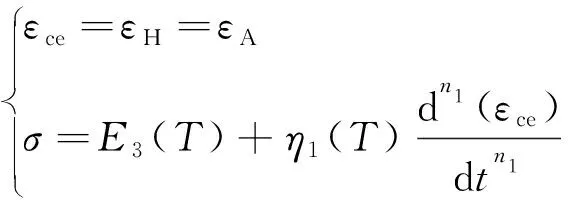
(18)
式中,εce为黏弹性应变;εH为Hooke体的应变;εA为软体元件的应变;E3(T)为黏弹性元件中与温度T有关的Hooke体的弹性模量;η1(T)为与温度有关的软体元件的黏弹性系数;n1为分数阶微积分的阶数,n1≤1。
根据分数阶微积分相关理论公式(7)进行求解可得
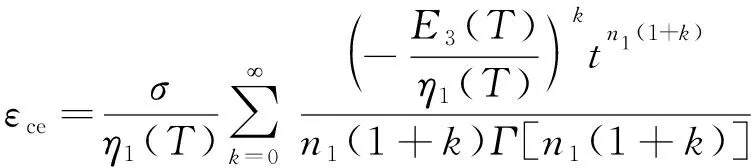
(19)
3.3 黏塑性流变元件
软体元件在n>1时,应变随时间显著增长,表现出加速流变的特征,且蠕变特性随着n的增大逐渐增强,因而可以采用软体元件与塑性滑块并联的黏塑性元件来描述岩石的黏塑性变形,从而更好的反映岩石的加速蠕变过程,如图14所示。

图14 黏塑性元件Fig.14 Visco-plastic model
根据式(4)及2元件并联原则,可得模型的应力应变关系为
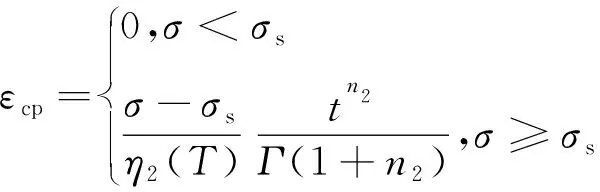
(20)
式中,n2为阶数,且n2>1;σs为黏塑性元件中塑性滑块的应力阈值。
综上所述,结合式(16),(17),(19),(20)可得非线性黏弹塑性蠕变方程为
当σ<σs时,ε=εme+εmp+εce即
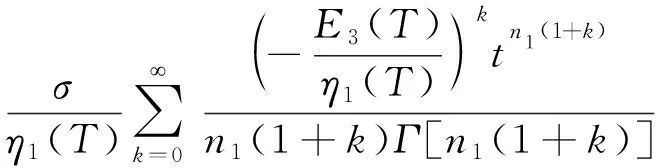
(21)
当σ≥σs时,ε=εme+εmp+εce+εcp即
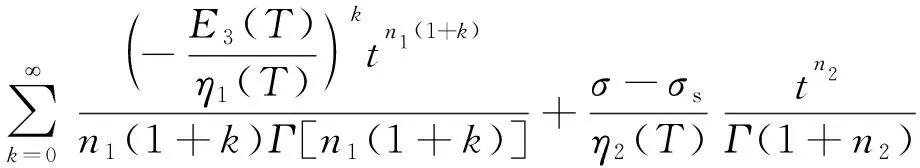
(22)
3.4 模型参数识别与验证
根据上述试验结果,对不同温度条件下红砂岩蠕变试验曲线进行模型参数识别。目前,模型参数识别的方法有很多,在非线性问题方面,采用最小二乘法进行参数识别最为普遍。然而,用最小二乘法进行参数识别时,因其对初始值的合理性要求较高,导致识别过程较为复杂且效果并不理想。
本文采用1stOpt数值优化计算软件进行模型参数识别,该软件广泛应用于各学科领域的非线性回归、曲线拟合及非线性复杂模型参数估算求解问题。软件内含多种经典及现代优化算法,其独创的通用全局优化算法(Universal Global Optimization),在保留局部算法快捷高效的同时,解决了经典算法对初值的依赖问题,拟合结果精准度更高。笔者利用软件内置的通用全局优化算法结合最小二乘法中的Levenberg-Marquarat算法对蠕变曲线进行拟合,当加载应力小于σs,即εcp=0时,采用式(21)对蠕变曲线进行模型参数辨识;当加载应力≥σs,即εcp>0,采用式(22)进行拟合并确定模型参数。因篇幅有限,此处只对各温度条件下最后一级蠕变曲线进行拟合,拟合结果见表2,其中,R2为相关系数。

表2 模型参数拟合结果Table 2 Model parameters determined by fitting analysis
图15为不同温度条件下红砂岩蠕变试验结果及模型拟合曲线。可以看出,本文所提出的理论模型能够很好的描述不同温度条件下试验结果,尤其是加速蠕变阶段,且拟合度较高,这也说明了本文所建立非线性黏弹塑性模型的正确性与适用性。
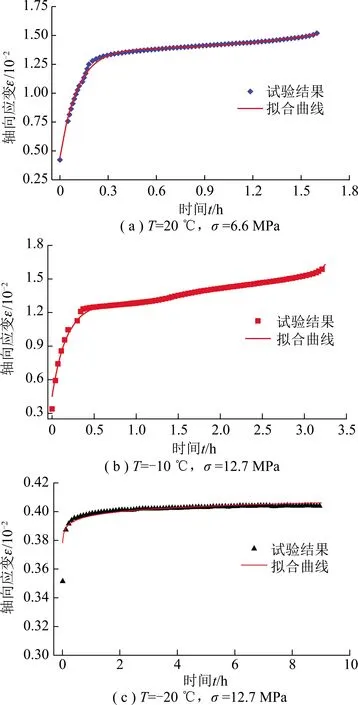
图15 不同温度下红砂岩蠕变试验结果及模型拟合曲线Fig.15 Creep test data and model fitting curves of red sandstone at different temperatures
3.5 低温对模型参数的影响
从表2可以看出,随着温度的降低模型参数E1(T),E2(T),E3(T),η1(T),η2(T)均有不同程度增长,对表2中各项参数与温度的关系进行拟合,得到模型各项参数与温度的关系如下:

(23)
式(23)为温度与模型参数之间的函数关系,将其代入式(21),(22),即可得到不同温度条件下的红砂岩蠕变方程。图16为E1(T),E2(T),E3(T)及η1(T)与温度关系的拟合曲线,从式(23)及图16可以看出,除弹性模量E3(T)外,其它模型参数均随温度的降低呈指数型增长。当温度在20~0 ℃时,除弹性模量E3(T)外,模型参数均变化不大;0~-10 ℃时,模型参数随温度的降低逐渐增长;当温度为-10~-20 ℃时,随着温度的降低,模型各项参数迅速增长,且增长幅度尤为显著。表明低温对岩石有明显的硬化作用,从而减缓加速蠕变的发生。这一现象也可由图5看出,温度为20 ℃时岩样S4在第3级就产生加速蠕变,-10 ℃时S7岩样在第6级产生加速蠕变阶段,而-20 ℃时岩样S9在第6级时仍无明显的加速蠕变特征。

图16 各模型参数与温度拟合曲线Fig.16 Fitting curves of model parameters and temperature
4 结 论
(1)低温作用下红砂岩表现出典型的蠕变3阶段特征:衰减蠕变、稳态蠕变和加速蠕变;其总应变量由可恢复的瞬弹应变、黏弹性应变和不可恢复的瞬时塑应变、黏塑性应变4部分组成,表明低温红砂岩具有弹、黏、塑共存的特性。
(2)红砂岩的瞬时应变随应力水平的增加而增大,随温度的下降显著降低,且瞬弹性响应呈近线性;黏弹性应变和黏塑性应变随温度的下降呈降低趋势。黏塑性应变随应力水平的增加而增大,且蠕应变中黏塑性应变所占比例逐渐增加。
(3)根据红砂岩蠕变特性,引入分数阶微积分,将软体元件与弹、塑性元件并联后与其他元件串联,建立考虑低温影响的非黏弹塑性流变模型。该模型可以很好的描述红砂岩蠕变的3个阶段,尤其是加速蠕变阶段。采用通用全局优化算法结合最小二乘法中的Levenberg-Marquarat算法对不同温度条件下的蠕变曲线进行拟合分析,得到不同温度条件下的模型参数。
(4)对不同温度条件下的模型参数进行分析,得到低温对模型参数的影响规律。研究发现,随着温度的降低,除弹性模量E3(T)外各模型参数均呈指数增长,且在-10~-20 ℃时,增长幅度尤为显著。
