基于Bertalanffy时间函数的地表动态沉陷预测模型

2020-09-16徐乃忠孙万明邓伟男韩科明

煤炭学报 2020年8期

高超，徐乃忠，孙万明，邓伟男，韩科明

(1.煤炭科学研究总院开采研究分院，北京 100013; 2.天地科技股份有限公司开采设计事业部，北京 100013)

地表沉陷是一个非常复杂的时间-空间运动问题，地表任意时间段内的变形量值若达到地表建(构)筑物的极限承受值，将可能诱发地质灾害，威胁到地面人员的生命与财产安全。为准确科学地评估工作面开采对地面沉陷的影响程度，需要事先建立科学的地表沉陷动态沉陷预计模型，获得该地区准确的模型参数，进而分析地表任意点、任意时刻的地表动态沉陷变形量。国内外相关学者针对不同的动态沉陷预计模型进行了探索。

1952年，波兰学者KNOTHE[1]基于“某一时刻的地表下沉速度与地表最终下沉值之差成比例”原理推导了Knothe动态下沉时间函数。崔希民等[2]通过实测资料对比研究得出Knothe时间函数地表移动下沉速度、下沉加速度与地表移动变形的实际过程的差异性。常占强等[3]基于Knothe时间函数改进并提出了分段Knothe时间函数模型;后续张兵等[4]对该函数进行了优化。刘玉成等[5]针对Knothe时间函数的不足，提出幂指数-Knothe时间函数模型。王军保等[6]将S型生长曲线MMF模型用于地表沉降时间预测中。王正帅与邓喀中[7]将Richards生长模型引入地表沉降预计中，分析了模型参数与地质采矿条件之间的定性、定量关系。高延法等[8]基于Knothe时间函数，导出了适用于地表移动衰退期及其以后的地表下沉衰减函数并对沉陷区的稳定性进行了分类。胡青峰与崔希民等[9]对Knothe时间函数的各参数规律进行了分析。彭小沾与崔希民等[10]对Knothe时间函数、Sroka-Schober时间函数的优缺点及其相互关系进行了详细分析。刘玉成[11]将概率积分法与Weibull时间函数相结合，构建了沉陷主剖面线的地表动态下沉函数模型。朱广轶等[12]运用概率积分法提出地表动态移动变形的坐标-时间函数。张文志与邹友峰等[13]将Logistic模型引入矿区单点动态沉陷预计中，并通过实测数据分析了模型的精度与适用性。李德海[14]将覆岩岩性与Knothe时间函数中的参数相结合，探讨了覆岩岩性与时间影响参数的关系。余闯等[15]将Gompertz函数引入路堤沉降预测中，并结合相关实践证明了该函数的适用性。

沉陷动态预计一般由开采引起的最终地表移动变形乘以反映岩层移动时间效应的时间函数模型来进行，该时间函数往往由实测数据拟合求得。受测量精度的限制，开采沉陷学中，规定的地表初始移动时间t=0时的地表下沉值为10 mm，以往学者大多以通过原点的函数作为动态沉陷预计函数，并基于实测成果反算求得各模型中的参数值，沉陷实测-理论模型构建-实践应用的过程，往往由不对应的时间函数带来一定误差。

大量的实测资料表明，Knothe,Logistic等时间函数与实际的地表沉陷的动态过程不完全符合，不能科学地描述地表动态下沉过程。笔者基于朔州地区特厚煤层高强度综放开采的地表移动变形的特殊性，在分析常用时间函数地表点沉陷变形的特征基础上，引入Von Bertalanffy时间函数，基于此函数改进该函数，使之成为三参量的时间函数，并应用Matlab拟合求取各参数，最后基于该模型并结合概率密度影响函数对井工一矿高压线塔下回采进行地表动态沉陷计算分析，并成功指导地面线塔的基础加固与纠偏治理。

1 动态沉陷时间函数

在许多时间序列预测中常用“S型”曲线描述事物的增长或衰减过程，由于“S型”曲线形式多样、结构不同，对同样观测值预测结果略有差别。在时间序列里，有些变量的增长量最初比较小，随时间的增加逐渐增长而达到一个快速增长时期，而后增长速度趋缓，最终达到稳定的总增长量，这一过程若用曲线来表示，则是一种沿时间轴方向拉长的“S型”曲线。

1.1 常见函数模型

若用wm表示地表任意点沉陷稳定后的最大下沉量(单位为mm)，w(t)表示任意时刻的动态下沉，v(t)表示任意时刻的地表下沉速度(单位为mm/d)，a(t)表示任意时刻的地表下沉加速度(单位为mm/d2)。

(1)Knothe函数。该模型假定地表下沉速率dW(t)/dt与地表最终下沉值wm和某一时刻t的动态下沉值w(t)之差成比例，推导并提出:

w(t)=wm(1-e-ct)

(1)

式中，c为时间影响参数，与采场覆岩岩性有关。

为进一步研究该模型在煤矿开采沉陷预计中的适用性，对该函数进行一阶和二阶函数求导，分析该下沉速度v(t)=wmce-ct和下沉加速度a(t)=-wmc2e-ct的函数，可知Knothe时间函数具有以下特征:① 地表下沉曲线形状非“S型”;② 地表刚开始受到沉陷扰动，即t=0时下沉速度最大，然后逐渐减小至0;③ 下沉加速度恒为负值，下沉加速度一开始以最大加速度逐渐衰减;④ 仅有1个参数c，实际的动态沉陷表达性不足。

(2)Logistic模型。Logistic增长模型[13]在生态学、人口学等领域得到广泛地应用;它反映了事物发生、发展、成熟并趋于饱和(极限)的过程。其函数式为

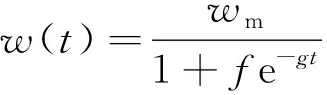
(2)

式中，g,f为与采场上覆岩层岩性有关的参数。

(3)Gomepertz模型。由英国数学家B.Gomepertz提出并应用于动植物的消亡规律，现多用于非采动影响下的路堤或地基的沉降，其函数式[15]为

w(t)=wme-e-ct+d

(3)

式中，c,d为与采场上覆岩层岩性有关的参数。

对该函数进行一阶和二阶函数求导，分析该下沉速度v(t)=wmce-ed-cted-ct和下沉加速度a(t)=-wmc2e-ct的函数，可知Gomepertz时间函数具有以下特征:① 下沉曲线是“S型”，与煤矿开采地表沉陷特征较相符;② 地表移动初始期，t=0时，地表下沉速度v≠0、下沉加速度a≠0，这与实际情况不符。

(4)Weibull模型。Weibull曲线函数在软土地基的沉降预测中适用性较好，其函数式[11]为

w(t)=wm(1-e-ntk)

(4)

式中，n,k为与采场上覆岩层岩性有关的参数。

对该函数进行一阶和二阶函数求导，分析该下沉速度v(t)=wmnktk-1e-ntk和下沉加速度a(t)=wmnke-ntk[(k-1)tk-2-nkt2k-2]的函数，可知Weibull时间函数具有以下特征:① 该函数是对Knothe时间函数的改进;② 收敛速度较快，衰退期的下沉“拖尾”性质表现不足;③ 时间函数中的参数物理意义尚不明确，难推广。

(5)Richards时间函数。Richard生长方程[7]为一个3参数的非线性方程，主要用于生物生长的预测，其函数方程为

w(t)=wm(1-b1e-b2t)1/(1-b3)

(5)

式中，b1为初始沉降值参数;b2为初始沉降速度参数;b3为曲线形状参数。

对该函数进行一阶和二阶函数求导，分析该下沉速度和下沉加速度的函数，可知Richard时间函数具有以下特征:① Richards函数可较好地表达煤矿开采后地表点任意时刻的下沉、下沉速度、下沉加速度等;② 参数对曲线形状影响敏感性差，不同采矿地质条件下曲线形状变化规律性不明显。

(6)双曲线模型。双曲线函数模型主要用于预测地基和路基的沉降，其函数模型在一定程度上可反映次固结的影响。

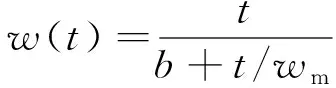
(6)

式中，b为与采场上覆岩层岩性有关的参数。

对该函数进行一阶和二阶函数求导，分析该下沉速度v(t)=b/(b+t/wm)2和下沉加速度a(t)=-2b/[(b+t/wm)3wm]的函数，可知双曲线时间函数具有以下特征:① 地表动态下沉曲线形状非S型;② 与Knothe等时间函数相似，t=0时，下沉速度最大，然后逐渐减小为0;③ 下沉加速度恒为负值，然后逐渐衰减为0。

(7)分段Knothe时间函数。

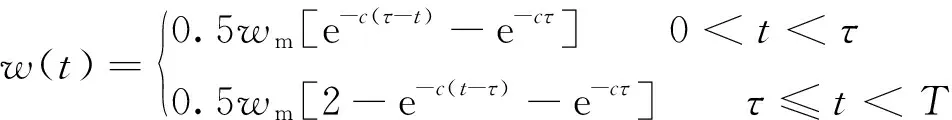
(7)

式中，c为与采场上覆岩层岩性有关的参数;T,τ分别为地表总移动周期与地表下沉速度达到最大的时刻。

与Knothe函数相似，但其又有新的特点:① 人为对时间函数进行分段划分，当最大下沉速度时的τ时刻时，地表下沉值并非为1/(2wm)，与实际情况的相差较大;② 下沉的加速过程和减速过程是对称的，没有反映出沉陷中活跃期的快速性、衰退期的长期性和拖尾性。

(8)幂函数-Knothe时间函数。考虑到岩层与地表移动的非线性过程，在Knothe函数式中增加一个幂级系数k。

w(t)=wm(1-e-ct)k

(8)

式中，c,k为与采场上覆岩层岩性有关的参数。

分析下沉速度v(t)=wmcke-ct(1-e-ct)k-1和下沉加速度a(t)=wmc2k(2e-2ct-e-ct)(1-e-ct)k-2的函数，可知双曲线时间函数具有以下特征:① 在Knothe函数的基础之上，增加了幂级系数k，可以适当的改变下沉曲线的形状;② 在一定程度上克服了Knothe时间函数某些方面缺点，但缺少地表下沉速度对函数的控制影响研究。

(9)MMF时间函数模型。MMF模型是于1975年提出是一种“S型”生长曲线模型，王军保等[1]将该模型用于地表沉降时间预测中。

(9)

式中，c,b为时间影响参数，与采场覆岩岩性有关。

对该函数进行一阶和二阶函数求导，分析该下沉速度v(t)=wmbctb-1/(c+tb)2和下沉加速度a(t)=wmbctb-2(ba-c-btb-tb)/(c+tb)3的函数，可知MMF函数具有以下特征:① 该函数可以较好地表示不同地质采矿条件下的地表下沉;②b与c的物理意义有待研究;③ 时间t=0时下沉速度和加速度都无法表示。

(10)Sroka-Schober时间函数。Sroka以Knothe函数为基础建立的时间函数为

(10)

式中，f为岩层的相对收敛率;ξ为上覆岩层的时间系数，用于描述岩层的滞后效应。

该函数具有以下特征:① 该函数曲线非S型;② 下沉速度更接近于理想的时间函数，但下沉加速度曲线形态不正确;③ 实际应用中，f和ξ不是已有参数，参数难以获取，并且f和ξ难以同时求出。

大量的实测资料表明，Knothe,Logistic,Gomepertz与Weibull等常见时间函数与实际的地表沉陷的动态过程不完全符合，这些函数虽能在一定程度上对地表动态移动变形进行预计，但这些模型或不能反映地表下沉速度和加速度的变化规律，或函数中的参数物理意义不明确，不能反映各参数随地质采矿条件的变化。

1.2 理想函数模型特征

理想的时间函数模型应该能够反映:工作面回采尺寸逐步增大，岩层移动变形传播至地表，地表在可监测范围内随时间变化应为规律性地移动变形。依据煤矿开采后地表移动变形的动态变形实测情况，结合前述学者对地表动态沉陷时间函数的研究成果，理想的时间函数模型应具有以下特点:①t=0时，地表某点的下沉量w(t)=0或为可监测值(受监测精度限制，一般取值为10 mm)、下沉速度v(t)=0、下沉加速度a(t)=0;② 在初始期的下沉量、下沉速度与下沉加速度较小、为正值且逐渐增大;③ 活跃期下沉速度与下沉加速度较大，下沉加速度变化过程为先增大至峰值后、逐渐减小至0、然后负值、负值达到峰值后逐渐减小;④ 衰退期下沉速度为正、逐渐变小且逐渐趋于0，下沉加速度由负值逐渐增大且逐渐趋于0;⑤ 整个下沉-时间曲线近似“S”型曲线，由于岩块与裂隙的压实、蠕变历时较长，衰退期长而平缓;⑥ 针对不同地质采矿条件，可通过形状参数调整动态下沉曲线形状的陡峭或平缓、可通过调整沉降速度参数调整地表动态下沉速度。

2 基于Bertalanffy的时间函数模型

2.1 模型及其改进

Von Bertalanffy模型[17-18]为常见的生物生长模型，主要用于预测动植物的生长规律，也常应用于经济与统计学中。该模型是Logistic的推广，且具有较好的灵活性，其函数方程为

w(t)=wm(1-be-ct)3

(11)

式中，b与c为时间影响参数，其中b可反映t=0时的初始沉降值，c反映t=0时的初始沉降加速度值。

模型改进(三参模型):考虑到岩层与地表移动过程的非线性，尤其对于近浅埋深特厚煤层综放开采，地表沉陷变形集中、盆地边缘陡峭等特征，将Bertalanffy函数式中的3次幂变为时间影响参数d(反映曲线的形状，可反映不同地质采矿条件下的曲线陡峭、收敛速度、拖尾性等)，用于煤矿开采地表动态沉陷研究中，可将Bertalanffy函数改进为三参数模型:

w(t)=wm(1-be-ct)d

(12)

根据模型中参数对曲线形态或量值的控制性作用，式中的参数b为初始沉降值参数(可反映地表初始沉降值及地表移动初始期的长短)，c为初始沉降速度参数，d为曲线形状参数。

2.2 模型特点分析

2.2.1不通过原点性

煤矿开采地表沉陷动态预计的实际应用中，在选择好模型情况后，将实测参数代入函数模型，反算求得各参数。在实际“三下”采煤或沉陷保护应用中，受测量精度的限制，开采沉陷预计参数求取及沉陷预计所涉及的边界角、超前影响角等都是基于地表下沉量值为10 mm点作为计算依据的。即多个角量参数通常以地表下沉量达到10 mm为地表移动起算点，t=0时，地表下沉取值w(0)=10 mm。

Knothe时间函数的收敛速度随地质采矿条件的调整性较差，仅通过一个参数c很难进行调整;在e-ct项之前缺少一个沉降初始值的控制参数，改进Bertalanffy三参数函数将这个缺陷进行了补充。

2.2.2“S型”曲线特征

为进一步研究该模型在煤矿开采沉陷预计中的适用性，对该函数进行一阶和二阶函数求导(各函数的时间函数曲线如图1所示)。

v(t)=wmbcd(1-be-ct)d-1e-ct

(13)

a(t)=wmbc2de-ct(1-be-ct)d-2(bde-ct-1)

(14)

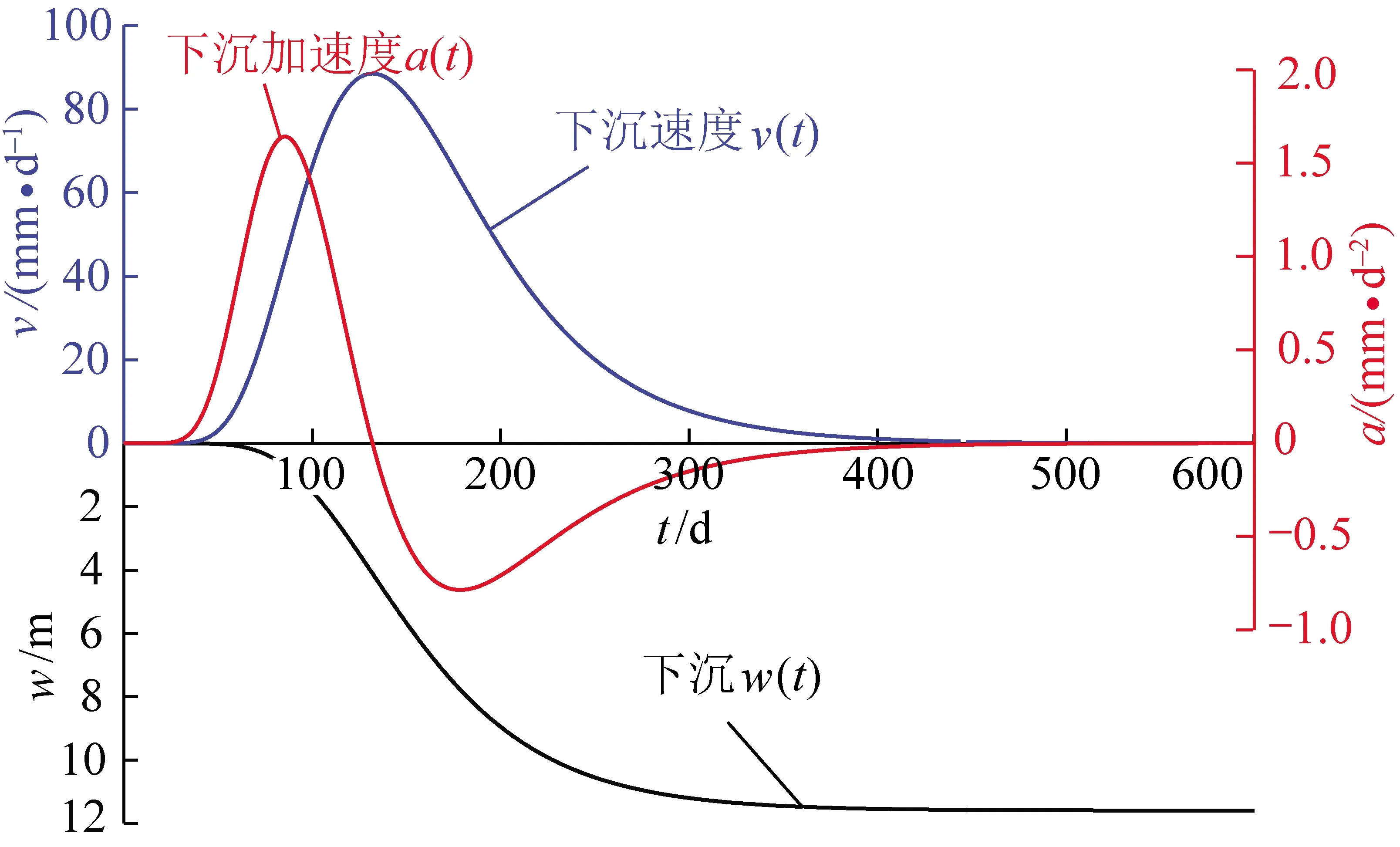
图1 改进Bertalanffy三参数模型动态下沉、下沉速度及下沉加速度时间函数Fig.1 Dynamic subsidence,velocity and acceleration time function of improved three-parameters model

结合图1所示的形态曲线，分析改进Bertalanffy三参数时间函数的动态下沉、下沉速度和下沉加速度时间函数，具有以下特征:

(1)单调性。因参数b,c与d均为正值，(1-be-ct)d>0，所以w(t)是t的增函数。

(2)凹凸性。令w″(t)=a(t)=0，求得拐点的时间坐标t=ln(bd)/c，此时w(t0)=wm(1-1/d)d，并且当tt0时，下沉曲线是“凸”的;即w(t)为时间t的“S型”曲线。

(3)渐进性。为有界函数，渐近线为w(t)=wm。

2.3 模型参数讨论

依据多个煤矿地表移动变形实测数据表明，改进Bertalanffy三参模型参数与地质采矿条件关系密切，不同的采深/采厚比值、采动充分程度、控制沉陷的关键层破断位置高度、工作面推进速度等因素，地表移动变形越剧烈程度、地表移动的初始期与活跃期的时间跨度、地表点的动态下沉速度、动态下沉加速度有一定的差异。Bertalanffy改进三参模型中的参数取值亦可通过相应调整适应不同地质采矿条件下的地表动态变形计算。

2.3.1初始沉降参数b

改进Bertalanffy三参模型中参数b反映t=0时的初始沉降值与地表移动初始期的长短。b的经验取值范围(0,1]，当b=1时，函数可通过原点;相同地质采矿条件下，工作面推进速度越快，地表移动越剧烈，b越大。该参数的变化规律如图2所示(图中各曲线的其他变量c=0.032 5，d=36)。

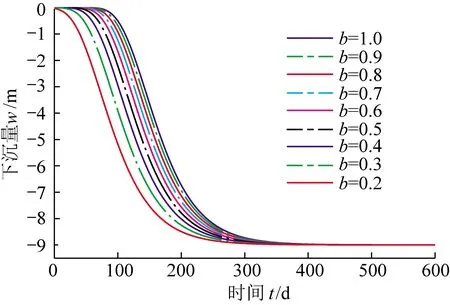
图2 初始沉降参数b对模型的影响规律Fig.2 Influence law of initial settlement parameter b

2.3.2动态沉降加速度参数

c反映t=0时的初始沉降加速度值。c的经验取值范围[0.005,0.500];地表及覆岩移动变形越剧烈(工作面推进速度越快等因素)，地表动态沉降加速度越大，曲线越陡，c值越大;反之，地表移动剧烈程度越低，c值越小。该参数的变化规律如图3所示(其他变量b=0.992 0，d=36)。

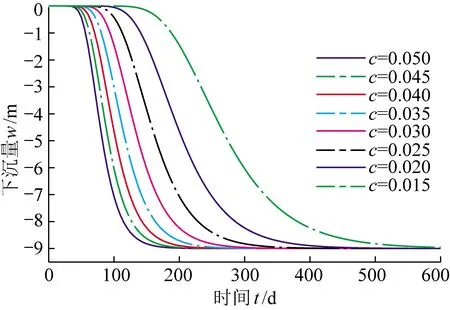
图3 加速度参数c对模型的影响规律Fig.3 Influence law of acceleration parameter c

2.3.3形状系数d

d反映S型曲线的形状，可反映不同地质采矿条件下的地表动态下沉初始期的长短、沉陷收敛速度与拖尾性等。d的经验取值范围为[1,100];曲线形状控制参数d越大，地表初始期越长，受采动影响反映至地表的时间越长;同时d越大，地表收敛速度越小，地表移动延续时间越长;当d=1时(同时b=1)，即为常见的Knothe时间函数。该参数的变化规律如图4所示(其他变量b=0.992 0，c=0.032 5)。

图4 形状系数d对模型的影响规律Fig.4 Influence law of curve shape factor d

3 参数拟合求取与动态沉陷应用验证

3.1 研究区域地质采矿及观测站概况

研究区域东坡煤矿位于山西朔州市，井田内覆盖有40～60 m厚的黄土，914走向长壁工作面开采9号煤，工作面倾向长约240 m，连续推进长度约1 250 m，开切眼处平均采深265 m，平均采出煤层厚度为14.4 m;采煤方法为特厚煤层综放一次采全高，平均煤层倾角2.3°;工作面推进速度约为2.8 m/d，开采强度较大[19-20]。

914工作面A测线为走向半盆地观测线，总长约为480 m，布置测点24个;自2011年11月至2014年5观测15次，历时约30个月。

3.2 时间函数求参及拟合优度分析

拟合优度是指回归曲线对观测值的拟合程度;度量拟合优度的统计量是可决系数(亦称确定系数)R2;R2取值范围为(0,1)，R2越接近1，说明回归曲线对观测值的拟合程度越好，反之R2值越小，拟合程度越差。对于元素个数为n的序列Yi，拟合值为yi，则拟合优度R2可表示为

(15)

根据东坡煤矿A测线25号测点地表移动观测站的实测数据，应用Matlab对改进Bertalanffy三参模型时间函数进行曲线拟合求参，同时与Knothe时间函数作对比。

3.2.1Knothe时间函数

Knothe时间函数是我国煤矿动态沉陷预计中应用最早也是最为常见的时间函数，东坡煤矿A测线25号测点实测数据拟合求取的Knothe时间函数(图5)为

w(t)=wm(1-e-0.005 7t)

(16)

图5 25号测点不同时刻地表下沉曲线Fig.5 Subsidence curves at different times of No.25 points

Knothe时间函数中仅有一个参数c，不能有效地对“S型”动态下沉曲线形态、下沉加速度的曲线陡峭程度及初始沉降数值进行调整。25号测点应用Knothe时间函数的拟合优度R2为0.817。

3.2.2改进Bertalanffy三参模型时间函数

现实实测中时间t=0对应下沉等于0 mm的时刻受监测精度的限制，难以捕捉，实际应用中若仍基于过原点的时间函数进行拟合求参，再将该函数应用于动态沉陷预计工作中，这一过程将对时间函数有一定的误差影响;改进Bertalanffy三参模型时间函数可不经过原点(初始沉降值参数b=1时，可经过原点)，并将(t0=0,w0=0)=(0,10)作为时间函数的初始值进行拟合求参(图5)，25号测点应用改进Bertalanffy三参模型时间函数拟合优度R2为0.984。拟合求取的改进Bertalanffy三参模型时间函数为

w(t)=wm(1-0.992e-0.032 5t)36

(17)

由图5可直观地看出改进Bertalanffy三参模型时间函数模型与实测值很接近;应用Knothe时间函数的拟合优度R2为0.817，应用改进Bertalanffy三参模型时间函数拟合优度R2为0.982;后者时间函数相对误差较小，同时该模型中3个参数均被赋予了不同的物理意义，各个参数变化均与地质采矿条件有一定程度的联系。该时间函数模型方便简洁、符合理想时间函数模型的要求，可较好地模拟采动区地表动态沉降过程，能够计算出地表移动持续时间和地表点在某一时刻的下沉值、下沉速度、加速度等动态参数，且模型的可塑性较强，具有较广泛的适用性。

3.3 高压线塔受动态沉陷影响现场验证

随着高压输电网的规模化建设，高压线塔下伏煤炭开采及对地面线塔的动态变形影响与抗采动治理工作越来越受到重视。中煤平朔井工一矿试验工作面采煤工艺为特厚煤层综放开采，开采4号煤，机采高度为3.2～3.5 m，平均采出煤厚为8.7 m;工作面中部对应地表有1个基塔，线塔附近工作面采深为200～260 m，开切眼侧工作面平均推进速度为4.2 m/d。井工一矿与东坡煤矿工作面最近平面距离约2 km。

对于高压线下采煤地面控制变形一般可分为井下特殊采煤控制与地面线塔加固与纠偏措施。为保证高压线压覆煤炭的安全回采，首先基于地表动态沉陷变形预计，对线塔周边一定范围(沿工作面推进方向的开切眼侧60 m、沿工作面推进方向的终采线侧30 m、工作面回采巷道两侧各50 m)采取只采不放的措施。地面线塔为4个独立体基础，平行工作面推进方向(垂直于线路延伸方向)的两个基础间距为10 m，沿工作面推进方向的两个基础间距为8 m;为提高线塔的抗采动能力，将线塔原独立基础加固改造为钢筋混凝土连体的“井字形”基础，同时实现工作面开采过程中的纠斜。

参考岩性对地表沉陷的影响规律[21]，结合2个矿井差异，依据改进Bertalanffy三参模型时间函数各参数随地质采矿条件的差异规律(4号煤层位于9号煤层的上部，比9号煤层工作面地表移动初始期短、盆地边缘相对平缓;同时4号煤试验工作面采厚约8.7 m，比东坡煤矿914工作面平均采厚为14.4 m的数值小)，对各参数进行适当调整，井工一矿试验工作面选用的动态下沉时间函数为

w(t)=wm(1-0.994e-0.152t)32

(18)

考虑到部分区域的只采不放范围，结合工作面推进速度，对试验工作面沿水平方向将采出煤层厚度8.7 m，划分为机采高度部分3.2 m和放煤高度部分5.5 m，地表下沉系数取值q=0.83;根据实测资料当工作面超前线塔约96 m时，线塔地表首次扰动，t=0;当工作面超前线塔为60 m时，t=8.6 d;当工作面推过线塔30 m时，t=21.5 d，因此井工一矿试验工作面的动态下沉时间函数分段表述为

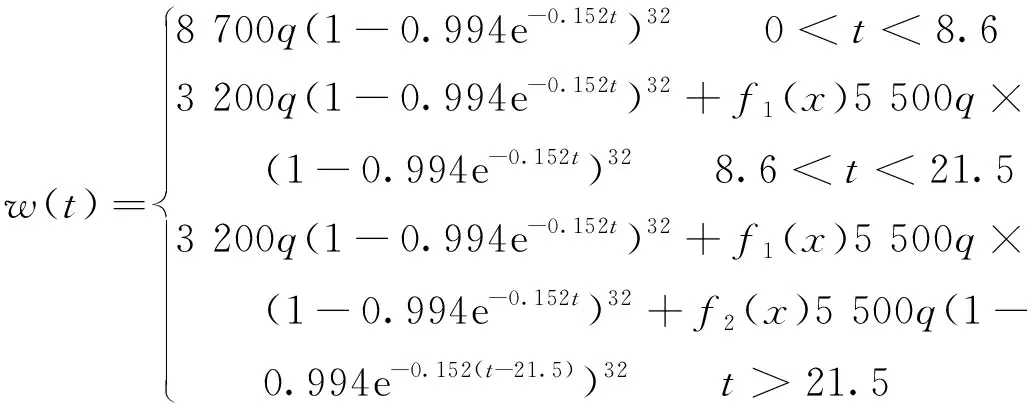
(19)

其中，f1(x)与f2(x)为线塔开切眼侧和终采线侧距离线塔为x时设计规划的放煤部分对线塔处的影响函数，如图6所示。

图6 线塔两侧放煤区对线塔的影响函数Fig.6 Influence function of top coal caving area on tower

线塔两侧放煤部分距离线塔越近，对线塔的采动影响越大，反之越小;其中f1(x)与f2(x)可由含主要影响半径r的函数表示为

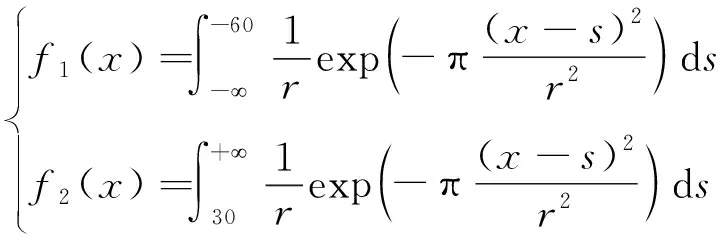
(20)

借鉴东坡煤矿实测资料及岩移数据成果取tanβ=2.6，则r=96 m，代入式(20)并经积分运算可求得f1(x)=0.059，f2(x)=0.217。应用式(19)所示的分段函数绘制的地表动态下沉曲线与线塔基础的实测值对比情况如图7所示。

图7 时间函数+影响函数法的变采高地表动态沉陷曲线Fig.7 Dynamic surface subsidence curve of variable mining height based on time function and influence function method

由于式(20)仅考虑了沿工作面推进方向的各影响函数叠加，无法对只采不放段x=(-60,30 m)沿工作面布置方向放煤段对影响函数的影响数值;同时特厚煤层综采放顶煤开采工艺复杂性，采放煤层厚度不容易控制等;图7绘制的基于影响函数的变采高地表动态沉陷曲线与实测数据相比虽有一定误差，但在实践生产中，应用该思路安全有效地采出了线塔压覆煤炭资源，并应用基于影响函数结合改进Bertalanffy三参模型时间函数指导线塔的动态倾斜纠偏，为该类工作提供借鉴意义。