基于组合体力学模型的固井水泥石封隔能力分析

王海柱， 石鲁杰， 郑 永， 张诚成

(中国石油大学(北京) 油气资源与探测国家重点实验室， 北京 102249)

我国页岩气储量丰富，具有广阔的开发前景.目前页岩气井开发手段主要是水平井与多级分段压裂技术相结合，而水平井压裂过程中易造成套管内压的大幅度波动，从而改变水泥石的受力状态，加剧水泥石封隔能力失效的风险.目前国内外学者主要从套管-水泥石-地层组合体受力情况、水泥石形变情况、固井界面胶结情况三个方向对固井水泥石封隔能力进行研究.

套管-水泥石-地层组合体受力研究经历了从单纯分析套管受力[1]到分析组合体整体受力[2]、从单纯借助井筒力学方程到综合使用多种理论与实验方法[3-6]的演变.组合体受力研究已经成为解释井下作业现象、并揭示其内在原理的主要手段，但是组合体力学状态与固井水泥石封隔能力的关系仍没有被准确地揭示出来.

水泥石形变的研究目的是探究水泥石材料变形规律，与组合体受力研究的主要区别在于该方向研究不通过力学方程而是借助实验手段研究水泥石的收缩程度、弹性模量、围压、水泥组分等因素对变形程度的影响.通过水泥石形变实验现象，可以研究水泥石胶结特性和水泥石微环隙[7-9]产生规律，从而为封隔能力预测提供指导.

固井界面的胶结情况是人们关注的重点，目前最常用的研究方法是通过声波测井对固井两胶结面进行测量并解释.声波测井方法简单有效但难以揭示固井界面胶结变化的内在机制，为此学者们多通过室内模拟实验的方法揭示水泥石胶结规律.1993年Jackson等[10]设计一套水泥石气窜检测装置，使用循环改变套管内压并检测固井两界面是否产生气窜通道的方法对水泥石胶结能力进行研究，其实验发现气窜通道总是在套管内压卸载时产生；2007年Garnier等[11]通过模拟实验认为单独的水泥石抗压强度难以衡量水泥石胶结能力，建议在胶结能力评价标准中引入弹性模量和破坏准则；2011年王克诚等[12]对受泥饼影响的水泥石胶结能力进行了实验研究，其认为地层渗透性、环空压差及地层流体扰动共同影响着套管-水泥石界面水力封隔能力；2019年Vralstad等[13]对受套管内压的水泥石进行实时CT扫描，研究了不同弹性模量水泥石的胶结与变形特性.

综上，水泥石受力及封隔能力方面的研究仍需深入.本文在前人井下组合体力学研究成果基础上进行改进，考虑水泥浆凝固过程对组合体位移分布的影响，并根据水泥石材料特性推导了水泥石塑性阶段本构方程，建立了水平井套管-水泥石-地层组合体弹塑性力学模型，并借助ANSYS数值模拟验证该模型准确度.随后深入分析水泥石封隔能力失效的两种基本形式，并实现了对水泥石封隔能力的预测.

1 套管-水泥石-地层组合体弹塑性力学模型

1.1 假设条件及物理模型

水平井钻井完毕后需要注水泥固井，此时水泥浆以流体的方式注入套管与地层间的环空中，随着水泥浆逐渐凝固，套管-水泥石-地层三者间应力相互影响，最终可视为一个整体.本文选择页岩气水平井为研究对象，根据其地质及施工条件，建立套管-水泥石-地层组合体物理模型，模型假设条件如下：

1) 各组分材料为理想弹塑性体，弹性阶段为线弹性材料，且均不考虑各向异性；

2) 水泥浆完全驱替钻井液，无泥饼影响；

3) 井眼轴向尺寸远大于径向尺寸，模型简化为平面应变模型；

4) 忽略温度的影响；

5) 水泥石凝固后胶结界面处位移连续.

页岩气水平井段一般沿着地层最小主应力方向钻进，井眼在垂向上受到上覆岩层压力，横向受到地层最大和最小主应力影响.故水平井段物理模型如图1所示，pH为上覆岩层压力，ph为最大水平主应力(下标H为上覆岩层，h为水平horizontal)，两者均为压应力，p为井筒内静液柱压力，r1,r2,r3,r4分别为套管内半径、水泥石内半径、地层内半径和地层外半径且r4≥10r3.

1.2 数学模型

根据应力叠加原理，将非均匀应力模型分解为均匀地应力下圆孔模型和均匀地应力下厚壁圆筒模型，pH和ph分解方式为

(1)

整个厚壁圆筒[14]的平衡方程为

(2)

式中，σr为径向应力，σθ为切向应力.此方程为欧拉二阶线性齐次微分方程，求得该方程通解，再结合根据厚壁圆筒边界条件，求得厚壁圆筒模型弹性阶段应力及位移分布：

(3)

式中：a为组合体中套管、水泥石或地层任一内半径；b为相对应的外半径；υ为相对应的泊松比；E为相对应的弹性模量.

关于无限大平面圆孔模型的推导，在弹塑性力学著作也有讲解，本文给出简要推导，假设该模型内应力函数Φ为

(4)

(5)

式中，θ表示与水平方向的夹角.叠加式(4)与式(5)，得到非均匀地应力下水泥石弹性阶段力学方程：

(6)

式中，ε0表示模型初始时刻所产生的变形.模型位移计算需减去ε0，这是由于实际情况下水泥浆注入井下环空时为流体，后为固体，故初始地层压力的存在并不会使固体状态的水泥石发生形变.即在水泥石凝固后，其内初始应力不为零，初始位移为零.故位移计算中减去初始位移才符合井下实际工况.

当组合体不发生塑性变形时，方程(6)可计算组合体弹性阶段的应力与应变大小.

塑性变形是当材料受力超过一定极限时产生不可恢复的变形.塑性变形阶段水泥石变形量较大，极易产生微环隙，研究水泥石封隔能力不能忽略水泥石塑性阶段的变形规律.而在水平井压裂过程中，套管内压不断升高，造成水泥石产生塑性屈服后，弹性阶段的力学方程不再适用于水泥石塑性区，故需建立塑性阶段的组合体力学模型.

平面应变状态下的米泽斯屈服条件为

将米泽斯屈服条件代入组合体力学平衡方程(2)，再根据塑性区边界条件可求得塑性区应力分布[14]：

(7)

式中p3指套管外壁处径向应力.

由于塑性变形受外力加载历史影响，仅仅求出塑性区应力分布并不足以计算水泥石塑性变形.本文根据前人对水泥材料弹塑性的实验研究结果[15-16]，选择幂次强化模型对水泥石塑性变形进行简化研究，如图2所示.

图2中σp,σs分别表示弹性阶段应力和塑性阶段应力.材料卸载服从弹性卸载定律，εp为残余应变.针对水泥石而言，在套管内压较小时，其应力小于σs，水泥石处于弹性变形阶段，本构方程为σ=Eε.当套管内压逐渐增大，水泥石应力大于σs后，进入塑性变形阶段，本构方程为σ=AεB.

该模型表达式为

(8)

将塑性区应力分布式(7)代入式(8)中得到塑性区域本构方程：

(9)

式中A，B均为根据实验所确定的常量.从前人的实验数据来看，在有围压的情况下，A一般大于20，B一般小于0.4.

2 水泥石封隔能力失效分析方法

根据文献[17-18]的研究，横向封隔能力失效的原因为：套管内压升高，水泥石受压变形，当水泥石变形量超过其极限伸长应变率时，水泥石内部产生微裂纹，油气水沿横向微裂纹进入组合体内，造成封隔能力失效.

纵向封隔能力失效的原因为：套管内压从高压开始降低，水泥石在高压状态时由于发生塑性变形，其部分变形不可恢复，套管内压降低后，可能会造成胶结界面分离从而引起水泥石纵向封隔失效.

横向封隔能力失效的判断适用第二强度理论，该理论认为材料断裂只与极限伸长线应变有关，与应力状态无关.判断条件为

ε1≤[ε].

(10)

结合第1节中组合体弹性阶段力学模型可求得横向封隔能力失效的判断准则：

(11)

式中：ε1表示任一点处应变;εr，εθ表示水泥石径向及切向应变.

纵向封隔能力失效适用第四强度理论的米泽斯屈服准则.水泥石的纵向封隔能力失效的判断表达式为

(12)

式中:σ表示米泽斯等效应力;σ1,2表示第一与第二主应力.

通过式(6)和式(12)两个判别式分别结合水泥石材料特性中的许用应变和屈服应力，可判断在不同井下工况下水泥石横向封隔能力和纵向封隔能力是否失效.

3 模型可靠性验证

本文研究内容主要为套管-水泥石-地层组合体弹塑性力学模型和水泥石封隔能力失效分析方法，对二者分别采用数值模拟对比和实验对比的方式，验证本文理论研究的可靠性.

选取延长地区页岩气延A井的参数，作为可靠性验证和实例分析中本文理论模型计算数据，如表1所示.

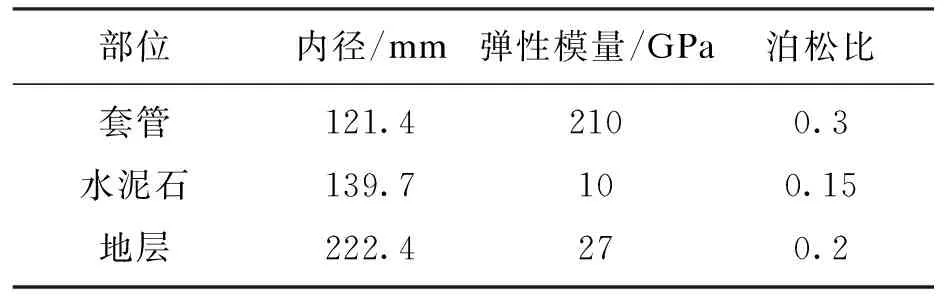
表1 延A井井眼参数Table 1 Wellbore parameters of Yan A well

3.1 组合体力学模型验证

在ANSYS数值模拟软件中根据表1所示参数建立井筒几何模型，几何模型设为三维模型，套管、水泥石、地层Z轴方向厚度均为10 mm，采用自由体网格划分方式对套管、水泥石、地层三者进行网格划分.网格划分结果如图3所示.

定义固井一界面与固井二界面接触类型时，分别建立套管、水泥石、地层的节点组件，固井两个界面均设为面面接触，材料单元间摩擦系数设为0.25，接触性质为弹性接触.套管内壁面施加表面应力70 MPa，组合体垂向方向施加表面应力18 MPa，组合体横向方向施加表面应力16 MPa.

模型求解后提取水泥石横向和垂向的等效应力分布，将其与相同条件下的本文理论模型计算结果进行对比，如图4，图5所示.

从图4，图5中可以看出，数值模拟结果与本文组合体力学模型计算结果基本一致，平均偏差不超过7%，充分验证了组合体力学模型的可靠性.

3.2 水泥石封隔能力失效分析方法验证

采用1993年Jackson固井水泥石封隔能力检测实验结果对本文理论模型进行验证.结合Jackson等对该种水泥的测量得到的应力-应变曲线(文献[10]图1)，可得到该种水泥石的屈服强度约为30 MPa，极限伸长率约为0.2%.

将其室内实验的参数代入本文模型编制的MATLAB程序中，求得在实验中水泥石内壁处等效应力与应变的变化过程，如图6所示.

从图6中也可以看出，套管内压升至69 MPa后水泥石等效应力为31.8 MPa，应变为0.17%.此时水泥石等效应力超过30 MPa屈服强度，应变未超过0.2%极限伸长率.根据本文水泥石封隔能力失效分析方法，此时气窜是由于水泥石产生塑性变形而产生微环隙导致的.该解释与实验中气窜后水泥石仍保持完整的实验现象一致.

对上述情况分析可以看出，本文水泥石封隔能力失效分析方法可以合理解释封隔能力失效的实验现象.

4 实例分析

4.1 水泥石弹性模量对封隔能力的影响

考察水泥石弹性模型对封隔能力的影响，对现场水泥种类和组分选择具有重要意义.根据本文模型，求解不同条件下的水泥石等效应力与应变.通过计算，当套管内压为80 MPa时，水泥石等效应力随水泥石弹性模量变化如图7所示.

由图7可知，同一弹性模量下，水泥石等效应力随水泥石直径增大而逐渐减小；同一水泥石直径下，水泥石等效应力随弹性模量的增大而增大.弹性模量大于12 GPa的水泥石等效应变曲线均出现突变点，证明其在套管内压80 MPa时出现了塑性变形.并随着弹性模量增大，其塑性区域不断增大.

从图7中发现，当弹性模量为4，8 GPa时，水泥石处于弹性变形阶段，需根据水泥石应变状态进一步判断其封隔能力是否失效，根据本文模型求得套管内压80 MPa时该两种水泥石应变，如图8所示.

由图8可知，同一弹性模量下，水泥石等效应变随直径增大而逐渐减小；同一水泥石直径下，弹性模量越小水泥石应变越大.在该计算条件下，弹性模量为4 GPa、直径在139～152 mm区间的水泥石应变已经超过0.2%，该区间水泥石内部变形超过材料极限拉伸极限，已经出现不可逆的微裂纹，可判断当套管内压为80 MPa时，弹性模量为4 GPa的水泥石封隔能力已失效.

同理，弹性模量为8 GPa的水泥石由于应变并未超过极限伸长率0.2%，判断当套管内压为80 MPa时，弹性模量为8 GPa的水泥石封隔能力未失效.

综上可知，在水泥石弹性模量参数选择中应综合考虑等效应力与应变程度.根据本文理论模型计算套管内压为80 MPa时等效应力和应变随水泥石弹性模量的变化曲线，如图9所示.

等效应力和应变随水泥石弹性模量的变化曲线也可称为水泥石封隔能力图版.因为从图中可预测水泥石封隔能力何时失效，当水泥石弹性模量为4 GPa时，水泥石等效应力36.6 MPa、应变0.24%，其应变超过极限伸长率，故水泥石发生纵向封隔能力失效.

从图9中可以看出，随着水泥石弹性模量增大，水泥石所受等效应力逐渐增大，应变逐渐减小.其中A区域水泥石等效应力未超过等效屈服应力，应变未超过极限伸长率，故此范围内水泥石封隔能力完好，即弹性模量为6～9.7 GPa的水泥石有利于保持水泥石封隔能力.

4.2 套管内压对封隔能力的影响

根据本文理论模型计算其水泥石内壁处等效应力与应变随套管内压变化曲线，如图10所示.

从图10可以看出，等效应力与应变均随套管内压增大而增大，且增长趋势都近似为直线.从4条曲线对比来看，两种水泥石在套管内压变化全过程中等效应力与应变均未超过极限值，故两种水泥石均可在套管内压变化全过程中保持封隔能力.

现场实际选择时，应以水泥石的屈服应力和极限伸长率为依据，结合封隔能力图版来选择水泥石最优配方.

5 结 论

1) 水泥石封隔能力失效形式主要分为横向封隔能力失效和纵向封隔能力失效，横向封隔能力失效主要由水泥石所受等效应力超过屈服强度引起，纵向封隔能力失效主要由水泥石应变超过极限伸长率引起.

2) 同一条件下，低弹性模量水泥石的等效应力小、应变大，适用于高压力地层；高弹性模量水泥石等效应力大、应变小，适用于低压力地层.

3) 水泥石弹性模量对封隔能力影响存在最优区间，根据水泥石封隔能力图版，在本文计算条件下水泥石弹性模量在6～9.7 GPa之间有利于保持水泥石封隔能力.