基于试题诊断的高三数学教学实践
2020-09-15王世朋
王世朋

高三二轮数学复习是以提升学生解题能力、完善学生思维品质为主要目的。如何使复习更精准,是高三教师必须思考的问题,也是有意义的研究课题。笔者基于课堂教学中的实践案例分析,强化试题诊断功能,借此提升复习的精准度。
一、基于试题诊断的案例分析
为了有效完善解析几何中直线与抛物线综合问题解题策略,笔者重点选择了合肥市2017年二模(文)第20题进行教学诊断与讲评后反思。
试题:已知抛物线E∶y2=2px(p>0)与圆
O∶x2+y2=8相交于A,B两点,且点A的横坐标为2,过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M。
求抛物线E的方程;
求点M到直线CD距离的最大值。
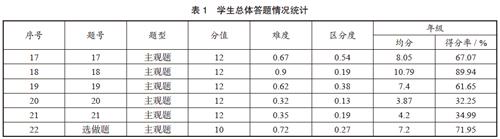
学生总体答题情况统计:
阅卷统计结果显示,本题实际得分明显低于其他解答题(见表1),说明学生答题障碍很大,值得去进行教学思考和研究。通过答题明细可以看出,绝大部分学生仅完成了第一问的解答。这里有意遴选了两位得分较高的学生答题原卷,不难看出这两位同学解题路径基本明确,运算求解能力仍需提升,尤其是对解题关键点的突破还要强化理解。
二、试题诊断基本路径分析
通过此问题的分析与解答,不难提取出以下基本知识点。如点与曲线方程关系、劣弧的概念、过圆上一点的切线方程求法、过抛物线上一点的切线方程求法、两直线的交点、点到直线距离、圆的方程和抛物线方程。作为一道题所涵盖的知识点已经足够多了,如果学生基本功不扎实,有知识混淆点或盲点,问题也就无法有效解答。通过以上知识点的梳理,我们可以很清楚地帮助学生梳理教材知识点,回顾知识发生、发展的过程,助力形成坚固的知识体系和脉络。
1.诊断基本解题方法
通过知识点的回顾,就需要我们提出解题的策略,尤其是可执行的具体方案。通过问题的条件分析,我们可以清晰地知道解题路径为:利用点坐标求抛物线方程求直线方程,并设C,D坐标
求出l1,l2方程求出点坐标计算点到直线距离转化为函数问题求解最值。为了解题的顺利进行,需要进一步明确方法求直线方程、求点坐标和函数最值。
2.诊断学生思维过程
通过解法的提出,在实际中需要执行运算,确保为下一步的执行提供准确、可靠的数据结果。通过答题过程就能有效监测一个学生的思维品质好坏,如动点P(x0,y0)作圆O的切线,切线方程的求法与表示,如果选择设点斜式切线方程,则要考虑斜率是否存在,如果能理解过圆上一点的切线方程一般形式,则解题步长就减少了很多。在C,D点坐标的设法上如果沿用椭圆常规设法,會给后面l1,l2写法带来不便,而选择抛物线上点的常用设法,会让后面M点坐标计算得到简便。在点M到直线CD距离最值求解上,本着函数思想为原则,点M坐标的简化就显得尤为重要。以上这些问题处理的策略,代表的是学生答题的数学思维水平高低,如果能有效选择形式,某种程度上可以反映学生的思维能力高低。
三、基于试题诊断的教学策略分析
解析几何模块的复习常被师生视为较难啃的“骨头”,选填注重“小灵活”,大题注重“大融合”。对于学生来说,需要积累有效的解题活动经验,提升解题素养。对于教师来说,复习中要强化训练的总结与整理,授之以渔是关键。
第一,厘清解题路径。从近年来的高考真题和地方模考试题中可以看出,解析几何题往往需要结合图形进行分析解答。教学中需要强化把文字条件和图形语言进行紧密联系,最终把问题放入图形中,充分发挥几何直观和数学抽象功能,找到明确可行的解题路径。
第二,攻克解题要点。有了路径的指引后,需要强化学生关键点的计算。本题解决的第一个关键点是直线方程的计算,实施运算中要考虑直线可以垂直于轴,避免设点斜式时出现不严谨的情况。本题解决的第二个计算要点是切线的计算,设,,切线:,代入得,由解得,方程为,同理
方程为。第三个解题要点是点坐标求解,联立,解得,又方程为,其中,满足,,联立方程得,则,∴M(x,y)满足,即点
为。最后一个运算要点是点到直线距离。点到直线:的距离关于单调减,故当且仅当时,。只有解题中准确把握了解题关键点,借以学生良好的数学运算和数据处理能力,问题才能真正地得到解决。
第三,聚焦解题思想。最终要解决的问题是最值问题,因为P(x0,y0)在动,所以要建立函数模型,又考虑到点在直线上或点圆上动,所以可以建立关于的一元函数模型,进一步由题知自变量。要得到x0∈[2,2]最终的函数表达式需要通过点
到直线距离公式获得,这就需要我们计算点坐标和直线方程,难点自然就是计算出l1,l2方程并联立才能得到点坐标,并选择用变量x0,y0来表示坐标最理想。
四、借助试题诊断提升复习精准性的几点思考
美国数学家哈尔莫斯说:“数学的真正组成部分应该是问题和解。”通过解题教学促进学生深度思考,积极体验问题解决的思维过程,反思建构问题解决的活动经验。笔者认为,通过试题诊断开展探究教学,助力复习精准性提升应落实好以下几个环节。
第一,对比答题情况,判断试题讲解的价值。提出问题有时比解决问题更有价值,尤其是紧张的高三二轮复习中,好的问题一定可以助力复习的效率提升。通过前面综合分析,为了复习解析几何中圆与直线、直线与抛物线相关位置关系运算的掌握情况,选择了一道知识点容量较大的综合题,通过问题答题的基本情况对比,可以诊断学生的基本数学素养,也能洞察学生的思维发展水平,实现试题的选拔功能。总之,问题选择要具有很强的导向性,研究的问题选择很有代表性,则复习的精准性就能有了一定的保障,复习效率也会有显著提升。
第二,对比得分情况,定位试题讲解程度。通过答题情况对比,尤其是得分情况对比,很容易诊断学生对问题的理解程度,有助于教师对学情的准确把握。基于得分情况的分析,能够进一步反映学生对知识的理解、问题解决程度的刻画,如果在实际教学中能对已选问题很好地进行解析和判断,能深入挖掘问题解决过程中所蕴含的知识、公式、原理与思想,势必也会提高复习质量,助力学生的个性化发展。
第三,对比不同答题方法,诊断学生思维品质。虽然我们用心选好了问题,也事先备好了所有可能的解题路径,如果问题和策略不适合学生已有的学情,结果也一定不会让我们满意,所以有效开展课堂探究,分析不同解法学生所燃放的思维品质是非常重要的举措。尤其是紧张的高三课堂学习,每一节课都很重要,如果教师能基于学情进行教学设计和诊断,凝练问题解决的基本途径,相信对学生走出题海战术,提升学科素养大有裨益,也会助力师生良好关系的建立,助力学生良好思维品质的养成。
第四,对比不同答题程度,诊断学生意志品质。作为高三二轮复习,我们更多的是为学生提供学习的载体和引领,让学生们在探究中体验和深化对知识的理解与方法的应用,更重要的是训练和培养学生解题的能力和经验。经验需要经常总结才有效,经常使用才有用,所以进行探究训练后的总结是为我们积累经验的必备步骤。通过对不同答题程度的评判,能有助于准确诊断学生的意志品质,估计学生的学科潜力,预判学生的学习能力。
高考试题具有八大功能:测评选拔功能、科研选题功能、命题示范功能、知识延展功能、思维训练功能、数学思想渗透功能、教学导向功能与德育渗透功能。作为一线教师来说,强化对试题功能性的针对性训练与指导,提升学生综合解题能力是关键。
本文系2019年安徽省教育信息技术研究课题“基于教育大数据的高中数学学情诊断与精准教学的行动研究”(课题编号:AH2019048)的阶段性成果。
(作者单位:安徽省合肥市第七中学)
责任编辑:李莎
lis@zgjszz.cn
