内曲线转子驱动径向柱塞数字泵柱塞组件运动学及动力学特性分析
2020-09-15曾亿山范一杰耿豪杰
曾亿山,张 强,胡 敏,2,范一杰,耿豪杰
(1.合肥工业大学机械工程学院,安徽合肥 230009;2.浙江大学流体动力与机电系统国家重点实验室,浙江杭州 310027)
引言
风能是一种清洁且无公害的可再生能源,是世界各国高度重视并发展的战略性产业之一,在能源、环境保护等方面具有重要的作用[1]。目前,对风能利用的主要形式是通过安装风力发电机组,将风能转化为电能[2],未来的风力发电机组中变速运行将取代恒速运行[3]。近年来,由于液压传动型风力发电机组的优势显著,液压技术在风力发电中的应用开始引起广泛研究[4]。在液压变速恒频风力发电机组中,液压泵作为能量收集与转换元件,起着重要作用。由于风的波动性与间歇性,风力机转速大小极不稳定,传统液压泵难以在随机低转速工况下连续长时间地可靠运行,并且流量输出也不恒定。因此,需要设计合适的数字液压泵来满足风力发电所特有的随机发生和低速大排量工况的需求,以保证可靠高效地吸收风能并将其转换为稳定的流量输出。多位学者已对数字泵进行了大量的研究。齐礼东等[5]研究了一种径向柱塞数字泵能够借助于高速电磁开关阀组的PWM控制或柱塞行程的有效控制来实现随机低转速驱动下的恒流量输出;张斌等[6]研制了一种多排数字轴向柱塞泵,通过调节对各个柱塞对应的进口开关阀和出口开关阀的工作顺序,来实现对流量控制;李林等[7]提出采用液控单向阀控制柱塞单元有效输出/输入实现轴向柱塞泵/马达配流及变量的配流机构。但是已有的数字泵都是偏心轮式结构,较难实现低速大排量。考虑到现有的内曲线马达具有良好的低速稳定性,易于达到低速大排量,因此提出设计一种内曲线转子驱动径向柱塞数字泵来满足风力发电的需求,与内曲线马达不同,内曲线转子驱动径向柱塞数字泵需要重点解决柱塞吸油时的低压回程问题,本研究重点在于转子内曲线和回程曲线的设计,以及对泵柱塞组件的运动学和动力学进行分析。
1 内曲线转子驱动径向柱塞数字泵的工作原理
图1是多作用内曲线径向柱塞泵的工作原理图。该液压泵采用的是转子导轨的结构形式,内曲线转子与主轴通过花键连接,在主轴转动时,随主轴一起转动。从图1可以看出,柱塞的滚柱夹在转子内曲线和回程曲线之间,在转子的外侧回程曲线的帮助下,柱塞很容易进行回程运动,从而解决了传统液压泵自吸能力不强的缺点。在主轴转动过程中,当柱塞位于吸油区时,柱塞在外侧的回程机构以及低压油的压力作用下,运动到离转子中心最近的位置,此时柱塞腔容积最大,完成一次吸油动作。接着随着主轴运动,带动内曲线转子进行转动,在转子曲线的作用下,柱塞开始向外运动,柱塞腔容积逐渐减小,并最终到达离转子中心最远处的位置,此时柱塞腔内的高压油液完全排出,从而完成一次排油动作。由于柱塞组件与转子导轨之间采用了滚柱接触,而且滚柱一方面在内曲线导轨上运动,另一方面又与柱塞形成了转动副,采用滚柱接触大大减小了摩擦力,提升了柱塞泵的性能和寿命。
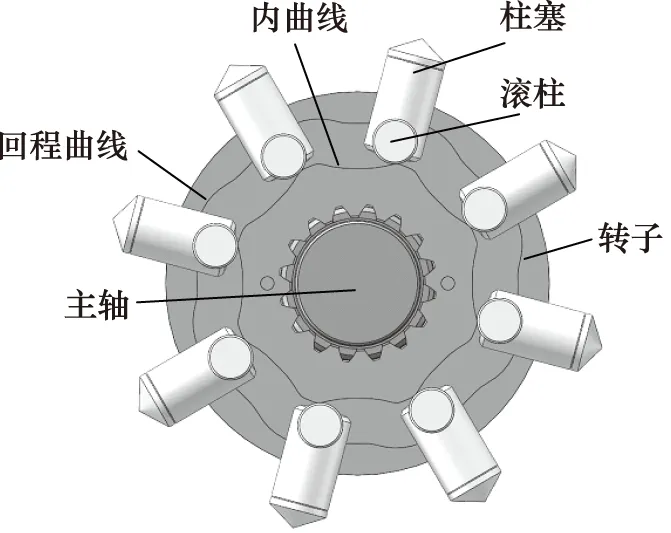
图1 多作用内曲线径向柱塞数字泵工作原理图
柱塞在单个吸排油区间内就可以完成1次完整的吸排油动作。而当转子含有x个这样的吸排油区时,内曲线转子每旋转1周,单个柱塞就可以完成x次吸排油的动作。如果再在泵轴向布置z个相同的转子柱塞组件结构,泵的排量将会呈z倍增加,这样不仅可以实现液压泵的低速大排量化,也可根据需要对径向柱塞泵排量加以控制。因此液压泵的排量可以用以下公式表示:
(1)
式中,d—— 柱塞直径
h—— 柱塞行程,即柱塞进行一次吸排油的运动位移
x—— 作用次数,即内曲线转子的凸起个数
y—— 柱塞个数
z—— 转子个数
从式(1)中可以看出,柱塞泵的排量与柱塞直径,柱塞行程,作用次数,柱塞个数,以及转子的个数这5个变量是成正比的。增大上式中5个变量的1个或几个变量即可增大泵的排量。
2 柱塞组件运动学和动力学分析
2.1 作用曲线设计与柱塞组件运动学分析
在已有的大部分内曲线马达中,定子曲线采用的是等加速运动曲线,简称等加速曲线[8]。等加速曲线具有较好的性能,可通过合理分配吸油区和排油区的幅角,得到性能良好的内曲线转子驱动径向柱塞泵。为了防止由于加速度的突变导致滚柱与导轨之间的接触应力值的突变,从而给导轨带来损坏,因此等加速曲线常常会设有零速区。径向柱塞泵的吸油区和排油区曲线中,都设有零速区、加速区、等速区和减速区[9]。
如图2所示,等加速曲线是由零速区、加速区、等速区、减速区组成的,若AB段是吸油区,BC段是排油区,则吸油区的幅角(ψm),ψm0,ψm1,ψm2,ψm3分别是吸油零速区、加速区、等速区、减速区。排油区的幅角为(ψn),ψn0,ψn1,ψn2,ψn3分别是排油零速区、加速区、等速区、减速区,吸油区和排油区的总幅角为ψz。将前人对径向柱塞泵定子曲线的幅角分配的研究结果[9]应用到转子内曲线上,则吸排油区域各个角度占比具体分配如表1所示。
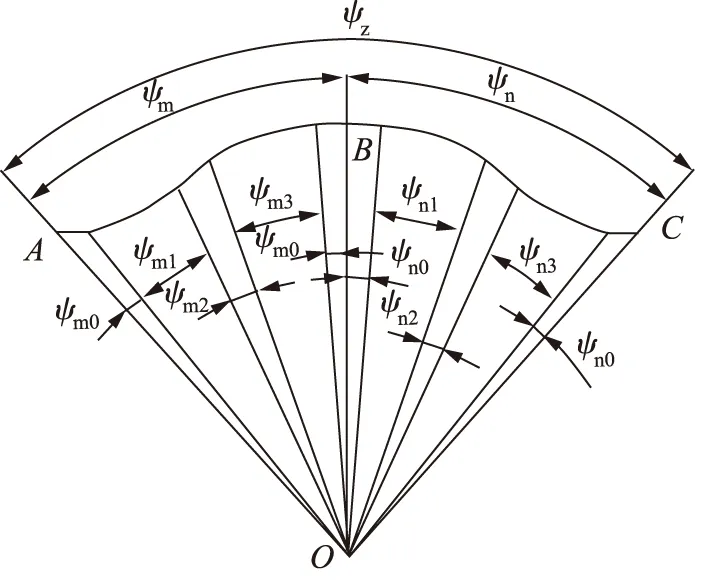
图2 等加速曲线幅角分配图
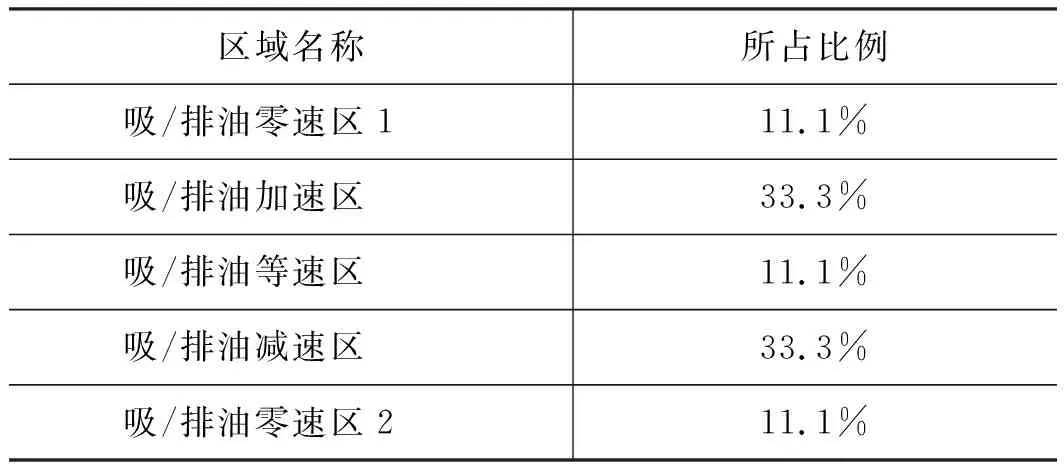
表1 吸/排油区域各个角度占比
内曲线转子径向柱塞泵的单个柱塞的运动规律可以等效为凸轮滚柱机构的运动来分析。如图3所示,弧AC段是内曲线转子导轨上的单个作用曲线,当内曲线转子顺时针旋转时,柱塞滚柱进入弧BA段运动时,柱塞组件在转子导轨的作用下向着缸体中心作回程运动,此时柱塞腔容积增大,液压油经过吸油窗口进入到柱塞腔内,完成吸油过程;柱塞滚柱在弧CB段运动时,柱塞组件背离缸体作径向运动,此时柱塞腔容积减小,迫使油液排出柱塞腔,完成排油过程。柱塞组件的运动取决于转子内曲线的形式,为了简化分析,可以用柱塞滚柱来代替柱塞组件的运动。如图4所示,A1B1C1是内曲线转子的一个作用曲线,A2B2C2是滚柱中心的运动轨迹。在一开始零速区为起始位置,滚柱中心距主轴中心的距离OA2是ρ0,在转子转动的过程中,滚柱中心距主轴中心的距离OO1是ρθ,当转子在dt时间内转动dθ的角度时,滚柱相对于转子从O1点运动到O2点,此时滚柱的径向位移为dρ,因此可算出滚柱的径向线速度vρ。

图3 单作用曲线柱塞运动示意图
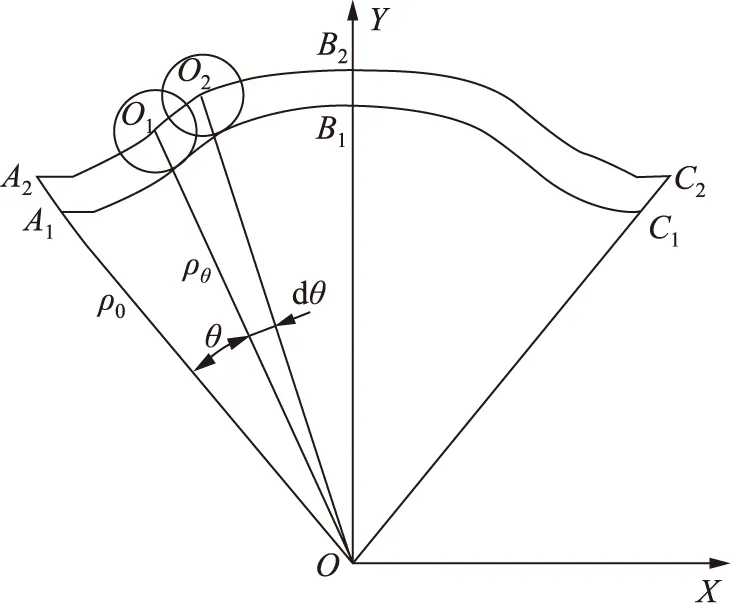
图4 柱塞滚柱运动简图
(2)
(3)
式中,vθ称为度速度[10],即滚柱在单位转动角度上的径向位移;ω为转子在泵轴带动下的角速度。
继续对径向线速度vρ进行角度的一阶微分,可得滚柱的度加速度aρ。
(4)
(5)
其中,aθ称为度加速度[10]。
在得出度速度和度加速度公式的前提下,对度加速度和度速度进行积分即可得出柱塞组件的运动规律。柱塞组件的度速度为:
(6)
柱塞滚柱在某个角度距离转子中心的距离为:
(7)
通过上述公式可以得到滚柱中心运动理论推导公式,接下来需要对转子内曲线和回程曲线进行理论推导。使用微元的思想[9],转子曲线是一个不规则的图形,柱塞滚柱和转子的位置关系是相切,由相切的几何特性,过曲线上该点做该点的法线方向的一条直线,滚柱最内侧的点,是滚柱与转子内曲线的接触点,而滚柱的最外围的点,则在接触点与圆心相连的直径之上,也是转子回程曲线上的点。由数学公式,在极坐标系下,曲线的极半径ρ(θ)与其导数ρ′(θ)之比等于极半径与曲线切线之夹角的正切,数学表达式如式(8)。由图5可知,α=ψ+θ,则曲线切线在M点的法线方向为过M点的水平线顺时针旋转了90°-ψ-θ,这样可以根据滚柱的直径确定内曲线和回程机构曲线上点的位置。
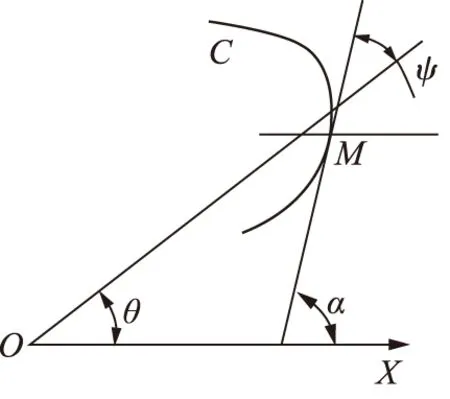
图5 回程曲线推导图
(8)
考虑到滚柱与导轨每点都需要保证相切,从而需要计算出滚柱中心运动曲线每点相对应的法线方向,并且需要计算出最小的曲率半径值。曲率半径公式如下:
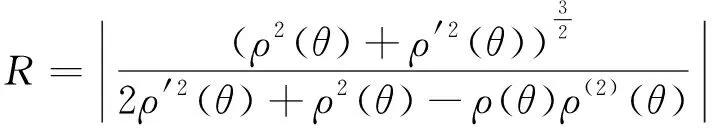
(9)
在利用已知的设计条件得到最小的曲率半径之后,滚柱的半径应小于等于滚柱中心运动曲线曲率半径值最小值,确定滚柱直径D之后,在MATLAB软件中进行绘制内曲线和回程曲线程序的编写,而内曲线的设计是基于极坐标系的,因此可以利用极坐标系与笛卡尔坐标系的转换公式得到:
x=ρ(θ)cos(θ)
(10)
y=ρ(θ)sin(θ)
(11)
接下来需要计算每个对应的内曲线和回程曲线上的点,可用以下公式得到:
xin=ρ(θ)cos(θ)∓0.5D×cos(90°-φ-θ)
(12)
yin=ρ(θ)cos(θ)±0.5D×cos(90°-φ-θ)
(13)
xout=ρ(θ)cos(θ)±0.5D×cos(90°-φ-θ)
(14)
yout=ρ(θ)cos(θ)∓0.5D×cos(90°-φ-θ)
(15)
式中,D—— 柱塞滚柱的直径
x—— 滚柱中心运动曲线的横坐标
y—— 滚柱中心运动曲线的纵坐标
xin—— 内曲线的横坐标
yin—— 内曲线的纵坐标
xout—— 回程曲线的横坐标
yout—— 回程曲线的纵坐标
按照这种方法,进行程序编制,考虑到后续需要对泵的排量进行控制,结合选用电磁阀的响应时间,将转子作用曲线设为8个。因此把整个转子曲线,看作是一个作用曲线绕原点,旋转复制8次得到。编程的主要参数如表2所示。
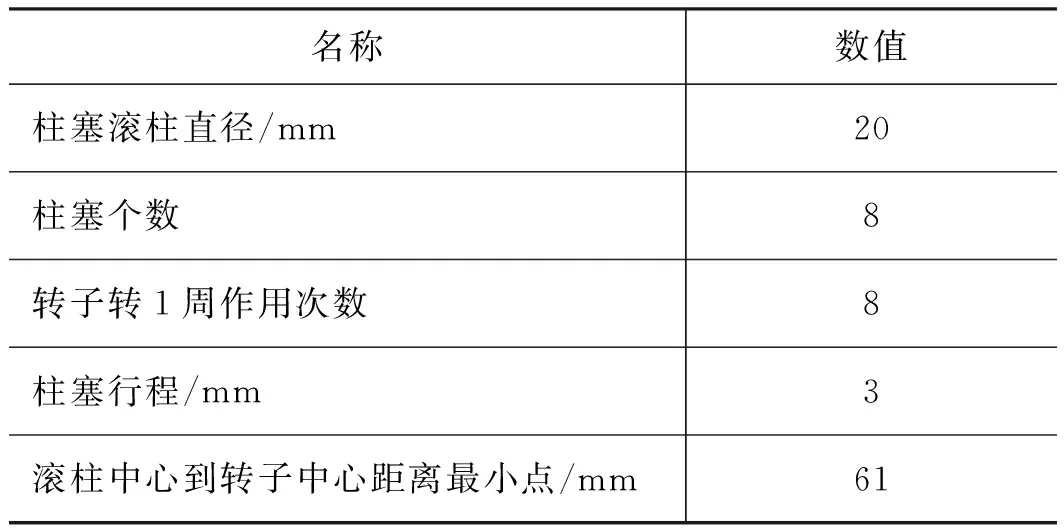
表2 编程参数
编完程序后运行可得到图6,点划线是转子内曲线,虚线是回程曲线,实线是柱塞滚柱中心的运动轨迹。

图6 MATLAB程序运行图
2.2 柱塞组件的动力学分析
如图7所示,内曲线转子驱动径向柱塞数字泵在运行时,柱塞和滚柱上的作用力有:柱塞底部的液压力Fp,柱塞滚柱组件运动时径向加速度产生的惯性力Fr,滚柱转动时受滚动摩擦力矩经过简化成滚柱中心的力F,柱塞与壳体柱塞孔之间的正压力N,柱塞在柱塞孔壁的摩擦力Ff,内曲线转子对滚柱的作用力Fn。

图7 柱塞滚柱受力分析简图
1) 柱塞底部的液压力p0
柱塞做径向往复运动,吸油时,在低压油液压力和转子回程机构的作用下做回程运动;排油时,柱塞底部受到高压油的液压力。液压力p0为:
(16)
式中,p为柱塞腔油液压力。
2) 柱塞滚柱组件的惯性力Fr
Fr=(m滚柱+m柱塞)ar
(17)
式中,m滚柱—— 滚柱质量
m柱塞—— 柱塞质量
ar—— 柱塞滚柱径向加速度
3) 滚柱转动时受滚动摩擦力矩[11]经过简化成滚柱中心的力F
(18)
式中,μ—— 滚动摩擦系数
R—— 滚柱半径
4) 柱塞与壳体柱塞孔之间的正压力N
转子转动时,转子对滚柱作用力的分力作用在柱塞上,最终柱塞和柱塞孔壁之间产生相互作用力。
5) 柱塞在柱塞孔壁的摩擦力Ff
Ff=f·N
(19)
式中,f为摩擦系数。
6) 内曲线转子对滚柱的作用力Fn
柱塞滚柱组件径向方向的力平衡方程为:
Fncosα+Fr+Ff-Fp=0
(20)
即:
(21)
其中,
(22)
由此可算得:
(23)
式中,α为压力角,压力角计算推导如图8所示。

图8 压力角计算推导图
压力角可通过以下方法来计算:过O1作OO2的垂线O1P,则O2P为滚柱径向位移dρ,O1P约为ρdθ,因此压力角[7]的正切值为:
(24)
3 柱塞滚柱组件的运动学与动力学仿真分析
3.1 径向柱塞泵虚拟样机建模

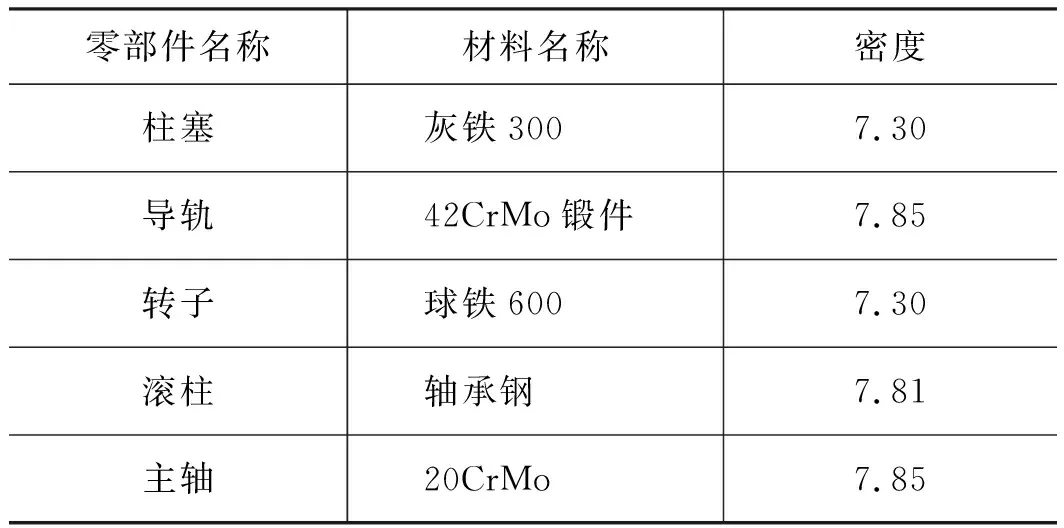
表3 径向柱塞泵主要零部件材料属性设置 g·cm-3
在对各个零部件赋予材料属性之后,就是对主要零部件创建约束关系,根据机械原理相关知识和径向柱塞泵的实际运动情况,添加的约束关系为:主轴-大地:旋转副;转子-主轴:固定副;回程导轨-转子:固定副;柱塞-滚柱:旋转副;柱塞-大地:平移副。
在对零部件之间添加约束后,滚柱与转子之间存在点线约束,对两者添加点线约束后,滚柱将按照设计的作用曲线运动。但是要想模拟滚柱运动的实际情况,需要在转子与滚柱之间添加contact接触副,使得滚柱与转子之间产生碰撞力。根据滚柱和转子的材料进行contact参数设置:材料的刚度设为100000 N/mm,金属材料的力指数一般取1.3~1.5,这里取1.5;阻尼一般取刚度的0.1%~1%,取值100 N·s/mm,穿透深度指的是材料之间的最多嵌入深度,一般取值0.1 mm。
内曲线转子驱动径向柱塞数字泵运动期间,进行吸排油动作时候,柱塞底部会受到液压油压力的作用。柱塞吸油时压力较低,排油时压力较高。因此,按照吸油压力1 MPa和排油压力20 MPa在ADAMS中可通过函数表达式来定义柱塞受到的液压力大小。根据径向柱塞泵在工作时受到的液压油压力,使用样条曲线函数AKISPL添加的液压力曲线如图9所示(以泵轴转速为30 r/min为例)。
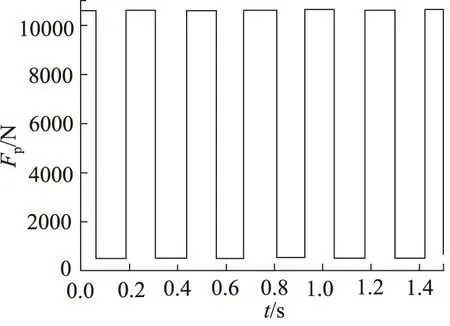
图9 液压力样条曲线图
ADAMS中的动力学模型如图10所示。

图10 径向柱塞泵主要零部件动力学模型图
3.2 仿真结果分析
仿真完成之后,对仿真结果进行分析。
1) 柱塞滚柱的运动学分析
在图11~图13柱塞滚柱质心的速度变化曲线图中,实线是滚柱与转子设置contact接触时,滚柱的速度变化曲线;虚线是滚柱与转子设置点线接触时,滚柱质心的速度变化曲线。滚柱与转子设置点线接触是比较理想的情况,滚柱与转子的接触点和转子曲线始终不脱离,因此速度曲线有着预期的零速区、加速区、等速区、减速区,其中等速区速度有不稳定的情况,原因是MATLAB导出点坐标到三维建模软件中,会出现某些点不连续的情况,整个曲线速度最大值为35 mm/s,基本无速度突变。但是泵在实际运动过程中,在滚柱直径取值较小时,即配合间隙较大时,速度在等速区会有突变,突变峰值能达到在46 mm/s,且速度波动变化较频繁。当配合间隙值取最小公差时,即滚柱直径取19.94 mm时,速度曲线波动变小,速度突变峰值也减小,整体曲线性能变好,和理想速度曲线基本重合。由于滚柱直径略小于内曲线和回程曲线的间距,速度值不会完全按照设计的内曲线来变化,这也反映了滚柱的真实运动状况,滚柱运动较平稳。因此滚柱直径可按照最小配合公差取值19.94 mm。
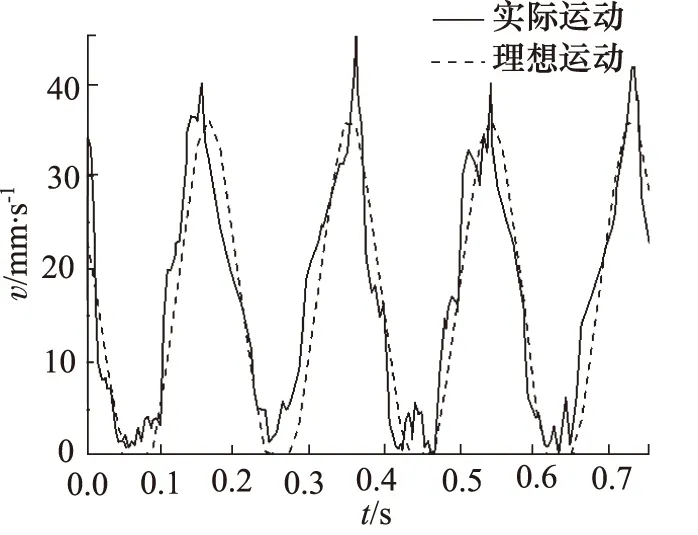
图11 φ19.85滚柱质心速度变化图

图12 φ19.89滚柱质心速度变化图
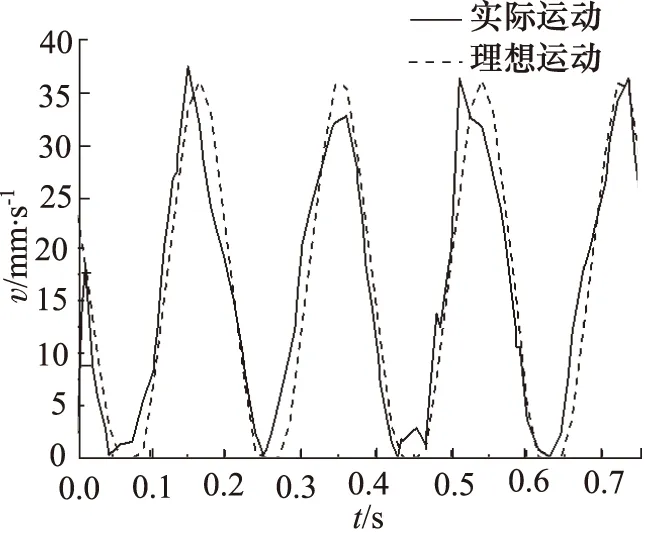
图13 φ19.94滚柱质心速度变化图
图14是在转子转1个作用曲线过程中,φ19.94滚柱运动位移曲线图。实线是滚柱与转子之间设置点线接触时,即理想情况下的滚柱运动位移曲线;虚线是滚柱与转子之间设置contact时滚柱的运动位移曲线,柱塞滚柱在转子内曲线和回程曲线的作用下往复运动。实线光滑且连续,无速度突变区,符合内曲线设计目标。虚线和实线形状相似,柱塞滚柱实际运动时平稳,无刚性冲击,实际运行情况较好。
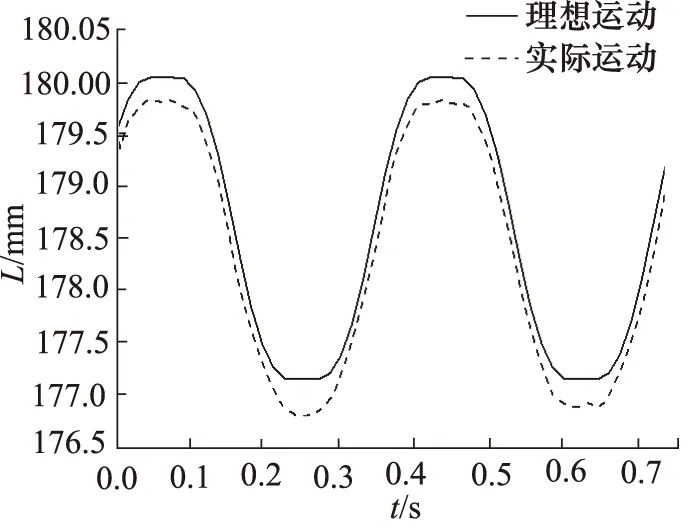
图14 φ19.94滚柱的运动位移曲线图
2) 柱塞滚柱的动力学分析
图15是泵在运行过程中,在柱塞底部添加液压力时,滚柱与转子的接触力变化曲线。高压油作用下,滚柱与转子的接触力规律性地波动,整体的接触力数值上几乎相等。低压油作用下的接触力波幅度比高压油作用下小很多,接触力值在滚柱运动过程中也近似相等。
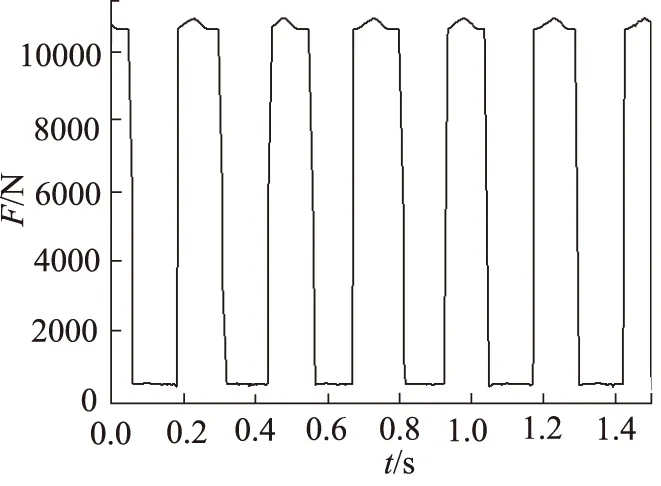
图15 液压力作用下滚柱与转子的接触力曲线图
图16是在不同转速情况下,在柱塞底部添加液压力时,滚柱与转子的接触力变化曲线。虚线是转子转速为10 r/min时,滚柱与转子接触力变化曲线,实线是转子转速为30 r/min时,滚柱与转子接触力变化曲线。从图中可以看出,滚柱与转子的接触力主要与液压力有关,接触力周期性变化,呈锯齿状在一个平衡值处上下波动,整体的接触力数值上几乎相等。转子转速在10 r/min和30 r/min时,接触力曲线波动相似,受力情况相近。由于径向柱塞泵用于液压风力发电机组,风力机转速一般为10~31 r/min,而转子与滚柱的接触力在低速情况下有良好的稳定性,力数值变化有规律性,性能较好。
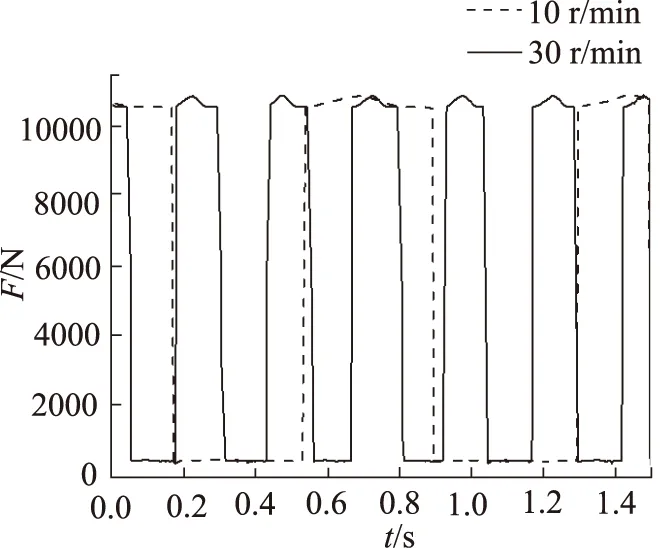
图16 不同转速下滚柱与转子的接触力曲线图
4 结论
提出了一种内曲线转子驱动径向柱塞数字泵,对其进行内曲线和回程曲线的设计,并进行柱塞组件的运动学及动力学特性分析,这种泵有以下优点:
(1) 在风力发电领域有较好的应用前景,在内曲线转子转动1周的过程中,泵可进行多次吸油和排油,解决了传统液压泵在低速情况下难以实现大排量化的缺点;
(2) 内曲线转子驱动径向柱塞数字泵采用滚柱凸轮的接触形式,将柱塞与转子之间的滑动摩擦变为滚动摩擦,减小了摩擦力,提升了柱塞泵的性能和寿命;
(3) 滚柱在转子内曲线和回程曲线的作用下来回运动,在分析比较不同滚柱直径的运动学特性之后,确定合适的滚柱直径,仿真结果表明滚柱运动时无较大的冲击,回程曲线能较好地帮助柱塞完成回程动作,柱塞滚柱运动连续平稳,受力均匀有周期性。在风力低速驱动的条件下,具有良好的运动学和动力学稳定性。
