基于模型的Meta分析方法在抗糖尿病药疗效评价中的应用现状Δ

闫开成，蔡 芸，王 睿

(中国人民解放军总医院医疗保障中心药剂科，北京 100853)

2017年，全世界糖尿病患者数已超4亿例，预测到2045年将达到6亿例[1]。90%的糖尿病患者为2型糖尿病患者。2型糖尿病是由于胰岛素分泌和敏感性降低，引起的以慢性高血糖为特征的代谢性疾病。如果患者长期处于高血糖状态，会导致动脉粥样硬化性心血管疾病和微血管病变，如糖尿病肾病和糖尿病视网膜病变。因此，平稳有效地控制血糖至关重要。虽然有倡导饮食疗法和体育锻炼等方式作为糖尿病的一线治疗，但基本药物疗法仍是控制血糖的最有效方法[2]。抗糖尿病药种类繁多，目前美国糖尿病协会推荐的临床常用抗糖尿病药有7大类，包括二甲双胍、二肽基肽酶4(dipeptidyl peptidase 4，DPP-4)抑制剂、胰高血糖素样肽-1(glucagon-like peptide-1，GLP-1)受体激动剂、钠-葡萄糖协同转运蛋白2(sodium-dependent glucose transporters 2，SGLT-2)抑制剂、噻唑烷二酮类药物、磺酰脲类药物和胰岛素[3]。上述各类抗糖尿病药中已有多个品种为临床用药，还有很多为正在研发的新药，因此，在临床上如何针对患者个体化地选择抗糖尿病药显得尤为重要。以患者为中心的疗法，首先要考虑选取药物的功效或联合用药的种类；其次要掌握药品不良反应，如低血糖风险和体重的变化；再者需参考药物费用和患者的选择权。

目前，临床上对单个抗糖尿病药的疗效评价，主要是基于对药物治疗终点的评估，如糖化血红蛋白水平、体重改变情况和药物的低血糖风险[4]。传统的随机对照试验可有效评估不同抗糖尿病药的疗效[5]；但很难对所有的治疗方案一一进行对比，且临床试验的实施难度较大，成本高昂。网状荟萃分析(Meta分析)可以对多个研究效应值进行合并，并报告其效应值的可信区间，以图表的形式呈现分析结果[6]；但其仅适用于现已存在的随机对照试验，并且所分析药物的观察期和剂量限于特定范围，而且很少评估协变量对疗效的影响，这样会使得疗效尺度不够精确，混杂因素增多。基于模型的Meta分析(mode-based meta-analysisi，MBMA)是一种先进的定量分析技术，其可以有效弥补上述不足，即使在缺乏随机对照试验时也具有间接的比较能力，依据每个抗糖尿病药的治疗终点进行广泛分析和适当调整，对治疗持续时间、血红蛋白基线水平、体重基线水平、背景治疗和剂量方案等加以整合，达到对多种抗糖尿病药的综合评估[7]。因此，MBMA较传统的Meta分析更具灵活性，并有望提供更多信息。现将MBMA的基本原理及其在抗糖尿病药临床评价领域的应用进行综述。

1 MBMA的研究原理

MBMA是建立在传统的Meta分析及Meta回归基础上，加入参数模型来描述剂量效应、时间效应关系等[8]。通过搜集大量临床研究数据，基于主要自变量，建立描述数据特征的数学模型。在此基础上，添加协变量以分析其对因变量的影响，并从统计角度考虑随机效应以形成最终模型[9]，定量剂量与药效、时间与药效的关系。应用该模型，改变试验条件进行模拟研究，可比较不同剂量或时间下，药物的效应变化情况。MBMA可以整合不同药物持续时间和不同采样点的试验数据，这就降低了研究数据的纳入和排除标准的限制，以便全面准确地分析更多的相关数据，间接地评估多种抗糖尿病药的不同功效，从而指导临床用药。

MBMA属于定量药理学范畴，正成为系统评价药物有效性和安全性的重要工具。构建模型后，可以引入协变量来对抗糖尿病药进行总体评估，如年龄、性别、体重指数、病程和剂型等，这样可以筛查关键的药效影响因素。同时，MBMA的分析结果可以用来模拟和预测，更好地为个体化治疗提供依据，也可为新药的研制提供验证模型[10]。因此，MBMA在研究药物的治疗效果时显得更灵活，可提供更多的反馈信息，便于临床医师参考。

2 MBMA的研究流程

2.1 数据分析

根据要研究的抗糖尿病药，制定有效的检索策略和文献的纳入、排除标准，并由2名研究人员提取、比较和检查数据。最终从纳入的文献中提取所需信息，包含受试者基础信息(性别、年龄和体重等)、给药方案(给药种类、途径和疗程)、临床检验(血糖监测、血生化和血尿常规)、临床试验方案(随机、对照和盲法)以及其他影响药物的因素，并对以上数据进行严格的质量控制。

2.2 模型构建

MBMA主要由统计学模型和药效学(pharmacodynamics，PD)模型构成[11]。PD模型用于描述药物作用强度与药物剂量或浓度之间的关系，反映PD特征。统计学模型用于描述各种变异，例如试验间变异和残差变异，反映了药效的变异程度[12]。以药效评价为例，MBMA的经典模型如下[13]：

(1)

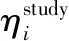
指数型：

(2)

加和型：

(3)

公式(2)和(3)中，Ei为第i个研究的药效经典值，η1,i和η2,i分别为PD参数Emax和ED50的试验间变异，如果符合以0为中心的对数正态分布，则将其以指数型的形式添加到对应模型中；如果符合以0为中心的常数正态分布，则以加和型的形式添加到相应模型中。究竟这种变异符合哪种分布形式，可以通过模型的目标函数值来判断，目标函数的值越小，则拟合度越好。

可以通过以下形式将协变量对模型参数的影响引入模型中：

Pi=Ptypical+θ·covariate1

(4)

公式(4)中，Pi为第i个研究的PD参数，Ptypical为PD参数经典值，θ为协变量对PD参数的影响。如果添加的协变量极大地改变了PD参数，则表明协变量对模型参数有重大影响，应将其保留在模型中。

2.3 模型评价

对最终模型的评价方法与群体药动学(pharmacokinetics，PK)评价方法类似，可通过基础拟合优度图(basic goodness-of-fit plots，GOF)进行诊断评价[14]。其中，PD模型的验证一般有内部验证和外部验证2种方法[15]。(1)内部验证可采用基于模拟的可视化预测检验(visual predictive check，VPC)和随机自举模拟(Bootstrap)方法，对模型的稳健性和预测力进行评估，对参数估计值的准确性等进行验证。VPC法是对最终的模型进行(一般≥1 000次)模拟，得到预测的置信区间，根据模拟结果与观察的结果作图比较。Bootstrap法对现有数据进行随机抽样，形成一般≥500个的新数据集，并对新数据集参数进行估计，通过与实测值估计比较，验证模型[16]。(2)外部验证则需要满足纳入条件的其他临床研究数据，通过比较最终模型的预测值和测量值来评估模型的合理性。最终的模型反映了药物疗效的分布特征和变异情况，通过蒙特卡罗模拟方法[17]，根据PD参数和变异参数的分布，随机选取数值并计算药效值。

2.4 应用软件

目前，常用的文献管理软件为EndNote和Mendeley软件，利用Review Manager软件对所提取的数据进行规范化整理，使其符合NONMEM软件对数据格式的要求，并实现数据可视化。NONMEM软件是专门用于非线性混合效应模型拟合的软件，已广泛用于建立群体PK和群体PD模型，并且是用于定量药理学研究的专业工具软件[18]。

3 MBMA在抗糖尿病药疗效评价中的应用

抗糖尿病药种类繁多，个性化用药要求有针对性和时效性，而联合用药在临床也很常见，这就更需要有一个实用的模型来有效对比，合理选择联合用药方案。基于经典的MBMA，根据考察抗糖尿病药疗效指标的不同，有针对性地选取变异模型显得更便捷。一般而言，血糖控制水平、体重改变和低血糖风险是选取抗糖尿病药参照的重要因素，在药物疗效对比上还需考虑空腹血糖和糖化血红蛋白的基线水平、治疗间期和药物剂量等[19]。

3.1 单个药物与安慰剂的比较

药物临床研究常规选用与安慰剂效应的比较，观察药物的净效益和药物的剂量选择，以及一些未被发现的临床效果。他司鲁泰是一种GLP-1受体激动剂，降糖作用显著，由于临床推荐剂量(10或20 mg)会引起严重的胃肠道不耐受和过敏反应，所以未在我国上市时就于2010年被停止使用[20]。为了重新考究他司鲁泰的药用价值和潜力，Li等[21]搜集了以往临床试验数据，通过构建空腹血糖和糖化血红蛋白随药物剂量变化关系的PD模型，来比较安慰剂与他司鲁泰10、20 mg用量的疗效，以期通过该定量模型进一步了解他司鲁泰的净效益和更多的降血糖信息。结果发现，与安慰剂比较，他司鲁泰对2型糖尿病有明确疗效，3.5个月即可达到平稳的降糖作用；他司鲁泰10 mg与20 mg两种剂量比较，在以糖化血红蛋白为治疗终点的模型中无显著差别，在以空腹血糖为治疗终点的模型中他司鲁泰20 mg比10 mg略显有效，但他司鲁泰20 mg产生的不良反应明显高于他司鲁泰10 mg和安慰剂；通过MBMA来研究抗糖尿病药的空腹血糖和空腹血糖与糖化血红蛋白的关系，可用于以后的研究设计，包括优化治疗剂量和持续时间。虽然他司鲁泰在临床上已被停止使用，但通过构建有效的MBMA来整合临床试验数据，能够全面考察药物的用量、疗效、评价指标和安全性等各方面信息，对单个药物的充分了解有助于未来对该药的再次利用。

3.2 2种以上抗糖尿病药的疗效比较

由于抗糖尿病药种类繁多，各类药物优劣势不同，临床研究很难对每种药物都一一对比。MBMA有效地解决了上述难题，通过构建模型把各类药物纳入研究，针对患者的不同情况合理选择用药。

DPP-4抑制剂是一类相对较新的治疗2型糖尿病的口服抗糖尿病药，由于其临床疗效稳定、方便安全和副作用较小，在临床上逐渐成为常规用药。Gross等[22]运用MBMA对两种DPP-4抑制剂(经典药物西格列汀与新药利拉利汀)的疗效进行了比较，用蒙特卡洛模型拟合所收集的数据，得到了糖化血红蛋白在给药时间、剂量、洗脱期间和给药前糖化血红蛋白水平方面的药效方程。建立PK模型后，将其用于模拟2型糖尿病患者糖化血红蛋白含量为8%时西格列汀与利拉利汀的治疗效果。结果表明，最大剂量西格列汀(100 mg)与利拉利汀5 mg的治疗效果无显着差异。在这种情况下，药物选择需要基于患者的其他临床特征。例如，西格列汀的主要排泄方式为经肾脏排泄，而利拉利汀的主要经胆汁和肠道排泄。对于肾损伤的糖尿病患者，可以选择同等剂量的利拉利汀，就可以达到相同水平的降血糖作用。

PK/PD模型整合了药物剂量、药物浓度、生物标志物和结果效应的信息，这样的综合模型可用于模拟前瞻性研究、考察实验设计和解释个体间变化等。Gibbs等[23]运用基于PK/PD模型的Meta分析，度量了四种DPP-4抑制剂(阿格列汀、沙格列汀、西他列汀和维达列汀)的有效浓度，描绘了上述四种DPP-4抑制剂与糖化血红蛋白反应的关系，评估了协变量对糖化血红蛋白的影响，分别得出了上述四种药物的最佳剂量、治疗间期和适用的患者人群。例如，在每种DPP-4抑制剂的选定剂量下，80%以上的抑制时间百分比是可变的，从沙格列汀的40%到西他列汀的100%，而低剂量DPP-4的抑制值与66%～80%的范围更为一致。该研究通过MBMA，全方位地比较了同类的四种不同抗糖尿病药，为临床医师个体化用药时能够合理选择药品提供了数据支持，避免了经验性治疗的盲点。

Maloney等[24]对治疗2型糖尿病的常规6大类24种抗糖尿病药进行了全面的分析比较，运用MBMA，弥补了普通Meta分析难以解决的问题，如试验间的糖化血红蛋白标准基线的不同、糖化血红蛋白观察时间的不同、治疗间期的不同和药物剂量的不同，通过这样的有效模型，明确了抗糖尿病药类别间和类别内的差异。比如，通过对比发现，控制血糖能力最强的是GLP-1受体激动剂，最弱的是DPP-4抑制剂，但GLP-1受体激动剂又最易导致患者体重降低；磺酰脲类药物更容易导致患者低血糖风险和体重的增加。这样的研究可以使临床医师和患者更容易了解抗糖尿病药的相似和不同，有针对性地选择最佳药物及联合用药方案。

3.3 抗糖尿病药联合用药方案的比较

国际上大多把二甲双胍作为2型糖尿病患者的一线单药治疗方案，但二甲双胍长期治疗后可能发生继发性失败，当治疗失败时，推荐二甲双胍与其他抗糖尿病药的二联疗法。DPP-4抑制剂、GLP-1受体激动剂和SGLT-2抑制剂各自有新的作用靶点，并且很少引起体重增加和低血糖风险等副作用。但由于随机对照试验和传统Meta分析很少直接比较联合用药的有效性，因此，目前缺乏共识。Inoue等[25]运用群体PD模型对不同组合的联合用药进行了比较，并且囊括了有效的剂量反应数据，允许定量的剂量反应关系和时间进程的影响。该研究定量分析了DPP-4抑制剂、GLP-1受体激动剂和SGLT-2抑制剂对2型糖尿病患者空腹血糖和糖化血红蛋白的作用效果，评价与二甲双胍联合的最优方案。MBMA结果显示，二甲双胍联合DPP-4抑制剂或者SGLT-2抑制剂的降糖效果相似，但长效的GLP-1受体激动剂与二甲双胍联合用药展示出比其他两类更好的效果。糖尿病治疗后期大多需要联合用药，才能使血糖保持平稳水平，通过MBMA方法模拟预测不同药物联合作用效果，能够根据患者病情发展需要快速有效地选择联合用药方案。

4 结论

MBMA基于已有的临床研究，通过搜集整理相关的试验数据，根据研究的侧重点建立相应的PK模型和统计学模型，引入协变量的方法合并足量的临床数据，来对不同药物进行对比。MBMA还可以为临床方案的制定、药物开发决策和药物疗效指标比较等提供许多有价值的信息。由于抗糖尿病药种类繁多，相关临床试验对药物的治疗终点、剂量选择和治疗周期不统一等，给临床上针对不同患者实施个体化用药带来难度。MBMA就为临床医师提供了一个可靠且有效的方法，可基于客观数据建立模型评估药物疗效和安全性，从而做出合理选择。

当然MBMA的应用也存在一定的限制。一是MBMA建模分析计算对研究人员的专业技能要求较高，需要具有定量药理学或统计学专业背景。因此，国内外对MBMA的研究应用仍然偏少。二是由于实际情况对数据可访性的限制，MBMA存在选择性偏移的关键缺陷，这可能导致数据的不完整和偏差性数据的混入。因此，在分析规划、模型开发、模型评估、灵敏度分析和基于模型的模拟方面，要主动评估，从源头上减轻结论可能出现的风险。三是针对患者个体的PD分析，MBMA在评估协变量的影响时还很难涵盖所有数据，难以达到因人而异。但随着从临床实践环境中获得越来越多的临床试验数据和真实世界的数据，MBMA将在药物临床评价领域起到更加重要的作用。