混合溶媒异丙醇-乙二醇二甲醚精馏分离研究
2020-09-15黄嘉琳许松林杨义龙
黄嘉琳,许松林,杨义龙
(1. 天津大学 化工学院,天津 300350;2. 安徽贝克联合制药股份有限公司,安徽 合肥 236604)
异丙醇与乙二醇二甲醚均为重要的化工原料,作为溶剂或萃取剂等被广泛应用于石油化工、制药等领域。异丙醇作为石油燃料添加剂能有效防止化油器在寒冷条件下结冰,还可作为原料制取汽油添加剂、采油驱油剂,同时,石油也可用异丙醇进行萃取或提纯。乙二醇二甲醚可作为柴油添加剂,能有效降低烟度和改善发火性[1-2]。
在利托那韦与洛匹那韦中间体合成和分离过程中,先后加入了异丙醇与乙二醇二甲醚,因此产生了大量的异丙醇与乙二醇二甲醚混合溶液,基于实际工业经济与环保的要求,需要对异丙醇与乙二醇二甲醚混合溶液进行分离,从而将异丙醇与乙二醇二甲醚回收再利用。但在常压下,异丙醇与乙二醇二甲醚的沸点相差不到2.0 ℃,采用常压精馏工艺很难将异丙醇与乙二醇二甲醚混合溶液进行有效分离。加压精馏分离工艺适用于该混合溶液的分离,且加压精馏只需要在一个精馏塔中完成分离,与传统双塔萃取精馏操作相比减少了设备费用及能耗,避免了外加组分对产品纯度的影响及对外加组分再回收的问题[3-4]。目前国内外对加压精馏分离异丙醇与乙二醇二甲醚混合溶液的研究甚少。
本工作利用异丙醇和乙二醇二甲醚两组分的沸点随操作压力变化不同的特性,采用加压精馏工艺对异丙醇与乙二醇二甲醚混合溶液进行分离,根据不同压力下异丙醇和乙二醇二甲醚二元体系的汽液平衡关系分析压力对体系相对挥发度的影响,并进一步说明加压精馏工艺的可行性。
1 热力学模型的选择
化工热力学以化学热力学和工程热力学为基础,主要任务包括平衡研究和过程热力学分析,它是化工过程开发、研究和设计的理论基础[5-6],常见的热力学模型有Wilson模型、NRTL模型、UNIQUAC模型、UNIFAC模型等[7-10]。
异丙醇分子中含有羟基,乙二醇二甲醚分子中含有醚键,二者分子之间存在一定的交互作用,因此混合溶液为非理想体系。本工作采用NRTL模型作为热力学计算的基础[11-13],在异丙醇与乙二醇二甲醚二元体系研究过程中,采用NRTL模型计算液相活度系数的非理想特性,气相按理想气体特性处理[10]。
NRTL模型的有序双液方程由Renon和Prausnitz在局部组成概念与双流理论的基础上提出[14],NRTL热力学模型方程见式(1)。

式中,Gij= exp(-αijτij),为溶液的相互作用能;αij和bij为二元相互作用参数,αij=αji;τij=aij+bij/T,为作用能参数;T为实验温度,K;xi为组分i的液相摩尔分数;γi为组分i的活度系数;i,j,k分别代表不同的组分。异丙醇与乙二醇二甲醚的二元相互作用参数见表 1[15]。

表1 NRTL方程二元相互作用参数Table 1 Binary interaction parameters of NRTL equation
2 结果与讨论
2.1 操作压力的影响
常压下,异丙醇的沸点为82.4 ℃,乙二醇二甲醚的沸点为84.0 ℃,两组分的沸点相差不到2.0℃,因此很难采用常压精馏工艺进行分离。异丙醇和乙二醇二甲醚的沸点均会随操作压力的变化而变化,两种组分沸点与操作压力的关系见式(2)和式(3)。

式中,T为温度,K;p为操作压力,Pa。对于非共沸二元混合物系,当两组分的沸点差大于10.0℃时可以采用精馏工艺将混合物进行有效分离,由式(2)和式(3)计算可得异丙醇与乙二醇二甲醚不同压力下的沸点差,结果见表2。

表2 不同压力下异丙醇与乙二醇二甲醚的沸点差Table 2 The difference in boiling point between isopropanol(IPA)-ethylene glycol dimethyl ether(DMEN) under different pressure conditions
由表2可知,当压力大于等于4.05×105Pa时,两种物质的沸点差大于10.0 ℃,但因一般采用低压饱和蒸汽(温度约为160.0 ℃)作为精馏塔再沸器的热源,综合考虑精馏塔再沸器饱和蒸汽的传热温差等实际问题,选择5.07×105Pa作为分离异丙醇与乙二醇二甲醚混合溶液的操作压力,并对该操作压力下异丙醇与乙二醇二甲醚混合溶液的实际分离情况进行进一步的分析。
2.2 二元组分气液平衡关系及相对挥发度的分析
对于异丙醇与乙二醇二甲醚混合体系,液相混合物为非理想溶液,气相为理想状态,则汽液平衡关系为[10]:

式中,p为总压;pi和yi分别为物质i的气相分压和摩尔分数;为物质的饱和蒸气压;xi为物质i的液相摩尔分数。
采用NRTL热力学模型来描述异丙醇与乙二醇二甲醚混合溶液的非理想性,即任意组分的活度系数由式(1)计算得到,不同组分的饱和蒸气压由式(2)和式(3)计算得到,最后通过式(4)计算得到1.01×105Pa和5.07×105Pa下异丙醇和乙二醇二甲醚二元组分的气液平衡相图,结果见图1和图2。
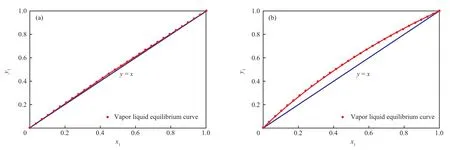
图1 1.01×105 Pa(a)和5.07×105 Pa(b)下异丙醇和乙二醇二甲醚的气液平衡相图Fig.1 Diagram of IPA-DMENsystem at 1.01×105 Pa(a) and 5.07×105 Pa(b).

图2 1.01×105 Pa(a)和5.07×105 Pa(b)下异丙醇和乙二醇二甲醚的T-x1(y1)相图Fig.2 T-x1( y1) diagram for IPA-DMEN system at 1.01×105 Pa(a) and 5.07×105 Pa(b).
由图1a和图2a可知,常压下异丙醇与乙二醇二甲醚的气液平衡曲线几乎与对角线重合,不同温度下气相线与液相线两条曲线几乎重合在一起,因此精馏分离即使在非常大的理论塔板数下,也难以取得较好的分离效果。由图1b和图2b可知,当操作压力为5.07×105Pa时,异丙醇与乙二醇二甲醚的气液平衡曲线明显偏离了对角线,不同温度下气相线与液相线明显分开,说明当压力增大时,只需在适当理论塔板数下,利用精馏工艺能够获得较好的分离效果。
压力对异丙醇与乙二醇二甲醚二元组分气液平衡的影响还可以用异丙醇与乙二醇二甲醚体系的相对挥发度进一步分析。相对挥发度是指溶液中易挥发组分的挥发度与难挥发组分的挥发度之比,用αAB表示,αAB与1.0的偏离程度是精馏操作分离液体混合物难易程度的标志[16-18],相对挥发度的计算式见式(5)。

式中,yA为气相中易挥发组分的摩尔分数;yB为气相中难挥发组分的摩尔分数;xA为液相中易挥发组分的摩尔分数;xB为液相中难挥发组分的摩尔分数。
在异丙醇与乙二醇二甲醚二元组分体系中,异丙醇为易挥发组分,乙二醇二甲醚为难挥发组分,异丙醇对乙二醇二甲醚的相对挥发度αAB可由图1和图2的气液平衡数据通过式(5)计算得到,1.01×105Pa和5.07×105Pa下异丙醇与乙二醇二甲醚体系的相对挥发度αAB计算结果见图3。
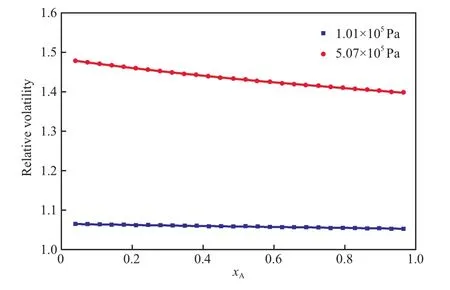
图3 异丙醇与乙二醇二甲醚体系在1.01×105 Pa和5.07×105 Pa条件下的相对挥发度Fig.3 Relative volatilities of the IPA-DMEN system at 1.01×105 Pa and 5.07×105 Pa.
由图3可看出,增加压力使异丙醇与乙二醇二甲醚体系的相对挥发度αAB也增大。1.01×105Pa下的αAB均接近于1.0,进一步说明常压时使用精馏操作不能将异丙醇与乙二醇二甲醚混合溶液分离,当压力为5.07×105Pa时,异丙醇对乙二醇二甲醚的相对挥发度αAB增大,在1.4~1.5的范围内,远远偏离1.0,充分为加压精馏能有效分离异丙醇与乙二醇二甲醚的混合溶液提供了理论依据。
2.3 最小理论塔板数与最小回流比的确定
最小理论塔板数和最小操作回流比的确定是精馏设计过程中的首要任务[19]。对某制药企业的异丙醇与乙二醇二甲醚混合溶液进行分离,其中,异丙醇与乙二醇二甲醚的含量均为50.0%(w),分离要求为:塔顶产品中异丙醇的含量为98.0%(w),塔底产品中乙二醇二甲醚的含量为98.0%(w)。根据图1和图2中5.07×105Pa下的气液平衡数据、进料组成及分离要求,利用Fenske方程计算最小理论塔板数Nm,利用Underwood公式计算最小回流比Rm[19]。在保证分离要求的前提下,操作回流比越大,则所需要的理论塔板数越少。在全回流情况下,完成分离要求所需的理论塔板数为Nm。Nm用Fenske公式进行计算,计算公式见式(6)。


利用式(6)和式(7)计算得到操作压力为5.07×105Pa时分离异丙醇与乙二醇二甲醚混合溶液的最小理论塔板数Nm=27,最小回流比Rm=3.4。
2.4 实际精馏装置的建立及实际分离结果的分析
通常实际精馏装置塔板数取Nm的1.2~2.0倍,操作回流比取Rm的1.2~2.0倍,再结合实际情况建立实际精馏装置。对某企业3 kt/a异丙醇和乙二醇二甲醚混合溶液建设回收装置,得到实际精馏装置的设备参数为:规整填料塔,实际理论塔板数为45块,填料型号为BX型[20],操作压力为5.07×105Pa,Rm=4.0。为了使精馏塔塔顶与塔底均能得到高纯度产品,实际精馏装置建立了严格的操作控制系统。
在实际精馏塔流出股取样分析塔顶与塔底产品,试样的气相色谱分析结果见图4。由图4可知,有效时间为3.553 min的峰对应的物质为异丙醇;有效时间为3.864 min的峰对应的物质为乙二醇二甲醚。
利用气相色谱的面积归一化法进行定量分析,得到塔顶产品中异丙醇的含量为98.9%(w),塔底产品中乙二醇二甲醚的含量为99.5%(w)。实验结果表明,生产装置在实际运行过程中取得了很好的分离效果,塔顶回收的异丙醇含量保持在98.0%(w)以上,塔底回收的乙二醇二甲醚含量高达99.5%(w),满足了制药企业对混合溶媒循环使用的要求。
不同热力学模型模拟结果与实际实验结果见表3。从表3可看出,采用NRTL热力学模型、Wilson模型和UNIQUAC模型模拟的结果都接近于实际生产装置的分离结果;而采用UNIFAC热力学模型模拟的结果与生产装置分离相差显著,这是因为UNIFAC热力学模型计算当操作压力为5.07×105Pa时,异丙醇与乙二醇二甲醚两组分存在共沸组成,与生产装置的分离结果不符,因此,UNIFAC模型不适用于该条件下异丙醇与乙二醇二甲醚混合体系的模拟计算,从而进一步证明了选择NRTL热力学模型研究异丙醇与乙二醇二甲醚混合体系的合理性和准确性。

图4 塔顶(a)和塔底(b)产品的气相色谱图Fig.4 Gas chromatogram of products at the top(a) and bottom(b) of the column.

表3 不同热力学模型模拟结果与实际结果的对比Table 3 Comparison between simulation results of different thermodynamic models and actual results
3 结论
1)随着操作压力的增大,异丙醇与乙二醇二甲醚的沸点差不断增大,为异丙醇与乙二醇二甲醚的分离提供了理论依据,实验适宜的操作压力为5.07×105Pa。
2)1.01×105Pa与 5.07×105Pa下异丙醇与乙二醇二甲醚气液平衡数据表明,加大压力能够有效提高体系的相对挥发度,使异丙醇与乙二醇二甲醚混合溶液容易分离;采用Fenske公式和Underwood公式得到最小理论塔板数Nm=27,最小回流比Rm=3.4。
3)根据研究结果与实际情况建立实际精馏装置,实际精馏塔塔顶回收的异丙醇含量为98.0%(w)以上,塔底回收的乙二醇二甲醚含量为99.5%(w),均满足企业溶媒循环使用的要求。
4)NRTL、Wilson和UNIQUAC模型的模拟结果与实际装置分离结果相近,而UNIFAC模型的计算结果与实际不符,进一步表明选择NRTL热力学模型模拟具有合理性。


