高中数学圆锥曲线的离心率求解方法

周艳群

(广东省珠海市红旗中学 广东 珠海 519000)

离心率是圆锥曲线中的一个重要概念，它的变化将直接影响到圆锥曲线的类型和形状，以离心率作为考察内容的题目在近些年的高考中屡次出现。因此，这部分是当前高中数学教学中的一项重点，不少学生在面对有关问题时都会觉得束手无策。本文将结合近些年出现的各类型试题，具体分析高中数学圆锥曲线的离心率求解方法。

1.基本量法

利用基本量法来求解离心率主要是指通过题目中已知的条件来求得参数a、c之间的关系，从而得到离心率e。

这一类型的解题方式相对来说比较简单，只要能够从题目已知中准确找到a、b、c三个基本量，就可以计算出离心率的值了。

2.定义法

例2 (1)在等腰△ABC中，∠ABC为120°，求以A、B为焦点且过点C的双曲线的离心率.

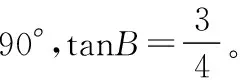
3.向量法

向量知识的应用无疑是拓展了我们的解题思维，在求解离心率的过程中，向量可以更简单的解决含有垂直和共线的题目。

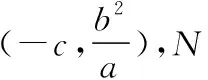
4.参数法

在解决圆锥曲线的离心率问题是，如果题目的已知条件中含有参数，且知道或可以容易求得参数的范围，那么我们就可以通过分析离心率与参数之间的关系来确定离心率的范围。

因为2m+m=3m=2a，所以꿐

5.平面几何图形法

相对于代数计算来说，平面几何图形更加形象直观，在解题过程中结合平面几何图形可以让我们更加清晰的认识到数量之间的关系，从而降低解题难度，提高解题效率。

总之，圆锥曲线中的离心率计算是解析几何中的重点内容，也是近些年高考中最常见的题型。如果学生在学习中没有有效的思维拓展，只是就事论事，忽略了对题目的反思与总结，那么教学的效果必然不会十分明显。数学知识之间通常是有着十分密切的联系的，解题思路也是灵活多变，解题的方法通常也不唯一。学生在解题过程中即使能够一次性找到答案，也应该尽量去做更多的思考，找到最简最优的方式。同时，还要进一步对题目内容和解题过程进行反思，从中总结出更多的解题规律，实现学习能力与解题能力的进一步提升。