算理与算法相融

王健

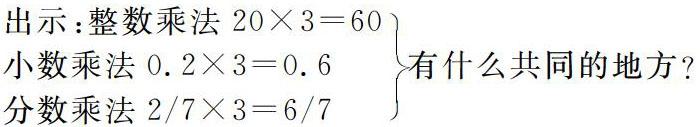
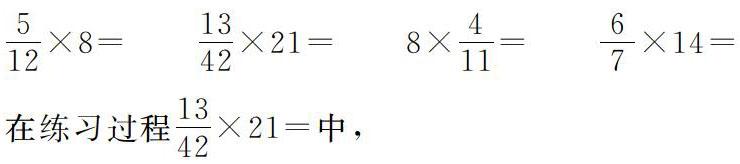
计算教学是小学阶段的重要内容，学好分数乘法对后续学习意义重大。 分数乘整数安排在本单元的第一课时教学，这一内容对沟通学生的知识结构及认知起着承上启下的作用。本人认为，应从以下几个方面来展开教学。

片段一：熟悉情景引入主题

出示例题：小新和爸爸、妈妈一起吃一个蛋糕，每人吃了2/7个，3个人一共吃了几个？

师：谁来读一遍，怎么理解2/7个。生：就是把一个蛋糕平均分成7分，其中的2份就是2/7个。

师：2/7的分数单位是什么？有几个这样的分数单位？

生：（分数单位是1/7）表示2个1/7。

师：会解决吗？生： 2/7×3

师：还可以怎么列算式：生：2/7+2/7+2/7=

师：求几个相同加数的和可以用乘法，也可以用加法。

[思考]人教版的情景有个好处，就是紧扣学生的生活实际，学生很容易入手。同样的本课的主题是小新一家三口吃蛋糕，跟五年级下册的分数加减法情景一脉相承，小新、爸爸和妈妈一家三口一起吃一个蛋糕，每人吃2/7个，3人一共吃了几个？学生很容易提取数学信息和问题。同时也不难找到解决问题的方法。学生可以用加法计算，也可以用乘法来列式计算，学生在观察这两种方法的同时，也能感受到分数乘法与整数乘法意义相同，都是求几个相同加数和的简便计算。

片段二：任务驱动明算理及算法

师：2/7×3=得数是多少？生6/7 。

师：你能用自己说明为什么是6/7？同学们可以在学生材料上来说明你是如何得到6/7？

师：先独立完成 ，再同桌交流。

师：谁来展示一下你是怎么得到6/7的？

生1： 2/7×3=  2×3/7 = 6/7（个）

师：为什么分子乘3就可以了，而分母不变呢？你能结合图说说理由吗？

生1：因为3个两块就是6块，就是6个1/7，就是6/7。

生2： 2/7×3=2/7+2/7+2/7=2+2+2/7= 6/7（个）

生3：我是用线段图来表示的，把一条线段平均分成7份，这样的2份就是2/7，有3个2/7，合在一起就是6/7.

让学生上台对着图说一说自己的想法

2/7×3=  2×3/7 = 6/7（个）

师：不管是圆形图，还是线段图，为什么都可以表示？

生：因为都是2个1/7×3=6个1/7（板书）

回顾方法：我们在实际计算中，这个中间过程可以省略，直接2/7×3= 2×3/7 = 6/7（个）

【思考】在学生找到解决问题的方法之后，2/7×3= 如何计算就是学生面对的问题，大部分学生根据原有的知识及认知会很快的得到结果6/7，学生可能用加法得到，也可能用分子乘整数得到分子，分母不变得到结果，这些都值得肯定，接下来老师布置任务，你是如何得到6/9的，这是一个关键任务，让学生来说明自己如何计算的，老师给大家提供的学习材料中有各种选择，列式说明，也可画图说明，还可自己用其他的方式来说明自己的計算结果。这样学生就有很多种选择来说明自己的思考过程，学生比较容易接受。

片段3：沟通方法促联系

师：观察我们现在学习的分数乘法和以前学习的小数乘法和整数乘法有什么共同的地方？

师：先独立思考  再同桌交流

师：你有什么发现？ 乘法意义相同：都是求几个相同加数的和。

师：出示20×3

师：观察它们有什么相同的地方？

生：都是计算2×3=6的，只是它们的计算单位不一样？

总结：计算方法想通，都是计算有几个这样的计数单位。

【思考】学生对新知的学习是建立在旧知的基础上的，如果能把新知和旧知连成线、结成网，那学生对于知识的建构就更全面，有助于学生对数学学习的充分理解和感悟。在此阶段，让学生联系小数的乘法意义，整数的乘法意义，显然能发现，它们的意义都是相同的，都是求几个相同加数的和。在计算方法的的沟通上，通过观察会发现，它们都是计算有几个这样的分数单位。

片段四、联系提高促巩固

师：。完成以下练习。

在练习过程中，

师：为什么这题很难口算？生：因为分子是13×21是两位数乘两位数，口算比较难。

师：能不能不计算13×21就能知道结果？仔细观察一下分母和整数的特点，它们有什么关系？

生：42是21的倍数，可以先约分是13/2。

【思考】先约分再计算还是计算之后再约分，学生在原来学习的基础上都是先计算在约分的，这是受到了分数加减法的影响。因此，设计了一道口算不能很快得出结果的题。应引导学生仔细观察分母和整数有什么关系，是计算之后约分还是计算之前约分，学生可以有一个明确的对比，显然，先约分在计算比较简便，在分数乘法中，这是一个重要的计算技巧。

分数乘整数的教学是学生感受乘法另一种意义的的重要支撑，求一个数的几分之几是多少，用乘法来计算，通过练习整数乘法的基本原理得出分数乘整数的计算方法，学生比较容易理解，再引导学生把分数乘法转化成分数加法，在此基础上得出计算方法。然后沟通计算方法。这样的教学活动有助对乘法运算意义及方法的整体理解。