少周期强激光脉冲下光电子谱的Fisher信息

班玉英,李岩,赵晓云,李婵,郝小雷*,李卫东

(1.山西大学 理论物理研究所,山西 太原 030006;2.太原师范学院 物理系,山西 晋中 030619)

0 引言

随着超快强激光技术的快速发展,强场物理逐渐向定量化发展,对实验测量精度的要求越来越高,例如对少周期激光脉冲载波包络相位(carrier-envelope phase,CEP)的测量[1-2]。对于超短脉冲,电场E(t)=E0(t)sin(ωt+φCEP)强烈依赖于φCEP(载波包络相位(CEP))。CEP决定了周期量级超短激光脉冲的电场形状，通过CEP的变化可以改变电场最大值在脉冲包络内的位置,这将直接影响阿秒脉冲的产生[3]。根据阿秒计量学和光谱学的需要,单次超短激光脉冲的完整表征需要精确测量电场和脉冲包络线之间的偏移,即CEP[4]。在强激光场范围,周期量级CEP稳定的超短激光脉冲已经成功地应用在阿秒脉冲的产生和分子解离电离动力学的操纵[5-6]。理论和实验证明,精确测量CEP对于充分表征少周期性激光脉冲以及全面理解少周期下场-物质相互作用具有特别重要的意义[7]。当前实验上主要采用2009年Wittmann等人[1]提出的立体阈上电离能谱仪来测量少周期强激光脉冲的CEP。其主要原理是利用光电子发射方向对CEP的敏感依赖,通过测量激光极化轴两个相反方向的能谱来确定CEP,对于某些CEP的测量精度高达π/300。实验上测量CEP的误差一方面来自于对激光脉冲其他参数的表征和控制以及对电子能量测量存在误差,另一方面则来自于物理系统的本征误差,即测量的精度上限。近年来人们通过不断提高激光光强、脉宽等参数的控制精度,不断优化电子能谱测量装置,来实现更高的CEP测量精度[8-9]。但是,对于立体阈上电离能谱仪测量CEP的精度极限还缺乏研究,因此需要相应的理论研究为实验上进一步提高测量精度提供依据。

Fisher信息与精密测量密切相关,可以用来对系统待测参数的精度进行估计[10]。依据Cramer-Rao Lower Bound(CRLB),即克拉美罗下界,Fisher信息越大,精确度越高。另外,Fisher 信息还可用于判定量子纠缠,如用于判定多粒子纠缠的判据,判定κ粒子真正纠缠等[11-13]。

本文我们将通过提取Fisher信息,依据克拉美罗下界表征CEP测量的精确度,在理论上给出不同CEP测量精度的极限。首先，我们通过求解含时薛定谔方程(Time-dependent Schrödinger equation，TDSE)的方法得到氢原子不同CEP下包含左右两个方向的光电子能谱。然后，将其转换为动量谱,再利用Hellinger距离公式提取动量谱中表征CEP精确度的Fisher信息。最后，我们得到了0-2π范围内不同CEP下的Fisher信息值。

1 理论计算

1.1 TDSE模型计算动量谱

本文中用到的强激光场中氢原子的含时薛定谔方程可以写成(本文的计算都采用原子单位,即m=ћ=e=1):

(1)

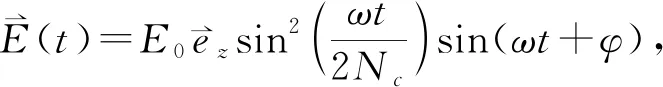
通过“Qprop”的计算我们可以得到左和右两个方向的光电子能谱,然后我们依据公式E=p2/2m,将两方向的能量谱转换为包含左右两个方向所有信息的完整动量谱,并对动量谱的条件概率进行归一化处理,我们将归一后的动量分布作为计算Fisher信息的参数进行下一步计算。

1.2 Hellinger距离提取Fisher信息

在一般的无偏差估计中,Fisher信息可以定义为条件概率的函数,即

(2)

其中p(μ|φ)为给定φ测得μ的条件概率。

提取Fisher信息用到的Hellinger距离公式表示为[15]

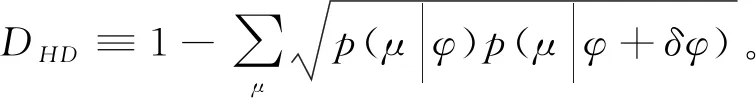
(3)

对上述式子在φ附近进行级数展开可以得到

(4)

其中

(5)

(6)

(7)

图1 氢原子在不同CEP下的光电子能谱图,CEP分别为(a) π/2; (b) π; (c) 3π/2; (d) 2πFig.1 Photoelectron spectroscopy of H atom under different CEPs: (a) π/2; (b) π; (c) 3π/2; (d) 2π

利用Fisher信息表征精确度需要用到的克拉美罗下界(CRLB)的表达式为[16]

(8)

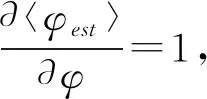
2 数值结果与分析

首先,我们计算了不同CEP的少周期强激光脉冲下氢原子的光电子能谱,如图1(a-d)所示。少周期脉冲的波长为800 nm,光强为8×1013W/cm2。横坐标为光电子能量,纵坐标是对应的电离率,黑色线是左方向的光电子谱,红色线是右方向的光电子谱。从图中可以看出:(1)两个方向的光电子能谱尤其是高能部分有明显的差别;(2)两个方向能谱随CEP有明显的变化,高能部分的拐点和极大值会随着CEP改变而移动,同时两个方向能谱的相对强度也会发生改变,并且CEP相差π时,左右两个方向能谱交换对称(如图1中 (a)与(c),(b)与(d)所示)。

为了能够在同一个分布中同时包含两个方向能谱的信息,我们将能谱转换为动量谱。下面,以CEP为π/2为例,我们依据公式E=p2/2m将光电子能量转换为动量,并把左右两个方向的动量组合,形成完全包含左右两个方向电子信息的动量谱,并将调整后的概率分布做归一化处理,结果如图2所示,其中横坐标是电子动量,纵坐标是对应的电离率。

图2 CEP为π/2的动量谱Fig.2 Momentum spectrum with CEP of π/2

接下来我们将动量谱作为条件概率分布代入公式(3)计算CEP为π/2时的Hellinger距离,其中δφ分别取-π/50,-π/100,0,π/100,π/50计算DHD。然后，将5个数值点做二阶拟合,获取拟合表达式,如图3,横坐标为相位,纵坐标为DHD。从1.2的公式(4)可知,拟合结果二次项系数的8倍即为CEP为π/2时Fisher信息值。

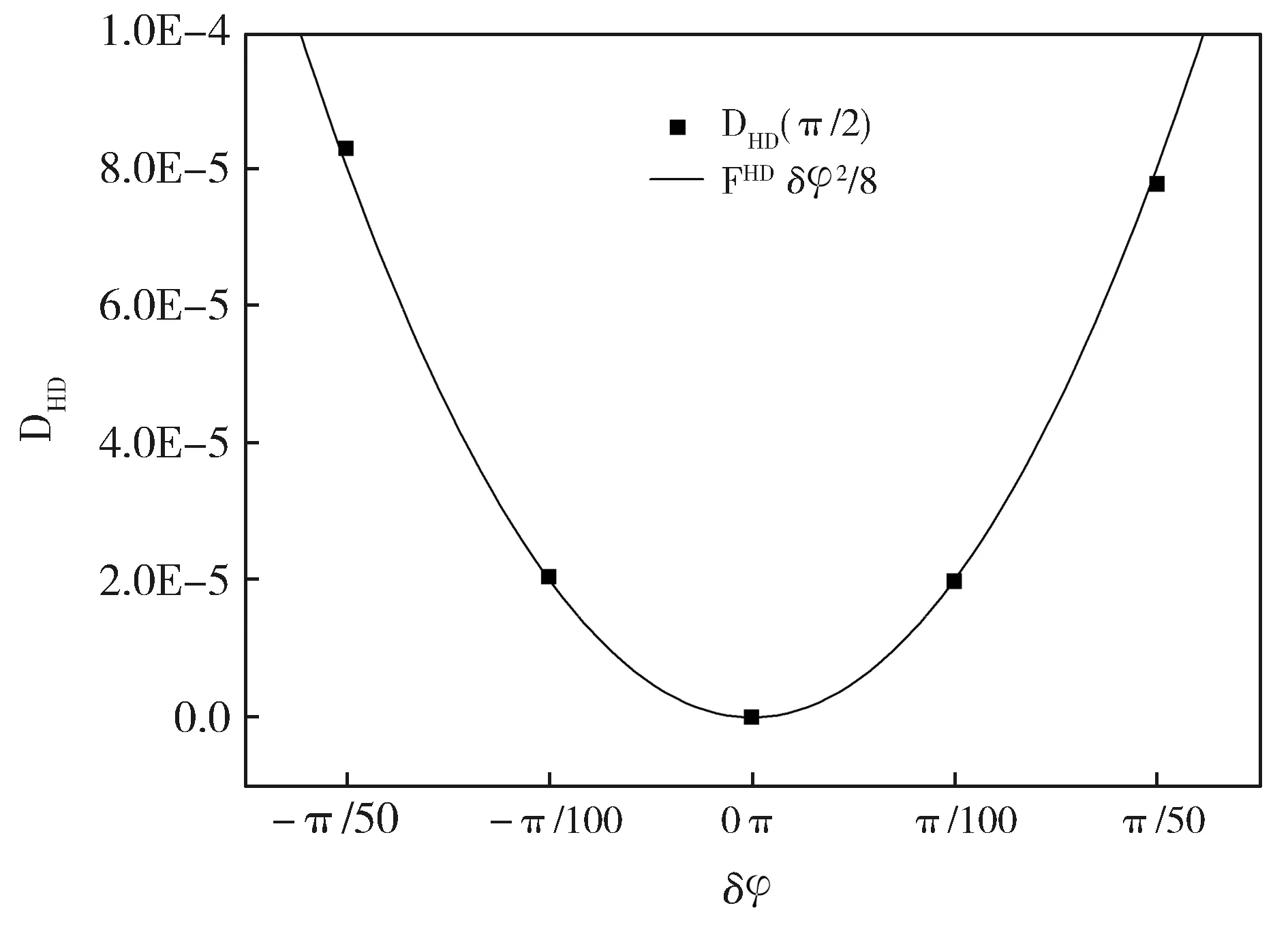
图3 Hellinger距离的二阶拟合Fig.3 Second-order fitting of Hellinger distance

依据上述方法,可以得到0～2π范围内,间隔为π/10的不同CEP下的Fisher信息,如图4,误差棒表示二阶拟合时产生的误差。从图中我们可以看出:(1)在CEP为9π/10和19π/10时Fisher信息值为0.217,达到最大值, 如图中五角星所示,此时的测量精确度最高。(2)Fisher信息值随CEP以π为周期变化。

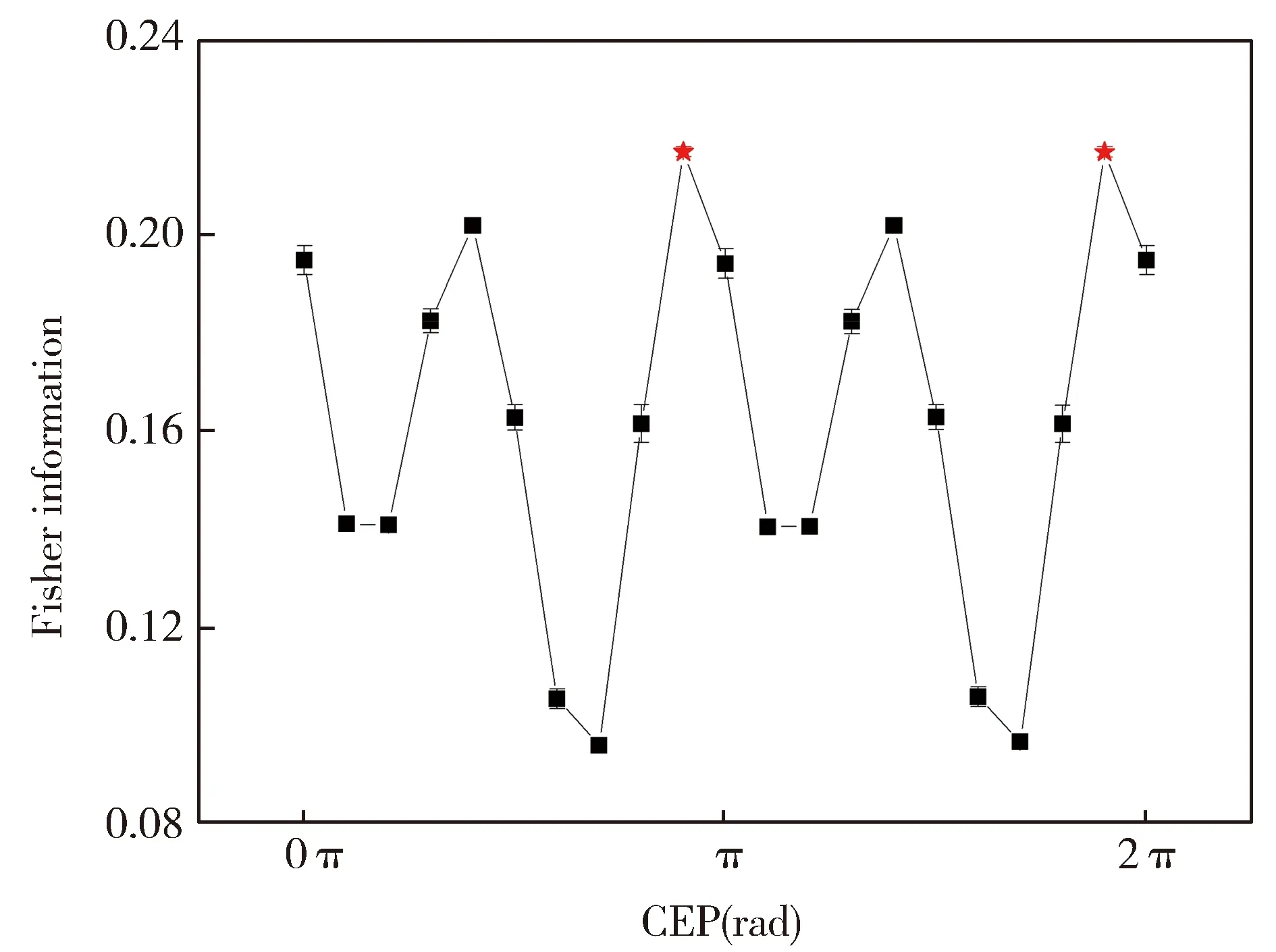
图4 不同CEP下的Fisher信息Fig.4 Fisher information under different CEPs

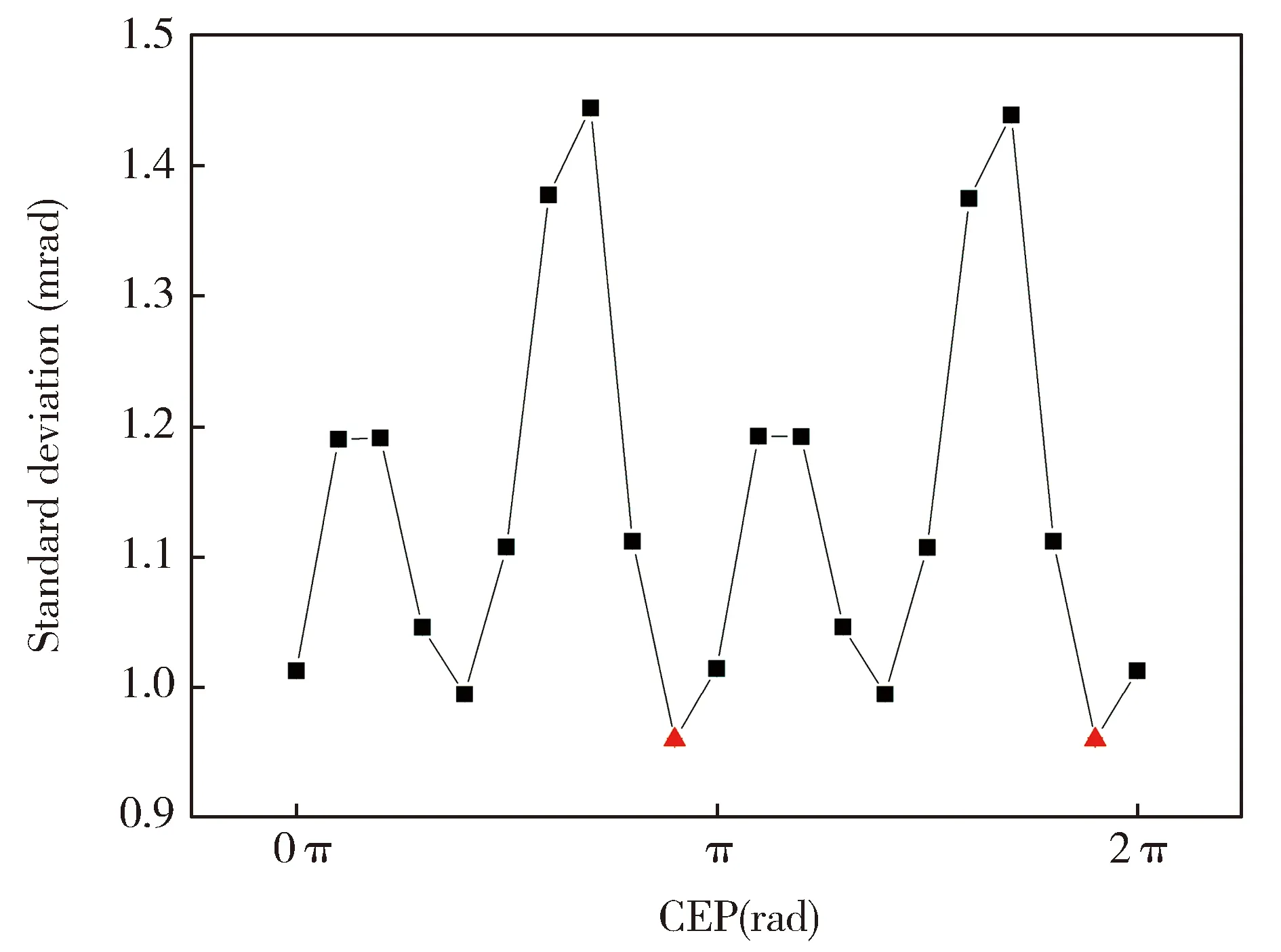
图5 不同CEP下的标准偏差Fig.5 Standard deviation under different CEPs

将图4中的Fisher信息结果带入公式(8)中,得到不同CEP下的标准偏差分布,如图5,横坐标为CEP,纵坐标为标准偏差。公式(8)中的实验次数M我们是依据文献[1]中的实验条件确定的。根据激光焦斑和相互作用腔的压强可以估算出激光焦斑中心位置处的原子个数约为1×105,每一个CEP的测量用到50发激光脉冲,因此每一个CEP的有效实验次数为M=5×106。从图中可以看出:在CEP为9π/10和19π/10时标准偏差最小,如图中三角星所示,约为1 mrad。

到目前为止实验上测量局部CEP的最高精度为10 mrad[1],出现在CEP为5π/9处,远远低于我们理论计算的最高精度。产生差异的原因是实验上每一发脉冲的峰值光强会有一定程度的抖动,同时每一发脉冲的脉宽也不完全相同。而在我们的理论计算中,光强和脉宽都是固定值,因此我们得到的是CEP测量精度的上限。这也表明实验还可以通过对激光参数的精确控制来实现CEP测量精度的进一步提高。

3 结论

本文利用TDSE数值方法,计算了氢原子在800 nm, 8×1013W/cm2的少周期强激光脉冲下不同CEP对应的光电子能谱和动量谱,通过Hellinger距离公式,提取出了对应CEP下的Fisher信息。通过分析发现Fisher信息以及CEP测量精度随CEP以π为周期变化,在CEP为9π/10和19π/10时Fisher信息的值最大,即测量精度最高,可达1 mrad。我们的计算和分析表明利用Fisher信息对超快强场测量实验的测量精度进行表征是可行的。